氧化锌掺钡的电子结构及其铁电性能研究∗

徐佳楠 陈焕铭 潘凤春 林雪玲 马治 陈治鹏

(宁夏大学物理与电子电气工程学院,银川 750021)

1 引 言

纤锌矿(Wurtzite)ZnO是直接带隙半导体材料,其禁带宽度在室温条件下一般为3.37 eV,激子束缚能达到60 meV[1],呈现出优异的磁、光电和光催化等性能,在太阳能电池的制造行业、液晶显示器、光探测器和紫外半导体激光器等方面有着广泛的应用[2−9].尽管其众多的优异特性使得ZnO材料被许多科研人员所关注,但由于ZnO材料本身的光学特性和铁电性较弱而且其本身不具有铁磁性,从而使得ZnO在光学、磁学和铁电领域应用较少.大量研究认为纯的ZnO掺杂不同种类的化学元素能够调控和改善其物理性能:如文献[10]利用湿法氧化的掺杂工艺制备出了由Ag掺杂的ZnO纳米结构,结果显示ZnO掺杂Ag之后的紫外激发强度能够达到纯ZnO紫外激发强度的三倍甚至以上,出现这种结果的原因是因为Ag+光载流子比Zn2+更容易逃逸,所以用Ag掺杂ZnO纳米结构的材料制成发光器的发光效率将会大幅度提高;Lin等[11]采用溶胶-凝胶法制备Li掺杂的氧化锌薄膜在近紫外区发射较弱而在可见光区域发射较强,薄膜含锂量为8%时的饱和磁化强度最大,这主要是因为Li原子掺杂氧化锌能引起锌空位和铁磁性所需的低能隙;Ueda等[12]采用脉冲激光沉积的物理方法成功地制备出了Ni,Mn,Co和Cr掺杂的ZnO薄膜,发现只有Co掺杂的ZnO薄膜在室温下具有铁磁性,而掺入其他三种元素(Ni,Mn,Cr)的ZnO薄膜没有磁性.

最近实验上发现某些元素掺杂可以改善ZnO半导体材料的电子结构,使其呈现出铁电性.Joseph等[13]采用脉冲激光沉积的物理方法,在Si(100)基片上生长出来了Li掺杂的氧化锌体系材料,然后在电容-电压测量中观察到了具有1.2 V存储电压的铁电行为,并且通过观察电容-温度曲线的最大峰值发现铁电相变发生的温度为340 K左右;Onodera等[14]研究了Li掺杂ZnO陶瓷的比热与回线之间的行为并首次观察到ZnO基材料的电滞回线,测量到在室温条件下Zn0.83Li0.17O陶瓷材料的剩余极化强度为0.044µC/cm2,虽然这个数值较小,但是给出了该陶瓷具有铁电性的实验证据;Dhananjay等[15]采用脉冲激光烧蚀技术在Si衬底上生长出了沿c轴取向的Zn1−xLixO(x=0.05—0.15)薄膜,观察到了铁电电滞回线,当Li浓度从0.05增加到0.15时,转变温度(Tc)从290 K增加到330 K,作者认为相对介电值的最大值与Li浓度的Tcis函数有关;Yang等[16]采用直流磁控溅射法在Si(111)基片上制备出了Zn1−xVxO(x=0.005,0.01,0.015等)薄膜,测得的最大剩余极化强度为0.2µC/cm2,因此掺杂ZnO材料的铁电特性逐步引起了关注.

本文以Ba掺杂ZnO半导体体系为研究对象,运用基于密度泛函理论的第一性原理计算方法[17−23]系统地研究了不同Ba原子百分比掺杂对ZnO半导体的电子结构和铁电性能的影响,分析了Ba掺杂原子百分比对ZnO半导体电子性质和铁电性能的影响机理.

2 计算结构和方法

2.1 计算结构

本文采用的晶格模型为理想ZnO在常温和常压下的晶体结构,即六角纤锌矿结构,空间群为P63mc.ZnO晶胞在空间中沿着c轴方向形成六角密堆积结构,其晶格常数实验值[24,25]为:a=b=0.320 nm,c=0.521 nm,c/a=1.600,α=β=90◦,γ=120◦.将一个ZnO原胞分别在x,y和z三个方向进行2×2×1扩展得到包含16个原子的超晶胞(8个Zn原子和8个O原子)作为计算体系.当Ba原子掺入时,计算的ZnO超晶胞中分别有1,2,3,4,5,6,7个 Zn原子被相应数目的Ba原子替代,其结构表示为:Zn1−xBaxO(x=0.125,0.25,0.375,0.5,0.625,0.75,0.875).图1是Zn1−xBaxO(x=0.125)超晶胞的结构示意图,其中红色球体代表“O”原子,绿色球体代表“Ba”原子,浅灰色球体代表“Zn”原子.

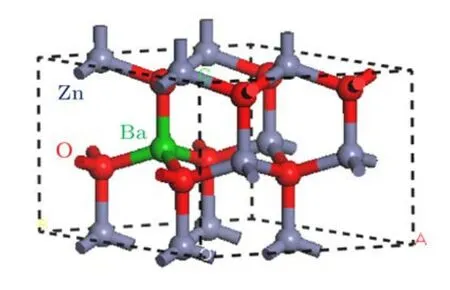
图1 Zn1−xBaxO在x为0.125时的超晶胞结构图Fig.1.Schematic view of Zn0.875Ba0.125O supercell structure.

2.2 计算方法

利用CASTEP软件包分别对ZnO和Zn1−x-BaxO(x=0.125,0.25,0.375,0.5,0.625,0.75,0.875)的超晶胞进行计算和对比分析. 采用Monkhorst-Pack[26,27]方案选取倒空间网格点,电子间的交换相关效应采用局域密度近似LDA-CAPZ泛函[28−33]处理,选取的赝势为模守恒(normconserving)赝势.计算过程中的基本参数设置如下:自洽迭代的收敛精度设定为2×10−6V/atom,作用于每个原子上的力收敛标准设置为0.05 eV/Å,晶体的内应力收敛标准为0.1 GPa,截断能(Ecut)选取为600 eV,倒空间中K点取值为4×4×5.

3 结果与讨论

3.1 结构优化

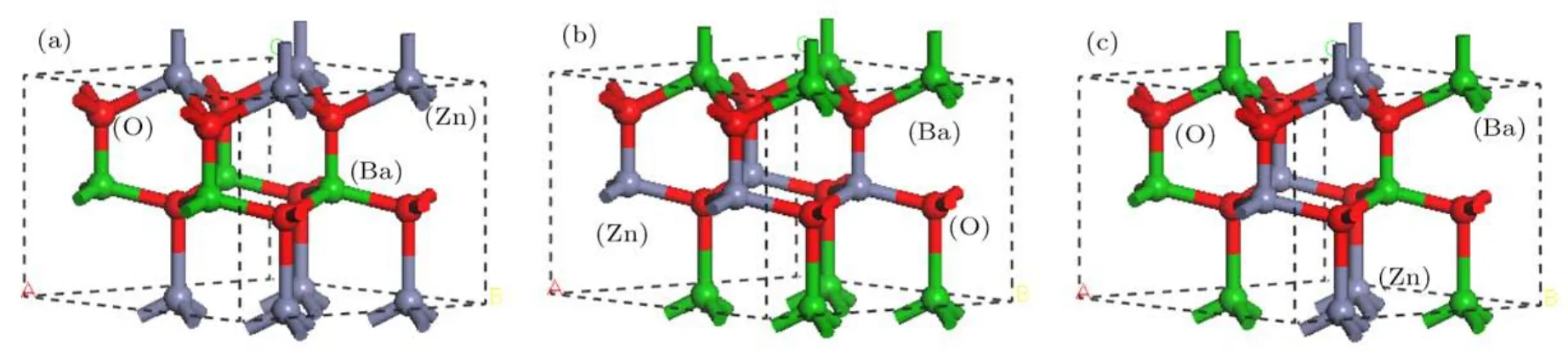
图2 Zn1−xBaxO在x=0.50时不同掺杂构型的超晶胞结构图Fig.2.Supercell structure of Zn0.50Ba0.50O with different doping position.

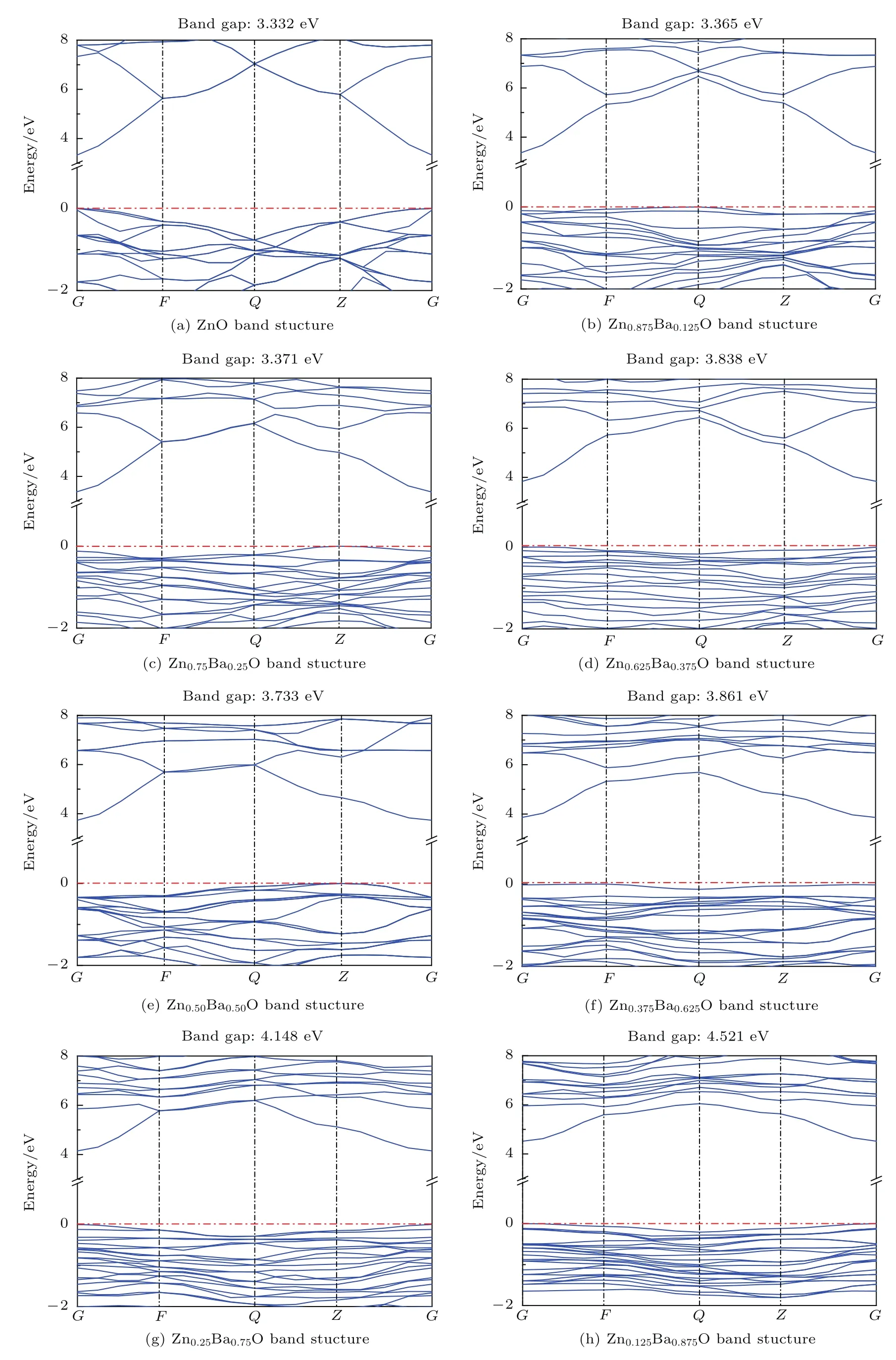
图3 Zn1−xBaxO的能带结构Fig.3.Energy band structures of Zn1−xBaxO.

在计算电子结构和铁电性能之前,为了获得稳定、精确的计算结果,对晶胞结构进行了优化.首先在不同泛函近似下(GGA,LDA和LDA+U)优化了纯ZnO体材料的晶格常数,并计算其带隙值.由表1数据可知:采用GGA和LDA方法计算的带隙值与实验值相差很大,这主要是由于密度泛函理论属于基态理论,无法计算激发态的性质,因而存在带隙计算偏低的缺陷.当采用LDA+U(UZn:3d=10.50 eV,UO:2p=7.00 eV)方法时,计算的ZnO带隙值为3.332 eV,与实验值3.37 eV较为一致,计算值与实验值的相对误差由79.41%(GGA),80.39%(LDA)下降为1.13%(LDA+U),说明处于激发态的ZnO体系是强关联体系,其离子间的相互作用非常强.

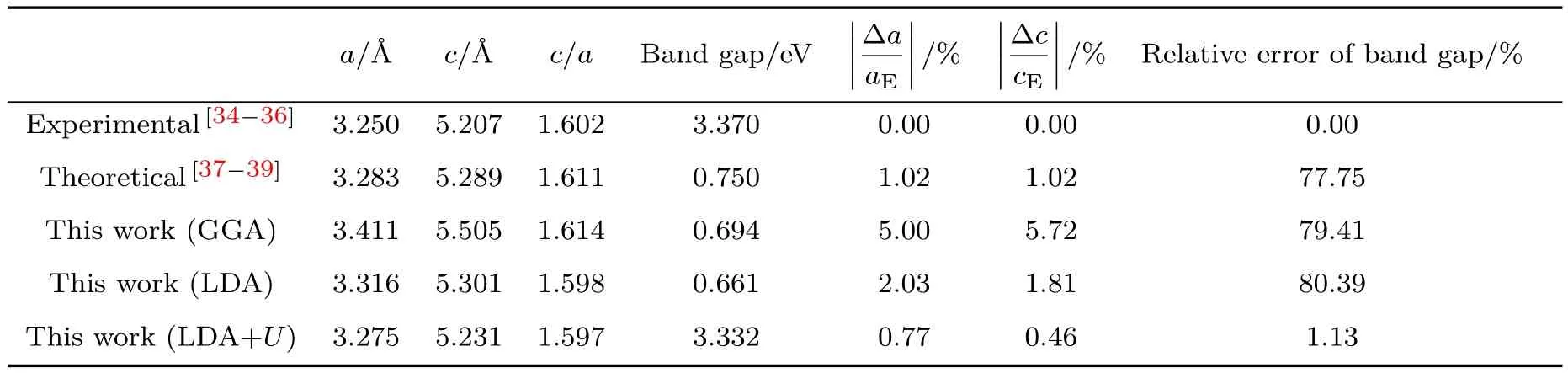
表1 计算结果与实验值及其他理论值的比较Table 1.Comparison of our work with experimental and theoretical values.

另一方面,为了分析同一原子掺杂百分比不同掺杂位置对计算体系稳定性的影响,对同一原子掺杂百分比不同掺杂位置时体系的总能量做了计算. 如这里给出的原子掺杂百分比为50%时的不同掺杂位置时体系的总能分别为−11412.997 eV(图2(a)),−11409.147 eV(图2(b))和−11412.999 eV(图2(c)),表明三种构型体系的总能量相差不大,其中均匀掺杂时(图2(c))体系的总能最低,因此本文采用均匀掺杂的方法进行掺杂体系的性能计算.

3.2 能带结构

Zn1−xBaxO体系属于多原子掺杂体系,掺杂的Ba原子可代替纤锌矿ZnO结构中的Zn原子的多个位置,按照上述结构优化的结果,本文计算与讨论的是1,2,3,4,5,6,7个Ba原子均匀掺杂的情况.图3给出了Zn1−xBaxO体系沿第一布里渊区高对称方向的能带结构图,取费米能级(图中红色虚线)为能量零点,其中图3(a)是纯ZnO的能带图,采用LDA+U方法计算的禁带宽度为3.332 eV,可以看出价带顶和导带底位于同一高对称点G,因此ZnO属于直接带隙半导体[40,41].图3(b)—图3(h)分别是x取0.125,0.25,0.375,0.5,0.625,0.75,0.875时Zn1−xBaxO的能带结构图,计算结果表明:Ba原子掺入后,Zn1−xBaxO的能带结构发生了明显的变化,即随着Ba原子掺杂百分比x的增大,相应的禁带宽度呈增大趋势,特别是x从0.250变为0.375时体系的空间群由Pm变为Cm,禁带宽度的增大更为明显,由x=0.250时的3.371 eV增大为x=0.375时的3.838 eV(图4).Ba均匀掺入ZnO体材料后,由于Ba的金属性比Zn的更强,从而导致O离子的电子密度分布向Ba离子方向的偏移程度比原来为Zn离子时更大,因而O原子和Zn原子间的电子云重叠程度降低进而导致键能下降.另一方面,由于Ba原子的掺入,在价带底部约为−10 eV处出现了新的能带,并且随着Ba原子百分比的增加新能带的宽度逐渐增加(图5(b)—图5(h)),进一步结合3.3节的态密度分析可知这是由Ba原子的p轨道电子所贡献.

图4 Zn1−xBaxO禁带宽度与原子掺杂百分比的关系Fig.4.Dependence of band gap versus dopant percentage.

3.3 电子态密度

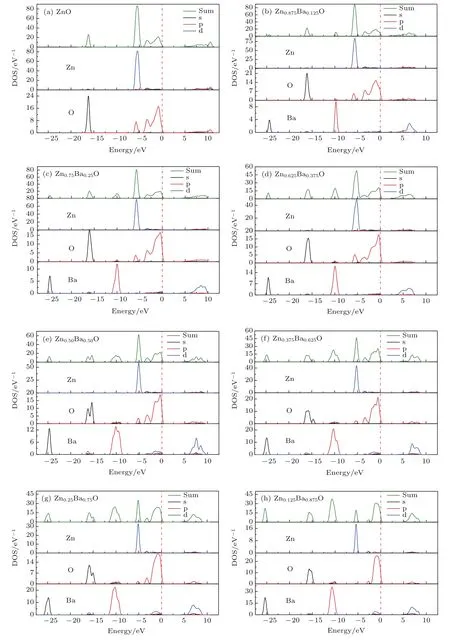
图5 Zn1−xBaxO分态密度图Fig.5.The partial density of states of Zn1−xBaxO.

图5给出了ZnO和Zn1−xBaxO(x=0.125,0.25,0.375,0.5,0.625,0.75,0.875)体系计算的态密度(density of states,DOS)和投影态密度(partial density of states,PDOS),计算过程中Zn1−xBaxO材料的价电子组态分别为:O-2s22p4,Zn-3p63d104s2,Ba-5s25p66s2.由图5(a)可以看出,ZnO的导带主要由Zn的s和p轨道电子以及少量的O的p轨道电子贡献,其价带主要由三部分构成:1)能量位于−17.8—−16.5 eV范围的价带主要由O-2s电子构成,定域性较强,与其他轨道电子间的相互作用很弱;2)能量位于−6.3—−4.0 eV的范围,主要由Zn-3d电子和少部分O-2p电子组成;3)−4.0—0 eV范围的能量处于价带顶,主要由O-2p电子构成.由图5(b)—图5(h)可知,掺入Ba原子后,对价带顶和导带底的态密度而言,与纯ZnO结构相比变化不是很明显,只是在能量为−25 eV和−10 eV附近出现了新的态密度峰,并且随着Ba原子掺杂百分比的增大,峰值不断增高,这是由Ba的p轨道电子所贡献.同时图5也表明:随着Ba原子掺杂百分比的增加,Ba-6s轨道电子与Zn-4s,Zn-4p以及O-2p轨道电子发生了相互作用,使得价带顶O-2p电子的态密度峰向低能区移动,导带底Zn-4s电子的态密度峰向高能区移动,因此随着原子掺杂百分比的增加Zn1−xBaxO体系的禁带宽度变大.

图6给出了纯ZnO与掺杂ZnO在(111)面上的电子密度图,可以看出,Ba离子与周围O离子的电子云交叠程度相对于Zn离子与周围O离子的较大,说明Ba离子与O离子之间存在较强的轨道杂化,Ba—O键的键合作用大于Zn—O键.主要原因是Ba的金属性比Zn的金属性强,导致O离子的电子密度分布向Ba离子的方向偏移程度比原来为Zn离子时的更大,这样Ba离子与其他O离子的相互作用也就大于原来Zn离子与其他O离子的相互作用,不难预知,原子掺杂百分比越大,上述电子密度的变化也越大.

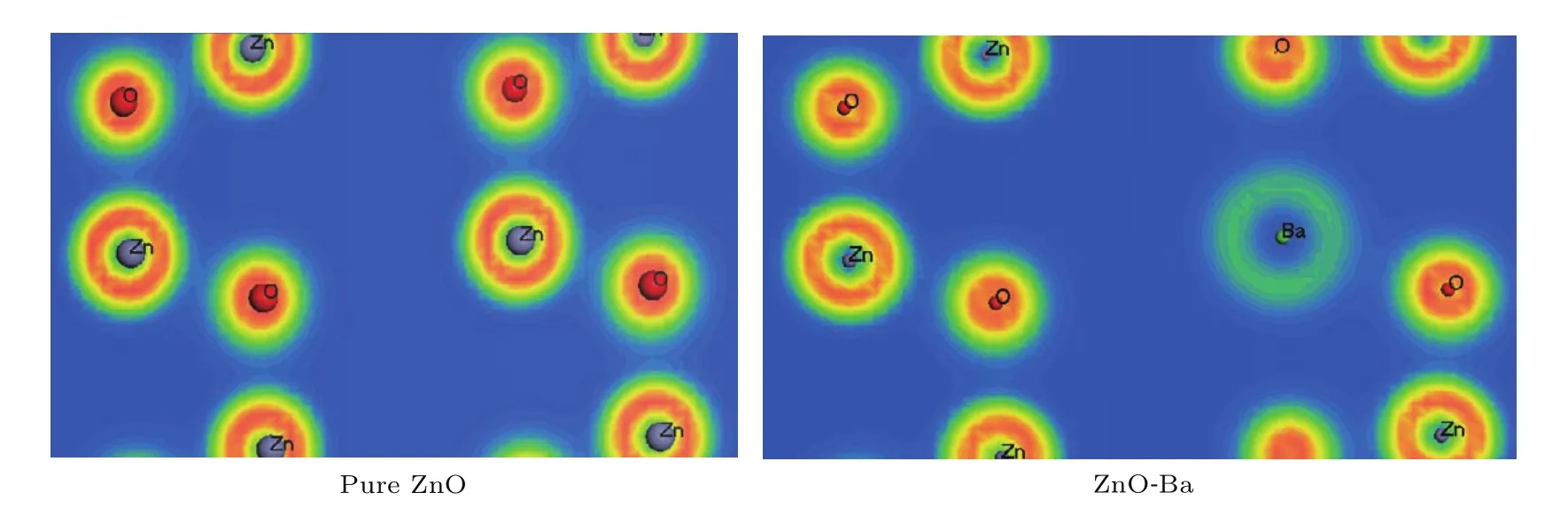
图6 ZnO和Ba-ZnO的电子密度图Fig.6.The electron density graph of ZnO and ZnO-Ba.

3.4 Ba掺杂对ZnO铁电性的影响

纤锌矿结构的ZnO对称性低,Zn与O之间的结合键处于共价键和离子键之间,因此ZnO沿c轴方向具有较强的极性,ZnO沿c轴的极性以及极性面的存在使得ZnO本身具有铁电性.实验证明Ba掺杂ZnO后,材料的光学性能不仅可以得到改善,铁电性能也有很大的变化[42],其铁电性主要来自于晶体的电子位移极化、离子位移极化和固有电偶极矩的转向极化[43,44],并且文献[45]的研究结果表明增加体系的铁电性能够提高太阳能电池器件的光电转换效率.表2给出了不同原子百分比含量的Ba掺杂ZnO后计算所得体系的结构参数,数据表明Ba掺杂ZnO晶体相比未掺杂的纯ZnO晶体而言,其晶格常数发生了明显变化,这一结构的变化导致其极化位移发生改变,从而得到不同掺杂体系的极化率χ和相对介电值εr.

表3给出了不同原子百分比含量的Ba掺杂ZnO后计算所得Zn1−xBaxO体系的极化率与相对介电值.可见,Ba原子替换Zn原子掺入后,由于其相对较大的原子半径(217 pm)使得ZnO纤锌矿结构的原子键长以及Zn1−xBaxO体系的对称性发生改变,进一步使得Zn1−xBaxO体系的极化率与相对介电值发生对应的变化,总的极化率随Ba原子掺杂百分比的增大而呈增大趋势,其中当原子掺杂百分比的含量为75%时,极化率最大、铁电性最强.相反,相对介电值随着原子掺杂百分比的增大呈现减小的趋势,这与Ba原子的分态密度有关.Ba原子掺杂百分比越高,Zn1−xBaxO体系的结构对称性破缺越严重,使得其在外场的作用下更容易极化,这一计算结果与在高频外电场作用下电子位移极化引起的晶体电子极化率与极化强度的单体近似定量关系(1)式一致,这是由于本文计算的Zn1−xBaxO体系是由原胞扩展得到的超晶胞结构,而单体近似定量关系式本身也适用于单胞铁电极化值的等效计算(或者单位超胞体积中超晶胞极化的等效计算):

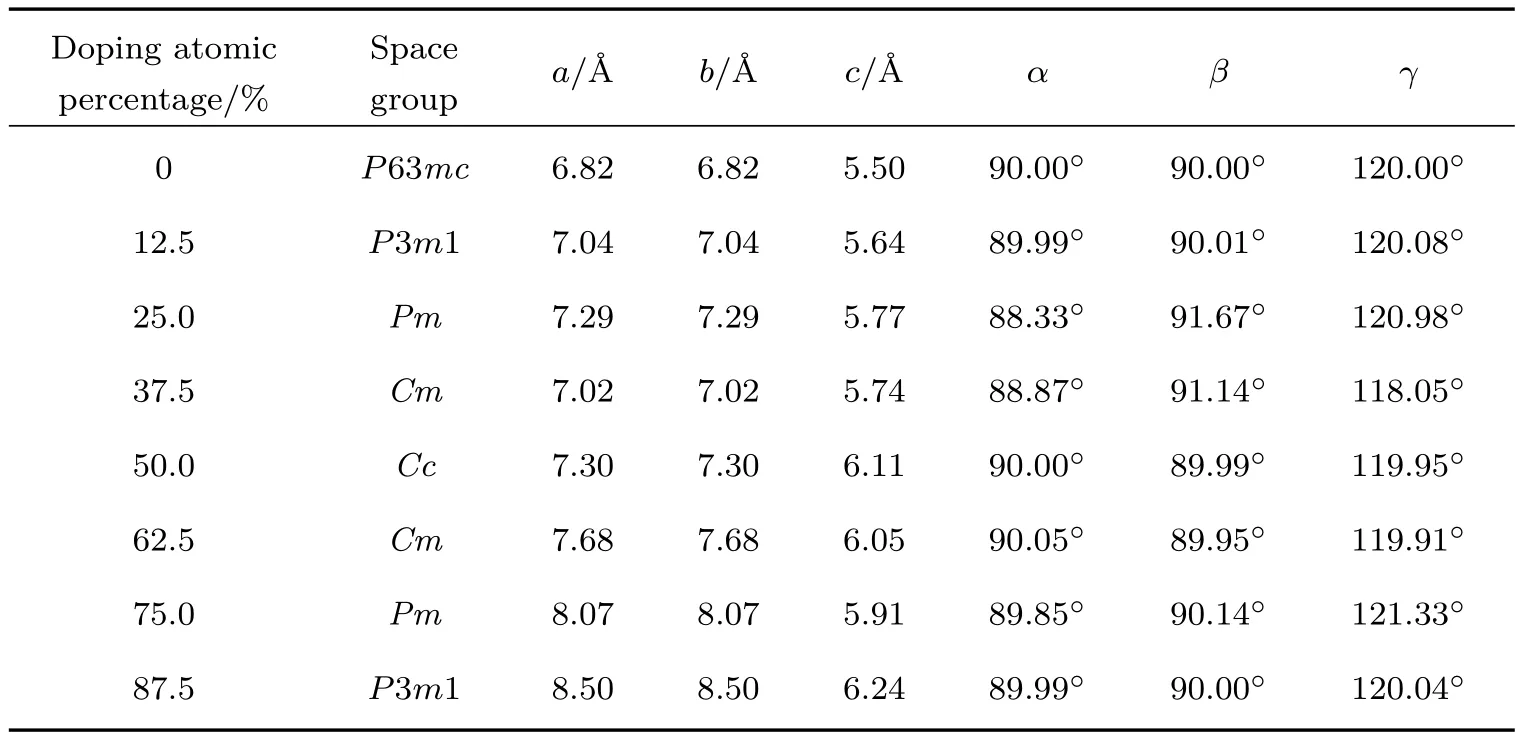
表2 Ba掺杂ZnO体系的结构参数Table 2.Structural parameters of Ba doped ZnO systems.

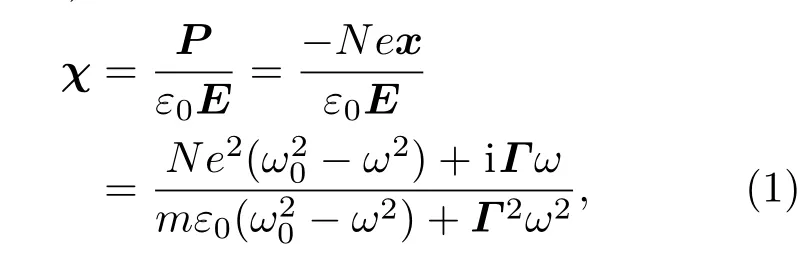
其中χ为介质的极化率,ε0为真空中的介电常数,x为在高频电场作用下电子相对原子核的位移,−ex为每个电子产生的电偶极矩,E为电场强度,N为电子数密度,m为电子质量,ω为频率,ω0为价电子从价带跃至导带所需要的频率,Γ为电子振动过程中的阻尼系数,P为极化强度.另外,从表3中可以看出计算所得的二阶张量极化率对角化后在x,y,z三轴方向上的值相差不大,这与超胞中具有局域的铁电极化有关,即超胞中局域偶极矩集体呈现有序化,预示着在电场作用下超胞中可能存在微畴结构,同时,由于畴间电偶极矩的强相互作用,使得超胞宏观上表现为几乎具有各向同性的极化率特征.

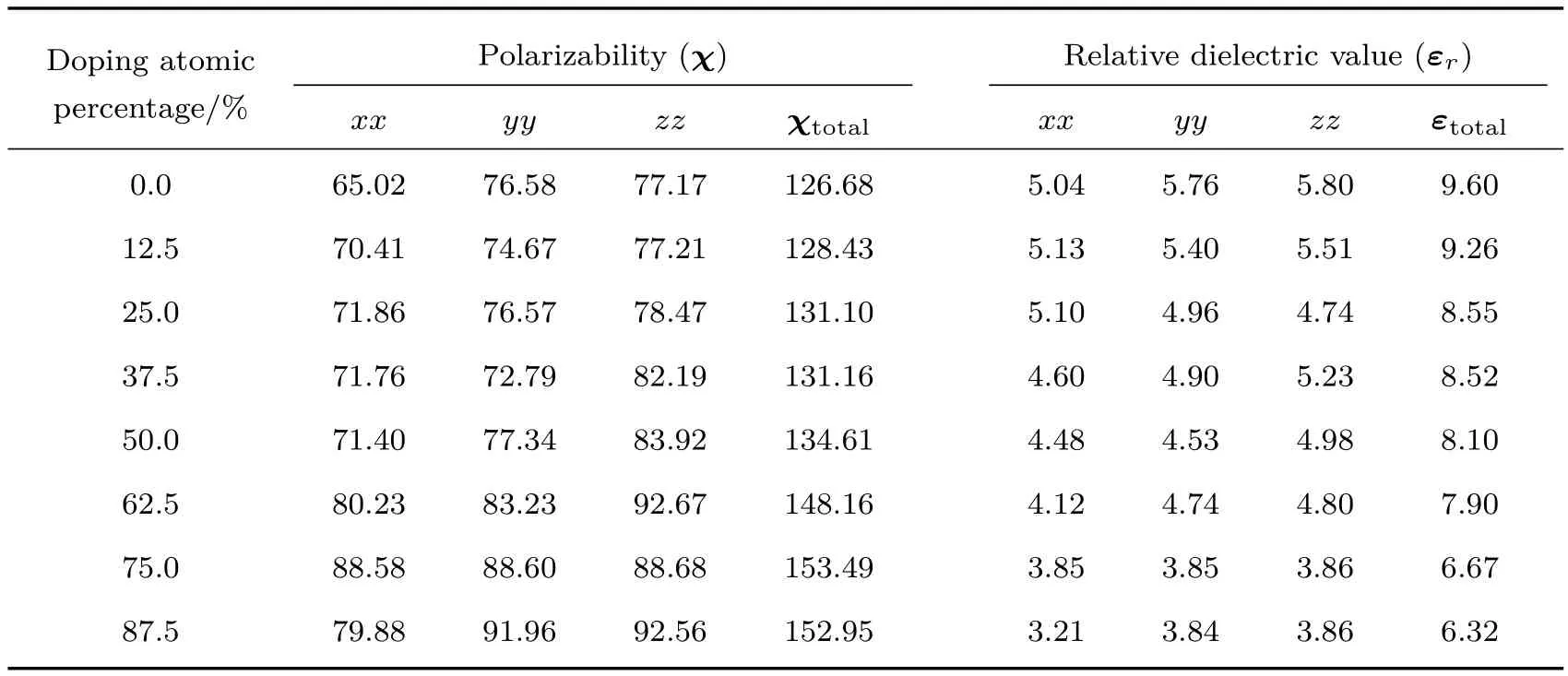
表3 Ba掺杂ZnO体系的极化率和相对介电值Table 3.Polarizability and dielectric constants of Ba doped ZnO systems.

4 结 论

运用基于密度泛函理论的第一性原理计算方法,以Ba掺杂ZnO半导体体系为研究对象,计算了不同原子百分比含量的Ba掺杂对ZnO半导体的电子结构和铁电性能的影响.结论如下:1)Ba替换Zn原子位置可以有效增加ZnO体系的禁带宽度,随着掺杂浓度的增大,Zn1−xBaxO体系的禁带宽度相应增大;2)Ba掺杂纤锌矿ZnO体系的铁电极化性能、介电性能与Ba原子的原子百分比含量有关,Zn1−xBaxO体系的极化率随着原子掺杂百分比的增大呈增加趋势,当掺杂原子百分比为75%时,极化率最大;相对介电值随着原子掺杂百分比的增大呈现减小的趋势,这一结果与在价带底部能量约为−10 eV处Ba原子对体系态密度的有效贡献有关;3)7种不同原子百分比掺杂后所计算的极化率二阶张量的对角化结果均显示在电场作用下超胞中可能存在有微畴结构,并且由于畴间电偶极矩的强相互作用,使得超胞宏观上表现为几乎具有各向同性的极化率特征.

[1]Kim K J,Park Y R 2001Appl.Phys.Lett.78 475

[2]Bagnall D M,Chen Y F,Zhu Z,Yao T,Koyama S,Shen M Y,Goto T 1997Appl.Phys.Lett.70 2230

[3]Aoki T,Hatanaka Y,Look D C 2000Appl.Phys.Lett.76 3257

[4]Shen W F,Zhao Y,Zhang C B 2005Thin Solid Films483 382

[5]Yamamoto N,Makino H,Osone S,Ujihara A,Ito T,Hokari T,Maruyama T,Yamamoto T 2012Thin Solid Films520 4131

[6]Hu Q C,Ding K 2017Chin.Phys.B26 068104

[7]Que M L,Wang X D,Peng Y Y,Pan C F 2017Chin.Phys.B26 067301

[8]Lu Y J,Shi Z F,Shan C X,Shen D Z 2017Chin.Phys.B26 047703

[9]Gao H X,Hu R,Yang Y T 2012Chin.Phy.Lett.29 017305

[10]Chen R Q,Zou C W,Bian J M,Adarsh S,Gao W 2011Nanotechnology22 105706

[11]Lin Y H,Ying M,Li M,Wang X,Nan C W 2007Appl.Phys.Lett.22 197203

[12]Ueda K,Tabata H,Kawai T 2001Appl.Phys.Lett.79 988

[13]Joseph M,Tabata H,Kawai T 1999Appl.Phys.Lett.74 1617

[14]Onodera A,Tamaki A,Kawamura Y,Sawada T,Yamashita1 H 1996J.Appl.Phys.35 5160

[15]Dhananjay,Nagaraju J,Krupanidhi S B 2006J.Appl.Phys.99 034105

[16]Yang Y C,Song C,Wang X H,Zeng F,Pan F,Xu N N,Li G P,Lin Q L,Liu H,Bao L M 2008Appl.Phys.Lett.92 10715

[17]Dang H L,Wang C Y,Yu T 2007Acta Phys.Sin.56 2838(in Chinese)[党宏丽,王崇愚,于涛 2007物理学报56 2838]

[18]Chen Z P,Ma Y N,Lin X L,Pan F C,Xi L Y,Ma Z,Zheng F,Wang Y Q,Chen H M 2017Acta Phys.Sin.66 196101(in Chinese)[陈治鹏,马亚楠,林雪玲,潘凤春,席丽莹,马治,郑富,汪燕青,陈焕铭2017物理学报66 196101]

[19]Chang Y T,Sun Q L,Long Y,Wang M W 2014Chin.Phys.Lett.31 127501

[20]Xu N N,Li G P,Lin Q L,Liu H,Bao L M 2016Chin.Phys.B25 116103

[21]Wang Y P,Wang Y P,Shi L B 2015Chin.Phys.Lett.32 016102

[22]Guan L,Tan F X,Jia G Q,Shen G M,Liu B T,Li X 2016Chin.Phys.Lett.33 087501

[23]Wang H Y,Hu Q K,Yang W P,Li X S 2016Acta Phys.Sin.65 077101(in Chinese)[王海燕,胡前库,杨文明,李旭升2016物理学报65 077101]

[24]Gopal P,Spaldin N A 2006J.Electron.Mater.35 538

[25]Wang X H,Zhang J,Zhu Z,Zhu J Z 2006Colloids Surf.A276 59

[26]Zhao J,Yang X Q,Yang Y,Huang Y H,Zhang Y 2010Mater.Lett.64 569

[27]He X H,Yang H,Chen Z W,Liao S S Y 2012Physica B407 2895

[28]Perdew J P,Chevary J A,Vosko S H,Jackson K A,Pederson M R,Singh D J 1992Phys.Rev.B46 6671

[29]Cao D,Liu B,Yu H L,Hu W Y,Cai M Q 2013Eur.Phys.J.B86 504

[30]Perdew J P,Burke K,Ernzerhof M 1996Phys.Rev.Lett.77 3865

[31]Cao D,Liu B,Yu H L,Hu W Y,Cai M Q 2015Eur.Phys.J.B86 75

[32]Wu L J,Zhao Y Q,Chen C W,Wang L Z,Liu B,Cai M Q 2016Chin.Phys.B25 107202

[33]Liu B,Wu L J,Zhao Y Q,Wang L Z,Cai M Q 2016J.Magn.Magn.Mater.420 218

[34]Delley B 2000J.Chem.Phys.113 7756

[35]Delley B 1990J.Chem.Phys.92 508

[36]Desgreniers S 1998Phys.Rev.B58 14102

[37]Clark S J,Segall M D,Pickard C J,Hasnip P J,Probert M I,Refeson K 2005Z.Kristallogr.B220 567

[38]Erhart P,Albe K,Klein A 2006Phys.Rev.B73 205203

[39]Wimmer E,Krakauer H,Weinert M,Freeman A 2006Phys.Rev.B24 864

[40]Wu Y X,Zhang H,Han L 1996J.Atom.Mole.Phys.28 749

[41]Osunch K,Lombardi E B,Gebiki W 2006Phys.Rev.73 075202

[42]Srinet G,Kumar R,Sajal V 2014Mater Lett126 274

[43]Frost J M,Butler K T,Brivio F,Hendon C H,Schilfgaarde M V,Walsh A 2014Nano Lett.14 2584

[44]Fan Z,Xiao J X,Sun K,Chen L,Hu Y T,Ouyang J Y,Ong K P,Zeng K Y,Wang J 2015J.Phys.Chem.Lett.6 1155

[45]Zhao Y Q,Liu B,Yu Z L,Ma J M,Wan Q,He P B,Cai M Q 2017J.Mater.Chem.C5 5356