采用量子含时波包方法研究H/D+Li2→ LiH/LiD+Li反应∗

李文涛于文涛3)姚明海

1)(渤海大学基础教研部,锦州 121000)

2)(中国科学院大连化学物理研究所,分子反应动力学国家重点实验室,大连 116023)

3)(东风县第三中学,辽源 136300)

1 引 言

近数十年来,计算机科学与数值方法取得的重大进展使得人们可以用量子的方法对复杂的三原子反应、多原子碰撞反应以及三原子三体重组反应等[1−4]进行精确的理论模拟研究.HLi2体系作为一个典型的且具有深势阱的复杂放热反应,在以往的理论研究中常采用近似的方法对其进行理论研究.计算机科学和数值方法的进展使得对HLi2体系进行精确的理论计算成为可能.此外,由于HLi2体系是含有最少电子的最小混合团簇体系并且也是最稳定的中性三聚物之一,这些性质使得HLi2成为研究金属的化学吸附现象和改变合金性质的最佳体系之一.这些特性也使得HLi2体系在实验和理论上都得到了广泛的研究[5−17].

实验上,Wu和Ihle[5]通过质谱测量液体锂中稀释的氢溶液证明了HLi2分子的稳定存在并报道了HLi2分子的离解能(89.7±5.0)kcal/mol.基于一个优化的势能面,Kim和Herschbach[6]更正了势能深度的最小值为(87.9±3.0)kcal/mol.1993年,Vezin等[7]报道了HLi2分子实验光学光谱,并通过模拟第一振动带的转动结构得到了HLi2分子基态与B激发态的几何结构.为了解反应机理,进行动力学散射计算的理论模拟是十分必要的.而势能面是动力学理论计算的基石,因此在过去的几十年中也有大量的理论工作集中在该体系的势能面构建上.

采用自洽场波函和全组态相互作用方法并结合一个收缩高斯基组(H(5s1p/3s1p),Li(8s3p/4s3p)),Siegbahn和Schaefer[8]在1975年构建了第一个HLi2分子体系的势能面.然而计算中采用的基组过小,使得其构建的势能面有很大的改善空间.1997年,Yan等[9]使用285个从头算能量点构建了一个新的势能面.在他们的工作中,采用多参考组态相互作用单双激发方法和6-311G(2df,2pd)基组进行了从头算计算并确定了HLi2分子体系的放热能为32.85 kcal/mol.2010年,Maniero等[10]对394个从头算能量点进行八阶的多项式拟合,从而构建了一个新的势能面.通过对势能面的地形特征分析表明,H+Li2反应是一个没有阈值的放热反应,放热能量约为34 kcal/mol.采用双重多体展开公式对3726个从头算能量点进行拟合,Song等[11]构建了一个HLi2分子体系基态的全维势能面.在计算过程中,采用多参考组态相互作用方法,对于Li原子采用cc-pV5Z基组,对于H原子采用aug-cc-pV5Z基组进行了从头算计算.与Maniero等得到结论类似,明确H+Li2反应是一个放热反应并且放热能为33.668 kcal/mol.最新的势能面是2017年Yuan等[12]采用置换不变多项式神经网络方法对大约30000个从头算能量点进行拟合得到的.在他们的工作中,采用MRCI-F12方法结合aug-cc-pVTZ基组进行了从头算计算.由于H+Li2反应是一个没有阈值的放热反应,因此长程相互作用势可能会对低能的反应碰撞产生大的影响.该势能面采用比较密集的从头算能量点在反应渐进区,以便于得到比较准确的长程相互作用势.

在动力学方面,准经典轨线方法(QCT)和量子方法(QM)经常被用来进行动力学计算.Kim等[13]采用QCT方法分别计算了平动能为0.5,2和10 kcal/mol时H+Li2反应的积分截面.2011年,Vila等[14]采用非含时的量ABC程序在总角动量J=0时对H+Li2→LiH+Li反应进行了动力学模拟,采用J-shifting方法对于J>0进行了计算.理论模拟结果表明,反应物的振转激发对反应起阻碍作用.此外,在0—4000 K的温度范围内计算了H+Li2反应体系的速率常数.2014年,Cunha等[15]采用QCT方法研究了H+Li2体系的同位素效应并报道了平动能范围在0—9 kcal/mol范围内H/D/Mu+Li2反应的积分截面.2015年,Gao等[16]采用含时量子波包方法和二阶分裂算符进行了H+Li2体系的动力学计算,在0—0.4 eV的碰撞能范围内报道了该体系的反应概率和积分截面.此外,他们还发现Li2分子的振动激发在低碰撞能范围内阻碍反应的进行.2016年,为了明确科里奥利耦合在反应过程的重要性,Gao等[17]重新对该体系进行了动力学计算,结果表明科里奥利耦合在反应过程中起着重要的作用.然而,该体系是一个具有深势阱的反应体系,要得到收敛的结果比较耗时.因此,他们在计算中截断了总角动量在体固定坐标轴上投影的数目(k=1[16]和k=6[17]).

综上所述,对H+Li2反应体系已有充分的理论研究.然而,由于该体系是一个高放热并且在反应路径上具有一个深势阱的体系,要得到收敛的结果比较耗时,因此以往的理论研究中往往采用QCT方法或者近似的量子方法.此外,同位素效应是在不对体系进行大的改变的基础上进一步探究反应机理的重要手段,在物理化学、原子与分子物理领域已有同位素对比的广泛研究[18−22].而对于H+Li2反应体系,到目前为止尚未见在量子理论水平进行同位素对比的研究.本文的目标主要集中在两个方面:1)以往的理论研究中对总角动量在体固定坐标轴上投影(k-block)的数目进行了截断,而与科里奥利耦合相关的反应概率、积分截面等动力学性质显著地依赖于k-block的数目,尤其是总角动量J比较大时;收敛的动力学结果有助于理解动力学反应机理,本文进行包含所有k-block数目的动力学计算并与之前的理论研究进行对比;2)将H原子取代为较重的D原子,在量子水平上进行同位素变换的研究,进一步研究动力学反应机理.

2 动力学计算方法

量子含时波包量子方法在动力学计算中已广泛使用[23,24],本文只做一些简单的介绍,详细的信息可以参考文献[25—28].对于给定的总角动量J,H+Li2反应体系的哈密顿量在体坐标系下可以写为

其中G(R)是高斯波包,ϕv0j0是Li2分子的振转方程,(M,j0,l0)是体坐标下体系的初始振转态,ε是体系的宇称.在传播过程中,采用快速傅里叶变换方法[29]进行径向动能算符的计算,采用离散表象变换方法[30]进行势能算符的计算,并采用二阶分裂算符传播构建好的指定初始态的量子波包.为了避免波包在边界处反弹造成二次传播,在计算中采用如下形式的吸收势:

其中Ca,Cb是吸收势的强度;∆t是时间步长;ra,rb,rend是吸收势对应的位置.

通过取代旋量表示下的散射矩阵可以得到态分辨的积分截面

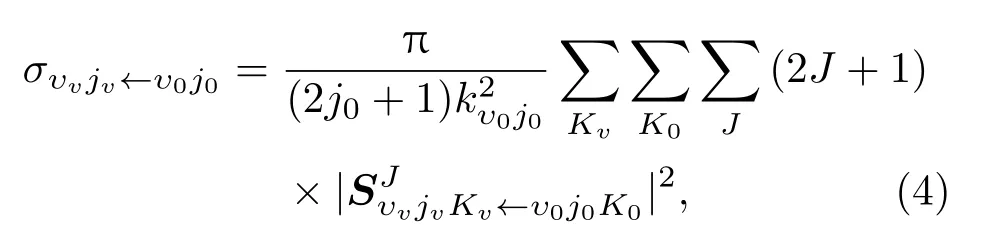
和态分辨的微分截面

其中是散射矩阵,dΩ是方位角,ϑ是散射角,是魏格纳转动矩阵.

3 结果与讨论

在计算中采用Song等[11]报道的势能面,该势能面的主要特征如图1所示.由图1可知,H+Li2反应是一个放热反应,其放热能约为1.46 eV(考虑零点能),并且在反应路径上有一个深势阱,相对于反应物渐进区,其深度约为2.6 eV.

3.1 反应概率

对于H+Li2反应,在总角动量J=0—60的范围内进行了动力学计算.对于其同位素D+Li2反应,计算的总角动量范围为0—70.为了得到收敛的动力学结果,在总角动量J=0时,本文进行了大量的动力学参数测试.得到的最优参数列于表1.对于所有总角动量J>0的情况,采用相同的计算参数.此外,在计算中本文考虑了与k-block密切相关的科里奥利耦合效应.在计算中对于每一个总角动量J,采用的k-block数目为(J+1)和100之间的最小值,这样可以保证总角动量所有的投影都包含在计算中,以便得到收敛的结果.

图1 H+Li2反应5◦—180◦的最小反应能量路径Fig.1. The minimum energy reaction path from 5◦–180◦ for H+Li2reaction.

图2 在0—0.4 eV的碰撞能范围内,H+Li2反应总角动量J=0,10,20,30,40,50的反应概率以及文献[14,17]的结果Fig.2.The total reaction probabilities for the total angular momentum J=0,10,20,30,40,50 of the H+Li2reaction in the collision energy range from 0–0.4 eV as well as the results from Ref.[14,17].

总角动量J=0,10,20,30,40,50的反应概率见图2.如图2所示,在J=0的反应概率上没有阈值出现并且在研究的碰撞能范围内有一些共振峰,这些共振峰的产生是因为在反应路径上有一个能产生大量束缚态和准束缚态的深势阱;伴随着碰撞能的增加,共振峰的强度变弱,共振峰之间的间距变宽.这表明随着碰撞能的增加,碰撞络合物的寿命开始变短.当总角动量J变大以后,反应阈值开始出现并且随着J的增大而增大.反应阈值的出现是因为离心势的变大,离心势随着J的增大而变大.

为了与之前的理论结果进行比较,图2同时给出了文献[14]和文献[17]报道的理论结果.如图2所示,对于J=0,本文结果与文献[17]的结果符合得很好,与文献[14]在低能部分符合得比较好,但是对于高能部分则有较大的差距.这可能是因为在计算中采用不同势能面造成的:文献[14]采用Maniero等[10]构建的势能面仅包含394个从头算能量点,并且采用的基组也有进一步提升的空间;而文献[17]采用Song等[11]构建的势能面从头算能量点的数目几乎是Maniero等[10]的10倍,此外,势阱的深度也比Maniero等[10]构建的势能面更深(1 kcal/mol)也更加接近实验值.势能面的地形结构往往会对动力学结果产生较大的影响.在低碰撞能时,由于平动能低,势阱深度的微弱差距对中间络合物的寿命产生的影响相对较小,所以在低能时,反应概率符合得比较好.当平动能增加时,势阱深度的差异会对中间络合物的寿命产生较大的影响,所以在图2中不难看出随着碰撞能的增加,文献[14]的反应概率与本文反应概率的差距在逐渐变大.

对于J>0,本文的结果与文献[17]的结果有较大的差距,有时甚至不能得到相同的阈值.分析认为,随着碰撞能和离心势的增加,反应概率会逐渐变小.这是一个典型的放热反应特征.因为随着能量的变大,H原子或D原子的速度逐渐变快,以致于Li2分子来不及与快速运动的H原子或者D原子形成HLi键或者DLi键,从而降低反应概率.而文献[17]的结果明显有悖于这样的趋势.例如,J=10的反应概率小于J=20的反应概率,这明显是不合理的.此外,本文结果与文献[17]结果的差距也随着碰撞能的增加变得越来越明显.分析认为,这样的结果或许是因为文献[17]为了节省计算量对k-block数目进行了截断(k=6).在文献[17]中,Gao等[17]对J=30,50时分别对k=1—10,15进行了测试,发现k=6的结果与k=15的结果比较接近,从而认为k=6对于多数J应该是收敛的,并将k=6应用到所有J的计算当中.分析认为这样的做法是值得商榷的,因为k=15无论是对J=30或J=50得到的结果都不是真正意义上的收敛结果.如果k=15得到的结果是不收敛的,那么文献[17]进行的比较将变得没有意义.因此本文以J=30为例对k=1,5,10,15,20,25的结果进行了计算和比较,结果如图3所示.

从图3中不难看出,当k=15时,得到的结果是不收敛的.从图3(b)可以看出,反应概率在高碰撞能范围的巨大差距主要是因为文献[17]没有把所有的k-block值考虑在计算中.

为了解同位素效应的影响,图4给出了碰撞能0—0.4 eV的范围内J=0,60和70的反应概率.由图4可知,当H原子被D原子取代之后,反应概率得到了提升,这或许是因为DLi键的键能弱于HLi键的键能,DLi键比HLi键更加容易形成与断裂.图4还表明,要获得收敛的积分截面和微分截面需要大量的分波计算.本文对于H+Li2反应的最大总角动量J=60,表明当碰撞能低于0.23 eV时.获得的积分截面和微分截面是收敛的.对于D+Li2反应,由于H原子被D原子取代,导致离心势变小.本文计算的最大总角动量J=70在碰撞能低于0.15 eV时,获得的动力学结果是收敛的.

图3 当总角动量J=30时,不同k-block值的反应概率(a)和文献[17]结果的比较(b)Fig.3.The reaction probabilities of the different k-block values(a)and compared with the values obtained from Ref.[17](b).

图4 H/D+Li2反应在总角动量J=0,60和70时的反应概率Fig.4.The total reaction probabilities of the H/D+Li2reaction as the total angular momentum J=0,60,and 70,respectively.

3.2 积分截面与微分截面

如图5所示,H/D+Li2反应的积分截面在0—0.2 eV的范围内随着碰撞能的增加而逐渐降低,这是一个典型的放热反应特征.由图5可知,同位素取代增大了反应的积分截面,尤其是在低碰撞能的时候.这是可以预料的,因为同位素取代也导致了反应概率的增加.

图5 H/D+Li2反应在碰撞能0—0.2 eV范围内的积分截面Fig.5.The total integral cross sections of H/D+Li2 reaction in the collision energy range from 0 to 0.2 eV.

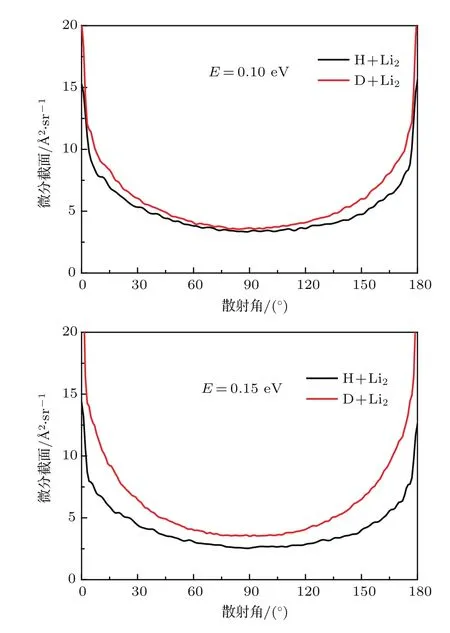
图6 H/D+Li2反应在0.1和0.15 eV时的微分截面Fig.6. The differential cross sections of H/D+Li2 reaction at 0.1 and 0.15 eV,respectively.

当碰撞能为0.1和0.15 eV时,H/D+Li2反应体系的微分截面如图6所示.可见同位素取代同样导致了微分截面的增加,但并未对反应机理产生影响.无论是在0.1 eV还是在0.15 eV时,微分截面都是前后对称的,这表明在整个反应过程中插入反应机理占据主导地位.

4 结 论

采用含时量子波包方法对H/D+Li2反应体系进行了动力学计算,计算过程中考虑了科里奥利耦合效应,报道了体系的反应概率、积分截面、微分截面并考虑了同位素效应.与之前报道的理论结果的比较表明,科里奥利耦合效应在反应过程中扮演重要的角色.由于本文考虑了总角动量J在体固定坐标轴的所有投影,所以本文的结果更加准确、合理.当H原子被相对较重的D原子取代以后,体系的反应概率、积分截面、微分截面均增加了.然而同位素效应并未对反应机理产生影响.从微分截面的结果可知,在整个反应过程中插入反应机理在反应过程中占据主导地位.

[1]Chu T S,Zhang Y,Han K L 2006Int.Rev.Phys.Chem.25 201

[2]Pérez-Ríos J,Greene C H 2015J.Chem.Phys.143 041105

[3]Wang B B,Han Y C,Cong S L 2016J.Chem.Phys.145 204304

[4]Wang B B,Han Y C,Gao W,Cong S L 2017Phys.Chem.Chem.Phys.19 22926

[5]Wu C H,Ihle H R 1977J.Chem.Phys.66 4356

[6]Kim S K,Herschbach D R 1987Faraday Discuss.Chem.Soc.84 159

[7]Vezin B,Dugourd P,Rayane D,Labastie P,Broyer M 1993Chem.Phys.Lett.202 209

[8]Siegbahn P,Schaefer H F 1975J.Chem.Phys.62 3488.

[9]Yan G S,Xian H,Xie D Q 1997Sci.China Ser.B:Chem.40 342

[10]Maniero A M,Acioli P H,Silva G M,Gargano R 2010Chem.Phys.Lett.490 123

[11]Song Y Z,Li Y Q,Gao S B,Meng Q T 2014Eur.Phys.J.D68 3

[12]Yuan M L,Li W T,Chen M D 2017Int.J.Quant.Chem.e25380

[13]Kim S K,Jeoung S C,Tan A L C,Herschbach D R 1991J.Chem.Phys.95 3854

[14]Vila H V R,Leal L A,Martins J B L,Skouteris D,eSilva G M,Gargano R 2012J.Chem.Phys.136 34319

[15]Cunha W F,Leal L A,Cunha T F,Silva G M,Martins J B L,Gargano R 2014J.Mol.Model20 2315

[16]Gao S B,Zhang J,Song Y Z,Meng Q T 2015Eur.Phys.J.D69 111

[17]Gao S B,Zhang L,Song Y Z,Meng Q T 2016Chem.Phys.Lett.651 233

[18]Fu B N,Zhang D H 2012J.Chem.Phys.136 194301

[19]Shen P R,Han Y C,Li J L,Chen C J,Cong S L 2015Laser Phys.Lett.12 045302

[20]Pang Y H,Wang B B,Han Y C,Cong S L,Niu Y Y 2016Chin.J.Chem.Phys.29 297

[21]Gao W,Wang B B,Hu X J,Chai S,Han Y C,Greenwood J B 2017Phys.Rev.A96 013426

[22]Yuan J C,Cheng D H,Chen M D 2014RSC Adv.4 36189

[23]Duan Z X,Qiu M H,Yao C X 2014Acta Phys.Sin.63 063402(in Chinese)[段志欣,邱明辉,姚翠霞2014物理学报63 063402]

[24]Zhang J,Wei W,Gao S B,Meng Q T 2015Acta Phys.Sin.64 063101(in Chinese)[张静，魏巍，高守宝，孟庆田2015物理学报64 063101]

[25]Yuan K J,Cheng Y,Liu X H,Harich S,Yang X M,Zhang D H 2006Phys.Rev.Lett.96 103202

[26]Hankel M,Smith S C,Allan R J,Gray S K,Balint-Kurti G G 2006J.Chem.Phys.125 164303

[27]Fu B,Zhang D H 2007J.Phys.Chem.A111 9516

[28]Zhang D H 2006J.Chem.Phys.125 133102

[29]Koslof fR 1988J.Phys.Chem.92 2087

[30]Light J C,Carrington T 2000Adv.Chem.Phys.114 263