基于BP神经网络和聚类分析的任务定价

刘忠青，昝道广

（山东科技大学电气信息系，济南 250031）

0 引言

“拍照赚钱”是基于移动互联网下的一种自助服务模式，用户通过下载并且注册App成为会员后，可以在App上领取拍照任务来赚取App对任务所标定的酬金。相比传统的市场调查方式，通过这种基于移动互联网的自助式劳务众包平台来为企业提供各种商业检查和信息搜集，能够更加节省调查成本，并且能够有效保证调查数据的真实性，且缩短了调查周期。因此APP成为该平台运行的核心，而APP中的任务定价又是其核心要素。如果定价不合理，有的任务就会无人问津，而导致商品检查的失败。

根据附件中所给出的数据，由此考虑以下三个问题：

（1）通过研究附件一中项目的任务定价规律，分析任务未完成的原因。

（2）给出对附件一中的项目设计新的任务定价方案，并与原方案进行比较。

（3）在实际生活中，多个任务可能分布位置十分相近，导致用户会争相选择，可以将多个任务组合在一起打包发布。请思考在该种情况下如何修改前面的定价模型，会对任务的完成情况带来怎样的改变。

（4）请设计出针对于附件三中的新项目的任务定价方案，同时评价定价方案的实施情况。

1 问题假设

（1）假设任务定价不考虑所在位置经济水平与交通因素。

（2）假设每个会员的位置信息、信誉度以及预定限额在完成问题四的新项目时不发生变化。

（3）假设问题三、四中同一类任务的定价相同。

2 多元线性回归描述定价规律

首先进行数据清洗，剔除数据异常项，对附件一、二中的经纬度归一化处理。利用GPSspg软件将附件一中所有经纬度信息导入，查询出已结束任务位置所对应的具体地点。考虑到附件一中任务定价和任务经度、任务纬度、每个任务到所有会员的平均距离有关，故假设任务经度、任务纬度、每个任务到所有会员的平均距离与任务定价之间呈多元线性关系进行分析，建立多元线性回归模型进行定量分析。

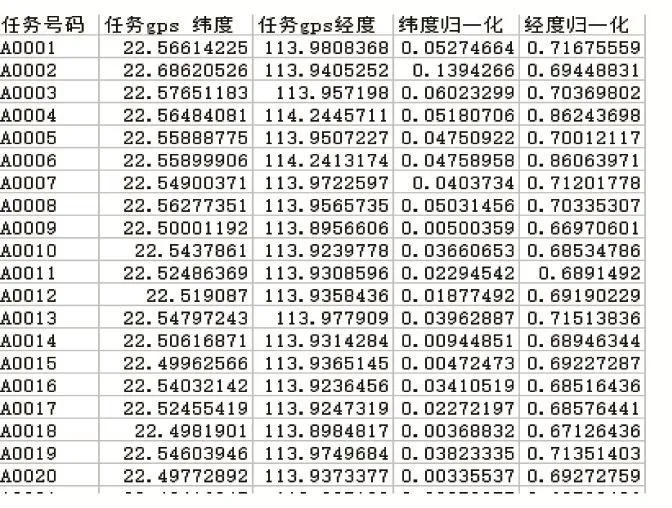
图1 归一化处理结果图

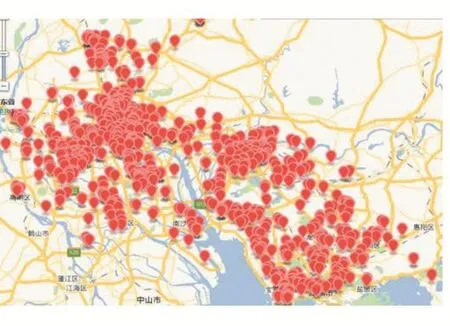
图2 已结束任务地理分布图

首先查阅文献[1]得出由两点的经纬度得出两点的实际地理距离公式:

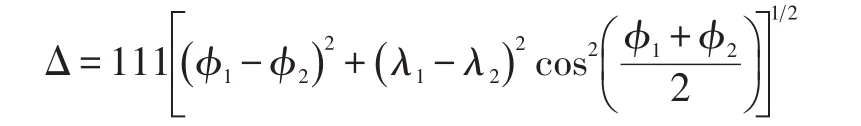
其中Δ为两点之间的距离，λ1，λ2分别为两点的经度，ϕ1，ϕ2分别为两个点的纬度。利用Python得到每个任务到所有会员的平均距离:

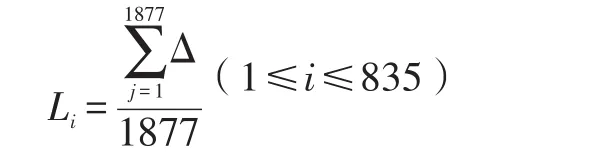
2.1 多元线性回归模型的建立

y=ax1+bx2+cx3+ε

其中y表示每个任务定价，a、b、c指偏回归系数，x1为纬度，x2为经度，x3为每个任务到所有会员的平均距离。

2.2 多元线性回归模型的求解

对附件一中的已结束任务选取前500个样本进行分析。利用MATLAB软件得出各个系数的值，所以多元线性回归模型为：

y=68.6692+1.1129x1+4.4192x2-0.1818x3

R2=0.0239，F 统计量为 6.7809，p值为0.0002，误差方差s2为19.9503。根据回归模型，当p的值大于0.05时，表示所求的系数为合理，显然所得的p<0.05，则根据数据建立的多元线性回归模型成立。

2.3 任务定价规律总结

综上，该多元线性回归模型可以定量的描述任务定价与任务位置以及平均距离之间的关系。因此，将此模型作为附件一中已结束任务定价规律的模型表示。

2.4 未完成原因分析

通过划分任务定价区间，利用MATLAB、Excel得出以下结果图和价格区间完成情况表得出任务未完成度与任务定的高低、任务的位置、会员的位置，以及会员的预定限额与信誉度之间的关系。

图3 已结束任务分布图

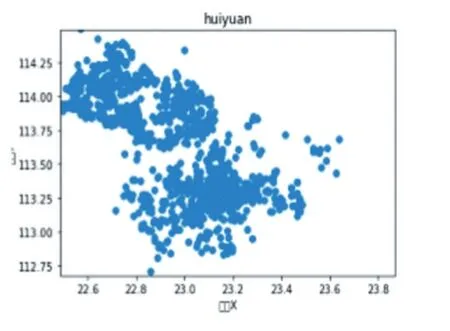
图4 会员分布情况图

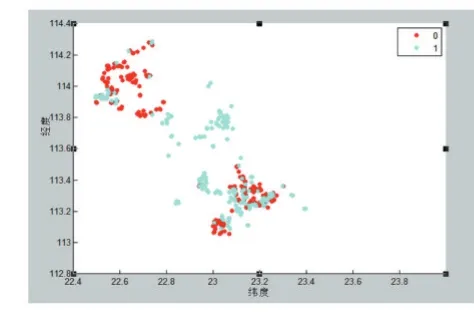
图5 定价区间[68,70.5]

图6 定价区[68,70.5]

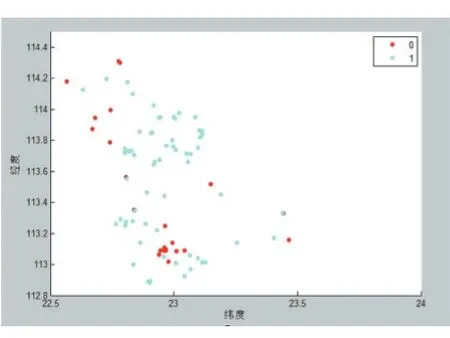
图7 定价区间[71,73.5]

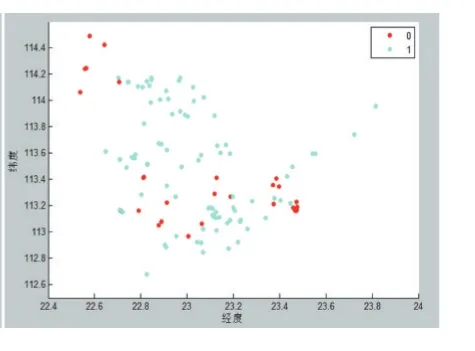
图8 定价区间[74,85]

3 新任务定价方案

结合未完成原因分析，对会员到任务ti的距离li小于等于平均距离Li的每个任务到所有会员的平均距离为半径的范围内的会员的平均信誉度Cˉ与平均预定限额，并归一化处理：

3.1 建立任务定价模型

运用MATLAB软件使用BP神经网络模型，来建立任务定价与任务的经纬度、每个会员到任务的平均距离，以及平均信誉额度与平均预定限额的关系模型，分为输入层、隐藏层与输出层。

图10 BP神经网络模型构造示意图

（1）输入层

通过以上对附件一中的数据处理和优化最终得到513条任务完成度为1的数据，将其中的400条数据作为训练集输入，123条数据作为测试集输入用于验证关系模型的正确性。

（2）隐藏层

通过建立两层隐藏层进行训练，第一层为15个神经元，第一层为20个神经元。使用tansig(s)函数和purelin(s)函数对每个隐藏层的接收到的数据进行处理。

（3）输出层

使用输出层输出任务定价的预测数据，即任务的定价值。

通过MATLAB运行训练集的数据得到任务定价模型：

Y1=f2(f1(x1W1+b1)×W2+b2)

其中：

然后对神经网络模型利用123条测试数据进行验证，则得到以下结果：

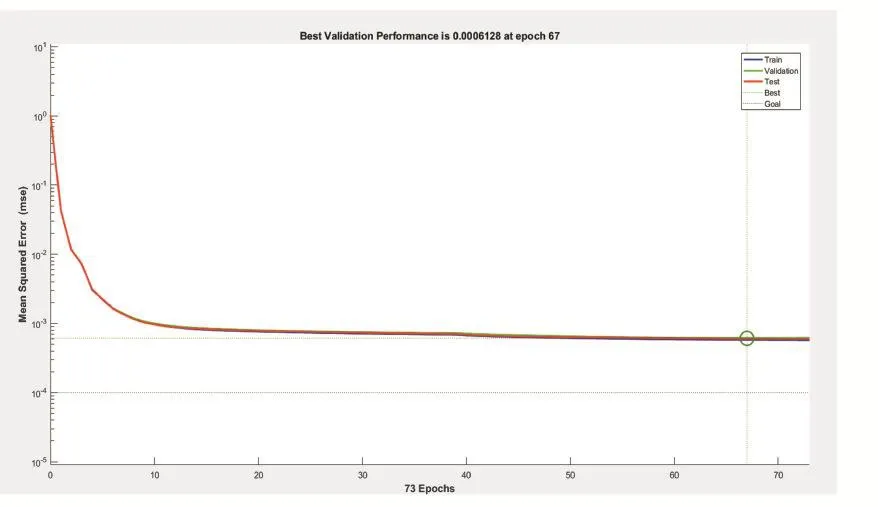
图11 数据拟合曲线图

最后以300条任务完成度为0的数据作为输入，得到一个新的定价方案为：

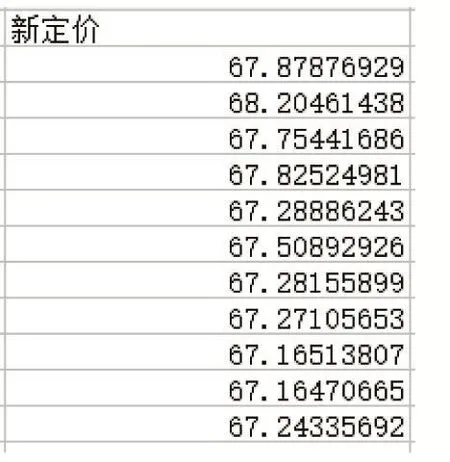
图12 新价格方案任务价格示意图

3.2 完成度逻辑回归模型的建立

对附件一所有已结束任务进行逻辑回归模型的建立，以任务经度、任务纬度、每个任务到所有会员的平均距离、每个任务的会员平均信誉值、以为自变量及任务定价为因变量，建立完成度回归模型。将数据导入SPSS，得出完成度F模型：

F=1.21x1+3.219x2-0.098x3+0.013x4+0.095x5-9.24

式中：x1为任务经度，x2为任务纬度，x3为每个任务到所有会员的平均距离，x4为可能做该任务的所有会员的平均信誉值，x5为可能做该任务的任何会员平均预定限额。

3.3 利用F模型与完成度比较

利用F 模型仅对附件一中任务完成度为0的任务进行重新定价，得出重新定价之后的任务完成情况表

表1 重新定价完成情况比较

由表1可知，该方案的定价比原方案更合理，在一定程度在提高了任务完成率。

4 打包重新制定定价方案

由于已结束任务分布十分密集，可以通过在同一时间点发布任务进行打包，即通过提高同一时间点打包发布的任务数目来降低竞争程度大小。通过聚类分析将任务划分为k类，使k类任务中的每一类的发布时间相同。聚类分析的具体步骤如下：

（1）通过附件一得出已结束任务经度范围属于[22.49,23.87]，已结束任务纬度范围[112.68,114.49],分别在两个经度、纬度范围内通过Python程序随机k次，得出k个初始中心经纬度位置(ci,bi)（i=0,1,2，…，k）。

（2）首先对每个任务在k个中心点中找出距离最近的中心点ki，则A0j任务属于以ki为中心的一类。通过求出中心点ki与每个任务的中心点作为新的ki。

（3）然后再进行下一个任务的计算，重新进行第二步。将最后一个任务归类完毕。得到每个任务类的中心点经纬度和每个任务的分类结果。

所有任务分为23类，通过将聚类得到23个中心点的经纬度(ci,bi)，同问题二利用Python编程求出每类任务到所有会员的平均距离、每个任务到所有会员的平均距离、每个任务的平均信誉值，如下图：

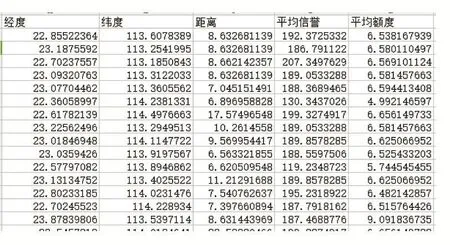
图13 任务中心所求示意图

再利用定价模型Y得出k类任务定价，假设每一类中的任务定价相同，即属于第i类的所有任务定价均为zi，利用问题二中已求数据平均距离、平均信誉值、平均预定限额分别代入到问题二任务完成度模型F中，得出每类任务中的完成数目，得出附件一中已结束任务打包前后任务完成情况表以及每个任务中心点的定价方案：

图14 任务中心定价方案情况示意图

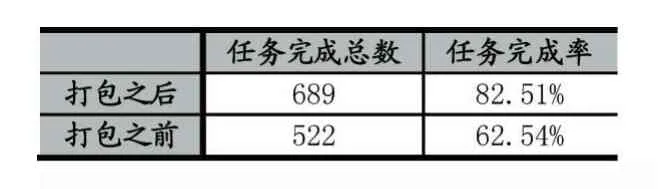
表2 打包前后效果分析图

由表2可知，打包之后任务完成度提高了20.03%，所以通过在同一时间点内打包发布任务有利于提高完成度。

5 定价模型的应用

用Excel画出新任务的分布，可以看出任务分布极其集中，这样会使用户争相选择，会严重增大会员的竞争激烈程度。故采用在同一时间点发布的原则进行打包，通过聚类分析分为K类，利用Python编程求出每一类任务的中心点的经纬度位置(ci,bi)，并数据处理求解出可能做该任务的所有会员的平均信誉值、可能做该任务的所有会员的平均预定限额，进而运用定价模型Y得出每类任务定价，将K个定价分别代入F模型，得出K类中每类任务的完成个数，将K类所有的任务中心点，最后得出结果：

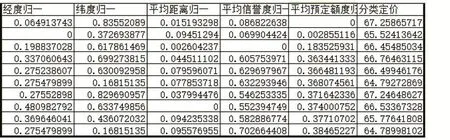
图15 新任务中心定价方案情况示意图

表3 新任务效果分析图

6 结语

本文通过研究已有的任务定价，分析未完成任务原因，在原基础上改进任务定价方案，对任务进行打包分布，重新得出定价方案，应用于不同的任务定价中。经过验证，改进后的任务定价方案提高了任务完成度。

[1]韩忠民.知经纬度计算两点精确距离：科技传播：2011，11.

[2]姜启源，谢金星.数学模型，北京：高等教育出版社，2010，9,

[3]韩婷，王金宝.数学建模入门与提高，北京：国防工业出版社，2013，8.

[4]叶其孝姜启源.数学建模，北京：机械工业出版社，2009，8.

[5]方道元，韦明俊.数学建模，杭州：浙江大学出版社，2011，2.