基于在线测评系统的编程题目难度研究

陈荟慧，熊杨帆，蒋滔滔，李佳

（重庆大学计算机学院，重庆 400044）

1 研究背景及意义

自进入21世纪以来，几乎全民都在制造数据，大数据这个话题进入了各界学者的讨论范围。数据分析是组织有目的地收集数据、分析数据，使之成为信息的过程。数据分析的目的是把隐没在一大批看来杂乱无章的数据中的信息集中、萃取和提炼出来，以找出所研究对象的内在规律。

程序在线测评系统，起源于ACM/ICPC国际大学生程序设计竞赛，是为培训该程序竞赛参赛人员开发的，但是在培训过程中，研究人员发现，OJ系统在大学生程序设计类课程的教学中也能发挥很大的作用，于是OJ也渐渐走入相关课程的教学中。很多高校都开发出了自己的OJ系统，其中较为著名的有浙江大学Online Judge（ZOJ）、北京大学 Online Judge（POJ）、同济大学 Online Judge（TOJ）、西班牙 Valladolid大学 Online Judge（UVA）等，值得一提的是，在本研究的过程中，重庆大学也收获了自己的OJ系统，重庆大学Online Judge（CQUOJ）。

对OJ系统中的题目进行难度研究，是因为在线学习的学习者的编程能力良莠不齐，如何在练习的过程中对水平不同的学习者推荐有针对性的题目，是近年来OJ系统要解决的难题。而现在的多数OJ系统里的题目难度是靠做题人的主观经验手动完成的，费时费力。OJ系统中保存着大量的测评数据，这些测评数据直接或间接反映了学习者的学习行为，我们就利用OJ系统中的原始数据，从中随机抽取部分数据作为研究样本，综合考虑各项因素，最终选择对题目难度研究最有效的特征集，利用这些特征创建分类模型，为在线测评系统上的题目作自动分类预测。

2 研究设计

2.1 研究材料

本研究的实验数据来自著名的在线评测系统Codeforces，Codeforces是一家为计算机编程爱好者提供在线评测系统的俄罗斯网站。选择该系统，是因为Codeforces是众多OJ系统中为数不多的为编程试题提供难度分类的系统。系统标记的经验难度参数作为本研究中决策树分类成果的检验标准，测试模型性能。

实验数据选择的是Codeforces上2016年12月-2017年12月时间段内100多场比赛里的题目提交记

2.2 研究工具

本研究使用的工具中最重要的是scikit-learn包（简称sklearn），在机器学习和数据挖掘的应用中，sklearn是一个功能强大的Python包。实验中主要使用的部分就是sklearn.tree，模块自带的决策树方法，它分为两个决策树模型，分别是DecisionTreeClassifier()分类决策树模型和DecisionTreeRegressor()回归决策树模型。由于本研究是为了给不同题目分配不同的难度类型，实验中使用的是分类决策树模型。scikit-learn中决策树的可视化使用的是graphviz。

2.3 研究步骤

录，每场比赛有5-7题，按经验分别被标记为ABCDEFG类，共600道题，其中2/3的题目用作训练集，1/3的题目用作测试集。每场比赛的提交记录最多可到达25000条，共200多万条提交记录数据。

以Codeforces上采集的原始评测数据为分析对象，而原始数据往往存在错误和噪音点，所以首先要对实验数据做清洗处理。其次进行数据归一化，更方便观察特征之间的可比性，然后根据选择出的特征集，结合决策树算法创建分类模型，以达到在线题目难度划分的目的，最后通过调整模型参数和剪枝操作，不断优化分类模型，得到最优方案，具体步骤如下：

（1）数据的采集

为了使采集的样本更客观地反映题目难度，样本选择的是Codeforces线上比赛的提交记录样本，因为一般在比赛上进行练习时，不仅有合理的时间限制，而且学习者能够更专心，较少受到主观因素的打扰，这个时候的测评数据更能反映题目的客观难度。采集数据的过程是利用python编写的爬虫脚本来完成的，首先确定爬取的比赛编号，然后确定该场比赛的开始时间与时长，爬取比赛时长内所有提交记录。获取的每条原始记录有很多特征值，如用户名、用户提交时刻、提交的题目难度类型、测评结果、程序运行时长、运行所占内存等。

（2）数据的清洗

从Codeforces上爬取的全部都是原始数据，而且后期的用于创建模型的数据是经过汇总的数据，汇总时也可能遗漏数据，所以在进行数据分析之前，首先作数据预处理。预处理操作是对原始数据进行数据空值和错误值的检测和清洗，除去孤立数据，将噪声数据产生的影响降到最低。

（3）数据的归一化

数据归一化化就是要把需要处理的数据经过处理后（通过某种算法），限制在需要的一定范围内。归一化是为了后面数据处理的方便，保证程序运行时收敛加快。本研究中的用于机器学习的样本，是提交记录汇总后的没类难度类型的题目提交情况，每个样本中包含的属性有题目编号、题目难度类型、题目总的提交次数、题目总的通过次数（简称总AC量）、题目首次提交即通过的次数（简称1A量）、通过时的总用时（简称AC总用时）。属性的取值多是整型和浮点型，取值范围较大，不利于模型的训练，所以在不影响总体结果的前提下，对数据进行归一化，产生了AC率和1A率，以及AC平均用时。

（4）模型的创建

在创建模型时，尝试不同的特征子集，创建不同的决策树模型，并通过后期的剪枝过程，不断优化模型的性能，选出最优分类模型。

3 算法及关键技术

根据上一章节的内容我们知道，本研究中的分类模型如图1所示，接下来介绍在研究过程中的算法及关键技术。

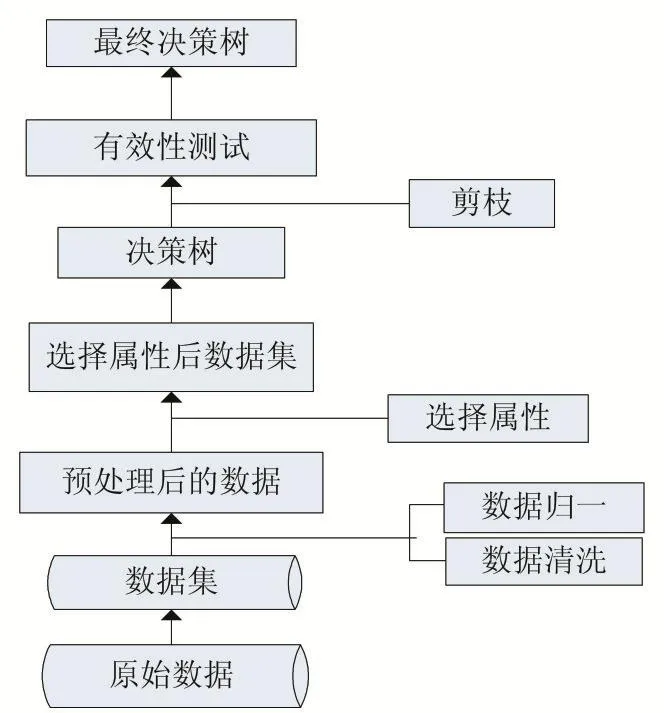
图1 分类模型

3.1 决策树分类算法

本文使用决策树中的CART(Classification And Regression Tree)算法对数据进行监督分类，CART算法采用一种二分递归分割的技术，将当前的样本集分为两个子样本集，使得生成的每个非叶子节点都有两个分支。CART算法由以下两步组成：

决策树生成：基于训练数据集生成决策树，生成的决策树要尽量大。

决策树剪枝：用验证数据集对已生成的树进行剪枝并选择最优子树。

（1）决策树生成

上面说到CART算法分为两个过程，其中一个过程进行递归建立二叉树。

设 X1，X2，...，Xn代表单个样本的 n个属性，Y 代表所属类别。CART算法通过递归的方式将n维的空间划分为不重叠的矩形，划分时的具体操作是：选一个自变量Xi，再选取Xi的一个值vi，vi把n维空间划分为两部分，对于连续变量，一部分的所有点都满足Xi≤vi，另一部分的所有点都满足Xi>vi,对非连续变量，属性值的取值只有两个，即等于该值或不等于该值。

在划分的时候还有一个问题，选择特征属性和分裂点的标准是什么。对于CART算法来说，它采用Gini指数来度量分裂时的不纯度，之所以采用Gini指数，是因为较于熵而言其计算速度更快一些。

具体的，在分类问题中，假设有K个类别，在决策树的节点t处，第k个类别的概率为P(Ck|t)，Gini指数计算公式如下：

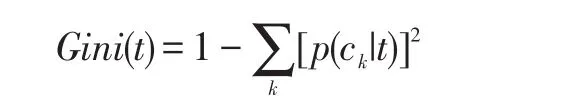
Gini指数即为1与类别Ck的概率平方之和的差值，反映了样本集合的不确定性程度。Gini指数越大，样本集合的不确定性程度越高。分类学习过程的本质是样本不确定性程度的减少（即熵减过程），故应选择最小Gini指数的特征分裂。父节点对应的样本集合为D，CART选择特征A分裂为两个子节点，对应集合为DL与DR；分裂后的Gini指数定义如下：

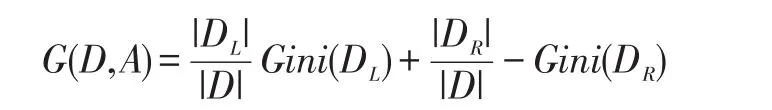
其中，|⋅|表示样本集合的记录数量。

综上所述，CART分类算法建立树的具体流程如下：

①对于当前节点的数据集为D，如果样本个数小于阈值或者没有特征，则返回决策子树，当前节点停止递归。

②计算样本集D的基尼系数，如果基尼系数小于阈值，则返回决策树子树，当前节点停止递归。

③计算当前节点现有的各个特征的各个特征值对数据集D的基尼系数。

④在计算出来的各个特征的各个特征值对数据集D的基尼系数中，选择基尼系数最小的特征A和对应的特征值a。根据这个最优特征和最优特征值，把数据集划分成两部分D1和D2，同时建立当前节点的左右节点，左节点的数据集D为D1，右节点的数据集D为D2。

⑤对左右的子节点递归的调用①-④步，生成决策树。

（2）决策树剪枝

由于决策时算法很容易对训练集过拟合，而导致泛化能力差，为了解决这个问题，我们需要对CART树进行剪枝，来增加决策树的返回能力。CART采用的办法是后剪枝法，即先生成决策树，然后产生所有可能的剪枝后的CART树，然后使用交叉验证来检验各种剪枝的效果，选择泛化能力最好的剪枝策略。

3.2 特征提取

爬取到的原始数据集经过统计，汇总出训练数据集。在建立分类模型之前，先要根据训练数据集提取特征集，在提取特征之前，我们首先对训练数据集中的各个特征之间的关系进行了分析，选择出对编程题目难度研究最为有效的特征。

（1）数据汇总

上文提到，原始数据是一条条的提交记录，显然，直接使用原始数据集训练分类模型是不可行的，必须对提交记录进行汇总，得到关于题目的统计数据作为训练集，创建分类模型。原始数据包括的属性很多，实验中只统计可能影响题目难度的数据。汇总时，以题目编号为关键字，统计一场比赛中该题的总提交次数、结果为“Accepted”的总次数、首次提交就“Accepted”的次数、结果为“Accepted”的总用时。其中“Accepted”用时是通过记录提交时间减去比赛开始时间得到的。

（2）特征粗提取过程

训练数据集中题目难度是离散化的几种类型，没有达到难度量化的程度，在研究初始时，我们就根据之前的经验认为AC量在一定程度上可以表示量化的题目难度。所以我们首先尝试着去分析不同难度类型的题目AC量分布情况。图2是每种类型试题的平均AC量分布情况。

图2 平均AC量对比

图2的平均AC量对比情况显示了7种不同类型的题目AC量分布状态。由这些图可知，不同题目AC量集中分布的量和范围因题目难度类型的不同而有明显的不同，因此我们确定了样本中AC量为首要研究的自变量特征。

仅仅考虑AC量时，会遇到一种情况：当一个学习者在做练习时，经过多次提交代码，最终运行出正确结果，即通过了该题，为了优化解题过程，学习者可能会多次修改代码并提交通过，这样就提高了AC量，使得这个特征不能那么客观地反映题目的难度类型。于是在分析样本集时我们注意到了另一个很重要特征，1A量，即学习者首次提交就通过的次数。1A量不仅能有效体现题目难度类型，而且不存在重复提交的问题。

在处理数据时我们还得到如图3的结论，学习者通过题目的平均用时越长，说明题目难度越大。所以把采集到的原始数据中AC总用时，即题目AC的提交时间与首次提交时间的差值之和，也作为研究对象的自变量特征。从这个变量可以看出某题从开始提交到通过的用时。

图3 AC平均用时

通过以上分析，我们最终选择AC量、1A量、AC总用时为模型研究的初始自变量特征。此时，对于题目Num_P_i使用（X1，X2，X3）三维特征来表示，其中 Num_P表示比赛的场次，i表示题目的经验难度类型，取值范围是{A,B,C,D,E,F,G}，X1是 AC 量，X2是 1A 量，X3是 AC总用时。

（3）特征再处理

①AC率：在使用AC量作自变量特征时还有一处不足，那就是在不同场比赛中，参赛的用户数量不尽相同，总提交量、AC量可能存在差异过大的个别现象，所以为题目添加了另一个特征AC率，X4=AC量/总提交量。

②1A率：与AC量这个特征类似，1A量也是一个绝对量，也存在与AC量一样的不足，所以用1A率替换了1A量这个特征，X2=X2/AC量。

③AC平均用时：上文中使用了AC总用时作为研究特征，但是在创建模型的过程中发现AC总用时的取值范围太大，并不利于模型的创建，所以将AC总用时替换为AC平均用时，X3=X3/AC量。

综合以上，题目 Num_P_i使用（X1，X2，X3,X4）四维特征来表示。

4 实验分析

4.1 采集数据

（1）原始数据集

我们知道，用于研究的原始数据是从OJ系统上爬取的多场比赛中学习者的提交记录，在一场比赛中收集到的每条原始数据最主要内容如图4所示。

图4 部分原始数据集

从上面的截图可以看出，每一条原始记录最主要的特征属性有提交ID、提交时刻、提交用户、题目名称、使用语言、运行结果、运行时间、运行内存、题目难度类型。每一个用户对同一道题可提交一到多次。

（2）训练数据集

通过将原始数据集里的提交记录按照题目编号统计汇总，最终得到以题目编号为关键字的训练数据集，其主要内容如下截图所示。

4.2 特征值数量分析

以难度类型ABCDEFG的题目为例，选择四元组特征集，对创建的分类模型分析。使用X1，X2，X3,X4四个特征变量执行分类算法，对分类结果的测试如下表1所示。

表1 预测结果

4.3 实验结果分析

分析表1我们发现，ABC难度类型的题预测正确率超过了65%，D类型预测正确率52.78%，但是EFG类题目的预测正确率低于50%。之所以会产生如此低的正确率，是有原因的。在Codeforces系统上的比赛中，EFG类题目已经属于难度很大的题了，做题的人数很少，导致提交记录很低，对这类题的训练度明显不够。这种情况下创建的分类树对EFG类题目进行预测时，并不能达到预期的结果，所以对树的优化必不可少。

4.4 模型优化

从对实验结果的分析可知，EFG类题目属于难度较大的题目，提交量不足、训练度不够，达不到预期结果，所以在优化分类树时，将这三类题目当做同一类题目处理，记作P难度类型。提交量这一因素处理影响了对EFG类题目的分类外，还影响了每种题目的AC量，而AC量在创建二叉树时起到了很重要的作用，所以AC量的起伏过大对分类结果的影响也很大。于是我们将AC量作用在log()函数上，这样就缓和AC量的过大波动，优化了分类树。

通过以上优化方法，分类树的性能得到了很大的提高。

[1]郭嵩山,王磊,张子臻.ACM/ICPC与创新型IT人才的培养[J].实验室研究与探索，2007:188-192,196.

[2]李文新，郭炜.北京大学程序在线测评系统及其应用[J].吉林大学学报，2005.8（23）：171-177.

[3]郭嵩山,王磊,张子臻.ACM/ICPC与创新型IT人才的培养[J].实验室研究与探索，2007:188-192,196.

[4]范玉玲,徐涛,王钦.基于在线测评数据的题目等级分类模型研究[J].计算机与现代化，2017：3（259）：37-38.

[5]姚孟臣.数量化方法在试题难度中的应用[J].数理统计与管理，1993.2（2）：21-27.

[6]John D.Kelleher,Brian Mac Namee,Aoife D'Arcy.Fundamentals of Machine Learning for Predictive Data[M].Publisher:The MIT Press,2015-7-24.