基于属性模型构建的社交网络的链路预测

周明强，王莹

（重庆大学计算机学院，重庆 400044）

0 引言

社交网络是Web2.0的一种典型应用即社会性网络服务（Social Networking Service，SNS），也是复杂网络中的一个特例。链路预测是指如何通过已知的网络结构等信息预测网络中尚未产生连边的两个节点之间产生连接的可能性，它既包含了对未知链接的预测，也包含了对未来链接的预测。社交网络链路预测，就是分析社交网络的链路预测，它对信息检索和电子商务中的推荐系统有着关键的作用，可以从最终的链接关系着手帮助使用者找到新的推荐用户和潜在用户，在网上购物提供合理和贴切的推荐。

如何在社交网络中准确进行链路预测，就要考虑到社交网络本身的特点，社交网络的链接在多大程度上可以使用网络本身固有的特性来建模，问题是网络和节点如何相互关联。真实的社交网络通常具有丰富的结构特征，如同质性、异质性和核心-外围性等。如果能够找到网络结构和辅助信息之间的联系，则可以在一定程度上恢复缺失的链路信息。从技术角度来看,如何构建一种以原则性方式将节点（用户配置文件信息）、边（交互）的功能与网络结构组合在一起的方法是核心问题。

1 问题的相关研究

在传统的链路预测问题中，对于无向网络G(V,E)，其中V={v1,v2,…vN}是节点集合，E={e1,e2,…eN}是边的集合，N与M分别是节点数和边数。一个图的邻接矩阵记为A，无向网络中节点x和节点y对应的连接情况记为axy，当且仅当节点vx与vy之间有连边时axy=1，否则 axy=0，如下所示：

计算节点对之间的相似度是链路预测的直观解决方案。它是基于简单的想法：越是相似的一对，他们之间联系的可能性越大，反之亦然。通过相似性测量，其中每个非连接节点对（x，y）的评分分值高表示X和Y之间的相似性，同时预示着X和Y在未来会联系在一起的概率很高，而低分也表示x和y不连接的概率高。

社交网络中常常出现孤节点的情况，即出现用户节点仅拥有初始的配置信息，提出了基于社交网络拓扑结构和辅助信息进行社交网络链路预测的算法。通过对社交网络的用户配置信息进行用户属性建模，提出了基于MAG模型社交网络用户辅助信息来衡量用户间产生链接的关系强度指标，避免了采用单一指标无法准确度量用户的孤立点问题，使基于社交网络的用户链路预测能够达到更好的算法效果。

基于社交网络和传统网络的区别，社交网络预测问题定义如下：

定义1社交网络图：给出一个社交网络图G（V1,V2,E,NF1，NF2），其中节点 v∈G·N，e∈V1·V1。NF1为V1的节点属性，NF2为V2的节点属性。

2 基于属性模型构建的社交网络的链路预测算法实现

针对属性模型构建的社交网络，这里使用MAG模型对这个网络进行建模，从而推断网络的生成。这里为了对选取的节点属性进行选择，将网络中的节点建模为一个潜在特征向量，并且对每对节点之间的连接可能性进行建模。这里我们使用一种乘法属性模型，这种模型可以根据节点的属性进行建模。

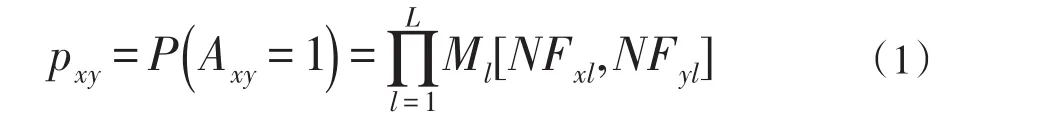
在公式（1）中，Axy为邻接矩阵，Ml为亲和力矩阵，NFxl、NFyl为节点x，y的属性向量。所以需要根据属性估计亲和力矩阵Ml，如图为根据xy的各自的属性向量来模拟xy间连接的可能性，通过亲和力矩阵量化属性对取值对连接的强度的影响以此来考量xy连接的可能性。

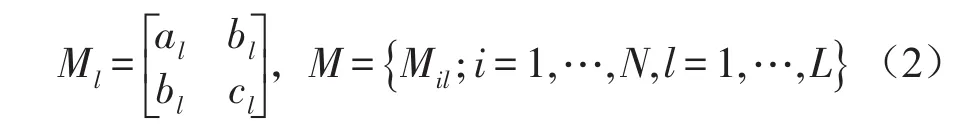
将用户属性按二元的方式用向量进行表示，将数据用邻接矩阵的方式表示。由定义1可知我们将节点集划分为两个部分孤立节点部分，连接节点部分。如图1中，当x的属性向量为（0,1,1，…,1）,y的属性为（1,1,1，…,0）,根据属性对值（0,1），（1,1），（11），（1,0）在指定的属性的亲和力矩阵中找到强度值，用强度值得乘积来量化xy连接的可能性。

同时使用最大似然估计的方法对亲和力矩阵进行估计M，简单地考虑每个属性只有2个取值，若所有属性都是独立存在的，则满足伯努利分布,使用u来表示NF的分布情况，利用最常用的优化方法变分期望最大化（EM）方法来解决网络表示学习问题。

问题表示如下：

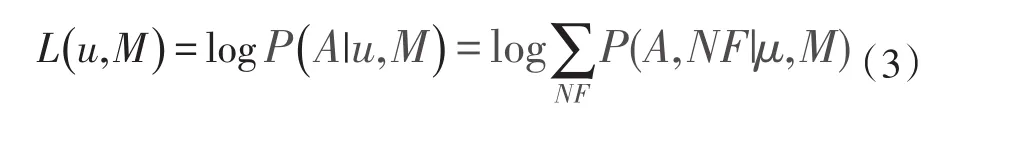
图1

基于属性模型构建的社交网络的链路预测算法（简写为NFLP算法）下面给出具体的算法描述：

输入：输入节点属性列表，G的邻接矩阵A

输出：输出预测的连接列表

步骤1从节点属性列表按照定义生成属性向量形成矩阵NF1，NF2

步骤2根据矩阵NF1，A估计亲和力矩阵M

步骤3根据亲和力矩阵M和矩阵NF2估计预测的连接列表

步骤4按分数值进行排序，取前K名的连接节点输出到连接列表

3 实验结果和分析

本实验采用斯坦福大型网络数据集合（http://snap.stanford.edu/data）上获得的社交网络数据集。为了获得真实的节点属性，我们使用与数据集中相同的协议。节点属性来自用户配置文件，如性别、职位、机构等。使用数据集的基本拓扑情况如表1所示，本实验的硬件环境如表2所示：

表1 数据集的基本拓扑特征

表2 实验硬件环境

经过实验，将属性映射到9个潜在属性得到的分布情况如下：

表3 潜在属性的分布情况

从实验产生的亲和性矩阵为如下：

表4

由于社交网络的稀疏性，链路预测问题在本质上是非常困难的二元预测问题。其中，实际上只有很小一部分的链接存在，如现有连接链路占所有可能连接链路的百分比非常小。与许多现有的链路预测实验类似，这里使用最常用的指标AUC（受试者工作特征下的面积）来测量算法的精确值，AUC值可以被解释为随机选择的不可观测链路比随机选择的不存在链路具更高的分数的概率，预测算法越准确。计算方法如下所示：

为了和该算法形成对比，这里使用传统的链路预测方法进行对比实验：

公共邻居（Common Neighbors）CN指标：若节点x的邻居集合为Γ（x）,节点 x的邻居集合为Γ（y）,若两者之间存在交集的节点越多，则节点x和节点y更相似。CN定义如下：

余弦接近性（Salton Cosine Similarity）Salton指标，定义如下：

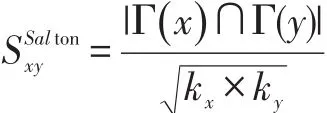
Jaccard指标：一种计算个体间相似性的相似性指标。Jaccard指标的基本思想是，当节点对的共同邻居数越多，则说明它们有更大的相似性，则Sxy就越高。同时，当节点对的两个节点的度越低时，则说明它们的共同邻居所占的比重就越大，在社交网络当中，就说明了两个用户具有更大的共同交际范围，此时他们也就更有可能成为新的好友，即形成新的连接。

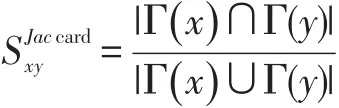
大度节点有利（Hub Promoted，HPI）指标，常常用于生物领域的拓扑相似程度。对比实验结果如表，在给定的数据集中，提出的链路预测算法优于其他方法。

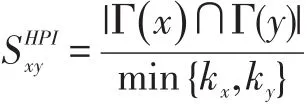
表5 算法AUC对比图

图2

4 结语

如何利用属性信息准确地推断网络中的孤立用户链路是链路预测中的一个难题。许多传统的链路预测方法已经被提出，并且对链路预测问题的解决方案确实起了很大的作用。由于无法找到孤立用户的拓扑结构信息，大多数传统方法不能很好地解决孤立节点的预测问题，但孤立节点往往是最有可能产生连接的节点。基于MAG模型对属性值对节点对生成连接的可能性进行联合，该算法可用于解决实际工作中的相关问题，具有一定的实际意义。并采用Facebook数据集进行试验，证明算法可以达到比较好的结果。

[1]吕琳媛.复杂网络链路预测[J].电子科技大学学报,2010,39（5）:651-661.

[2]Bhattacharyya P,Garg A,Wu S F..Analysis of User Keyword Similarity in Online Social Networks[J].Social Network Analysis and Mining,2011,1（3）:143-158..

[3]黄嘉烜,金小刚.Continuous Multiplicative Attribute Graph Model[J].Journal of Shanghai Jiaotong University（Science）,2017,（01）:87-91.

[4]Akcora C G,Carminati B,Ferrari E.User Similarities on Social Networks[J].Social Network Analysis and Mining,2013,3（3）:475-495.

[4]J.McAuley and J.Leskovec.Learning to Discover Social Circles in Ego Networks.NIPS,2012.

[5]J.McAuley and J.Leskovec.Learning to Discover Social Circles in Ego Networks.NIPS,2012.

[6]Anderson A,Huttenlocher D,Kleinberg J,et al.Effects of User Similarity in Social Media[C].Proceedings of the fifth ACM International Conference on Web Search and Data Mining,2012:703-712.