基于自然邻居改进的DBSCAN算法
李捷,陈雁彬
(重庆大学计算机学院,重庆 400044)
0 引言
在数据挖掘中,聚类算法占据重要地位,它是按照一定的规律和方法对事物进行区分和归类[1],而聚类算法细分为基于层次的聚类方法、基于划分的聚类算法、基于密度的聚类算法与基于网格的聚类算法,基于密度的聚类算法是聚类中的一个重要的研究分支,相比于其他算法,基于密度的聚类算法可以在有噪声的数据中发现各种形状与各种大小的类别,DBSCAN[4]是该方法中最典型的代表算法之一,其核心思想是首先发现具有高密度的点,然后将相邻近的高密度点逐步的连接在一起,进而形成各种簇;由于DBSCAN算法使用的是全局的密度阈值MinPts,只能发现密度不少于MinPts的点组成的簇,无法发现不同密度的簇,为了解决这些问题,OPTICS[5](Ordering Points to Identify the Clustering Structure)算法将邻域点按照密度大小进行排序,最后使用可视化的方法来发现不同密度的簇,然而该方法需要在可视化的图上查找“山谷”,进而发现簇,因此算法性能直接受到这些可视化方法的约束;SNN(shared Nearest Neighbor)算法采用一种基于KNN方式计算相似度的方法来改进DBSCAN,其核心思想是在空间中找出离其最近的k个点,两个点的相似程度使用这两个点的k邻域范围中共享的近邻数量来度量,然而SNN算法需要设定近邻个数k,且该算法的性能对k的取值很敏感。
基于以上分析,考虑到数据集中可能存在不同形状、不同密度的簇,本文提出一种使用自然邻居算法进行改进的DBSCAN算法,以后称作NN-DBSCAN算法,首先对整体数据集使用自然邻居算法得出该数据集中点的邻域分布情况,然后使用核心点选取算法筛选整体数据集,得出核心点,然后对核心点集再次使用自然邻居算法,得出核心点之间的关系,接着每个核心点使用最大逆邻居距离作为该点的邻域半径值,若两个核心点的距离都在其对应的邻域半径之内,则两个核心点属于同一个类别,对筛选掉的点,算法采用第一次使用自然邻居算法得到的核心点的最大逆邻居距离来归类。
1 自然邻居搜索算法
1.1 自然邻居
自然邻居是一种新的邻居概念,它记录了在k邻域范围内,存在多少个点将已知点当作邻居的信息,在此同时也记录了该点与k个邻居点集合中的互为邻居点的信息[15];由此可知,在数据集中分布较为稀疏的部分,数据点拥有较少的自然邻居点,反之,在分布较为集中的部分,数据点将拥有较多的自然邻居[3]。
1.2 自然邻居搜索算法
自然邻居的核心思想是在一个连续的搜索范围内,递增邻域范围值k,每次递增都会查找每个点的自然邻居,直到所有点都有自然邻居或者没有自然邻居的点的数量在一定搜索次数内不再发生改变[3]。
算法1:自然邻居搜索算法
输入:数据集D
输出:自然邻居特征值supk,数据点自然邻居数量nb,数据点自然邻居记录NN
初始化supk=1,nbi=0,NN0(i)=∅,RNN0(i)=∅
While true
Foreachpiin D
使用kdtree搜索 pi点的第supk近邻 pj
更新pj点自然邻居数量nbj=nbj+1
NNsupk(i)=NNsupk-1(i)∪{j}
RNNsupk(j)=RNNsupk-1(j)∪{i}
Endfor
计算没有逆邻居的点的数量Numb
IfNumb未反生改变
Break;
Endif
supk=supk+1
Endwhile
supk=supk-1
输出supk,nb,NNsupk
自然邻居搜索算法采用kd树进行索引,该算法时间复杂度为O(nlogn+nsupk),且通过大量实验可知,自然邻居特征值supk远小于数据集规模n(一般在1到30之内),所以该算法的时间复杂度为O(nlogn)。
2 NN-DBSCAN算法描述
NN-DBSCAN算法分为三步,首先使用自然邻居算法得出数据集的中每个数据点的邻域信息,然后使用这些邻域信息选取出核心点集合;然后再次使用自然邻居算法对核心点进行处理,得出核心点之间的邻域信息,使用这些信息计算出每个核心点的邻域半径值,并将互相处于自身邻域半径值范围内的两个核心点划归为同一类别;最后,对每个非核心点,使用第一次自然邻居算法得出的邻域半径,找出和其互在自身邻域半径范围内的核心点,取这些核心点中最近的点的类别作为该点的类别,对没有归类的非核心点,算法判定为噪声点。
2.1 基于自然邻居算法的核心点选取算法
在聚类过程中,本文采取的邻域半径值ε为各个数据点到其所有自然邻居的距离的最大值,这个值很大程度上会受到噪声点的干扰,因此需要一步粗处理来去除这些干扰点;干扰点去除算法的核心是判断数据点i的自然邻居数量是否不小于其supk邻域内数据点的平均自然邻居数量,若是,则将数据点i放入核心点集合中,否则去除。
算法2:核心点选取算法
输入:数据集D
输出:核心点集合Core
初始化Core=∅
对原始数据集D使用自然邻居搜索算法得到supk和nb
Foreachpiin D
sum=0
Forj=1tosupk
使用kdtree搜索 pi点的第 j近邻 pq
sum=sum+nb(q)
Endfor
Ifnb(i)≥sum/supk
Core=Core∪{i}
Endif
Endfor
输出Core
核心点选取算法能够将簇的大部分边缘点和几乎所有的噪声点都筛除掉,既保留了原始数据集中簇的结构,也过滤掉了噪声点的干扰;其时间复杂度为O(nlogn+nsupklogn),由于supk远小于n,所以最终复杂度为O(nlogn)。
2.2 核心点聚类算法
核心点聚类算法的核心是使用自然邻居算法对筛选之后的数据点集合进行处理,得出筛选点之间的邻域关系,然后使用每个保留点的最大逆邻居距离判断两个保留点是否属于同一个簇,若两个保留点互在其对应最大逆邻居距离范围之内,则两个点属于同一类别,算法描述如下:
算法3:核心点聚类算法
输入:核心点集合Core
输出:核心点聚类结果Clusters
初始化N=num(Core),Clusters=1 to N,MaxDisti=0
对核心点集合Core使用自然邻居算法,得到nb,NNsupk
Foreachpiin Core
ForeachpjinNNsupk(i)
dist=EuclideanDist(pi,pj)
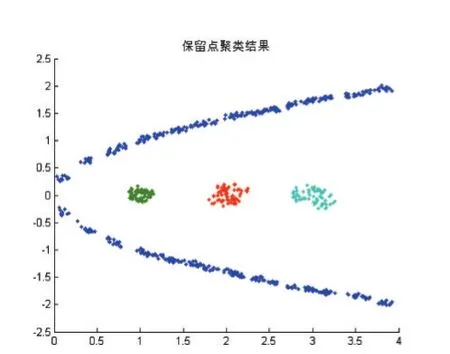
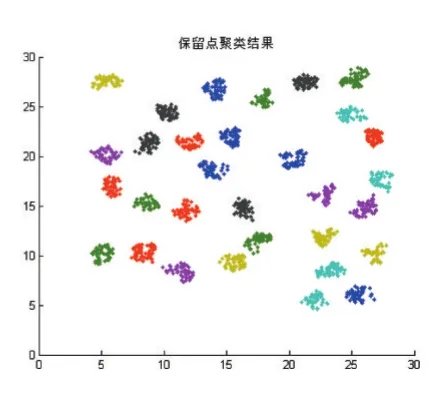
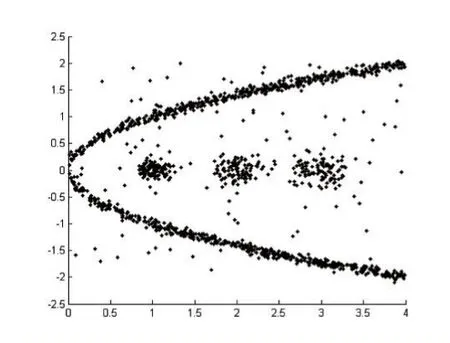
IfMaxDisti MaxDisti=dist Endif Endfor Endfor Foreachpiin Core 对Core创建 kdtree,找出Core中距离 pi小于 MaxDisti的点集合SpPoint ForeachpjinSpPoint dist=EuclideanDist(pi,pj) Ifdist Clusters(f ind(C lusters==Clusters(j) ))=Clusters(i) Endif Endfor Endfor 输出Clusters 核心点选择算法去除了几乎所有的噪声点和大部分簇边界点,因此还需要对被筛除的点进一步做归类,归类非核心点的思想是利用第一次对整个数据集使用的自然邻居算法得出的信息,计算非核心点的最大逆邻居距离,然后找出在该距离内的所有的核心点,接着判非核心点是否也在核心点最大逆邻居距离范围内,最后取距离最小的互在最大逆邻居范围内的保留点的类别为非核心点的类别,算法描述如下: 算法4:非核心点聚类算法 输入:核心点类别Clusters,核心点最大逆邻居距离MaxDisti,非核心点集合AddtPoint,非核心点自然邻居记录NNA,核心点集合Core,原始数据集D 输出:数据集D的聚类结果AllClusters 初始化N=num(D),AllClusters=zeros(1 ,N),AN=num(AddtPoint),AMaxDisti=0,AllClusters(Core)=Clusters ForeachpiinAddtPoint dist=0 ForeachpjinNNA(i) Ifdist dist=EuclideanDist(pi,pj) endif Endfor AMaxDisti=dist 对核心点创建kdtree,搜索在AMaxDisti范围内的所有核心点集合Set ClusterInd=0 MinDist=Infinity ForeachpjinSet dist=EuclideanDist( )pi,pj Ifdist MinDist=dist ClusterInd=Clusters(j) Endif Endfor IfClusterInd<>0 AllClusters()i=ClusterInd Endif Endfor 输出AllClusters 其中未被归类的点即被认为是噪声点。 表1前三列是实验所用到的数据集以及对应的类别数目: 表1 数据集和实验结果对比 这里以数据集Da6、d31为例子进行核心点选取和聚类,图1是Da6数据集的散点图,图2是d31数据集散点图。 图1 图2 使用算法2得到的核心点结果如下图,其中图3是Da6数据集的核心点散点图,图4是d31数据集的核心点散点图,可以看出核心点集合保留了整体数据集簇状结构,极大地弱化了簇边缘和噪声点的影响。 图3 图4 使用算法3得到的核心点聚类结果如下图,其中图5是Da6数据集核心点的聚类结果,图6是d31数据集核心点聚类结果。 使用算法4对非核心点进行归类结果如下图,其中图7是Da6数据集的聚类效果,图8是d31数据集聚类效果,其中“+”表示噪声点,结果中可以看出大量噪声点都被算法识别了出来。 表1后两列是NN-DBSCAN与DBSCAN算法在实验数据集上的聚类效果与正确率的对比,在circle2数据集上,两个算法都能取得最好的聚类效果,但是DBSCAN需要设定适当的邻域半径值和邻域阈值;由于db4和jain数据集样本数目较少,类别分布较为稀疏,核心点选取算法难以选取到合适的核心点;在d31数据集上,由于簇边界密度比簇内部密度相差太大,算法在聚类非核心点时便难以保证非核心点与同类核心点互在自身的邻域半径值内;综合聚类数目和正确率,NN-DBSCAN使用了自然邻居算法,自适应得到了核心点和邻域半径值,在消除人工设定参数的同时也保证了正确率。 本文提出了一种通过自然邻居算法改进的DBSCAN算法,聚类过程中首先筛除会干扰整体聚类效果的点,然后再用自然邻居算法对核心点进行处理,得到核心点之间的邻域关系,接着使用核心点的最大逆邻居距离替代了DBSCAN的邻域半径值ε,自适应的得到了每个点之间的邻域半径值,对原始DBSCAN算法中的邻域半径值参数进行分析,实际上是两个核心点的距离互在其对应的邻域半径之内,才能认定两个核心点属于同一个类别,基于该原理,算法聚类时选择了核心点之间的距离互在其最大逆邻居距离范围之内才认定两个核心点属于同一类别,通过实验也验证了该方法的有效性。 图5 图6 图7 图8 [1]孙吉贵,刘杰,赵连宇.聚类算法研究[J].软件学报,2008,19(1):48-61. [2]张莹.基于自然最近邻居的分类算法研究[D].重庆大学,2015. [3]程东东.基于自然邻的层次聚类算法研究[D].重庆大学,2016. [4]Ester M,Kriegel H,Jiirg S,et al.A Density Based Algorithm for Discovering Clusters in Large Spatial Databases[J],1996. [5]Ordering Points To Identify the Clustering Structure[C].International Conference on Management of Data,1999. [6]Li D F,Hu W C,He Y X.Classifier Based on Shared Nearest Neighbor Clustering and Fuzzy Set Theory[J].Control&Decision,2006,21(10):1103-1108. [7]Kaufman L,Rousseeuw P J.Finding Groups in Data.An Introduction to Cluster Analysis[J].Wiley,1990. [8]Kaufman L.Rousseeuw PJ:Finding Groups in Data:An Introduction to Cluster Analysis[J].Machine Design,1990,74. [9]Romesburg,Charles H.Cluster Analysis for Researchers[M].Lifetime Learning publications,1984. [10]Jain A K.Data Clustering:a Review[J].ACM Computing Surveys,2000,31(3):264-323. [11]周水庚,周傲英,曹晶,等.一种基于密度的快速聚类算法[J].计算机研究与发展,2000,37(11):1287-1292. [12]贺玲,吴玲达,蔡益朝.数据挖掘中的聚类算法综述[J].计算机应用研究,2007,24(1):10-13. [13]Jain A K,Dubes R C.Algorithms for Clustering Data[J].Technometrics,1988,32(2):227-229. [14]朱庆生,陈治,张程.基于自然邻居流形排序图像检索技术研究[J].计算机应用研究,2016,33(4):1265-1268. [15]段浪军.基于自然邻居和最小生成树的原型选择算法研究[J].计算机科学,2017,44(4):241-245.2.3 非核心点聚类算法
3 实验结果与分析
3.1 实验结果
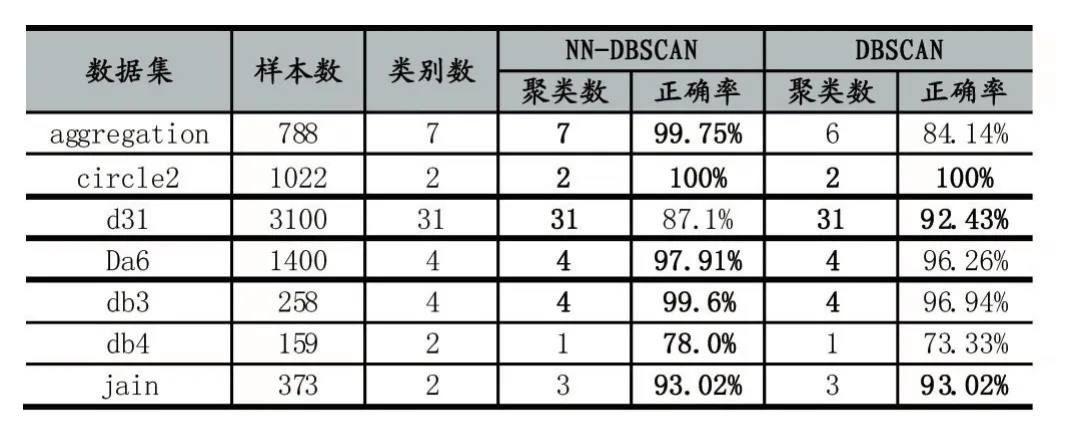
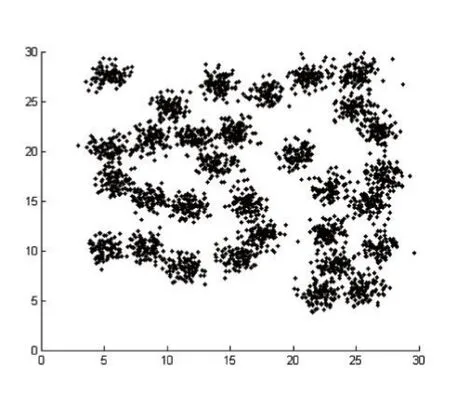
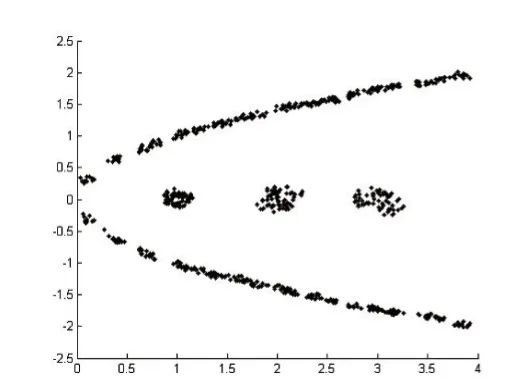
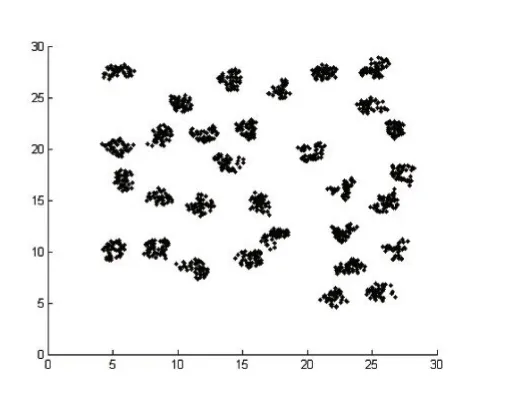
3.2 NNDBSCAN算法对数据集聚类性能
4 结语