关于微分多项式的零点

徐俊峰，叶水超



徐俊峰，叶水超

（五邑大学 数学与计算科学学院，广东 江门 529020）

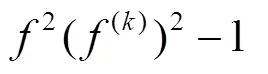
亚纯函数；微分多项式；值分布

1 引言与定理

本文使用Nevanlinna理论的符号，假设读者熟悉值分布的相关理论（详见参考文献[1]）.

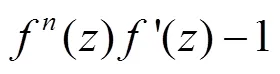
杨重骏在文献[10]中研究了整函数的情况，得到的结果如下：

K.W.Yu[11]证明了以下结果：

I.Lahiri和S.Dewan[12]推广了上述结果并给出了一个定量的结果：

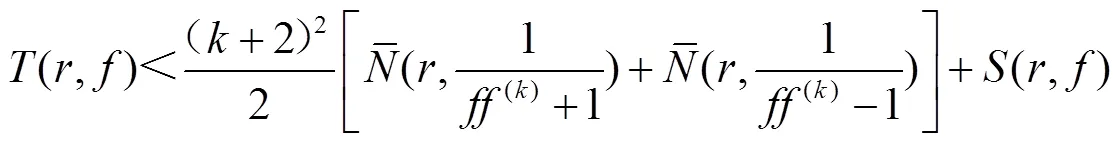
本文采用不同的办法改进了定理3的结果，得到一个定量描述：

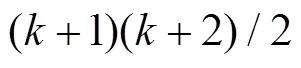
2 引理

我们的结果需要用下述的引理证明.

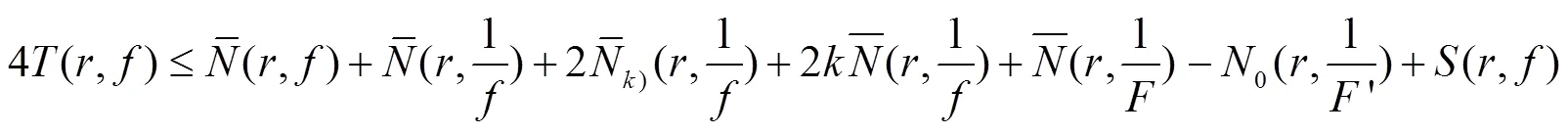
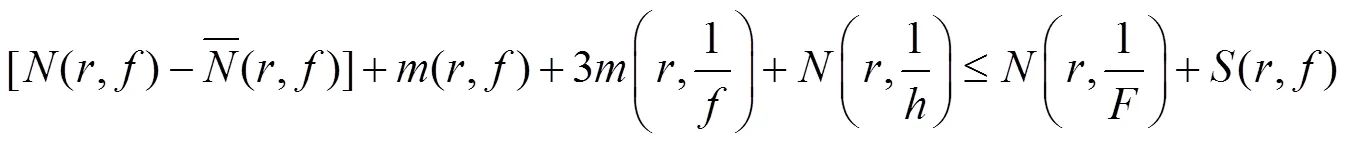
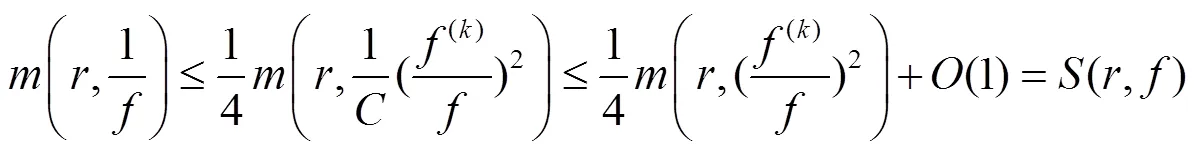
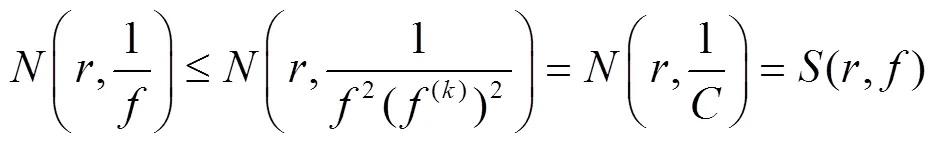
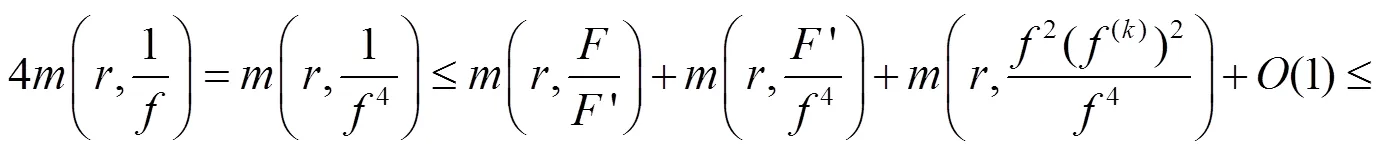
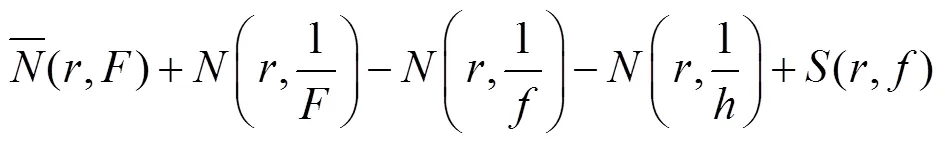
因而

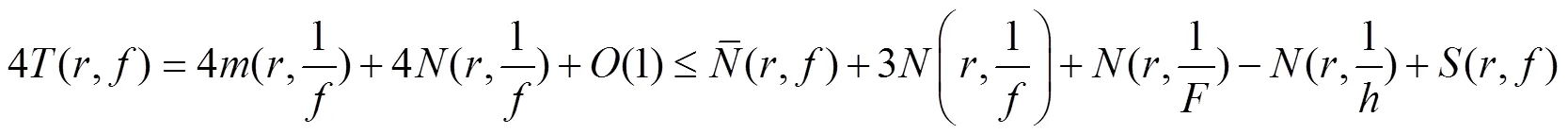
因为

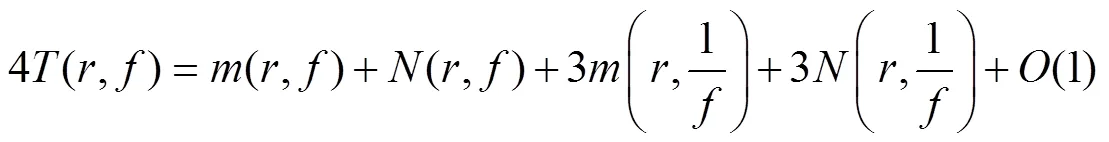
由式（4-5），得

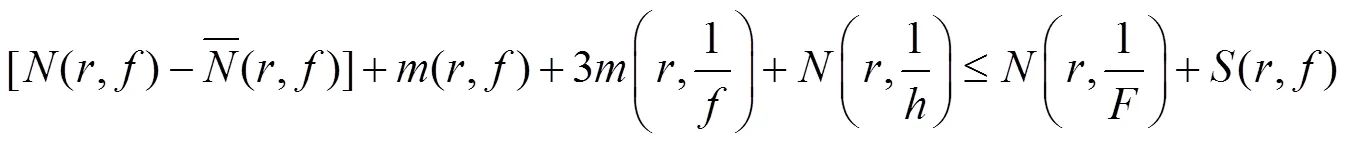
所以，不等式（2）得证.

设

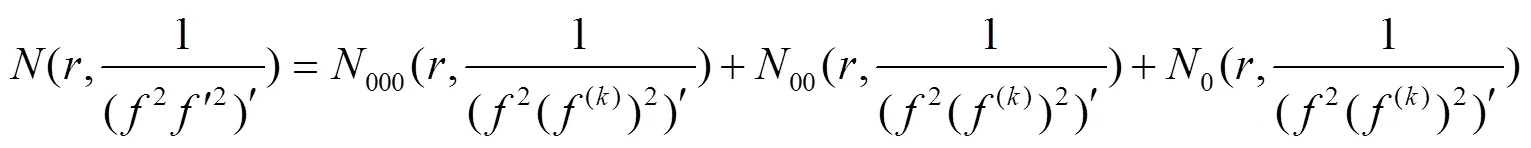
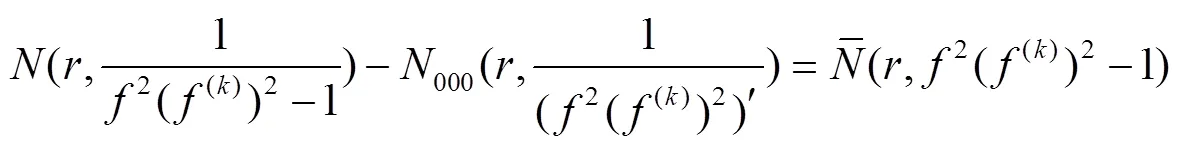
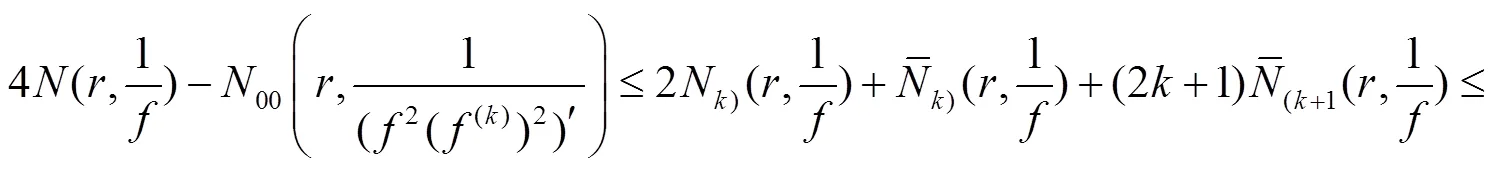
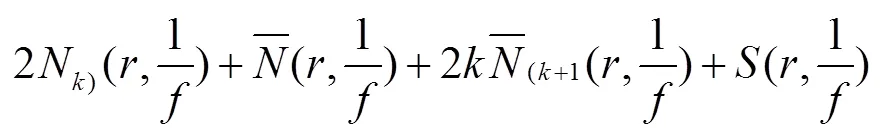
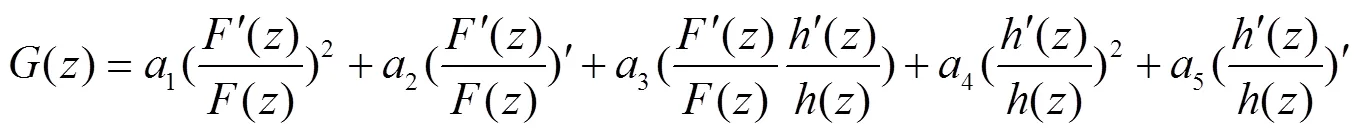
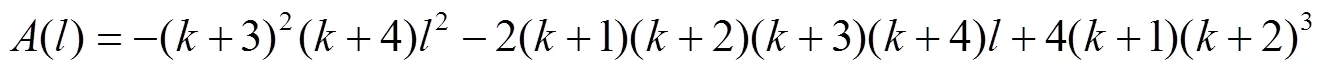
设

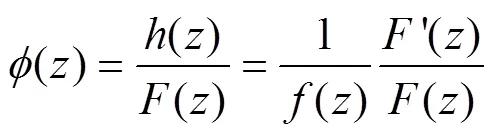
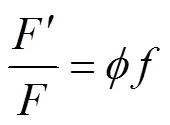
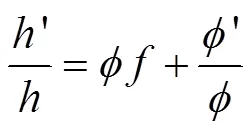
将式（11-12）代入式（9），得

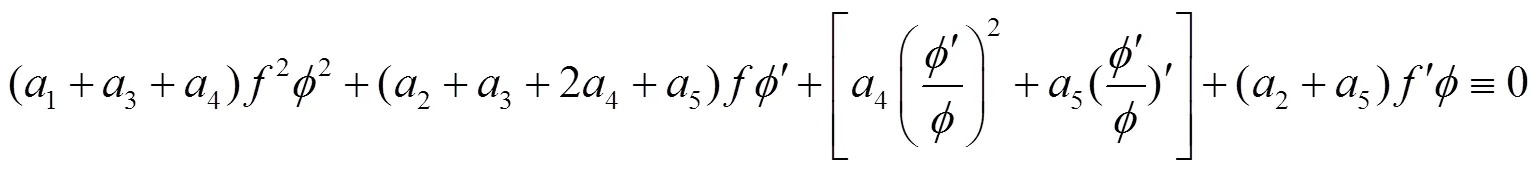
由式（13）得

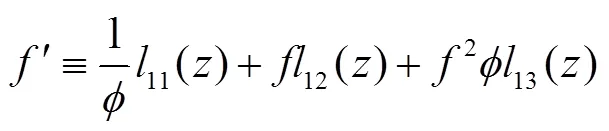
式（14）微分，得

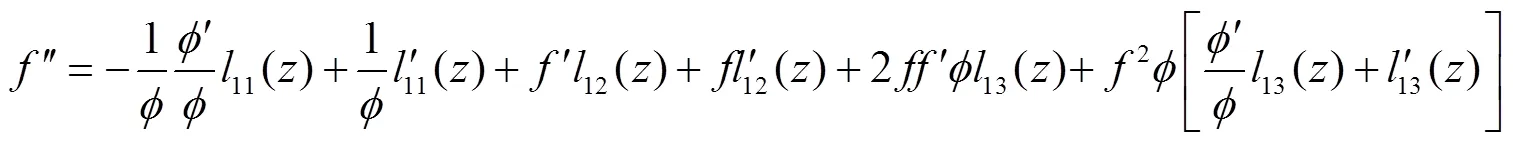
由式（14）和式（15）可得

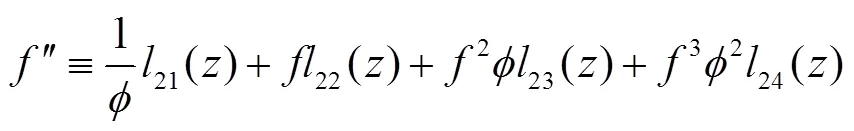
同理，可得

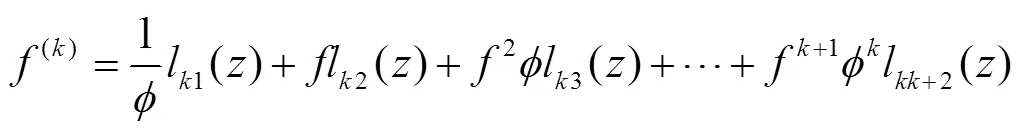
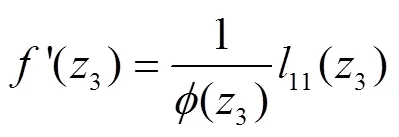
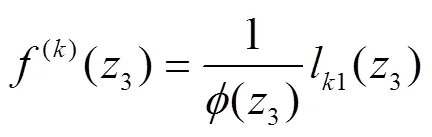
由式（18-19）和引理1，可得

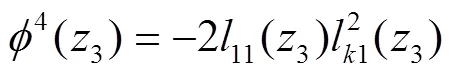
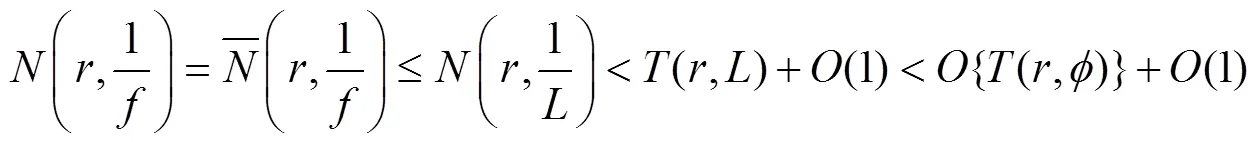
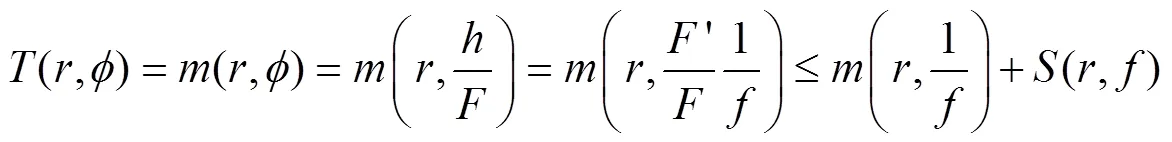
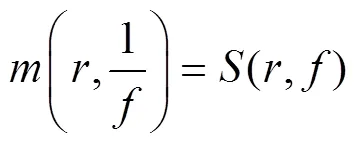
由式（21-23），得

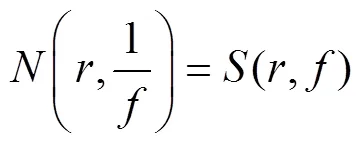
由式（23-24），得

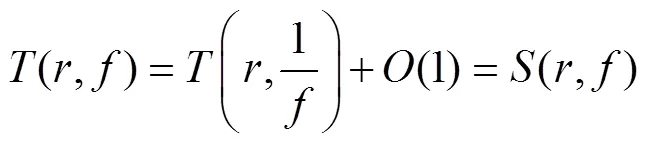
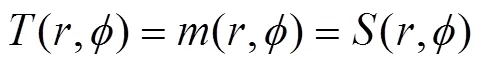
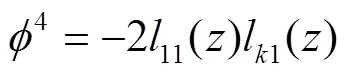
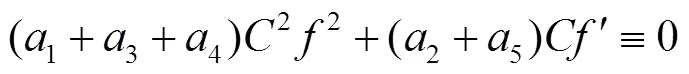
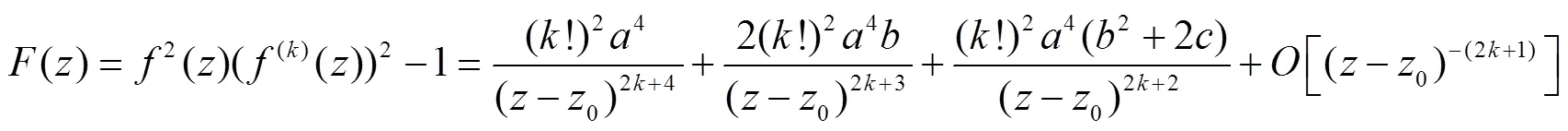
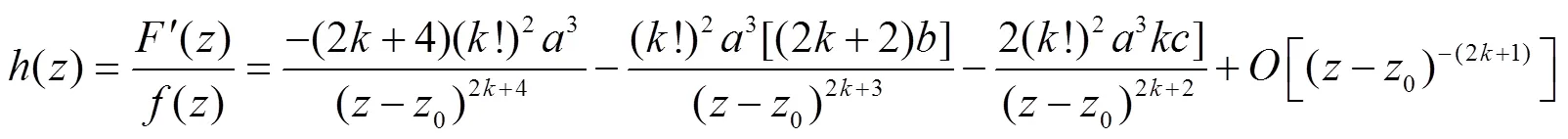
由此可得

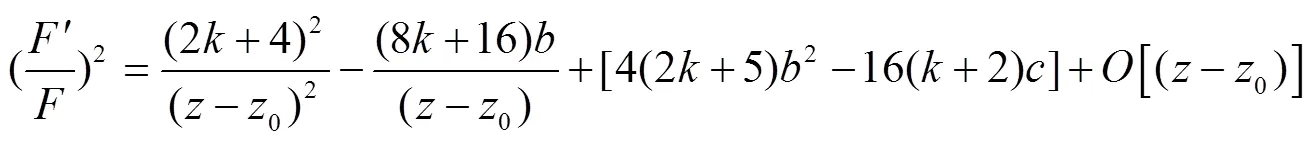
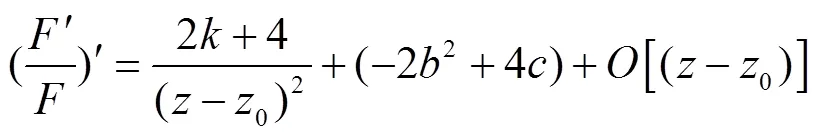
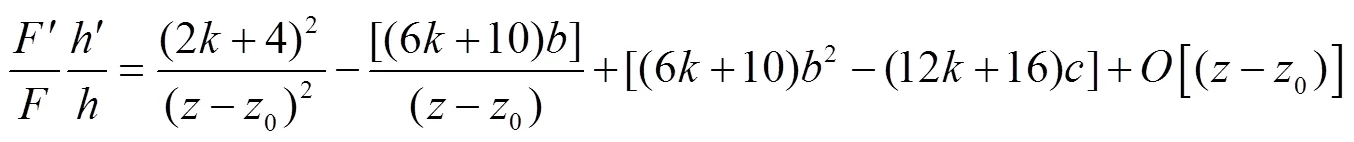
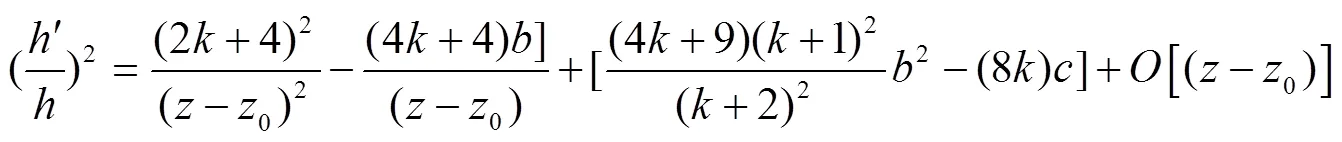
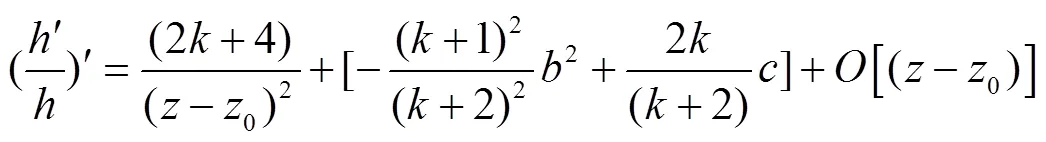
将式（29-33）代入式（9），得

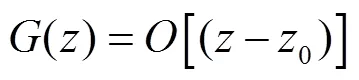
类似引理2的证明，我们可以得到如下结果：

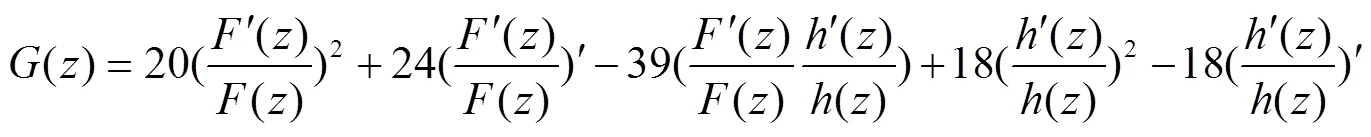
3 定理4的证明

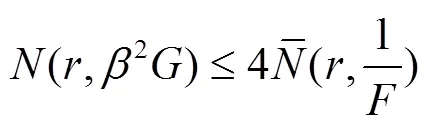
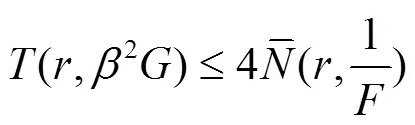
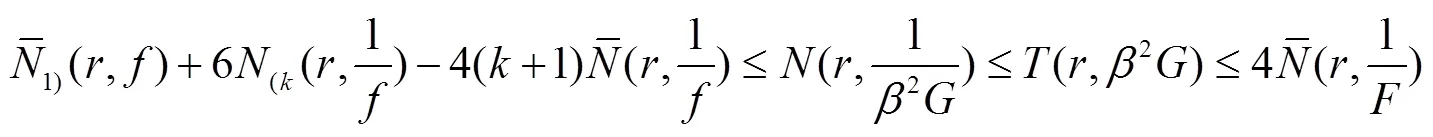
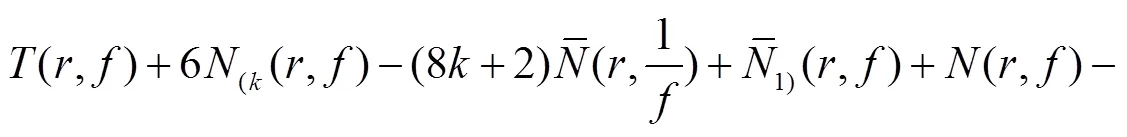
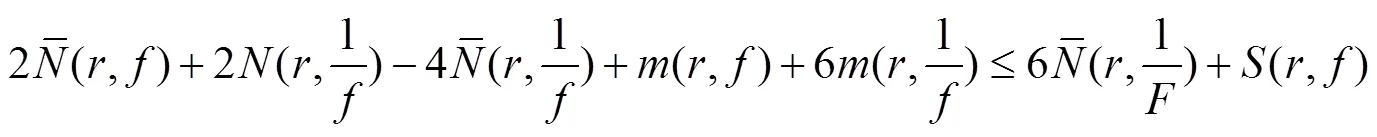
于是有

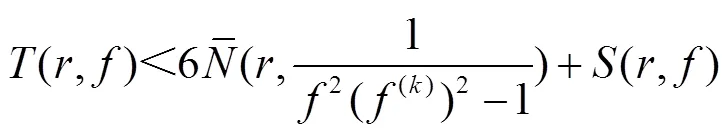
完成了定理4的证明.

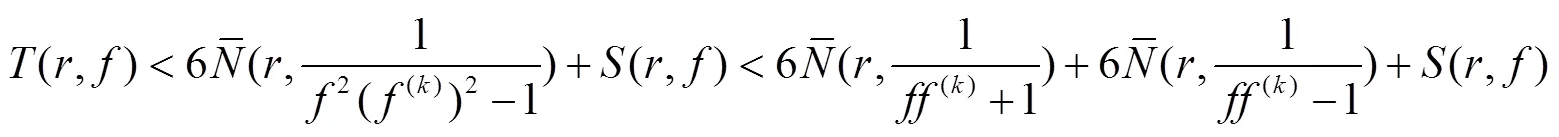
[1] HAYMAN W. Meromorphic functions [M]. Oxford: Clarendon Press, 1964.

[2] HAYMAN W. Picard values of meromorphic functions and their derivatives [J]. Ann of Math, 1959, 70(2): 9-42.

[3] HAYMAN W. Researcher problems in function theory [M]. London: The Athlone Press University of London, 1967.

[4]MUES E. Uber ein Problem von Hayman [J]. Math Z, 1979, 164(3): 239-259.

[5] BERGWEILER W, EREMENKO A. On the singularities of the inverse to a meromorphic function of finite order [J]. Rev Mat Iberoamericana, 1995, 11(2): 355-373.

[7]CLUNIE J. On integral and meromorphic functions [J]. J London Math Soc, 1962, 37(1): 17-27.

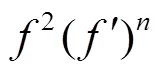
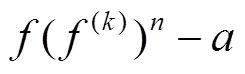
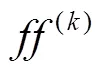
[11] YU Kitwing. A note on the product of meromorphic functions and its derivatives [J]. Kodai Math J, 2001, 24(3): 339-343.

[12] LAHIRI I, DEWAN S. Value distribution of the product of a meromorphic of and its derivative [J]. Kodai Math J, 2003, 26(4): 95-100.

[13] 戴瑞芳，徐俊峰. 一类微分多项式的零点的不等式估计[J]. 五邑大学学报（自然科学版），2017, 31(3): 1-7.

[责任编辑：熊玉涛]

XUJun-Feng, YEShui-Chao

(School of Mathematics and Computational Science, Wuyi University, Jiangmen 529020, China)

meromorphic functions; differential polynomials; value distribution

O189.1

A

1006-7302（2018）02-0001-07

2018-03-08

广东省自然科学基金资助项目（2016A030313002）；广东高校特色创新项目（2016KTSCX145）

徐俊峰（1979—），男，湖北南漳人，教授，博士，硕士生导师，研究方向为复分析及其应用.