两类双单叶函数类的不等式

郭栋



郭栋

（滁州职业技术学院 基础部，安徽 滁州 239000）

1 引言及预备知识

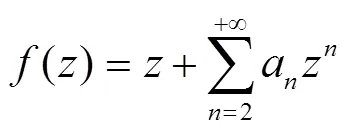
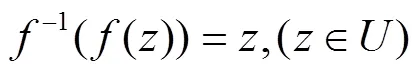
这里

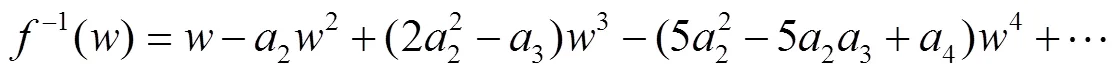
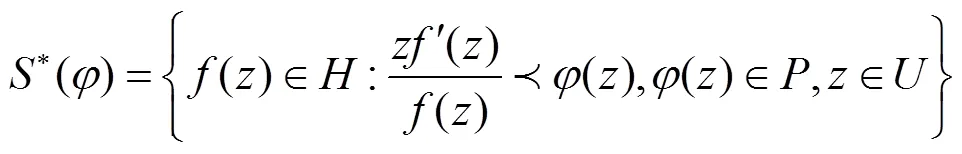
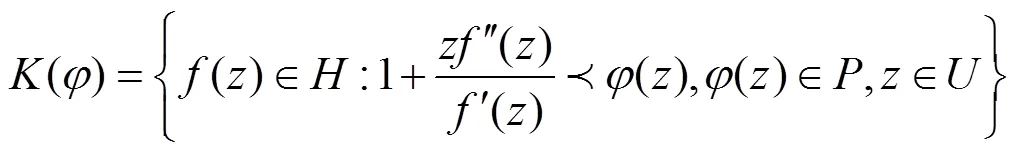
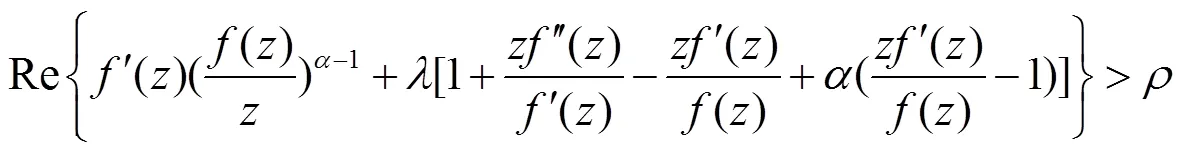
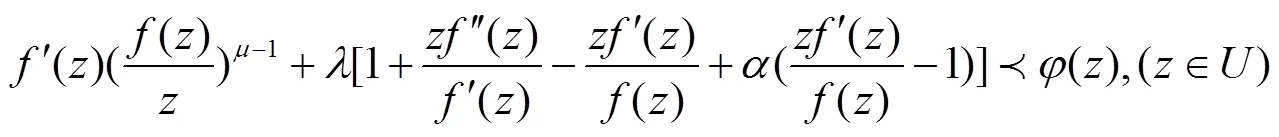
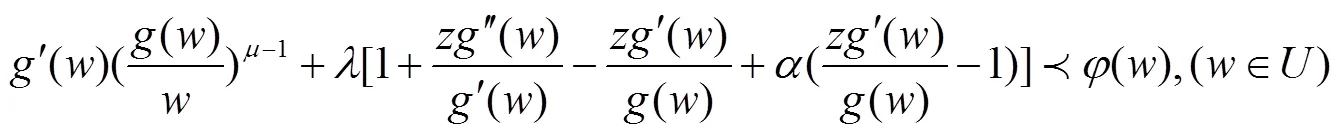
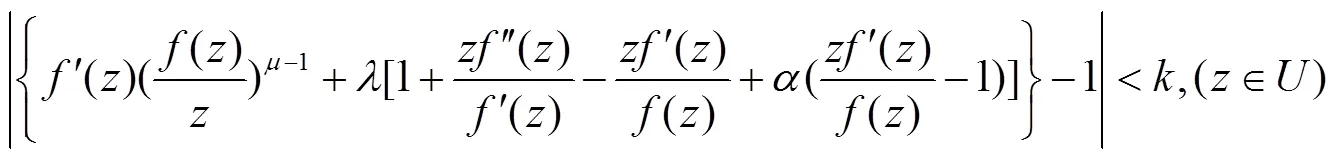
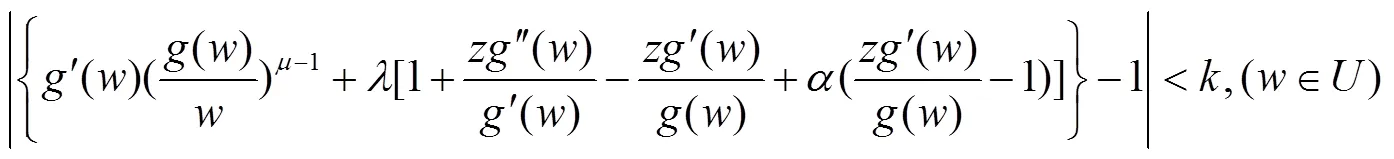
在定义1中令一些参数取一些特殊值，就得到我们熟知的双单叶函数类，例如：

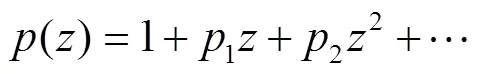
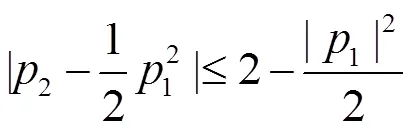
2 主要结果及证明

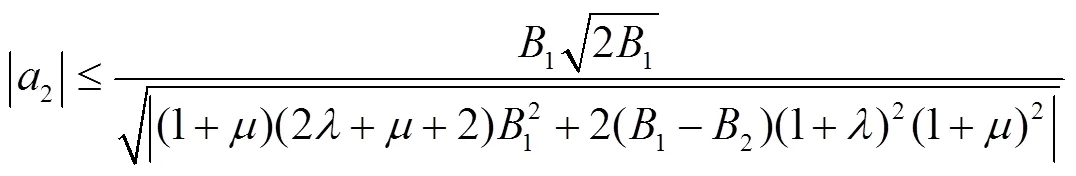
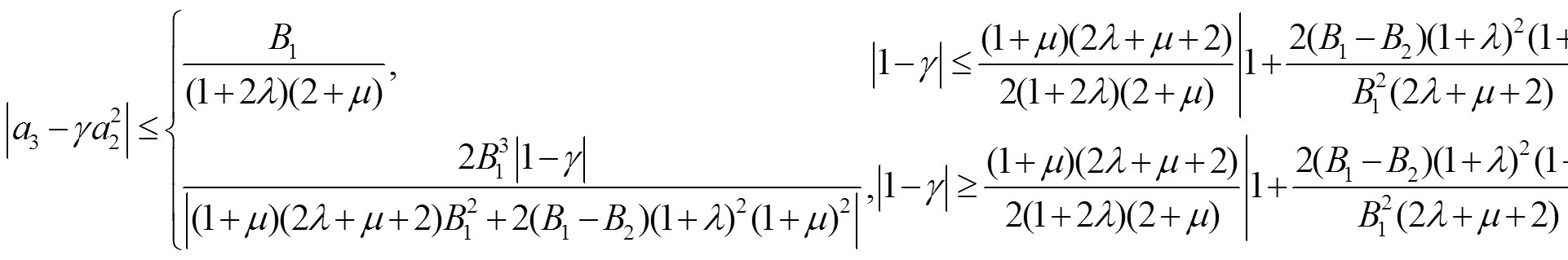
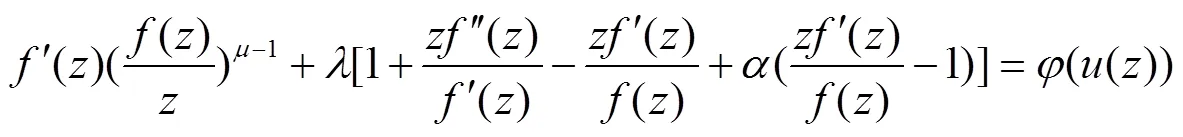
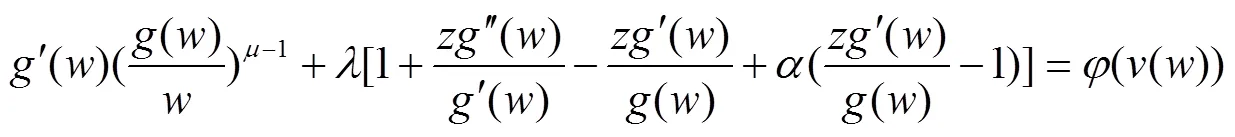
其中

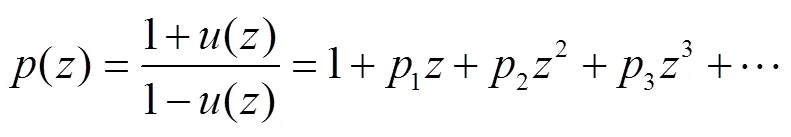
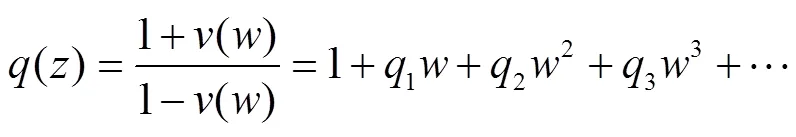
由式（7）和（8）得

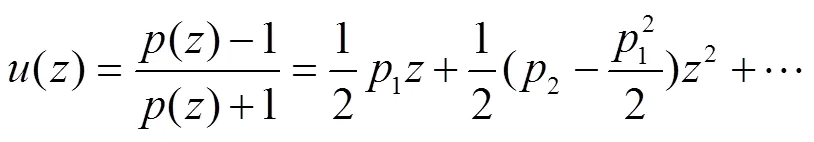
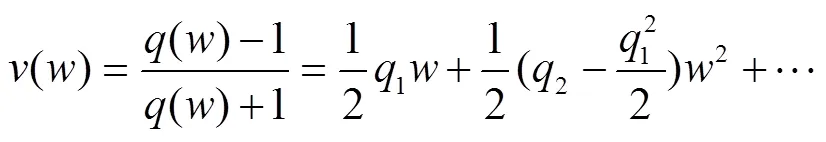
由式（5）、（6）、（9）和（10）得

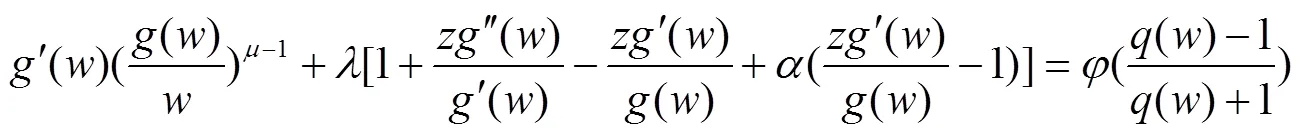
其中

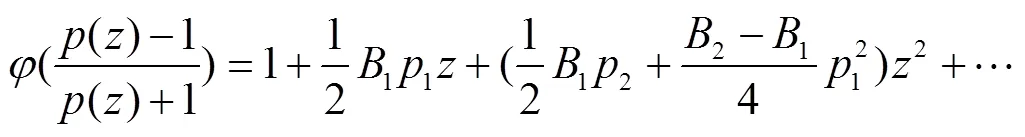
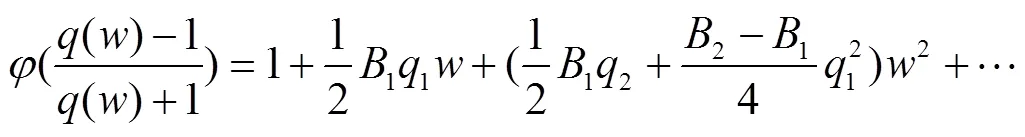
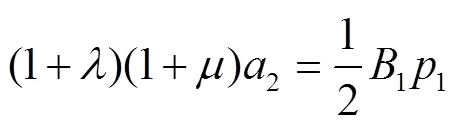
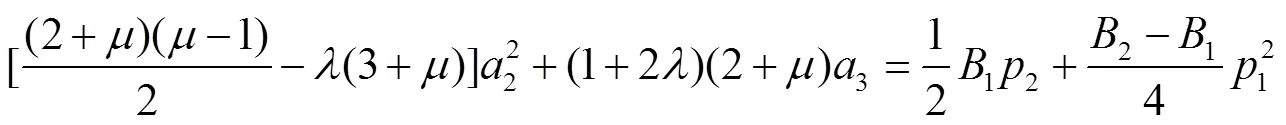
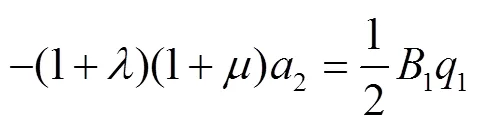
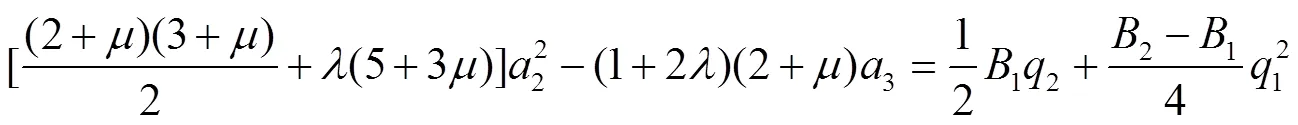
由式（13）和式（15），可得

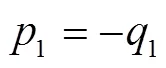
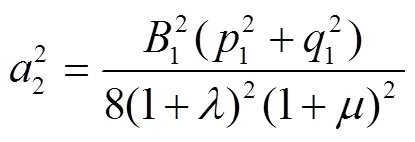
由式（14）和式（16），可得

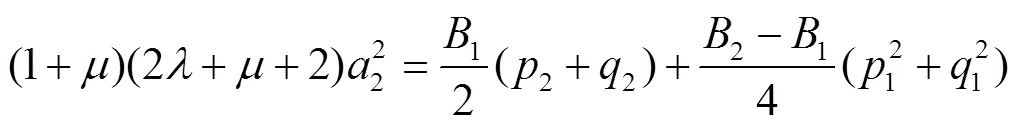
将式（17）、（18）代入式（19），化简得

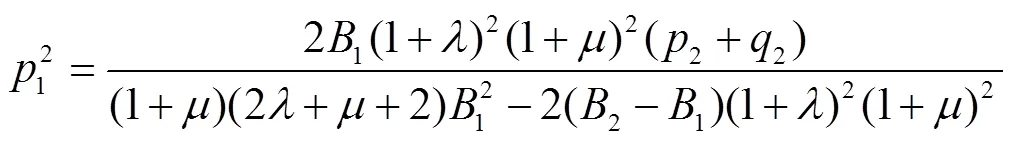
由式（17）、（18）和（20）可得

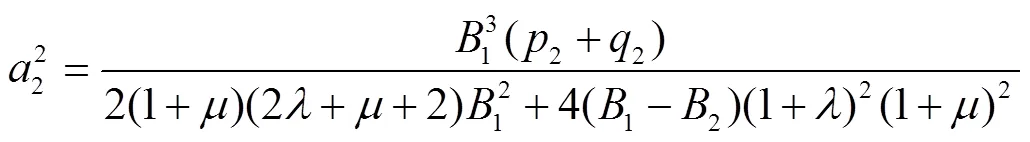
利用引理1及式（21），可得

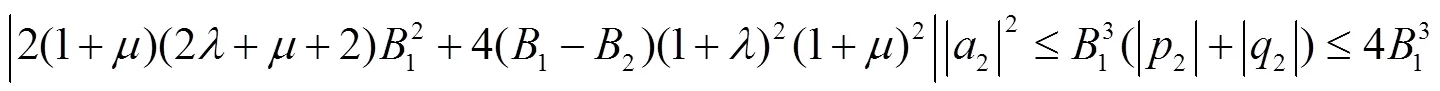
所以

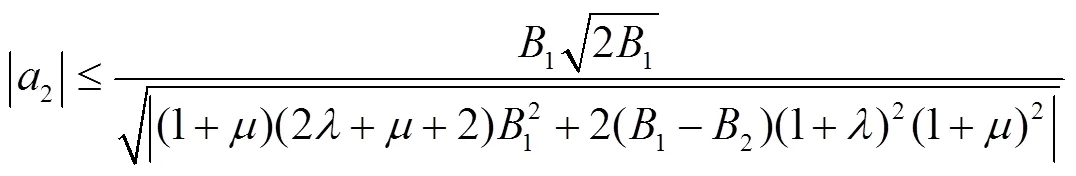
由式（14）、（16）和（17），可得

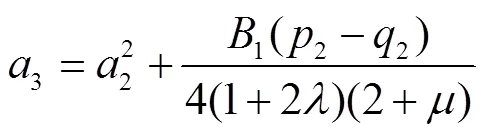
由式（21）和（22），可得

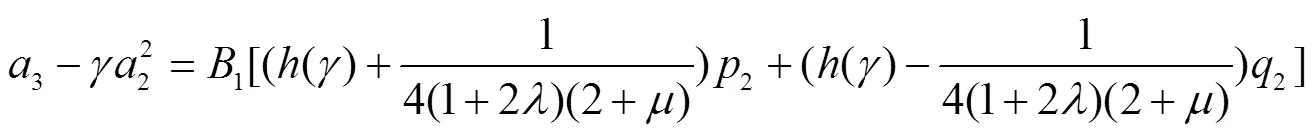
所以

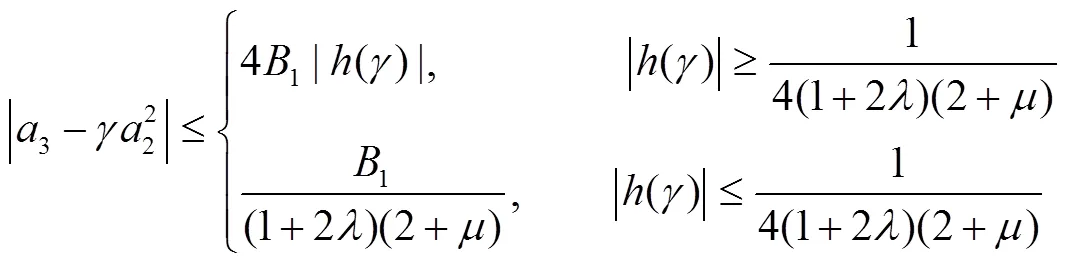
定理得证.

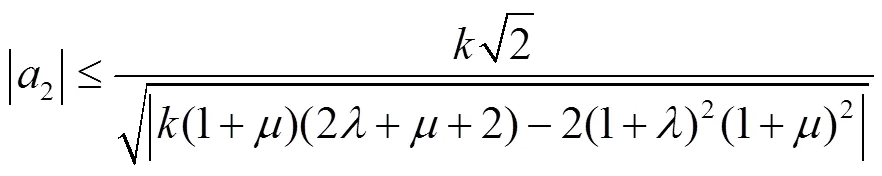
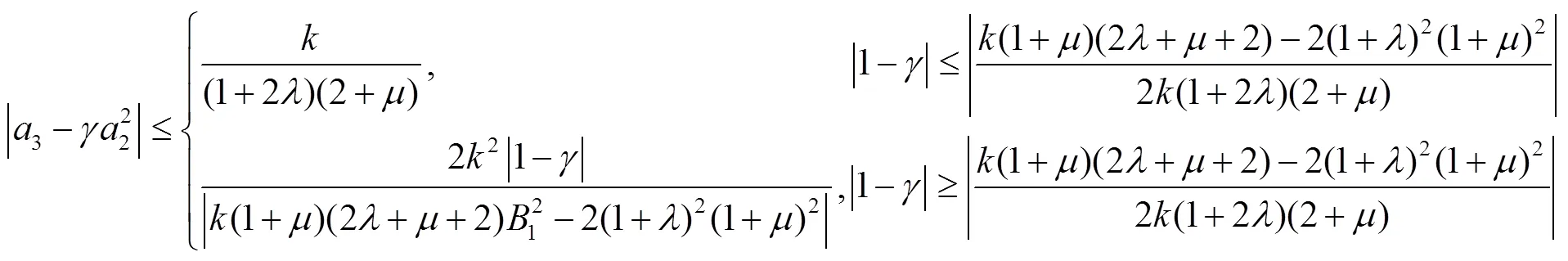
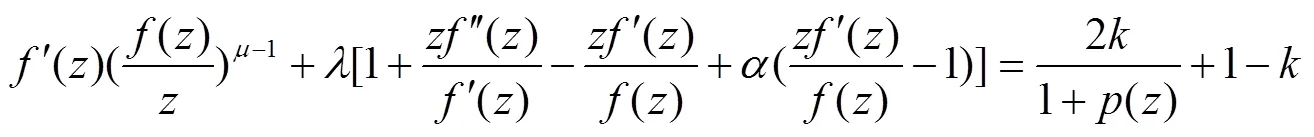
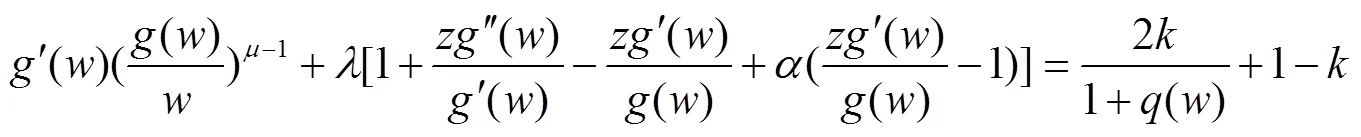
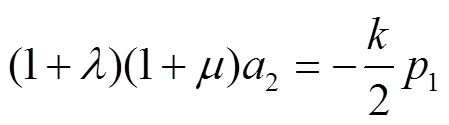
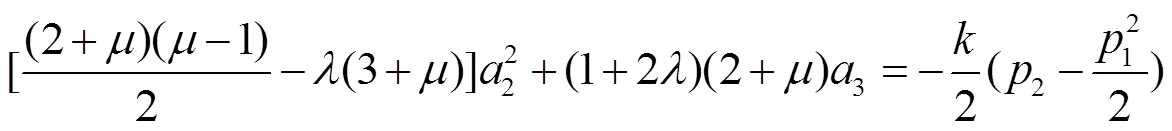
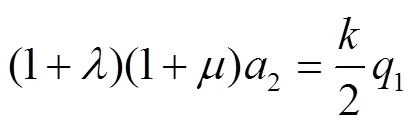
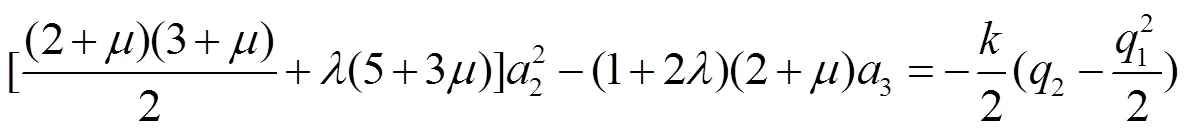
下面证明过程类似定理1.

3 主要推论及结果

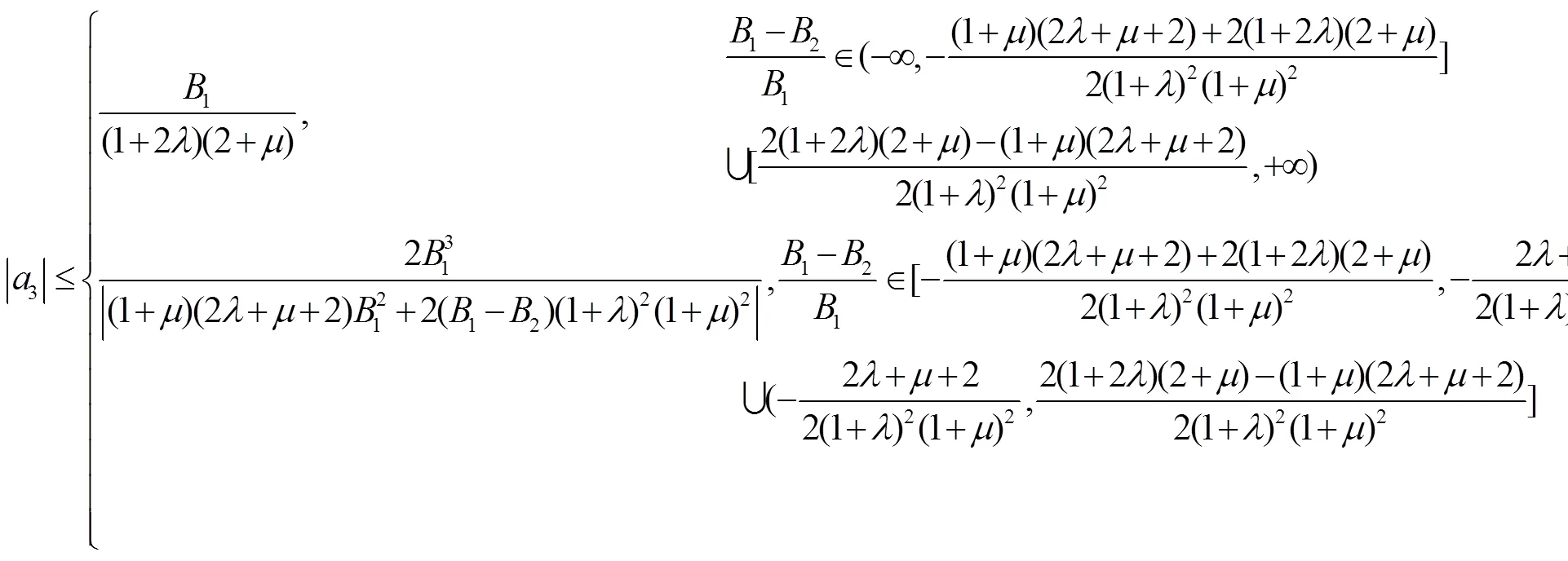
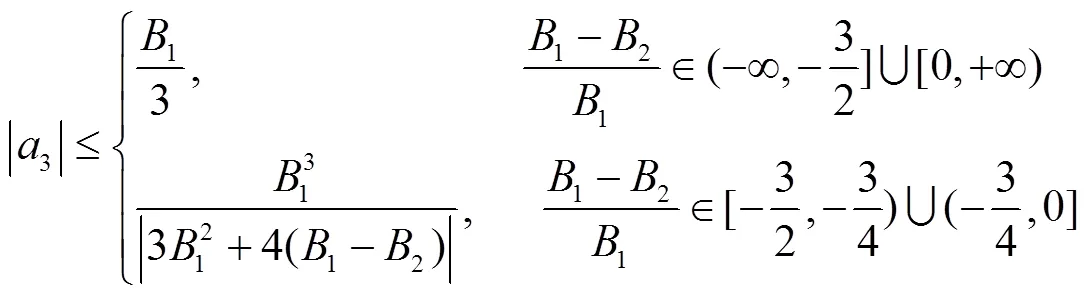
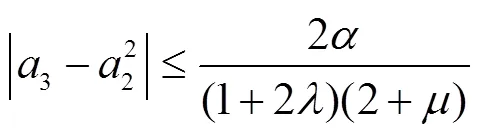
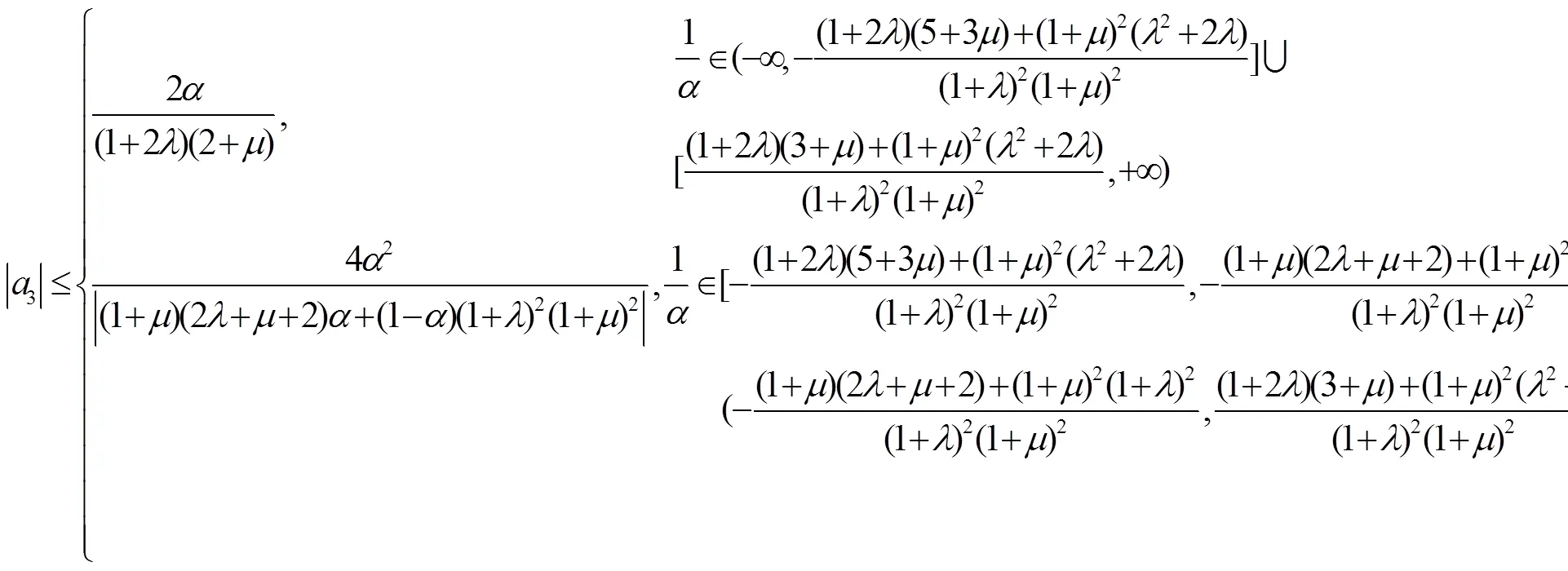
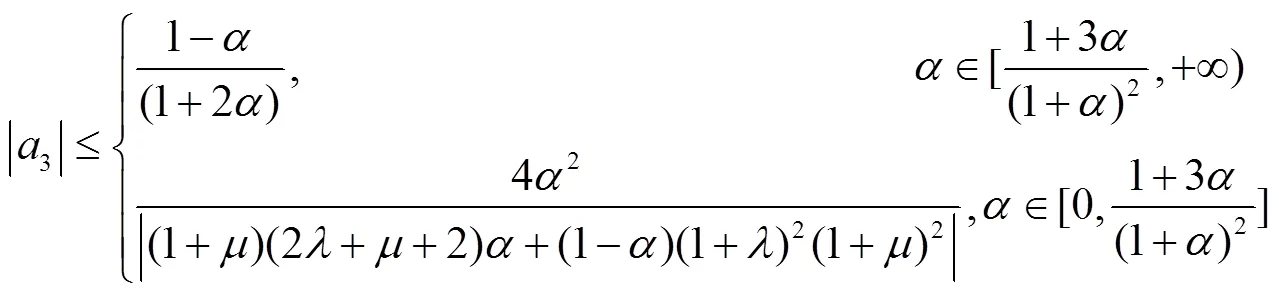
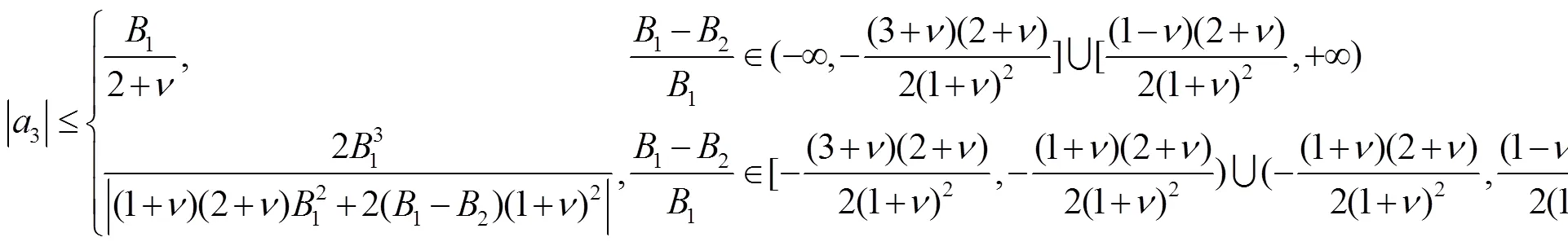
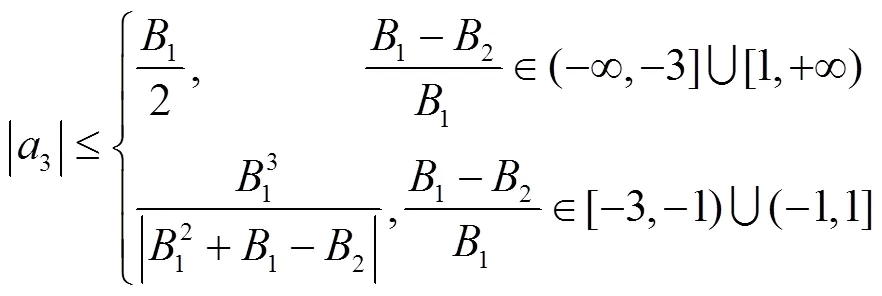
注释 推论8就是文献[11]中的推论3.7.

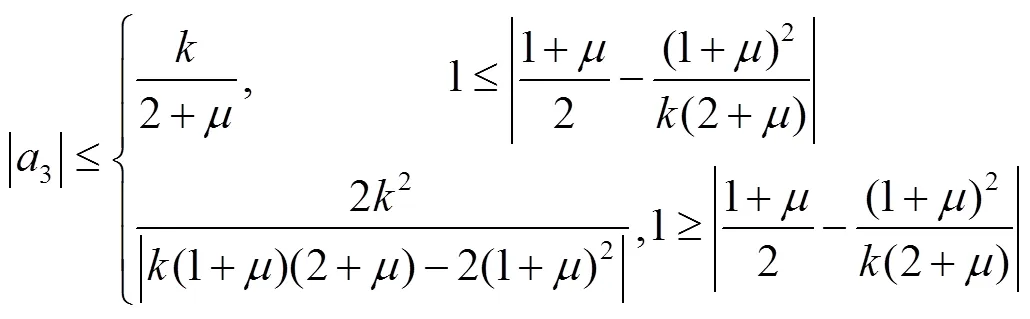
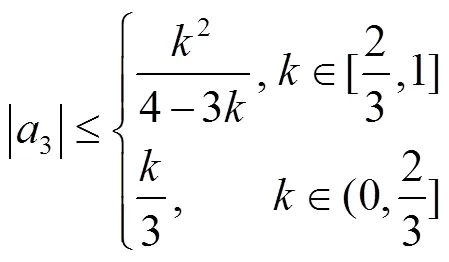
[1] LEWIN M. On a coefficient problem for bi-univalent functions [J]. Proc Am Math Soc, 1967, 18(1): 63-68.

[2] ALI R M, LEE S K, RAVICHANDRAN V, et al. Coefficient estimates for bi-univalent Ma-Minda starlike and convex functions [J]. Appl Math Lett, 2012, 25(3): 344-351.

[3] SRIVASTAVA H M, MISHRA A K, GOCHHAYAT P. Certain subclasses of analytic and bi-univalent functions [J]. Appl Math Lett, 2010, 23(10): 1188-1192.

[5] PENG Zhigang, HAN Qiuqiu. On the coefficients of several classes of bi-univalent functions [J]. Acta Math Scientia, 2014, 34B(1): 228-240.

[6] CAGLAR M, ORHAN H, YAGMUR N. Coefficient bounds for new subclasses of bi-univalent functions [J]. Filomat, 2013, 27(7): 1165-1171.

[9] GUO Dong, LIU Mingsheng. On certain subclass of bazilevic functions [J]. Journal of inequalities in pure and applied mathematics, 2007, 8(1): 1-11.

[10] POMMERENKE C H. Univalent functions [M]. Gottingen: Vandenhoeck and Ruprecht, 1975.

[责任编辑：韦 韬]

GUODong

(Foundations Department, Chuzhou Vocational and Technical College, Chuzhou 239000, China)

O174. 51

A

1006-7302（2018）02-0008-07

2017-12-09

安徽省高校自然科学基金重点资助项目（KJ2015A372，KJ2018A0833）.

郭栋（1976—），男，山东临沂人，副教授，硕士，主要研究方向为复分析及其应用.