高中数学教学实践中类比推理的应用

胡培强

(云南省武定县第一中学 651699)

类比推理在高中数学教学实践中的作用是是十分重要的，学生在学习过程中通过类比推理，能够获取解决问题的更好方式和新的思维.因为两种对象存在着一定的共同点是类比推理的前提条件，因此在解题过程中运用类比推理的关键在于对两类对象之间的联系，也就是共同点进行明确.

一、对概念范围进行拓宽

在教学过程中，我们掌握了已有的知识点，然后以掌握的知识点为基础，运用类比可以延伸出新的东西，通过对高中数学一些概念进行类比，能够发现新的定义.著名法国数学家伽罗瓦通过对乘法以及加法运算于不同的集合进行类比，引出了“群”这一新的概念.

例题1 有很多关系存在于我们所学的数学课题中，像是平行关系和相等关系，如果“～”是集合A中元素之间的一个关系，并且满足下面的几个条件：

1.传递性：对于a，b，c∈A，若a～b，b～c，则有a～c；

2.对称性：对于a，b∈A，若a～b，则有b～a；

3.自反性：对于任意a∈A，都有a～a.

那么，就将“～”称作为集合A中的等价关系.比如说“直线的平行”就不是等价关系，但是“数的相等”就是明确的等价关系.下面请根据题目中的说法，再整理出3个等价关系____.

结论：在例题1中的答案可以多很多个，比如说“命题的充分必要条件”、“图形的相似”以及“图形的全等”这些都可以是本题的答案.

二、运用升维类比，衍生新结论

高中数学立体几何章节，是整个高中数学教材中难度较大、内容较多的一个部分.在学习过程中为了掌握几何体的性质，通常情况下会在先整理曾经研究过的平面几何对象，然后通过类比推理掌握立体几何的性质，更容易去对性质进行猜想验证.比如说通过类比长方形去验证长方体，类比正三角形去验证正四面体等等.在对不等式的性质进行研究学习过程中，可以对维数较低的先进行研究，然后再去验证维数较高的不等式，比如说均值不等式等等.

例题2 (2014，山东理)2个正三角形在平面上的边长比是2∶1，那么他们的面积比就是4∶1，同理，2个正四面体在空间上的棱长比为2∶1，那么，请给出体积比____.

这道题的答案为8∶1.平面图形的面积通过类比的性质是相似比的平方;几何体体积比通过类比性质是相似比的平方.

三、运动降为类比，有效解题

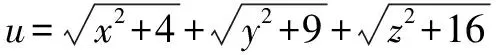
笔者将对本题的思考过程在下面列出来.

首先，在解答本题的过程中会联想到两点距离公示，但是下面的具体解题还不知道，紧接着类比2个变量的相似题目.

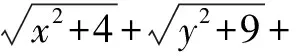
[当且仅当P(x,2),O(0,0),Q(y,3)三点在一条直线上时取等号]，即|PO|+|OQ|≥|PQ|.所以在对本题进行解答的过程中，要对5个点进行构造，分别是：

P(x,2),O(0,0),Q(y,3),R(x+y,2+3),S(z,4).

因此需要这样来解答这道题目：

结论：在这道题目中有2个比较重要的地方，也是难点所在.需要在解题的过程中对三角形不等式进行连续的2次构造，然后要对等高是怎样成立的，需要什么样的条件进行分析.在对三角形不等式进行构造过程中，存在较多的变量时，可以利用类比推理的方式适当地对变量的数量进行符合条件的减少.在对这道题进行解答过程中还需要注意一点，这道题目中等号如果想要成立，构造的3个点必须是在1条直线上.

高中数学教学内容复杂且多，这就要求学生能够运用类比推理的方法去解决和发现所学内容和将要学习内容的问题，比较晦涩的问题教师可以帮助解决，过程中要形成讨论，这样学生学习的知识才会更牢固，也有助于学生人之技能的形成.类比推理的重要性毋庸置疑，学生能够在此研究方法的帮助下获得问题解决的新方法和思路，学生的创新能力得到增强，主观能动性得到发展.教师在教学过程中要广泛地运用该方法，让学生对知识的掌握进行类比推理，发现并解决所遇到的问题.

参考文献：

[1]杜长固.类比推理在高中数学教学实践中的应用研究 [J].中国校外教育，2013(34).

[2]庞东.高中数学教学中类比推理法的有效实施 [J].基础教育研究，2014(9).

[3]于波.类比推理在高中数学教学中的应用 [J].中国校外教育，2014(4).