把握小题 智慧大做

孙瑛

习题是小学数学教学的重要组成部分，是学生掌握知识、形成技能、获取数学活动经验和数学思想方法的重要平台。在实际教学中，教师要对习题进行深入的解读、挖掘和再创造，充分发挥习题的价值。

选题缘起

圆柱的学习已经有好几个课时，学生对圆柱的特征有了充分的认识，对于圆柱侧面积、表面积的计算也比较熟练。但是，我总感觉还需要补充拓展有关表面积变化的知识，加强学生对图形空间的探索与思考，提高解决实际问题的能力。如往常一样，我在备课时认真做起了书上的习题。当我用铅笔快速连完练习三的第4题（如下图所示），一个念头闪过脑海，何不就以此题为切入口，来一次小题大做？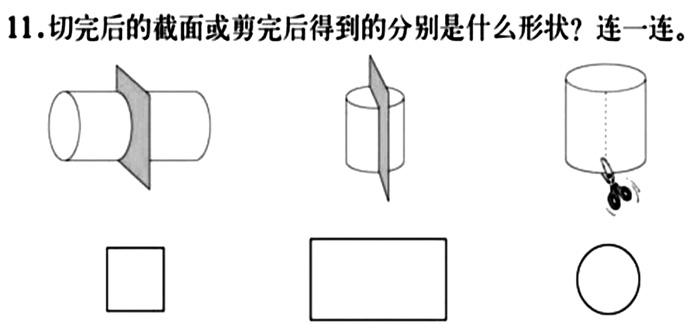

选题分析

一、从解题思路入手

1.审题，读懂题目中文字信息的要求。

学生图文结合认真审题，抓住题目中的关键词“剪”和“切”。

（1）判断切后截面的形状。

（2）判断剪后侧面展開的形状。

2.审题读图，挖掘隐藏的信息。

（1）第一个圆柱，是判断平行于底面切后的截面的形状。

（2）第二个圆柱，是判断垂直于底面切后的截面的形状。

（3）第三个圆柱，是判断沿着侧面的一条高剪开后侧面展开的形状。

二、思考解决方法

1.小组合作，实物操作

（1）将一个圆柱沿平行于底面切后的截面，是与圆柱的底面大小相等的圆。

（2）将一个圆柱垂直于底面切后的截面，一般是长方形，圆柱的底面直径与高分别为长方形的长与宽；当底面圆的直径与圆柱的高相等时，截面会是一个正方形。

（3）将一个圆柱的侧面沿着一条高剪开，会得到一个长方形。

对圆柱侧面展开形状的研究，会在求圆柱的侧面积时有重点地交流探讨，所以这里的重点可以放在切这个方面。

2.同桌协助，模拟感悟

（1）一生将左右手握紧拳头，合并形成“拳头圆柱”，另一生则用手掌模拟切的动作。当两个拳头分开时，学生感悟：一个圆柱平行于底面切后的截面，是与圆柱的底面大小相等的圆。

（2）一生将左右手半握拳合拢形成“拳头圆柱”，直观感受大拇指的长度相当于圆柱的底面直径，另一生则用手掌模拟切的动作。当两个拳头分开时，学生感悟：一个圆柱垂直于底面切后的截面是长方形，圆柱的底面圆直径与高分别为长方形的长与宽；当底面圆的直径与圆柱的高相等时，截面是一个正方形。

（3）一生握紧一个拳头，再展开，感受：将一个圆柱侧面沿着一条高剪开，会得到一个长方形。

3.凭借经验，空间想象

（1）最有把握的是第一个圆柱，平行于底面切后的截面是圆。

（2）第三个圆柱的底面周长比圆柱的高长一些，侧面沿着一条高剪开得到的会是一个长方形。

（3）最后分析第二个圆柱的截面应该是正方形。三、探求拓展路径

1.关于2号图的拓展

学生读题后感悟，沿底面直径将圆柱锯成两块，是刚才题中的第几号图的切法。因为有前面切法的引导，所以学生会轻松地得出“增加两个长方形面积”的结论，找准长与宽的数据，得到答案。

2.关于1号图的拓展

（1）这会是几号图切法———1号图。学生感受到平行于底面切1刀，就会截成两段。两个小圆柱表面积的和比原来增加两个底面面积。归纳整理：平行于底面切n刀，就会增加2n个底面面积。

（2）引领学生借助“拳头圆柱”感悟：切掉一截，原来的上底面———在，原来的下底面———也在，原来的侧面积———少了。

总结：圆柱截下一段，表面积会减少，减少的就是截掉的这一截圆柱的侧面积。

（3）类比推理：圆柱增高一段，表面积会增加，增加的就是增加的这一截圆柱的侧面积。

（4）出示拓展题：

①一个圆柱，高减少2厘米，表面积就减少50.24平方厘米，上面的小圆柱，侧面积就是50.24平方厘米。

②一个圆柱，高增加3厘米，表面积就增加18.84平方厘米，上面的小圆柱，侧面积就是18.84平方厘米。

反思：教师个人应该养成深入研究习题的习惯，教师团队应该形成智慧研讨习题的氛围，提升讲题技能，这样才能更有的放矢地把控数学课堂，游刃有余地引领学生的思维，使之能举一反三、触类旁通，从而让数学课堂绽放不一样的精彩。

（作者单位：长沙市雨花区砂子塘小学）