风力载荷对实船参数横摇预报的影响研究

周耀华 ，马 宁 ， 尹晓辉 ， 鲁 江 ，石 珣

（1.中国船级社上海规范研究所，上海 200135；2.上海交通大学海洋工程国家重点实验室，上海 200240；3.中国船舶及海洋工程设计研究院，上海 200011；4.喷水推进技术重点实验室，上海 200011；5.中国船舶科学研究中心，江苏 无锡 214082）

0 引 言

自APL CHINA号在北太平洋遭遇了严重的参数横摇事故[1]以来，集装箱船的参数横摇现象引起了海事界的高度关注。由于该现象能够引起船舶的大幅横摇，故而作为一种严重危害船舶安全的重要稳性失效模式，已被国际海事组织（IMO）纳入了研究范围，并取得了部分研究成果[2-7]。

船舶的实际航行经验表明，即便迎浪航行，也有可能长时间承受斜风载荷的作用。由于前人的研究多侧重于迎浪或随浪航行时的参数横摇响应，因此风力载荷的影响多被忽略。近年来，风浪联合作用的水动力学问题逐渐引起了一些学者的关注。Bulian[8]对于风浪联合作用下的横摇运动预报开展了工作，考虑了平均风速和阵风的作用，风力谱基于Davenport谱。Chang[9]在参数横摇的研究中，对顶浪、随浪和斜浪的情况均进行了计算，其运动模型基于Blendermann的方法，对横摇自由度考虑了风力载荷的作用，并取得了有意义的成果。本文在前人的基础上，通过对3艘集装箱船和1艘散货船在规则波作用下的参数横摇敏感性计算，基于弱非线模型研究了风力载荷假定对实船参数横摇预报结果的影响。

1 风浪联合作用的数值模型

1.1 风载荷假定

大型集装箱船由于甲板上装载集装箱，水线以上侧投影面积与风倾力臂之积通常较大，因此恶劣气象条件下承受的风倾力矩将会十分可观。在CMV CCNI GUAYAS事故[7]期间，风向和浪向在较长时间内存在明显差异。这表明在实际海况下，即使船舶迎浪航行也有可能会承受风载荷引起的横摇力矩。

本文的研究假定船舶迎浪航行时遭遇侧风，此时船舶受到侧风横向分量引起的横倾力矩激励。风力载荷假定为随时间改变的风倾力矩。根据风的类型、平均风速、地理区域和地形等多种因素，风力谱可假定为多种型式[8]，本文对时变风速的计算采用Davenport谱：

其中为平均风速和时历风速变化项；AL为船侧面受风面积；Hc为风倾力臂，取从侧受风面积中心至平均吃水1/2处的垂直距离；Cm为空气阻力系数。

现代集装箱船出于营运需求对于航线和时间安排十分紧凑，遭遇恶劣海况的概率较高。本文中平均风速Uw参照2008年国际完整稳性规则（2008 ISCode）假定为26 m/s。平均风速的取值是IMO根据166个海难报告的气象条件统计后选取的，参与统计的绝大多数海难发生于蒲氏风级4至10级的恶劣海况下。对于空气阻力系数Cm，可以采用风洞试验测量。本文参照2008 ISCode对于若干实船风洞试验结果综合后的取值，假定为1.22。该系数已经考虑了风倾力臂定义的影响。

1.2 风浪联合作用的参数横摇数值模型

对于参数横摇的预报，势流理论以及非线性力学的方法得到了广泛应用。国际上主要有欧盟资助的SAFEDOR项目和ITTC波浪中稳性委员会主导的研究项目以及日本学者Umeda等人[11]的研究工作，并取得了丰硕的成果[12-14]。国内的杨素军，范余明[15]，付丽坤，蒋志鹏[16]，常永全，范菊[17]，唐友刚，邝艳香，李红霞[18]，鲁江[19]，陈京普[20]等学者也开展了深入的研究。

本文采用的运动预报模型基于典型的弱非线性三自由度模型[2]。此类考虑时延效应和F-K力非线性的弱非线性方法已在对参数横摇的研究中得到过成功应用[11，17]。运动方程见下式：

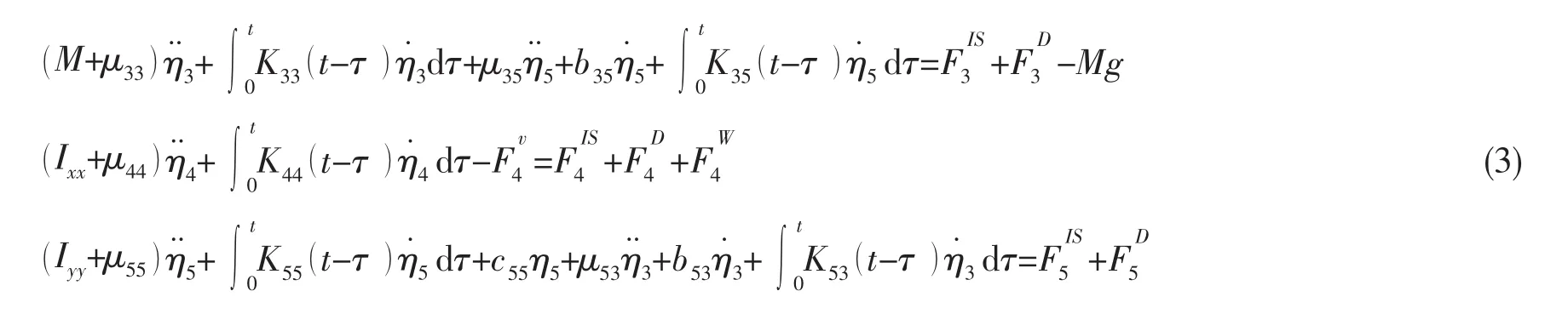
式中为根据1.1节中假定简化后的侧风横向分量引起的时变横倾力矩（见（1）式）。假定航速在风阻和波浪增阻综合作用下趋于稳定，仅考虑垂荡、横摇和纵摇的耦合运动。F-K力和回复力的合力的计算基于三维压力积分方法，且考虑了由于船体瞬时湿表面积所引起的非线性效应。辐射力和绕射力FD的计算基于三维频域线性水动力方法。其中辐射力的计算基于脉冲响应函数理论，以考虑时延效应：

式中：）为频域理论计算的兴波阻尼。粘性效应简化为横摇粘性阻尼力矩，可采用横摇衰减试验结果或Ikeda方法[21]估算。μjk为通过在平均湿表面下求解三维边值问题得到的附加质量和附加惯性矩，计算表达式及定解问题如下：

构造积分方程，采用三维方法计算。积分方程为：

其中

首先采用C11集装箱船模型在波长船长比为1.0、不同波陡下的试验结果[19]对本文的计算模型进行验证计算。粘性横摇阻尼基于试验数据。

参数横摇对于横摇惯性矩和GM值具有极高的敏感性，而通过模型试验无法高精度的测量模型惯性矩，因此为了尽量消除惯性矩对数值模型精度验证的影响，对于C11船模横摇惯性矩采用了如下方式计算：

首先采用近似公式，根据试验测定的横摇固有周期估算横摇惯性矩。

其中：IXX为船舶横摇惯性矩为船舶质量（kg）；g为重力加速度；GM 为初稳性高度（m）；T为横摇固有周期（s）；附加惯性矩△IXX采用三维势流理论计算得出。

然后以（8）式结果为初始值，采用粘流CFD求解器ISIS-CFD通过模拟船模静水横摇衰减计算船模横摇固有周期。依据比较横摇固有周期计算值与船模试验结果的误差，迭代确定横摇惯性矩的取值。该方法曾成功应用于对安装有附体的军船模型的横摇衰减模拟，取得了良好的结果[22]。图1给出了采用初值迭代计算过程中，横摇惯性矩取值对应的横摇固有周期误差结果。由图1可见，初始估算值对应的固有周期误差较大，而迭代收敛点的误差已由初始的5.3%降至-0.1%。C11验证计算采用惯性矩最终迭代结果。

参数横摇现象发生时的横摇和纵摇的时历运动响应表明（见图2），横摇周期近似为纵摇周期的两倍，即所谓的2：1响应。F-K力和恢复力的计算结果也表现出一定的非线性效应。图3给出了不同入射波陡时数值计算结果与试验结果的比较。

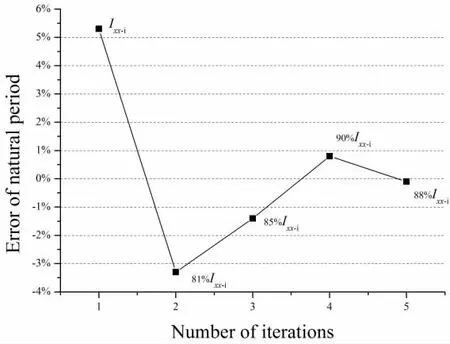
图1 惯性矩迭代过程对应的横摇固有周期误差Fig.1 Error of natural roll period during iteration

图2 C11船模参数横摇运动响应模拟及F-K力时历Fig.2 Simulations of parametric roll of C11 and the time-history of F-K force

实船事故的经验表明[1]，当船舶稳定地发生较大幅值的参数横摇时，船舶、货物及人员的安全受到了严重威胁。因此对于实船工程预报而言，能否准确预报发生大幅参数横摇现象，特别是提高横摇幅值安全临界点附近的预报精度对于船舶安全性评估具有重要工程意义。目前IMO倾向于采用满足适度精度且相对简化的模型[23]用于工程实践，并暂时将横摇幅值25°作为判断是否发生威胁船舶安全的参数横摇现象的安全临界点。若假定25°横摇角作为可能威胁船舶安全的标准值判断，则采用本文的数值模型针对C11船模的成功预报概率为91.67%，虚警率为8.33%，而预报失败率为0.0%。因此针对C11模型个案的分析表明，本文采用的三自由度运动模拟方法在安全临界点附近满足适度的预报精度，能够较为准确地对船舶动稳性安全性进行评估。由于参数横摇的非线性特征，采用相对简化的弱非线性模型必然在数值模拟精度上有所牺牲。该数值模型辐射、绕射力的模拟未能考虑非线性影响，横摇粘性阻尼的计算也是基于船模静水横摇试验的处理结果。此外出于简化动力学模型考虑也没有计入航速变化的影响，因此导致数值模型对于参数横摇幅值的计算精度有所降低。但结合其对于C11船模能否发生大幅参数横摇的预报效果，该模型总体上适用于实船参数横摇安全性评估。

图3 C11船模参数横摇响应对比Fig.3 Comparison of parametric roll response of C11

2 计算结果及风载荷影响分析

参考IMO采用Level 1衡准进行实船分析的结果[3]，本文选定了3艘集装箱船（C1～C3）和1艘散货船（B1）总计12个经批准的装载工况（系指实船被主管当局批准用于营运的装载工况）进行计算，分析风载荷对于实船参数横摇预报结果的影响。主尺度和装载工况见表1。

表1 实船主尺度Tab.1 Principal dimensions of full scale ships

续表1

本文对于实船的粘性阻尼均采用简化的Ikeda方法[21]进行计算。对于规则入射波条件下风力载荷影响的研究，计算航速为Fn=0.05、0.1和0.15，浪向为迎浪。入射波陡的选取与风载荷假定中关于恶劣气象条件的假定保持一致。以C3为例，入射波波高选取波长船长比为1.0时的总计3个波陡，波高分别为3.2 m、6.4 m和9.6 m。当采用Grim的等效波理论[24]，根据IACSRec.34北大西洋统计资料计算等效入射波波高，则有义波高4.5 m对应最大等效波高为3.2 m；有义波高6.5 m对应最大等效波高为4.6 m；有义波高8.5 m对应最大等效波高为6.16 m。因此，本文计算所采用的波陡系数涵盖了恶劣气象条件下的相应海况。

图4 风载对参数横摇响应的影响Fig.4 Effect of wind load on parametric roll

图4给出了风载对参数横摇运动收敛速度的影响以及对临界装载工况诱发参数横摇相应的对比。图5给出了是否计入风载时，船舶受到的横摇力矩和恢复力矩的对比结果。

在数值计算过程中，风倾力矩缩短了参数横摇响应发展的时间，促进横摇幅值更快趋于稳定。当装载工况遭遇的入射波陡接近诱发参数横摇的临界波陡时，该装载工况实际上处于临界状态，此时由于风载荷的作用从而诱发了稳定的参数横摇运动。由此可以认为风载荷对于诱发参数横摇起积极作用，降低了诱发参数横摇响应的入射波幅门槛。这表明，船舶即便遭遇相对较小的海况时，也可能在风倾力矩作用下诱发参数横摇响应。在实船预报中如果忽略风载荷的作用，有可能低估参数横摇的发生概率。

由图5可见，由风载荷引起的横摇力矩相对入射波力始终为小量。风倾力矩对波浪中GZ曲线的作用较为复杂，GZ曲线的最大值相对不计风载情况有显著提高，但峰值在不同周期也有显著降低，甚至引起GZ出现负值。

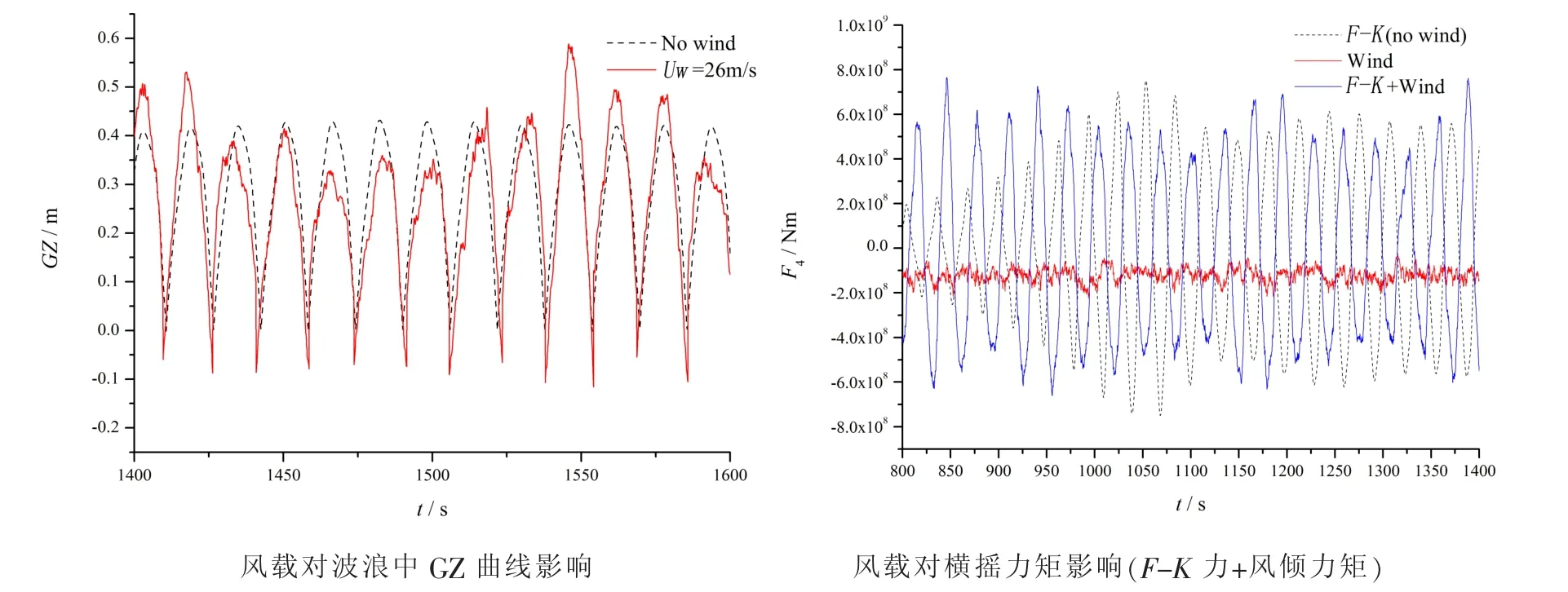
图5 风载对于横摇力矩的影响Fig.5 Effects of wind load on roll moment（C3-L4，Fn=0.05，λ/L=1.5，H/λ=0.01）

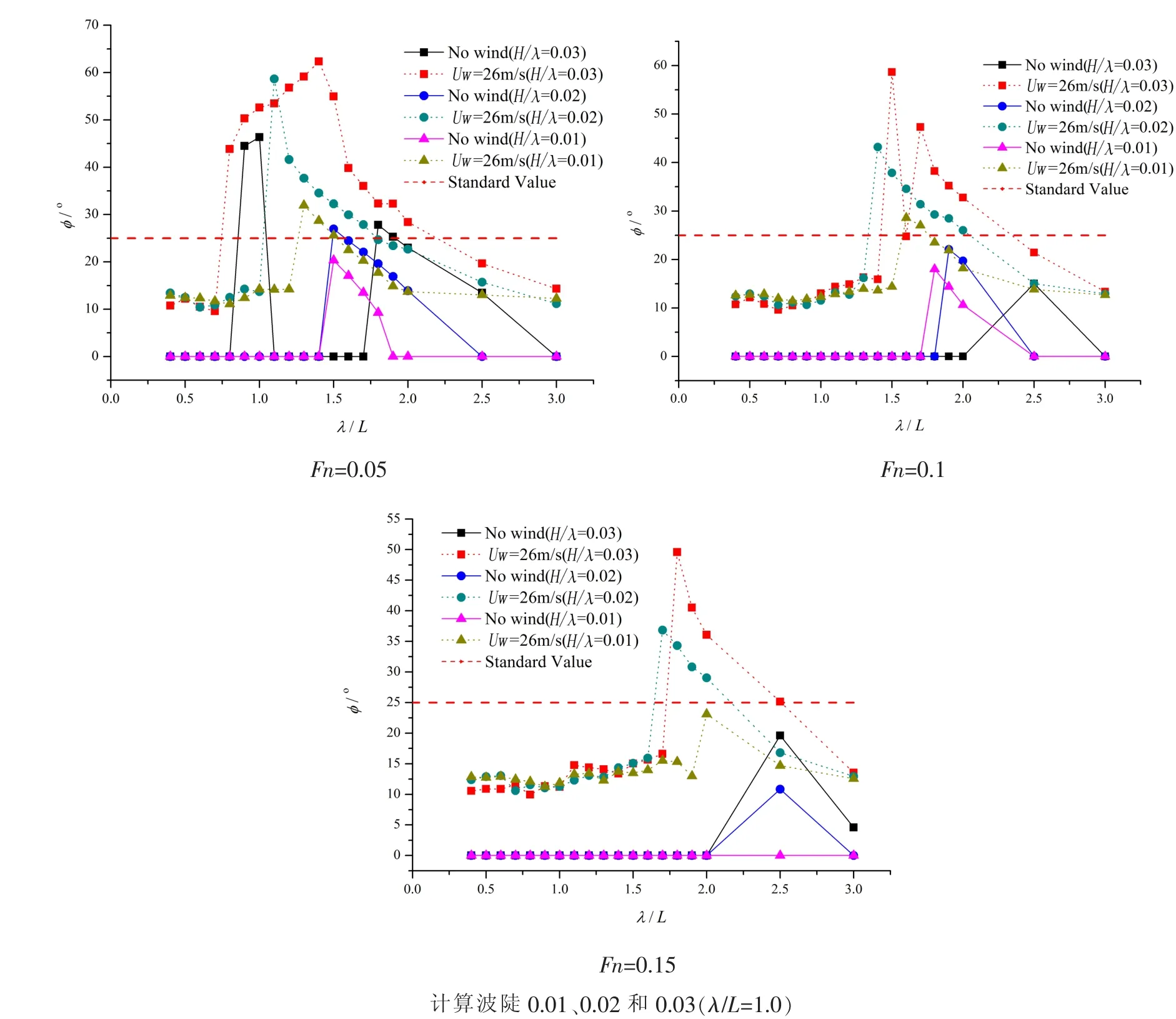
图6 风力载荷对横摇响应对应的入射波频率及其幅值影响（C3-L4）Fig.6 Effects of wind load on wave frequency and roll amplitude of PR(C3-L4)

图6给出了C3船的L4工况不同入射波波陡时，风载对参数横摇响应频率和幅值影响对比。计算结果表明，风倾力矩在无风情况的临界频率附近，诱发了参数横摇，即扩大了发生参数横摇的频率范围，并增大了参数横摇的幅值。这也证明风载荷对于诱发参数横摇起到促进作用。

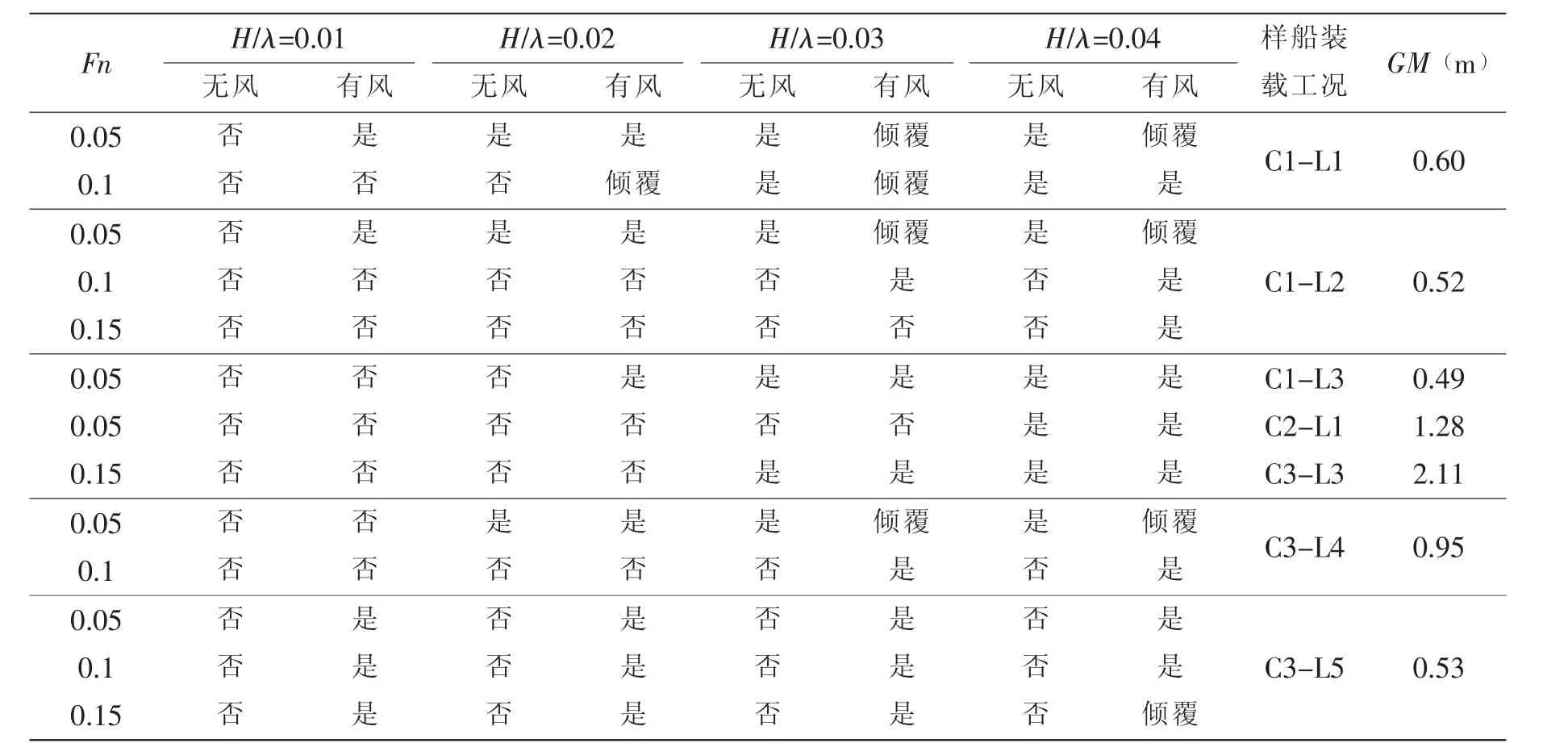
表2 对应不同GM的装载工况参数横摇预报结果（λ/L=1.0）Tab.2 Parametric roll prediction results of loading conditions with different GM values(λ/L=1.0)

表2给出了四艘实船的参数横摇预报结果，未发生参数横摇的装载工况不予列出。判断是否发生参数横摇的极限横摇角的标准值假定为25°。当横摇角达到60°时，假定船舶将由于进水点被淹没而倾覆。

结果表明，集装箱船C1～C3在风载荷作用下对于参数横摇的敏感性有所增强，风力载荷降低了诱发参数横摇所需的入射波陡，而散货船B1无论是否计入风载的影响均未发生参数横摇。这一结果与实船运营记录相符。与集装箱船的事故相反，散货船在恶劣海况下的实际运营中也从未报告发生过参数横摇事故。

造成这一现象的原因在于，一方面根据IMO的研究，ΔGM/GM值较大则对参数横摇更为敏感（ΔGM为波浪中GM的变化幅值），因此GM较大的装载工况将会具有更强的能力抵御由于波浪中GZ值变化诱发的参数横摇。散货船由于其船型特点，波浪中GM的变化幅值比较小，因此对于参数横摇现象相对不敏感，而集装箱船船型特点决定了其波浪中GM变化幅值相对较大，当集装箱船装载工况的GM值较小时，ΔGM/GM值相对较大。而且由于GM较小因此抵抗外界初始扰动的能力也相对较弱，此时风载荷能够引起相对较大的初始横倾（见表1），因此发生参数横摇的概率更高。对于GM值较大的装载工况（排水量和惯性矩相似时），由于其横摇固有频率较大因此也相对难以满足两倍遭遇频率的条件。

另一方面，由表1可见集装箱船由于甲板装载大量集装箱，承受的风力载荷远远大于散货船，因此风载荷对于集装箱船的影响更为显著。当入射波陡处于该装载工况发生参数横摇的临界波陡附近时，则该装载工况对GZ值的变化将十分敏感，此时足够强大的风力载荷对GZ曲线的扰动将足以诱发参数横摇甚至导致倾覆。

本文对于风载荷对实船参数横摇预报影响的研究所采用的海况条件是基于Grim的等效波理论换算的等效规则波。对于参数横摇响应的实船实海域短期预报，可采用ITTC双参谱进行不规则波条件下的模拟。但由于不规则波中参数横摇现象是非各态历经的[25]，数值模拟也会面临与模型试验相似的困难，即需要进行长时间的重复多次模拟。图7给出了对C3船的L4工况多次重复计算参数横摇响应的示意，每次计算模拟实船在迎浪长峰波中航行1小时。风载荷对于实船短期预报的影响有待进一步研究。

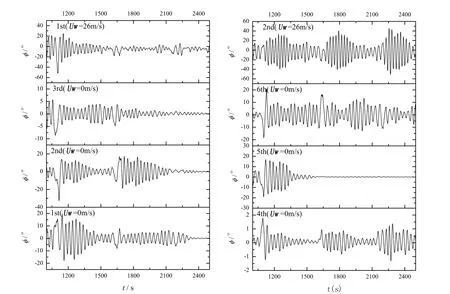
图7 C3装载工况L4长峰波计算示意（Fn=0.05，有义波高5.5 m，周期12.5 s）Fig.7 Simulation of parametric roll for irregular waves in head sea(Fn=0.05,Hs=5.5 m,TZ=12.5 s)

3 结 论

本文以四艘实船为研究对象，基于风浪耦合的三自由度弱非线性模型进行了规则入射波条件下参数横摇响应的仿真计算，研究了风力载荷假定对于实船参数横摇运动的影响。研究发现风载荷对于集装箱船参数横摇敏感性的影响较为显著，对于散货船基本没有影响。集装箱船GM较小的装载工况对于风力载荷的影响更加敏感。风力载荷的引入扩大了发生参数横摇的入射波频率范围，增大了参数横摇运动的幅值，同时降低了诱发参数横摇响应所需的入射波幅值，因此在实船预报中如果忽略风载荷的作用，有可能低估参数横摇的发生概率。

由于风载假定对于诱发参数横摇起到了促进作用，有助于帮助处于临界点的装载工况降低发生参数横摇的门槛从而引起事故，因此当航行中有可能无法规避恶劣气象、海况条件时对于此类装载工况需要采取适当的操作限制措施降低发生参数横摇的概率。

本文的研究表明了考虑气象条件对于实船参数横摇预报的重要性。因此未来开展实船实海域短期预报研究时，风载对于船舶参数横摇的影响应当引起足够的重视，探索有效的风浪联合作用下的数值模拟和水池试验验证方法尤其重要。

[1]France W N,et al.An investigation of head-sea parametric rolling and its influence on container lashing systems[C].SNAME Annual Meeting,2001 Presentation.2001:1-24.

[2]China.Proposal for Level 2 criteria of parametric rolling and excessive accelerations[C].Stability and Load Lines and on Fishing Vessels Safety(SLF)54th Session,2012:3-2.

[3]China.Sample verification and proposal of the draft level 1 criteria on parametric roll and pure loss of stability[C].Stability and Load Lines and on Fishing Vessels Safety(SLF)54th Session,2012:3-5.

[4]W G.Report of the working group at SLF 53(part 2)[C].Stability and Load Lines and on Fishing Vessels Safety(SLF)54th Session,2012:3-1.

[5]China.Comments on Level 2 criteria of parametric rolling(SDC 2/5/1)[C]//Ship Design and Construction 2nd Session,London:International Maritime Organization,2014:1-4.

[6]Japan.Information collected by the correspondence group on intact stability regarding the second generation intact stability criteria development(INF.8)[C]//Ship Design and Construction(SDC)1st Session,London:International Maritime Organization,2014:1-130.

[7]周耀华,张高峰,马 宁.基于IMO二代稳性衡准的实船参数横摇敏感性及衡准完善[J].上海交通大学学报,2016,50(3):425-436.Zhou Yaohua,Zhang Gaofeng,Ma Ning.Vulnerability check and further development of parametric roll criteria of 2nd generation of intact stability code of IMO based on full scale ship data[J].Journal of Shanghai Jiao Tong University,2016,50(3):425-436.

[8]Bulian G,Francescutto A.A simplified modular approach for the prediction of the roll motion due to the combined action of wind and waves[J].Journal of Engineering for the Maritime Environment,2004,218:189-212.

[9]Chang B C.On the parametric rolling of ships using a numerical simulation method[J].Ocean Engineering,2008,35:447-457.

[10]Germany.Further background information on the proposal by Germany with regard to the new generation intact stability criteria[C].Stability and Load Lines and on Fishing Vessels Safety(SLF)54th Session(2012),INF.7,2012.

[11]Naoya Umeda,Hirotada Hashimoto.An investigation of different methods for the prevention of parametric rolling[J].JMar Sci Technol,2008,13:16-23.

[12]Osman Turan,Zafer Ayaz.Parametric rolling behaviour of azimuthing propulsion-driven ships[J].Ocean Engineering,2008,35:1339-1356.

[13]Juncher Jensen J,Terndrup Pedersen P,Vidic-Perunovic Jelena.Estimation of parametric roll in a stochastic seaway[C].IUTAM Symposium on Fluid-Structure Interaction in Ocean Engineering,2008:141-154.

[14]Surendran S,Lee SK,Sohn K H.Simplified model for predicting the onset of parametric rolling[J].Ocean Engineering,2007,34:630-637.

[15]杨素军,范余明,等.大型集装箱船参数横摇模型试验研究[C]//2007年船舶力学学术会议暨《船舶力学》创刊十周年纪念学术会议.中国银川,2007:21-25.Yang Sujun,Fan Sheming,Nie Jun,et al.Model test study on parametric roll of large scale container ship[C]//2007 A-cademic Conference on Mechanics of Ships and the 10th Anniversary Commemorative Conference of ‘Ship Mechanics’.Yinchuan,China,2007:21-25.

[16]Fu L K,Jiang Z P.Numerical simulation of parametric rolling in longitudinal regular waves[J].Ship&Ocean Engineering,2007,04:34-37.

[17]常永全,范 菊,等.迎浪船舶的参数横摇分析[J].水动力学研究与进展,A辑,2008,23(2):204-211.Chang Yongquan,Fan Ju,et al.Analysis of ship parametric rolling in head sea[J].Chinese Journal of Hydrodynamics,23(2):204-211.(in Chinese)

[18]唐友刚,邝艳香,李红霞.初稳性高时变特性对横摇运动的影响[J].中国造船,2008,49(2):22-28.Tang Yougang,Kuang Yanxiang,Li Hongxia.Analysis of the influence of metacentric height fluctuations on roll motion[J].Shipbuilding of China,2008,49(2):22-28.(in Chinese)

[19]Lu Jiang,Umeda N,Ma Kun.Predicting parametric rolling in irregular head seas with added resistance taken into account[J].Journal of Marine Science and Technology,2011,16:462-471.

[20]陈京普,苏 甲,等.集装箱船参数横摇的非线性时域模拟[C].第二十三届全国水动力研讨会暨第十届全国水动力学术会议文集,2011:532-538.Chen Jingpu,Su Jia,Xu Jie,et al.A study on parametric rolling of container vessel in head waves by nonlinear time domain numerical simulations[C].Proceedings of 23rd National Conference on Hydrodynamics and 10th National Congress on Hydrodynamics,2011:532-538.

[21]Yuki Kawahara,Kazuya Maekawa,Yoshiho Ikeda.A simple prediction formula of roll damping of conventional cargo ships on the basis of Ikeda’s method and its limitation[C].Proceedings of the 10th International Conference on Stability of Ships and Ocean Vehicles,2009:387-398.

[22]Larsson Lars,et al.CFD in ship hydrodynamics-Results of the Gothenburg 2010 workshop[C].The Gothenburg 2010 Workshop,2010.

[23]W G.Report of the working group at SLF 55(part 1)[C].Stability and Load Lines and on Fishing Vessels Safety(SLF)55th session.Annex 1,2013:1-6.

[24]Grim O.Beitrag zu dem problem der sicherheit des schiffes in seegang[J].Schiff und Hafen,1961:490-497.

[25]Fossen T I,Nijmejer H.Parametric resonance in dynamical systems[M].2012:45-59.