冰区海上风电基础的抗冰性能分析

张大勇，王国军，王帅飞，佟保林，岳前进，罗成喜

（1.大连理工大学 海洋科学与技术学院，辽宁 盘锦 124221；2.大连理工大学 工程力学系，辽宁 大连 116023；3.中南勘测设计研究院有限公司，长沙 410001）

0 引 言

风能是一种可再生资源，且绿色环保，受到世界各国的大力发展。海上风能资源相对于陆地风能稳定，储量大，对周围环境影响小[1]。目前，越来越多的国家开始建立海上风电场，海上风电已经成为未来风电发展的趋势。

发电成本是制约风电发展的一个关键因素，欧洲研究表明，海上风电的风机基础投入占风机总成本的20%，同时，随着水深的增加风机基础的投入成本也会随之增加，有时甚至能达到总成本的30%[2]。因此，风电基础的合理设计就显得的更加重要。海上风电基础具有海洋工程结构、高耸结构、动力设备以及复杂地基环境的四种特性。目前，海上风电开发主要集中在浅海海域，风电基础以固定式桩基为主。基于海洋石油导管架平台基础设计，风电基础的形式主要为单立柱式单桩式和三桩基础式。由于风电基础的整体高度一般在60 m以上，远高于石油平台，因此风电基础相比导管架平台结构柔度更大。

近几年，我国海上风电场有了大规模的发展，包括渤海海域的多个风电场建设。在结冰海域设计和建造的风电基础及升压站结构必须具备一定的抗冰性能，确保电场冬季安全运行。海上风电基础大多属于典型的柔性直立结构，目前，寒区柔性抗冰结构的设计仍处于静力设计阶段,即只考虑最大静冰力或最大倾覆力矩，忽略了结构在动冰荷载下的性能，即动力失效模式。渤海辽东湾导管架平台的多年现场监测发现，海冰会引起柔性抗冰结构明显的动力放大，冰振响应十分显著，对结构及上部设备造成一定的影响[3-4]。

目前，直立结构极值冰力的计算方法多是基于早期的现场数据回归得到的经验公式。有学者对一些静冰力公式进行了比较分析[5-6]。尽管针对极值挤压静冰力的研究已经开展了数十年，一些研究成果也被设计规范所采纳，但冰力计算方法仍然没有得到统一的认识，不同方法计算的冰力差别很大[7]。直立桩腿结构的稳态振动是冰与结构相互作用的一种临界状态，Sodhi认为平台的稳态振动是一种强迫振动，而Blenkarn，Maattanen认为稳态振动属于自激振动。尽管强迫振动和自激振动观点的争论尚未达成统一，但近年来已经有越来越多的学者倾向于自激振动的观点。当冰速加快时，挤压破碎冰力随机性加强，频率锁定现象消失。Kärnä对大量实测冰力数据进行了谱分析，借鉴风速谱分析结果，得到了海冰脆性挤压破碎冰力谱[8]，尽管该模型已应用到我国渤海新型柔性抗冰平台的设计中，但其中的参数还有待进一步完善。

海上风电基础现有的设计规范是以风、波浪、地震等为主要的海洋环境控制荷载，其中相关的动力响应研究比较完善[9]。抗冰设计存在许多关键性问题尚未得到解决，如冰与该类结构的相互作用、冰振引起结构的失效模式等。渤海导管架平台的桩腿直径一般在1-2 m，而风电基础水面处的直径一般在4-5 m。为了合理建设渤海海上风电场，对目前海上风电基础的抗冰性能分析是十分必要的。本文首先基于多年现场冰与结构作用观测及冰荷载的研究成果，明确了海冰与风电基础结构的作用形式。其次提出了柔性抗冰结构设计中应考虑的主要失效模式及评价方法。最后，以渤海某典型风电基础为例，对其抗冰性能进行评价，进一步明确风电基础结构在抗冰设计及安全保障中需要考虑的关键失效模式。本文的研究可为寒区风电场的开发提供合理依据。

1 海冰与风电基础结构的相互作用

1.1 宽窄结构判定

海冰与直立结构相互作用时，会出现多种破坏形式，主要有劈裂、弯曲、屈曲和挤压等，其中挤压破坏对结构的影响最大。由于不同结构尺寸前海冰的破坏和冰力存在显著差异，为了明确冰荷载模型的适用范围，可以通过定义宽窄结构的方法。传统方法从结构尺寸定义宽窄结构，但相同的结构尺寸，不同的海冰破坏行为也会导致冰力不同，需要进一步明确宽窄结构的判定。

海冰与圆柱腿结构相互作用时，在不同的加载速率下表现出不同的力学行为，较低应变速率下是以塑性变形为主的韧性破坏，较高应变速率下表现为断裂为主的脆性破坏，而在从韧性到脆性的过渡阶段存在一个转变区。目前，我国渤海地区直立结构上的静冰力模型是基于API-RP-2N规范[10]，并通过渤海多个平台的多年监测数据进行修正得到的。从渤海平台的监测数据看出，海冰与结构相互作用时海冰存在同时破坏现象[11]，即各局部冰力具有明显的周期性，且加载和卸载过程保持同步，产生的总冰力也呈现明显的周期性变化，并且冰力极值较高（如图1所示）。渤海导管架平台的实测冰力数据表明，当平整冰以较慢的冰速挤压作用在圆柱腿结构上时，同时破坏现象会更为显著。图2是实测的挤压静冰力作用时局部冰力随时间变化的同步曲线，可以看到代表局部冰力的3条曲线同时加载、同时卸载，表现出很明显的同时破坏特征。可见，低冰速下冰板与直立结构之间的“全接触”是发生同时破坏的必要条件。

图2 局部冰力的同步导致总冰力上升Fig.2 Synchronization of local ice forces lead to total ice force increase

海冰在结构前发生脆性破坏，破碎冰能够及时清除，后续冰板能够再次作用在结构上，发生新的破碎过程，则结构前海冰可能发生同时破碎。海冰的破碎过程主要是由破碎冰的尺寸、数量和结构水线尺寸决定的。从实际观测发现，对于较窄的结构破碎冰能在短时完全清除，对于较大尺寸的结构，破碎冰清除受阻，常会在结构前发生冰堆积现象。当发生冰堆积时，会直接影响冰与结构的作用过程，结构前的冰破碎模式将发生变化，同时冰板作用在堆积冰上，荷载通过堆积冰传向结构，由于堆积冰比较松散，整体强度将显著降低，传递过程中能量显著耗散，将不存在作用在直立结构上的同时破坏现象，冰荷载模型也将发生改变，图3为海工结构前的冰堆积形成过程示意图。

图3 海工结构前冰堆积形成过程示意图Fig.3 Developing process of front ice jams

基于现场实测数据发现，交变冰力在时间周期内经历加载（海冰破碎）过程、卸载（破碎冰清除）过程。当完整冰板与结构直接作用发生周期性破坏时才可能产生动冰力，破碎冰不会在结构前发生堆积，不影响海冰与结构的直接作用，此时海冰破碎与破碎冰清除的相似性形成周期过程，即结构的加载、卸载周期过程，从而形成交变冰力。若破碎海冰在结构前能够在短时间内清除,不影响海冰在结构前的破坏模式和破坏过程，则会发生海冰的持续破坏和交变冰力，引发显著的结构冰激振动，如图4所示；若破碎海冰不能在结构前清除，是形成持久的堆积，后续完整的运动冰板不能够直接作用在结构上，取而代之的是冰作用在堆积冰上，通过堆积冰向结构传递荷载。此时，结构的冰振响应并不显著（如图5），则不会发生海冰破坏所引起的交变冰力。

图4 未发生冰堆积时结构的冰激振动Fig.4 Significant ice induced vibration without ice accumulation

图5 冰堆积时结构的冰激振动Fig.5 Ice induced vibration with ice accumulation

基于以上分析，提出直立腿宽窄结构的判定：

（1）窄结构是指破碎冰能够及时从结构两侧清除，不产生堆积，后续冰能够直接作用在结构上。低冰速下存在海冰挤压同时破碎的可能性，快冰速下将产生显著的交变冰力。

（2）宽结构指破碎冰不能够及时地从结构两侧清除，在结构前发生冰堆积现象，形成永久堆积冰。低冰速下海冰发生挤压非同时破坏，可以采用低值冰力公式；快冰速下不易产生明显的冰激振动。

根据现场监测以及宽窄结构的判定方法，发现对于某些尺寸足够宽大的结构，冰堆积现象常常发生，对于结构尺寸居中的，存在冰堆积现象和冰清除现象。尺寸较小的结构，薄冰情况下会产生较小的破碎尺寸，破碎冰在清除前会保留一段时间，形成“堆积”。尺度较大的结构，在厚冰下，断裂冰板很大，破碎冰也能够在短时间内清除，而不会对后续冰与结构的作用产生任何影响，如Confederation大桥桥墩发生的显著冰激振动。

可见，对于海冰与风电基础相互作用，在厚冰（10 cm以上）下表现出窄结构的海冰挤压破坏行为，慢冰速时海冰会发生挤压同时破坏，快冰速下海冰的破碎会及时清除，结构会产生显著的冰激振动现象。

1.2 风电基础结构的动力特性分析

本文结合数值模拟和海冰与窄体结构相互作用的现场监测，选取渤海某拟建的风电基础和导管架式平台（具体参数如表1所示），两者均是单立柱三桩形式。通过对比分析，明确风电基础的结构动力特性。风电基础以及塔筒部分采用shell181单元，建模中对顶部风电机组采用Mass21质量单元模拟，桩基部分采用6倍桩径方法简化处理，如图6所示。基于数值模拟，风电基础的前四阶固有频率及振型图如表2所示。

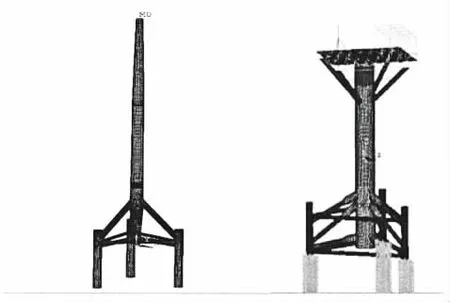
图6 风电基础与导管架结构简化有限元模型Fig.6 Simplified finite element model of wind turbine foundation and jacket structure

表1 独腿导管架平台结构参数Tab.1 Single-legged jacket platform structure parameters

表2 风电基础的前4阶频率及振型Tab.2 Four natural frequencies and mode shapes of wind turbine foundation

分析发现，风电基础结构的基频为0.34 Hz，独腿导管架平台的基频为0.94 Hz，结构的前三阶均是X方向振动、Y方向振动、Z方向扭转。风电基础结构的柔度相比导管架平台更大。Kamesaki等[12]指出挤压冰力随着结构刚度的下降而增加，这说明柔性结构上更容易发生海冰挤压同时破碎。准静态过程中，柔性结构的最大位移较大，在冰力突然卸载后结构回摆过程中结构与冰板的相对速度也较大，使得破碎冰块可以被挤出。在稳态振动过程中，柔性结构的振幅及回摆速度很大，使得破碎冰块得以清除，结构与冰板的“全接触”得以发生。另外，基于现场海冰监测发现，冰与柔性抗冰结构发生破碎的能量谱频率多数集中在0-1 Hz之间，如图7所示。这样，柔性结构固有周期与冰力周期十分接近，不可避免地存在冰激共振现象，结构动力效应明显。

1.3 风电基础的冰荷载模型

由于风电基础结构直径大于典型的导管架结构（窄结构），但明显小于重力式结构（宽结构）。以上分析发现，冰厚较大时，破碎冰块可以及时被清除，结构与冰板会发生“全接触”情况，风电基础结构表现为柔性窄结构的冰振特性：

（1）冰速很慢时，海冰会发生准静态（间歇）挤压破碎，结构发生准静态振动；

（2）冰速缓慢增加，冰的破碎过程会与结构振动产生耦合，此时产生频率锁定的自激冰力，结构发生简谐形式的稳态自激振动；

（3）冰速较快时，冰板会发生脆性挤压破碎，结构响应变为随机激励下的受迫随机振动。

1.3.1 极值静冰力模型

采用API RP-2N规范要求，极值静冰力公式可以表示为：

其中：α是折减系数，选取0.3-0.7（规范要求，属于非同时破坏的低值冰力），基于现场监测发现，对于同时破坏，该系数应明显高于规范要求，建议取1.0；σc是海冰单轴压缩强度，h是冰厚。

图7 冰与直立结构作用的冰力能量谱Fig.7 The power spectrum of ice load

1.3.2 稳态冰力模型

当冰速不是很快时（一般为几厘米到十几厘米每秒），结构有可能在冰的作用下发生强烈的稳态振动。通过对冰激稳态振动发生时，结构交变位移和交变冰力的同步时程曲线分析发现冰力是一个周期性过程，它的变化频率被“锁定”在结构的振动频率上。

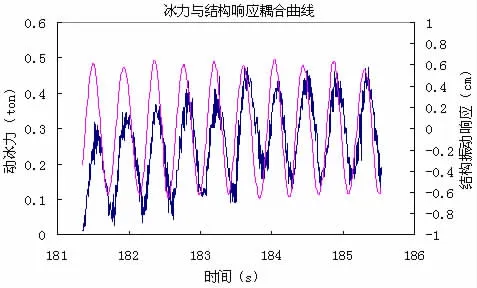
图8 冰激稳态振动时冰力和结构振动位移的耦合时程曲线Fig.8 The ice force and structural vibration displacement under ice induced steady state vibration

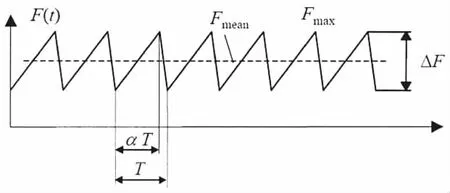
图9 稳态冰力模型Fig.9 The model of steady state ice force

对冰激稳态振动的实测响应进行频谱分析也证明了这一结论，振动能量集中在结构的一阶固有频率上。为了初步计算冰致自激振动的幅值大小和周期，Kärnä[13]根据渤海实测的自激振动冰力时程，给出了三角波时域函数，表征产生自激振动的冰力随时间的变化特征，如图9所示，图中：Fmax是冰力最大值，可保守取为极值静冰力；ΔF=qFmax，q=0.1～0.5；Fmean为冰力平均值，可通过Fmax-ΔF/2计算；T为冰力周期，计算中可近似取为结构固有周期；α是加载阶段系数，通常选取0.6-0.9。

1.3.3 随机冰力模型

当冰速很快时，冰板在结构上发生连续不规则的脆性挤压破碎，由于接触面上冰的碎块大小不一，且压力分布不均，由此形成的合力为不规则的随机变化，同时引起结构的随机振动。图10是基于实测的随机挤压冰力和结构振动的时程曲线。

Kärnä和Qu[8]根据渤海和波斯尼亚湾灯塔上测得的大量样本的随机冰荷载数据，经过统计分析建立了随机冰力谱：

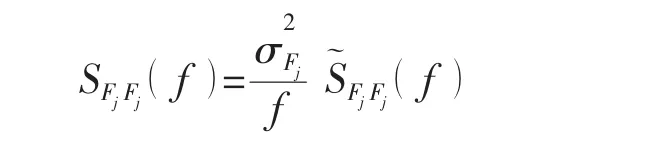
图10 随机动冰力和结构随机振动时程Fig.10 The random ice force and structural vibration

2 海冰作用下柔性结构的失效模式

结构的柔性应该从两方面考虑：一是在极值静荷载下，结构产生了不可忽略的变形；二是在动荷载作用下，结构动力效应明显。可见，风电基础与导管架平台等类似结构在海冰作用下属于第二种类型。本文对冰荷载作用下柔性抗冰结构的失效模式及评价方法做以下分析。

2.1 极端荷载下结构的失效

目前的海工结构规范设计中，一般考虑地震、波浪、海流、风和海冰作用，并转化为等效静力作用来考虑。主要通过强度要求、刚度要求，来评估结构或者构件在各种载荷组合作用下是否安全。强度要求就是指构件在设计载荷作用下的设计应力应当小于许用应力，即σ＜[σ]；刚度要求是指结构的最大变形应当小于规范建议的容许值，即λ＜[λ]。对于抗冰结构，就是在极端静冰力的作用下保证结构的强度、刚度要求。在API RP-2A或ISO/DIS 19902标准中，极限强度分析采用储备强度比作为评价指标[14-15]。海洋结构体系的储备强度系数可按下式计算:

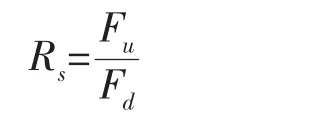
其中：Fd和Fu分别是平台结构在设计荷载下和极限荷载下的基底横向力或倾覆力。文献[16]指出，当结构安装水深大于30 m时，宜用结构的倾覆力矩定义结构的储备强度系数；而当安装水深小于30 m时，用结构基底横向力定义强度储备系数更为合适。

2.2 动冰荷载下结构的疲劳失效

多年的现场观测发现，渤海辽东湾的柔性抗冰结构在动冰荷载的作用下存在明显的动力放大效应，从定性上看有必要进行动力分析。为了更好地说明柔性抗冰结构存在冰激疲劳失效，还必须证明在常规冰情下冰荷载引起的结构热点应力超过了材料的疲劳极限应力，即从定量上进一步说明这个问题。

风电基础结构的冰激疲劳损伤是由于热点应力反复作用引起的，利用有限元数值模拟，对结构的热点疲劳应力进行分析，合理地考虑结构应力集中系数。另外，根据API规范提供的S-N曲线，当无限寿命取N=108次时，疲劳极限应力为41 MPa。在常规冰情下，若冰激振动造成的热点动应力大于疲劳极限应力则说明冰振可能存在结构的疲劳失效，需要进行详细的冰振疲劳分析，即冰振下结构的疲劳寿命估计。与波浪环境下海洋结构相比，冰区结构疲劳寿命分析的主要区别在于疲劳冰荷载与冰疲劳环境参数，这也是风电基础结构冰激疲劳分析的两个瓶颈问题。冰振结构疲劳失效评估流程如图11所示。

图11 冰振柔性抗冰结构疲劳失效评估流程Fig.11 The fatigue failure assessment process of the flexible ice-resist structures

2.3 冰振响应引起的失效

监测发现，海冰与平台作用时，可以激起平台较大的加速度响应。特别是对生产天然气的平台，上部布置错综复杂的天然气管线，这些管线在长期的冰振作用下，可能导致平台上部天然气管线断裂与法兰松动的事故隐患。同样，冰激风电基础结构会引起上部电机及附属设备的振动。依据电机的振动标准，振动位移、速度的均方根值是评价指标。

风电基础结构在冰激作用下的振动方向主要以水平为主，并且振动响应主要集中在结构的基频。由于结构振动响应是随机的，对于离散的监测数据，等效振动响应的均方根采用下式计算：

其中：ai表示 ti时间内测得的结构位移、速度、加速度等均方根值，mm，mm/s，mm/s2；ti是序号为 i对应的时间，s。

一般来讲，影响冰力大小的主要因素有冰厚、冰速和冰破碎强度。在相同的海域，冰破碎强度变化不大，因此这里只选择冰速和冰厚来描述冰况。由于冰速和冰厚的分布是不相关的随机过程，即某一特定冰厚下，各种冰速都可能出现，因此可以按照冰速和冰厚的组合来描述冰况。对于每一种冰况，计算相应的冰荷载谱，将冰荷载谱输入到结构模型中，在频域内进行动力分析，就可以求得结构在这种冰况下的振动响应统计值。重复上述步骤，就可以得到所有冰况下平台的振动统计值。

2.4 冰激振动对基础的影响

在不排水的条件下，饱和无粘性土或稍具有粘性的土，由于振动载荷（主要是地震）的连续作用，产生超静孔隙水压力，并逐步发展。当超静孔隙水压力（简称孔压）等于上覆土压力时，土颗粒将悬浮于土孔隙水中，呈现出类似于稀砂浆或稀泥浆的状态。土的这种因孔压上升，粒间有效应力下降，导致固态转变为液态从而失去强度，丧失稳定的现象，称为“液化”。液化是一种特殊的动强度问题，大多发生在疏松的饱和粉砂、细砂中，发生条件是大应变幅。在海冰与平台相互作用时桩腿会发生冰激振动现象，对桩腿相连接的基础将产生一定的影响。上世纪八十年代波福海的Molikpaq沉箱的地基在冰振作用下产生了液化[17]。对于浅基础（一般在8-10 m以下），强烈的冰激振动可能对基础产生一定的危害。冰激振动引起基础的振动响应属于周期性的动载荷，基础的振动对其周围的土体产生动应变效应。

2.5 冰荷载作用下风电基础结构的失效模式及判别指标

基于以上分析，柔性抗冰结构的主要失效模式归结为以下几种：

（1）结构安全失效模式。包括极值静冰力作用下结构最大变形或强度超过极限值而引起结构破坏；动冰荷载作用下结构的疲劳破坏及桩基破坏。

（2）上部设备失效模式。结构在动冰力作用下，电机及附属设备的强烈持续振动而影响其正常使用性能。

上述各种失效模式及判别指标汇总于表3。

表3 海冰作用下风电基础各种失效模式的判别指标Tab.3 Discrimination index of ice-resistant platform failure modes

3 实例—渤海某风电基础抗冰性能评价

基于本文提出的柔性抗冰结构失效模式及相应评价方法，对渤海某风电基础结构进行冰荷载下的抗冰性能评价，进而明确该结构在抗冰的概念设计中应关注的主要失效模式。该风电基础为单立柱三桩式结构，风机顶部质量140 t，塔筒高度80 m，设计水深20 m左右，设计风速为25 m/s（50年一遇），设计波高为3.99 m，周期为6.7s（50年一遇），设计冰厚为38 cm（50年一遇）。风机桩腿直径是2.5 m，桩腿长度为73 m。

3.1 极值静冰力下结构失效分析

为了合理的考虑到极值荷载对基础结构的影响，本文利用combin39弹簧单元采用p-y曲线模拟桩土相互作用，风机基础的有限元模型如图12所示。

图12 三桩风电基础桩土P-Y曲线有限元模型Fig.12 The finite element model of three wind turbine foundations with P-Y

图13 风电基础冰为主要荷载下结构应力云图Fig.13 Structure stress nephogram considering sea ice loading

图14 风电基础冰为主要荷载下结构位移云图Fig.14 Structure displacement nephogram considering sea ice loading

图15 无冰情况下风电基础结构应力云图Fig.15 Structure stress nephogram with no ice action

图16 无冰情况风电基础结构位移云图Fig.16 Structure displacement nephogram with no ice action

表4 极端工况下风机基础的最大应力与变形Tab.4 The maximum stress and deformation under the extreme condition

选取极端（50年一遇）环境荷载，其中海冰压缩强度为1.99 MPa。考虑结构的重要系数为1.1，分析以海冰为主要荷载时风机基础的结构响应，取风荷载安全系数为1.05，冰荷载安全系数为1.5。

图13-16分别为有冰和无冰极端条件下风电基础结构的应力与变形云图，对比发现：极端冰荷载下结构响应远大于未考虑冰荷载的情况，并且考虑极端静冰荷载时结构的最大应力更接近安全值。因此，极值静冰荷载是风电基础抗冰性能分析中必须考虑的问题之一。

3.2 动冰力下风电基础的疲劳失效

对于动冰荷载下风电基础的疲劳失效，本文首先分析结构在常规冰况下热点应力，包括冰厚为24 cm时结构发生稳态振动；冰厚为18 cm，冰速为30 cm/s时，结构发生随机振动。通过计算分析，结构的热点位于斜撑与桩腿连接处，如图17所示。稳态振动下，结构的疲劳应力循环值在38 MPa左右，随机振动情况下结构的疲劳应力标准差在16 MPa左右，根据API规范提供的S-N曲线，当无限寿命取N=108次时，疲劳极限应力为41 MPa。

图17 冰激振动下风机基础的热点位置Fig.17 The hot spot location under ice induced vibration

结果表明，稳态振动下可能会使结构发生疲劳破坏；而随机振动下，结构的热点应力很小，不会造成热点疲劳失效。由于稳态振动的发生频率较低，且持续时间很短，冰激风电基础结构的稳态振动是否会引起结构的疲劳失效，还需要进行详细的疲劳寿命估计。

3.3 动冰力下风电基础的振动失效

本文选取冰厚为38 cm时结构发生稳态振动的极端冰况，采用简化的三角波稳态冰力函数，将其施加在风电基础水面处，利用瞬态分析方法，得到整体结构的冰振加速度、位移等时程曲线，如图18，19所示。结果表明，风机顶部振动加速达到90 cm/s2，位移达到25 cm，如此强烈的冰激振动可能影响风电基础上部电机及附属设备的正常运行，需要针对具体电机及设备，结合国家标准详细校核。

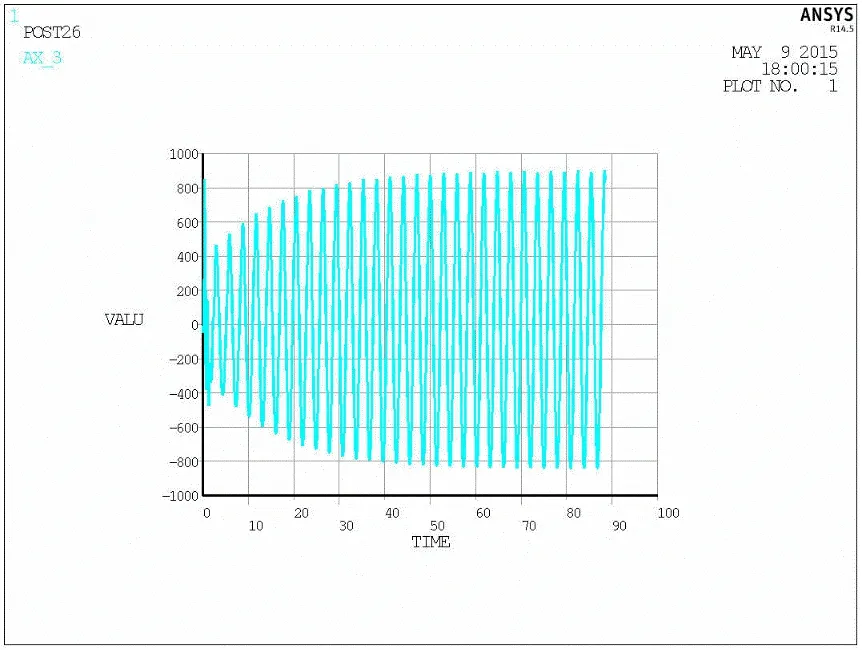
图18 稳态振动下风机轮毂处的加速度响应曲线Fig.18 The acceleration response curve of hub under ice-induced vibration

图19 稳态振动下风机轮毂处的位移响应曲线Fig.19 The displacement response curve of hub under ice-induced vibration

3.4 冰激振动对基础的影响

本文采用combin39单元模拟土壤，泥面以下的桩腿每隔0.5 m建立X、Y、Z三个方向的弹簧，利用p-y曲线法模拟桩—土作用，模型中各层的土壤参数如表5所示。选取的冰况是：冰厚=38 cm时，结构发生强烈的稳态振动。由于冰振主要引起结构水平方向的振动，基于ANSYS瞬态分析，得到不同深度下土体的变形，如表6所示。结果表明，泥面以下7 m内土壤的变形幅值为1.4 mm左右（图20所示），在10 m到20 m土壤的变形幅值为0.1 mm左右（图21所示），而在40 m以下土壤变形交变值为10-3mm以下，几乎不会引起土壤变化。由于风电基础结构属于深桩基础，桩基深度为60 m，冰激振动不会引起土壤的承载力不足而造成结构整体失效。

图20 泥面以下7 m处土壤的动位移曲线Fig.20 The displacement curve of soil(depth=7 m)

图21 泥面以下10 m处土壤的动位移曲线Fig.21 The displacement curve of soil(depth=10 m)

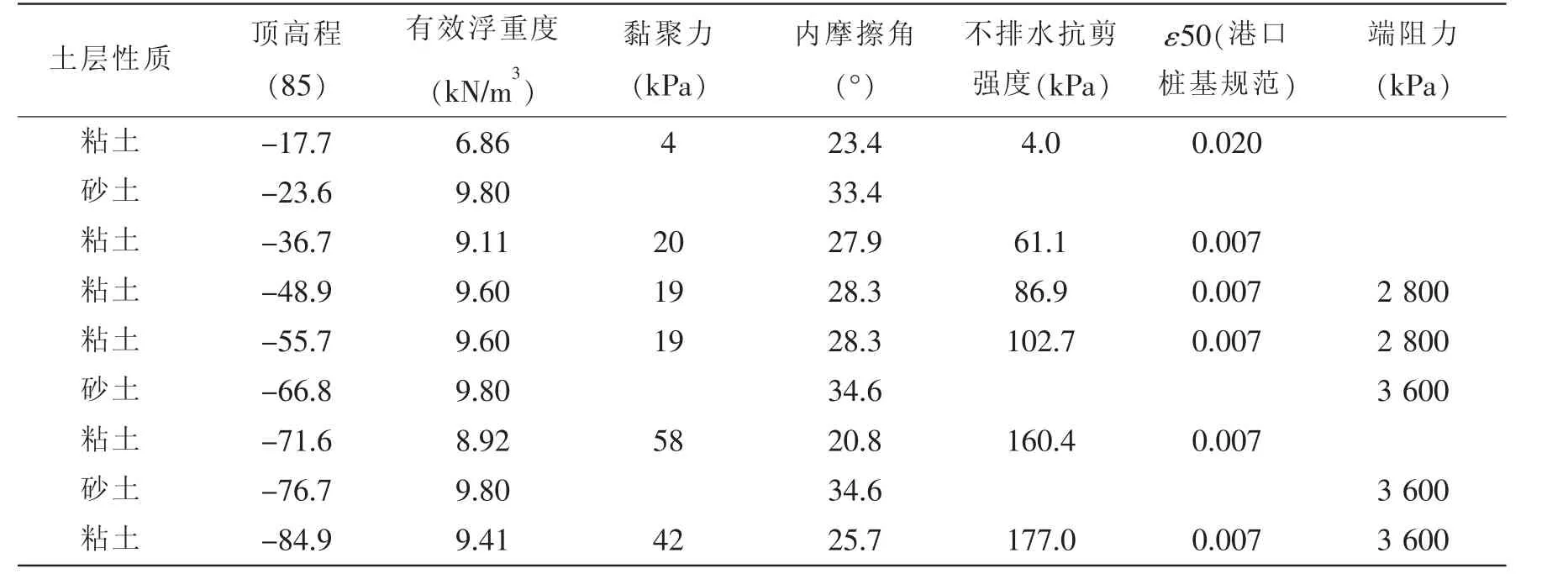
表5 土壤材料参数Tab.5 Soil parameters

4 结 语

风电基础属于典型的柔性结构。由于风电场在冰区还没有大规模建设，该类结构目前的设计是否满足抗冰性能要求，动冰荷载是否对结构造成影响还没有得到充分的认识。

本文基于多年的渤海海冰现场监测，首先明确海冰与风电基础结构相互作用形式，提出在厚冰下表现出窄结构的海冰挤压破坏行为：慢冰速时海冰会发生挤压同时破

坏，快冰速下海冰的破碎会及时清除，结构会产生显著的冰激振动现象。其次，选取渤海某拟建的风电基础，利用数值模拟，明确其结构力学特性，分析发现，结构的整体刚度及固有频率远低于渤海典型的导管架平台，存在明显的动力放大现象。基于现场冰与抗冰平台相互作用的观测以及冰荷载的研究成果，明确了风电基础结构的冰荷载模型，并提出冰荷载作用下柔性抗冰结构的失效模式及判别指标及评价方法。最后，以渤海某拟建风电基础为例，对其抗冰性能进行评价。结果表明，目前风电基础设计虽然能满足极值静冰荷载要求，但是极值静冰荷载时结构的最大应力及变形要远大于未考虑冰荷载时；风电基础的冰振响应显著，对电机及配套设备会造成较大影响；稳态振动下基础的热点应力较大，该冰况下可能会引发疲劳失效；冰激振动下基础周围土体变形较小，不会发生土壤失效。本文的研究可为寒区风电基础的抗冰设计及安全保障提供合理依据。

表6 土层不同深度处的土壤位移幅值Tab.6 The displacement amplitude at different depths of soil layer

[1]周艳荣,张 巍,宋 强.国内外海上风电发展现状及海域使用中的有关问题分析[J].海洋开发与管理,2011,28(7):6-10.Zhou Yanhong,Zhang Wei,Song Qiang.Current situation of offshore wind power development in China and related problems in the use of sea area[J].Ocean Development and Management,2011,28(7):6-10.

[2]Snyder B,Kaiser M J.Ecological and economic cost-benefit analysis of offshore wind energy.Renew Energy[J].Renewable Energy,2009,34(6):1567-1578.

[3]张大勇,车啸飞,岳前进等.渤海单立柱桶型基础平台抗冰振分析[J].船舶力学,2011,15(8):915-920.Zhang Dayong,Che Xiaofei,Yue Qianjin.Structural ice-resistant performance analysis of offshore bucket foundation platforms with a single pillar[J].Journal of Ship Mechanics,2011,15(8):915-920.

[4]Zhang Dayong,Xu Ning,Yue Qianjin,Liu Di.Sea ice problems in Bohai Bay oil and gas exploitation[J].Journal of Coastal Research,2015,73:676-680.

[5]Bjerkas M.Global design ice loads dependence of failure mode[C]//Proceedings of the 14th International Offshore and Polar Engineering Conference.Toulon,France,2004:871-877.

[6]史庆增,宋 安.海冰静力作用的特点及几种典型结构的冰力模型试验[J].海洋学报,1994,16(6):133-141.Shi Qingzeng,Song An.Static characteristics of sea ice and ice force model test of several typical structures[J].Acta O-ceanologica Sinica,1994,16(6):133-141.

[7]Timco,Croasdale.How well can we predict ice loads[C].Proceedings of the 18th IAHR International Symposium on Ice,2006:167-174.

[8]KärnäT,Qu Y,et al.A spectral method for forces due to ice crushing[J].Journal of Offshore Mechanics and Arctic Engineering,2007,129:138-145.

[9]陈 前,付世晓,邹早建.海上风力发电机组支撑结构动力响应特性研究[J].船舶力学,2012,16(4):408-415.Chen Qian,Fu Shixiao,Zou Zaojian.Investigation on dynamic response characteristics of offshore wind turbine support structure[J].Journal of Ship Mechanics,2012,16(4):408-415.

[10]API RP-2N.Recommended practice for planning,designing,and constructing fixed offshore structures in ice environments[S].1988.

[11]张 希.冰激直立结构稳态振动[D].大连:大连理工大学,2002.Zhang Xi.Steady state vibration of vertical structure induced by ice vibration[D].Dalian:Dalian University of Technology,2002.

[12]Kamesaki K,Yamauchi Y,KärnäT.Ice force as a function of structural compliance[C]//Proc.13th Int.Symp.on Ice.Beijing,1996,1:395-402.

[13]KärnäT,et al.An upper bound model for self-excited vibrations[C].Proceedings of 19th International Conference on Port and Ocean Engineering under Arctic Conditions(POAC),2007:177-189.

[14]API RP-2A WSD.Recommended practice for planning,design and constructing fixed offshore platforms-Working stress design[S].API Recommended Practice 2A-WSD,21 Edition,2000.

[15]ISO/DIS 19902.Design of fixed steel jackets[S].DISDraft.International Standardization Organization,2004.

[16]申仲翰.钢结构海上平台整体安全性评估方法研究[J].中国海洋平台,1994,Z1:140-146.Shen zhonghan.Research on global safety assessment method of steel structure offshore platform[J].China Offshore Platform,1994,Z1:140-146.

[17]Wright B,Timco GA.Review of ice forces and failure modes on the Molikpaq[C]//Proc.12thInt.Symp.On Ice.Trondheim,Norway,1994,2:816-824.