循环载荷下箱型梁极限强度性能实验研究

崔虎威 ， 杨 平 ， 周 杨 ， 高 尚

（1a.高性能船舶技术教育部重点实验室（武汉理工大学），武汉 430063；1b.武汉理工大学 交通学院，武汉 430063；2.武汉交通职业学院，武汉 430065）

0 引 言

船舶结构的安全性直接关系到船舶自身、及其所载货物及人员的生命财产安全，而船舶的总纵强度又是船舶结构安全性最重要的保证。为了确保船舶具有足够的总纵强度，需要准确地评估船舶的总纵弯曲极限承载能力（极限强度）。目前在船舶极限强度研究领域，已经在理论分析、数值仿真、模型实验等方面都取得了长足的进步。但需要指出的是：目前的研究绝大多数都基于船体在一次性极值弯矩作用下，发生总纵失效而崩溃，且研究的关注范围都集中于从局部构件屈曲、屈服到大范围的构件失效直至极限状态，没有关注船体梁后极限强度剩余承载能力特性[1-4]。事实上，船体结构的总体折断破坏更为符合实际且普遍的情况是在恶劣海况中多次极值外载作用下的累积递增塑性破坏，即多次发生超过弹性范围的循环载荷下中拱及中垂后的结果[5]。与一次性崩溃的评估方法相比，考虑船舶在实际海况下承受多次较大外弯矩导致的船体塑性累积变形，并研究其对极限强度的影响应更加合理。目前现行的总纵强度一次性崩溃评估体系可能会过高估计船舶的实际总纵强度，使得其对实际船舶总纵强度的评估偏于危险。另外，从基于船体梁风险设计理念来看，船损事故的灾难程度归结于其造成了多大的损失，而损失的大小又与船体结构崩溃的严重性密切相关，因此船舶的后极限强度承载性能对灾难的严重程度就十分重要，研究循环载荷下船体梁总纵后极限强度特性，目前已经开始得到一些学者的重视[6-7]。

模型实验是研究船体结构极限强度的重要方法之一。采用模型实验可以直观地观察结构在外载作用下，从局部到整体，逐步渐进的崩溃过程。由于箱型梁的结构型式及力学特性类似船体结构，对其开展实验研究，可为船体结构极限强度理论预报方法的验证提供具有参考价值的数据和结论。Reckling[8]针对七个箱型梁模型进行了系列纯弯崩溃测试；Ostapenko[9]对三个箱型梁模型进行了弯曲、剪切和扭转联合作用下的崩溃测试；Nishihara[10]对分别代表单壳油船、双壳油船、散货船和集装箱船等四类船型的八个箱型梁模型进行了测试；Mansour[11]进行了两个模型的相似性实验。

目前已有文献来看，开展循环弯曲下的船舶结构模型极限承载性能的实验不多。Fukumoto[12]做了薄壁箱型梁模型实验，以研究其在循环弯矩载荷下的极限强度，实验模型没有考虑加强筋的影响。黄震球[5]开展了箱型梁在循环弯矩作用下的极限强度的实验研究，但其实验载荷没有形成真正的中拱-中垂循环，只是单向的多次加载。Xu[6]等对波浪载荷下的船体箱型梁开展了实验研究。

循环载荷下的箱型梁的极限承载性能，包含了后极限强度承载能力特性。此类研究既包含常规的极限强度研究，又有非线性破坏后箱型梁力学行为的延伸，同时具有材料和几何的强非线性、破坏模式多样化和后屈曲路径难以把握等特点。本文从实验角度，对循环弯曲下的箱型梁极限承载性能进行了研究。

1 循环载荷下箱型梁极限承载性能实验方案

1.1 箱型梁系列模型的设计与制备

为了考虑不同材质、加强筋疏密以及循环载荷模式对箱型梁极限承载性能的影响，本次实验共包括B-1S、B-2S、B-1D、B-2D等4个模型。4个模型的剖面尺度相同，模型名称中的H表示该模型由高强钢制作，S表示其循环载荷模式为单向循环，D表示循环载荷模式为双向循环（即载荷在循环过程中会发生方向的改变）。B-1S、B-1D与B-2S、B-2D的加强筋疏密不同。系列模型的横截面形式见图1，各模型的具体设计尺寸、材料属性及加强筋数目等见表1。模型所用钢材的极限性能由材料拉伸实验获得，具体情况可参见文献[13]。

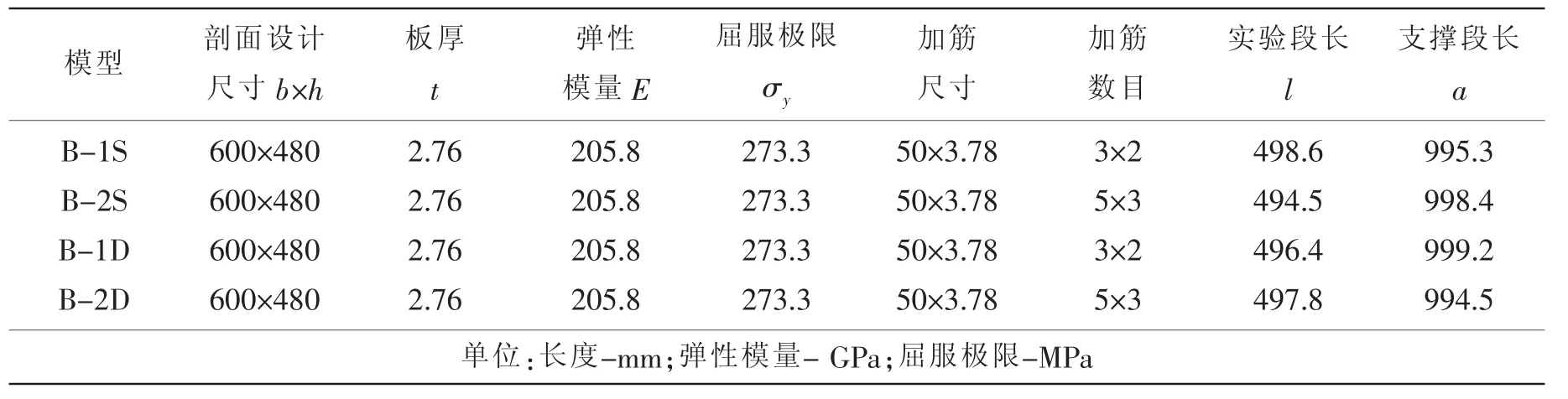
表1 箱型梁系列模型的设计参数与材料特性Tab.1 Design parameters and material behavior of the box-girder models

图1 箱型梁系列模型横截面形式Fig.1 Cross section of the box-girder models

1.2 循环载荷下系列箱型梁模型的加载系统及装配

本实验采用美国MTS动力加载实验与分析系统对实验模型进行循环弯曲加载。模型实验段和支撑段之间设置横隔板，将其作为实验段的边界。加载头外力由加载梁作用于横隔板上的两钢柱分配至箱型梁实验段两端，为避免箱型梁两端应力集中，两端也设置了横隔板。箱型梁模型实验装配见图2。

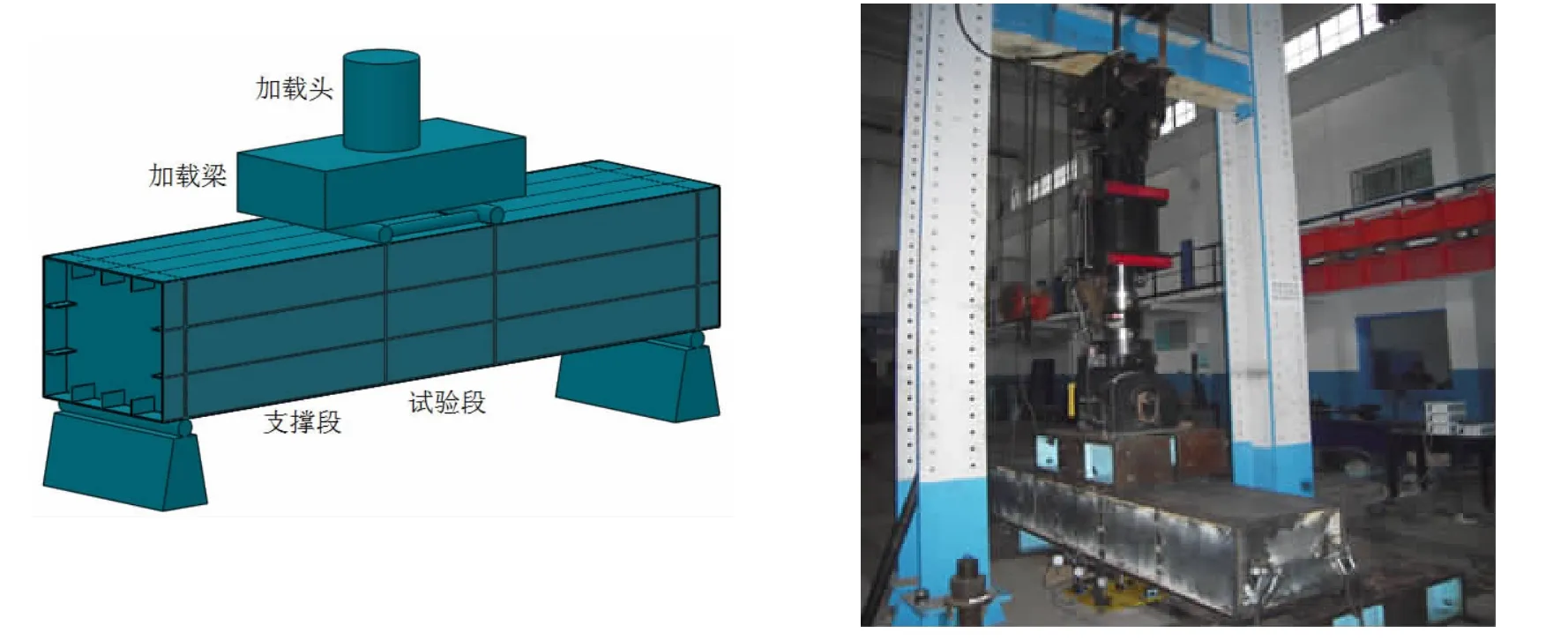
图2 箱型梁模型实验装配图Fig.2 The test set-up of box-girder models

1.3 循环弯矩下箱型梁系列模型的测量系统

循环弯曲实验中采用6台电子百分表，置于箱型梁实验段底部，实时测量实验段底部的垂向位移。位移测量点具体分布情况参见图3，d1、d3、d4和d6为横隔板与实验段底部交点垂向位移，d2、d5分别处于 d1、d3；d4和 d6中间。

图3 实验模型位移测量点分布图Fig.3 Displacement measurement points for box-girder models

2 箱型梁模型循环弯曲实验流程

由于箱型梁模型循环下的弯曲极限强度实验包含了多次的弯矩加载与卸载过程，因此加载过程中必须保证箱型梁在下一次循环开展前不产生过度的变形甚至崩溃。因此在载荷施加控制上，特别需要及时调整加载方式[13]。同时，在双向循环B-1D、B-2D实验的反向弯曲时，需要对箱型梁进行翻身，测量系统需要重新调整。具体实验流程如下：

第一步：加载系统、测量系统调试完毕后，首先对箱型梁模型进行多次小载荷反复加、卸载，充分释放模型焊接残余应力。

第二步：开始正式加载。在加载初始阶段施加的载荷较小，此时加载系统采取力控制、位移保护加载策略；当载荷接近箱型梁的极限载荷的前后附近阶段，实验段出现明显的塑性变形、且有快速扩展趋势时，加载系统调整为位移控制、力保护加载策略。此加载方式可避免方柱模型在极值点附近崩溃，导致后续实验无法开展。

第三步：当箱型梁达到所需的变形及载荷要求后，MTS加载头停止加载，并逐步抬升，完成卸载。卸载过程中，采取力控制、位移保护卸载策略。对B-1S，B-2S单向循环弯曲实验模型，在卸载完成后，可以重新进行第二步操作。对B-1D，B-2D双向循环弯曲实验模型，在每次卸载完成后，都需要进行上下翻身来进行反向加载。翻身后调整测量系统，再进行第二步操作，直至所有循环结束。

第四步：实验结束后，检查箱型梁最终破坏形式与变形情况。

3 循环弯曲实验中箱型梁模型失效与变形

所有模型在每次循环载荷施加初期，实验段构件变形及崩溃缓慢发展，当箱型梁处于承载能力发生削弱的后极限强度阶段时，实验段变形及崩溃速率明显加快，此时必须对MTS系统采取位移控制手段，以免过度变形损坏模型。在单向弯曲循环时，箱型梁B-1S实验段上顶部受压屈曲，下底部承受拉伸变形。上顶板部位的塑性变形及端面转角是单向增加的，且屈曲区域由上顶部向两侧由上至下扩展。在双向弯曲循环中,箱型梁B-1D，B-2D实验段在每次循环卸载结束后，都要翻身进行重新加载，在每次重新加载初期，由于反向载荷的作用，上一次循环产生的变形有小量抵消。随着载荷的增加，实验段的转角先减小后反向增加。实验结束后，上顶板和下底板的塑性变形趋于均匀，两侧构件的塑性变形较单向循环分布范围更大。B-1S，B-1D，B-2D实验段实验结束后的变形见图4-9。

图4 B-1S箱型梁实验段顶部变形Fig.4 Deformation on the top(B1-S)

图5 B-1S箱型梁实验段侧面变形Fig.5 Deformation on the side(B1-S)

图6 B-1D箱型梁实验段顶部变形Fig.6 Deformation on the top(B1-D)

图7 B-1D箱型梁实验段侧面变形Fig.7 Deformation on the side(B1-D)

图8 B-2D箱型梁实验段顶部变形Fig.8 Deformation on the top(B2-D)

图9 B-2D箱型梁实验段侧面变形Fig.9 Deformation on the side(B2-D)

4 循环弯矩下系列箱型梁模型实验数据处理

系列箱型梁模型的外力-位移曲线（P-δ）见图10-13，B-1S，B-2D两箱型梁的弯矩-曲率曲线（M-φ）见图14～15。P-δ曲线纵坐标P代表加载头所施外力，横坐标δ表征实验段的垂向位移；M-φ曲线纵坐标M代表实验段承受的纯弯矩，横坐标-表征实验段端面的转动曲率。δ，M，φ分别按以下表达式换算：

其中

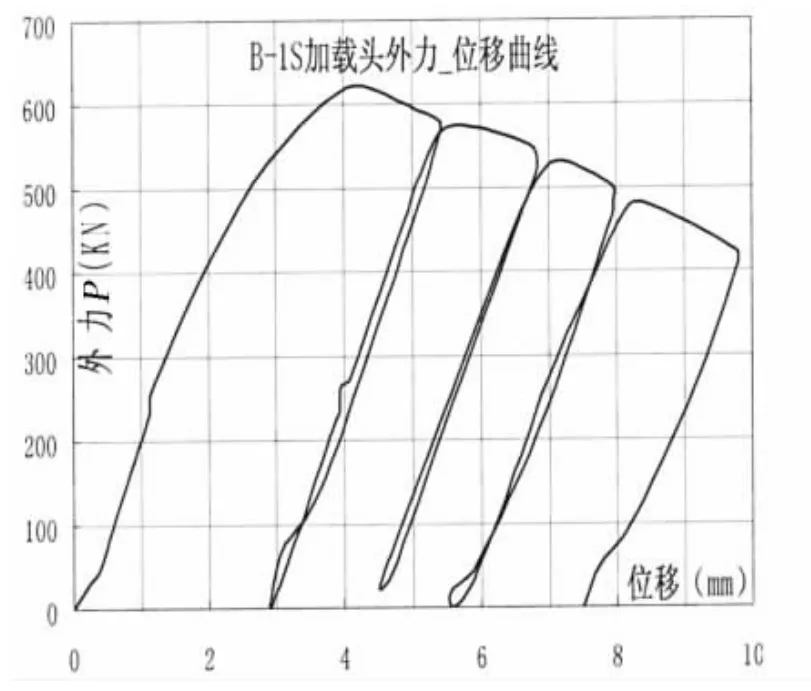
图 10 B-1S 外力-位移（P-δ）曲线Fig.10 Force-Displacement curve(B1-S)

图 11 B-2S 外力-位移（P-δ）曲线Fig.11 Force-Displacement curve(B2-S)

图 12 B-1D 外力-位移（P-δ）曲线Fig.12 Force-Displacement curve(B1-D)

图 13 B-2D 外力-位移（P-δ）曲线Fig.13 Force-Displacement curve(B2-D)

图 14 B-2D 弯矩-曲率（M-φ）曲线Fig.14 Moment-Curvature curve(B2-D)

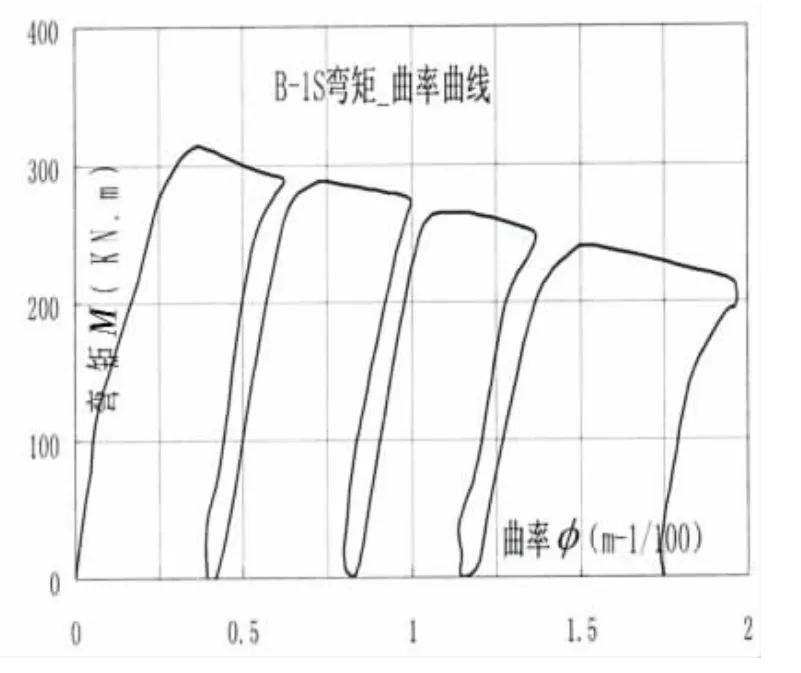
图 15 B-1S弯矩-曲率（M-φ）曲线Fig.15 Moment-Curvature curve(B1-S)

5 结 论

本文设计了B-1S、B-2S、B-1D、B-2D等系列箱型梁，并开展了单向及双向循环弯曲载荷下的极限承载性能实验。通过实验获取了模型的外力-位移（P-δ）曲线，弯矩-曲率（M-φ）曲线。经过对实验结果的分析，得到了以下结论：

（1）通过合理采取动力加载系统的载荷施加模式，既保证了实验中的加载效率，又避免造成模型的过度变形而急剧崩溃、使得后续实验不能开展。实验结果表明本文所采取的实验方案和实验技术是可行的。

（2）实验表明箱型梁在承受循环载荷初期，其构件崩溃速率较缓，而一旦进入后极限阶段，崩溃速率显著加快，此时必须采取位移保护措施避免模型变形过大。单向循环实验中，屈曲部位的面外挠度随循环次数的增加而增加，屈曲部位由上至下向两侧扩展。双向循环实验时，塑性变形由于反向弯曲的施加得到了部分抵消，但是屈曲的范围分布更大。

（3）从实验结果的曲线图中可以看出，单向循环弯曲实验中，模型后续循环的极限强度与前一循环后极限强度阶段的卸载点接近，但塑性变形以及实验段端面残余转角随循环次数的增加而增加，表明箱型梁的抗弯刚度由于塑性变形及塑性区域的扩展，其抗弯刚度发生了削弱。

（4）双向循环时，虽然反向弯曲抵消了部分塑性变形，但箱型梁模型的极限承载能力仍有明显下降。需要提及的是，B-1D箱型梁模型在双向循环实验过程中，其上顶部加筋板在较大的压缩-拉伸循环载荷作用下，第三次循环时板材撕裂，导致后续实验中止。

（5）开展循环载荷下船体结构的极限强度研究，对海洋环境中的实际承受循环载荷的船体结构的极限承载能力的准确评估具有十分重要的意义。为了研究的深入和进一步推进，应该从理论分析、数值模拟和模型实验等方面进一步深入开展相关研究工作。

[1]Gordo JM,Soares CG.Approximate methods to evaluate the hull girder collapse strength[J].Marine Structures,1996,9(3-4):449-470.

[2]Rahman M K,Chowdhury M.Estimation of ultimate longitudinal bending moment of ships and box girders[J].Journal of Ship Research,1996,40(3):244-257.

[3]Paik JK,Kim B J,Seo JK.Methods for ultimate limit state assessment of ships and ship-shaped offshore structures:Part III hull girders[J].Ocean Engineering,2008(35):281-286.

[4]ISSC CommitteeⅢ.1 Report:Ultimate strength[C].Proceedings of the 18th International Ship and Offshore Structures Congress(ISSC),2012:285-363.

[5]黄震球,陈齐树,骆子夜.循环弯曲载荷下船体梁的极限纵强度[J].中国造船,1996(3):87-95.Huang Zhenqiu,Chen Qishu,Luo Ziye.Ultimate longitudinal strength of ship’s hull girder under cyclic bending loads[J].Shipbuilding of China,1996(3):87-95.

[6]Xu Weijun,Iijima K,Wada R,Fujikubo M.Experimental evaluation of the post-ultimate strength behavior of a ship's hull girder in waves[J].JMarine Sci.Appl.,2012,11:34-43.

[7]丁 超,赵 耀.船舶总纵极限强度后剩余承载能力有限元仿真方法研究[J].中国造船,2014,55(1):54-65.Ding Chao,Zhao Yao.Simulation of ship residual carrying capacity after longitudinal ultimate strength[J].Shipbuilding of China,2014,55(1):54-65.

[8]Reckling K A.Behavior of box girders under bending and shear[C]//Proc.of ISSC’79.Paris,1979,II:2.46-2.49.

[9]Ostapenko A.Strength of ship hull girder under moment,shear and torque[C]//Proc.of Symp.Extreme Loads Response.Arlington,Virginia,U.S.A.,1981:149-166.

[10]Nishihara S.Analysis of ultimate strength of stiffened rectangular plate[J].J of the Soc.Of Naval Arch.of Japan,1983,154:367-375.

[11]Mansour A E,Yang JM.Thayamballi A.An experimental investigation of ship hull ultimate strength[J].Trans.SNAME,1990,98:411-439.

[12]Fukumto Y,Kusama H.Cyclic bending tests of thin walled box beams[J].Proc.of JSCE.Structural Eng.Earthquake Eng,1985,2(1):141-151.

[13]Yang P,Cui H,Dai Y,Zhou L.Experimental and numerical investigations on ultimate strength of ship plates under longitudinal cyclic loads[J].Journal of Ship Mechanics,2014,18(9):1100-1108.