自升式平台管结构碰撞损伤机理研究

刘 昆，高明星，俞同强，王自力

（江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003）

0 引 言

深海自升式海洋平台作为海上油气资源开采的主要工具，如果与船舶发生意外碰撞事故，会造成海洋平台结构损伤甚至失效，带来巨大的经济损失和不良的社会影响，甚至造成不必要的人员伤亡和海洋环境污染。数据库WOAD（1996）中统计了海洋平台发生的意外事故，主要发生的事故类型有碰撞、井喷、结构损伤等[1]。因此，开展深海自升式海洋平台的碰撞性能研究，揭示平台结构在意外撞击载荷作用下的损伤变形机理，对更好地开展平台耐撞结构设计有重要的现实意义。

自升式平台所面临的主要威胁来自守护船舷侧的碰撞，所以其桩腿管结构受侧向冲击载荷的变形机理成为本文的研究重点。目前采用的研究方法主要有模型试验法、简化解析计算法和数值仿真法。其中试验法是研究管结构强非线性动态响应的最可靠方法，Cho等[2]通过开展管结构模型试验，研究了其在低温条件下，受侧向载荷时的变形特点；刘昆等[3]以自升式平台桩腿直管为研究对象，开展了管结构落锤冲击模型试验，探究不同冲击速度下管结构的变形特征。由于解析计算方法既可以迅速地给出所需的解析表达式，又可以提供较好的分析结果，故在管结构碰撞领域得到了广泛的应用。其中Wierzbicki和Suh[4]提出了圆管在侧向线载荷作用下的变形模式，并推导出各种边界条件下的碰撞力与撞深之间的解析表达式；李若轩[5]以导管架平台上倾斜圆形管柱为研究对象，提出了两端固支管结构在倾斜面载荷撞击下的变形模式，给出了管结构能量耗散的解析表达式。由于管结构碰撞试验属于成本较高的破坏性试验，而且实际碰撞条件具有不确定性，使数值仿真成为分析该类强非线性碰撞问题的重要手段。其中Wierzbicki和Sinmao[6]利用ABAQUS有限元软件对圆管在塑性弯曲中的Brazier效应进行了研究。丁红岩[7]以船舶与立管碰撞为研究对象，采用显式有限元法模拟碰撞过程，得到立管碰撞力、结构响应及损伤变形等一般性规律。

本文以平台桩腿管结构为研究对象，采用简化解析法和数值仿真法研究其在侧向冲击载荷作用下的载荷挠度特性。文中首先提出了一种符合真实情况的管结构塑性变形模式，并利用刚塑性理论和塑性铰线理论，求出碰撞力与撞深之间的解析表达式；然后利用有限元软件ABAQUS对管结构在碰撞过程中的动态响应进行仿真计算，得到了管结构的载荷挠度特性，并将仿真结果解析计算结果对比，验证本文解析方法的正确性。

1 自升式平台管结构碰撞解析研究

1.1 管结构变形模式及特征

基于前期冲击试验和数值仿真研究，在侧向冲击载荷作用下，两端刚固的管结构主要发生局部凹陷和整体弯曲变形。本文研究的管结构发生小挠度变形，为了简化解析计算，假设管结构不发生整体弯曲塑性变形，如图1所示。

本文提出的管结构的变形模式是基于以下假设提出的：

（1）材料模型是理想刚塑性模型；

（2）将冲击载荷简化为线载荷，则管结构跨中凹坑的吸能可忽略不计，同时认为局部碰撞影响区域的长度是有限的，是加载过程中的变量，用ξ表示，如图2所示；

（3）假设管结构的横截面均由一系列直线和圆弧组成，直线与圆弧之间和圆弧与圆弧之间由塑性铰连接，如图3所示；

（4）假设在塑性变形区域，所有的横截面只发生刚体平移和旋转，且不存在抗剪；在管的变形影响区之外，不存在管的畸变和翘曲。

由能量守恒可知，外部和内部能量耗散率相等：

由于管结构只受集中荷载P，故：

图1 管结构的受力图Fig.1 Diagrams of pipe structure suffering the force

本文采用Wierzbicki和Suh[6]的研究方法，将内部能量分为横截面方向和轴线方向的能量，即满足：

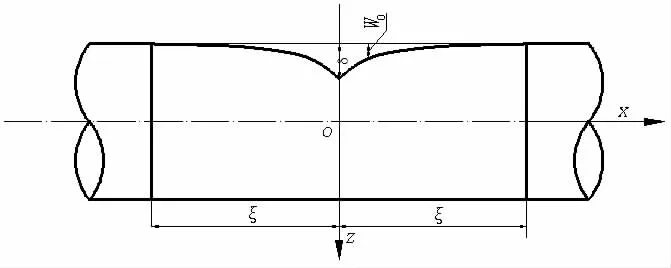
图2 轴向的变形模式Fig.2 The deformation mode of axial direction

图3 横截面方向的变形模式Fig.3 The deformation mode of cross section direction

1.2 横截面方向的能量耗散

在横截面方向，凹陷区域内管结构吸收的塑性能包括两项：圆管上表面由圆柱面变为平面及下表面曲率变化吸收的能量E1，塑性铰线转动所吸收的能量E2。因此，利用虚功率原理，管结构横截面方向的总能量耗散率可表示为：

本文假设变形后圆管横截面的周向长度不变，根据图3，可得以下几何关系：

其中为下铰链的位置。

其中：V1和V2是两个塑性铰的切向速度。

圆弧曲率的变化率可通过对相应圆弧曲率求导得到，结果为：

将（6）、（7）式和（8）式代入（4）式中可得：

根据图3，撞深δ用R1、R2和φ表示如下：

本文视撞深为自变量，则（5）式和（10）式中四个参数可以消掉两个，为了描述管结构变形的问题，仍需建立一个涉及以上参数之间关系的方程。由于无因次半径（R2/ ）R 在变形的过程中递减，且当φ=时）取初始值1，故本文认为 （R2/R ）与 φ 之间存在一定的函数关系，如下：

其中：铰链起始位置φ0和参数n是待定的常数。

根据解析理论，管结构横截面方向的能量耗散率还可用瞬时破碎力Pc（wc）和跨中速度的乘积表示：

当和 π 时，联立以上方程组，通过使用 Matlab 数学软件，可以画出无量纲量 Pc/（4M0/ ）R 与δ/R之间的函数关系，见图4。

因为管结构只是单侧受力，变形模式是不对称的，用参数φ0=π/2和n=1描述管结构的变形是合理的。同时据图4可知，出于简化目的，当δ/R≤1时可认为破碎力Pc是恒定的：

由于本文认为管结构轴线方向由一系列无关的刚塑性梁元组成，基于刚塑性梁的大变形分析[8-9]，可以假设首要梁柱的速度场随x线性变化，可得：

其中：x=ξ时是瞬时旋转点。联立以上方程，可求得凹陷区域的总破碎能量：

图4 n=1时单个圆环破碎强度的无因次量与撞深之间的关系Fig.4 Relationship between the dimensionless quantity of the crushing strength and the collision depth when n=1

1.3 轴线方向的能量耗散

塑性梁元发生弯曲变形和拉伸变形，但是由于梁元纵向曲率的变化要比圆环环向曲率的变化要小得多，可认为塑性梁元为刚性梁，只发生拉伸变形，则可得管结构轴线方向的能量耗散率：

其中：N0=σ0t是单位宽度梁元上的完全塑性薄膜力为轴向总应变率。

经简化后的管结构只发生凹陷变形，则仅由其局部凹陷变形引起，定义如下：

参照（13）式，认为所有梁元的速度均随x线性变化，则角α处梁元的速度场可表示为：

其中：为角α处梁元的跨中速度。

则单个梁元对能量耗散率的贡献变为：

Suh[10]研究了由凹陷变形的应变率与无因次量 α/π 的函数关系，提出了一种近似计算应变率的表达式：

联立（15）、（18）式和（19）式可得轴线方向的能量耗散率：

1.4 载荷挠度特性

由外部和内部能量耗散率相等得：

消去上式两边的相同项：

上式的中心参数有两个，对上式应用上限定理，求偏导∂P/∂ξ=0，可得ξ和δ之间的关系：

将（23）式代入（22）式中可得两端固支管结构在侧向冲击载荷作用下的载荷挠度特性：

从上式可以看出，碰撞力与材料的平均流动应力线性相关，与管结构的径厚比和非线性化后的撞深成平方根关系。

材料的流动应力在一定程度上度量了管结构抵抗塑性和弹性破坏的能力，因此为了保证解析所得碰撞力与试验测定的碰撞力一致，必须对其正确的取值。通过参考相关国内外文献[11-12]，并结合本文管结构的材料特性，流动应力定义如下：

其中：σs为材料的屈服极限，σb为材料的强度极限。

2 自升式平台管结构碰撞仿真研究

2.1 有限元碰撞模型的建立

本文研究的是船舶与自升式平台桩腿管结构的局部碰撞，为了便于模拟管结构受侧向载荷时的动态响应，需要对碰撞系统进行简化，其中将撞击船简化为三角楔形刚性锤头，被撞桩腿简化为两端固支的直管结构。为了保证管结构两端刚性固定的边界条件，在管结构试件两端各焊接一个端板，同时在每端用4个肘板进行加固。管结构模型的具体尺寸见表1，用ABAQUS建立的有限元模型如图5所示。

图5 有限元模型Fig.5 Finite element model

表1 有限元模型几何尺寸汇总表Tab.1 Summary of the geometric size of the finite element model

2.2 材料参数的设置

管结构的材料是船用钢Q235，其材料力学性能由准静态拉伸试验获得[13]，见表2。由于本文管结构的碰撞响应是动态的，涉及到材料在动载作用下的本构关系，因此为了提高计算的准确性，需要考虑应变率敏感效应[14]。本文选用Cowper-Symonds应变率强化模型，其公式为：

其中：σy为动载应力值；σx为静载应力值，可由准静态拉伸试验获得；ε˙为应变率；D和P是与材料相关的参数，就低碳钢 Q235 而言，D=40.4，P=5[15]。

表2 船用钢基本力学性能参数Tab.2 Mechanical parameters of marine steel

本文研究的是管结构的内部变形机理，锤头的变形和吸能可忽略，故可将锤头模型简化为刚体。

2.3 网格的划分

本文管结构模型选用4节点四边形缩减积分板壳单元，即S4R；锤头模型选用四节点三维线性刚体单元，即R3D4。在控制沙漏产生的基础之上，同时兼顾工程精度和计算工作量，选用全局尺寸10 mm的网格进行仿真分析。

2.4 约束条件和外载的确定

创建接触属性时，对于接触面之间的切向作用，本文选用库伦摩擦模型，摩擦系数为0.3；对于法向作用，选硬接触（“HARD”Contact）。为了实现管结构两边刚固的条件，对管结构模型端板上的圆孔施以刚性固定，同时锤头模型仅保留自由落体方向的自由度。

本文锤头质量设为1 420 kg，能满足管结构的中低速碰撞要求，同时落锤的下落高度分别设为1 m、2 m和3.6 m，共三种工况，相应的冲击速度为4.43 ms-1、6.26 ms-1和8.40 ms-1。

3 仿真与解析的对比

本文所采用的数值仿真技术的可靠性在文献[3]中已经得到了试验的验证，这里将不再进行这方面的验证工作。

3.1 碰撞力—撞深曲线

图6为三种冲击高度下管结构在仿真和解析中所得碰撞力—撞深曲线对比图。通过比较可得：

图6 解析与仿真所得碰撞力—撞深曲线对比Fig.6 Comparison of the force-depth curve between analysis and simulation results

（1）在管结构发生塑性破坏之前，仿真方法中的碰撞力依次经历振荡、稳定加载及卸载三个阶段，而解析计算中的碰撞力自始至终只处于加载阶段，这是因为解析计算的模型是刚塑性模型，管结构只发生塑性变形。

（2）相同撞深下，解析计算所得碰撞力低于数值仿真所得相应值，这主要是由于在解析计算中忽略了整体位移对抵抗管结构变形的贡献，对于中低速碰撞，这种误差可以通过增加修正系数进行修正。

（3）当碰撞力处于加载阶段时，两种方法所得曲线的变化趋势相对一致，为给快速求出管结构处于加载末段的极限载荷提供精度证明。其中当冲击高度为2 m时，两种曲线吻合最好，几乎以相同斜率稳定增加；当冲击高度为1 m时，解析所得曲线的斜率大于仿真，这是因为较小冲击高度下管结构发生的变形不明显，仿真中碰撞力处于加载阶段的时程较小；当冲击高度为3.6 m时，解析所得曲线的斜率小于仿真，这是因为冲击能量较高，仿真中碰撞力处于加载阶段的时程较长，碰撞力增长较快。

综上所述，管结构在侧向冲击载荷的作用下，用简化解析计算方法所得的碰撞力-撞深关系具有一定的准确性和可靠性。

4 结 论

本文以自升式平台桩腿直管结构为研究对象，采用解析法和数值仿真法对其在侧向冲击载荷作用下的载荷挠度特性进行了研究，主要研究结论如下：

（1）分析解析计算所得管结构载荷挠度特性，可知碰撞力与材料的平均流动应力线性相关，与管结构的径厚比和非线性化后的撞深成平方根关系。

（2）对比数值仿真和解析计算所得结果，可知当碰撞力处于加载阶段时，两种方法所得曲线的变化趋势相对一致，证明了本文简化解析计算的准确性。

[1]林 一.自升式钻井平台风险评估方法研究[D].哈尔滨:哈尔滨工程大学,2013.Lin Yi.Research on risk assessment method of Jack-up drilling unit[D].Harbin:Harbin Engineering University,2013.

[2]Cho SR,et al.Experimental and numerical investigations on the collision between offshore wind turbine support structures and service vessels[M].Collision and Grounding of Ships and Offshore Structures,2013:281-286.

[3]刘 昆,包 杰,王自力,等.自升式平台直管结构碰撞模型试验与仿真分析[J].舰船科学技术,2015(S1):103-109.Liu Kun,Bao Jie,Wang Zili,Wang Ge.Experimental and numerical analysis on the impact performance of pipe structures of offshore jack-up platform[J].Ship Science and Technology,2015(S1):103-109.

[4]Wierzbicki T.Indentation of tubes under combined loading[J].International Journal of Mechanical Sciences,1988,30(3-4):229-248.

[5]李若轩.导管架平台圆截面管柱在侧向撞击下的变形机理研究[D].上海:上海交通大学,2015.Li Ruoxuan,Hu Zhiqiang,Yang Song.Research on deformation mechanism for circular section columns of jacket platform under lateral impact scenario[D].Shanghai:Shanghai Jiao Tong University,2015.

[6]Wierzbicki T,Sinmao M V.A simplified model of Brazier effect in plastic bending of cylindrical tubes[J].International Journal of Pressure Vessels and Piping,1997,71(1):19-28.

[7]丁红岩,乐从欢,张浦阳.双层立管在船舶撞击作用下结构行为分析[J].船舶力学,2010,14(8):894-900.Ding Hongyan,Le Conghuan,Zhang Puyang.Structural behavior analysis of the pipe-in pipe riser subjected to vessel impact[J].Journal of Ship Mechanics,2010,14(8):894-900.

[8]Parkes E W.The permanent deformation of a cantilever struck transversely at its tip[J].Proceedings of the Royal Society A,1955,228(1175):462-476.

[9]Hopkins H G.On the behavior of infinitely long rigid-plastic beams under transverse concentrated load[J].Journal of the Mechanics&Physics of Solids,1955,4(1):38-52.

[10]Suh M S.Plastic analysis of dented tubes subjected to combined loading[J].Ocean Engineering,1985:1-12.

[11]R/RH/R6-Revision 3.Assessment of the integrity of structure containing defects[M].Nuclear Electric Maintained Document,1994.

[12]BSI PD 6493.Guidance on the method for assessing the acceptability of flows in fusion welded structures[S].1991.

[13]包 杰.自升式海洋平台碰撞模型试验技术研究与应用[D].镇江:江苏科技大学,2016.Bao Jie.Research and application on model test technology of Jack-up platform collision[D].Zhenjiang:Jiangsu University of Science and Technology,2016.

[14]刘 昆.不同船艏撞击下船体结构碰撞性能研究[D].镇江:江苏科技大学,2009.Liu Kun.Study on the influence of striking bow shape to the side structure during ship collision[D].Zhenjiang:Jiangsu University of Science and Technology,2009.

[15]王自力,顾永宁.应变率敏感性对船体结构碰撞性能的影响[J].上海交通大学学报,2004,34(12):1704-1707.Wang Zili,Gu Yongning.Effect on strain-rate sensitivity on the behavior of ship structure in collision[J].Journal of Shanghai Jiaotong University,2004,34(12):1704-1707.