初中数学“综合与实践”活动的分类与实施建议*
——基于南京市的实施现状
“综合与实践”活动涵盖了整个数学课程,它穿插在“数与代数”“图形与几何”“统计与概率”等内容之中。“综合与实践”活动需要利用以上三大板块的知识,解决具有综合性与实践性的问题,在此过程中可能会涉及代数、图形、统计等多方面的知识,很多时候还需要利用物理、化学等其他学科的知识。通过“综合与实践”活动,学生能够解决富有挑战性的问题,积累丰富的数学活动经验,同时也能更深刻地体会数学的本质,切身感受数学与现实生活的紧密联系,从而培养学生的问题意识、应用意识、创新意识以及综合运用有关知识解决问题的能力。
我国的数学课程改革自20世纪90年代以来一直倡导培养学生的问题意识和应用意识,倡导改变学生被动学习的状态,培养学生发现问题和提出问题的能力。直到2001年颁布的《全日制义务教育数学课程标准(实验稿)》第一次将“实践与综合应用”作为单独的内容领域列入其中,以“课题学习”方式呈现(初中阶段),并且旗帜鲜明地指出:“‘实践与综合应用’将帮助学生综合运用已有的知识和经验,经过自主探索和合作交流,解决与生活经验密切联系的、具有一定挑战性和综合性的问题,以发展他们解决问题的能力。”[1]当时教材中好用实用的“实践与综合应用”活动素材还非常少,在国内比较系统的活动素材当属2008年由杨裕前、董林伟组织编写的《数学综合与实践活动》(江苏科学技术出版社,2008)。
2011年颁布的《义务教育数学课程标准(2011年版)》再一次将其作为单独的内容领域列入其中,将名称确定为“综合与实践”,并明确指出“综合与实践”的教学活动应当保证每学期至少一次,同时指出“‘综合与实践’是一类以问题为载体,以学生自主参与为主的学习活动”。在素材开发方面,2013年董林伟再次担任主编,组织编写《数学实验手册》(江苏科技出版社,2013)。
纵观初中数学“综合与实践”活动的发展历程,从“实践与综合应用”到“综合与实践”,从标准制定到教学实施,数学界的同仁一直在努力实践,尤其是江苏省的《数学综合与实践活动》与《数学实验手册》为广大教师开展“综合与实践”活动提供了很好的抓手。然而,在具体实施过程中依然存在这样或那样的问题。例如:由于中考在“综合与实践”活动方面设置试题的局限性,导致教师在开展相关课题研究方面积极性不高,教学研讨氛围尚未形成;目前南京市各初中学校生源差距较大,“综合与实践”活动在生源较好的学校基本上能得到保障,但生源基础薄弱的学校却几乎不开展此类活动,各学校开展的状况极不平衡;结合课本内容自主开发的“综合与实践”活动类素材缺乏,素材的有效性研究尚处于空白阶段;初中数学“综合与实践”活动课的设计与实施目前基本停留在“为活动而活动”的阶段,对其有效性研究甚少等等,诸如此类的问题大量存在。
基于以上对目前南京市初中数学“综合与实践”活动现状的分析,2016年以来,由何炳均和朱建明两位特级教师领衔的“初中数学‘综合与实践’活动的有效性研究”的课题组,先后开设了“探寻勾股数”“温度计上的一次函数”“探索四边形全等的条件”等7节市级公开示范课,开设了初中数学“综合与实践”活动课的设计思考、初中数学“综合与实践”活动评价思考、初中数学“综合与实践”活动课素材选择思考等7次市级专题讲座。这些活动展示了课题组对“综合与实践”活动资源的分类与开发的有效性、教学设计与实施的有效性、校本推进措施的有效性等方面的研究与探索,提高了初中数学“综合与实践”活动开展的实效性,对全市初中数学“综合与实践”活动的开展起到了辐射和引领的作用。下面笔者结合课题组的研究和自身的教学实践谈谈“综合与实践”活动的基本类型与实施建议。
一、初中数学“综合与实践”活动的基本类型
初中数学“综合与实践”活动形式是多种多样的,素材开发的途径和类型也是丰富多彩的。这些活动基本都具有综合性或实践性的显著特征,所关注的问题可能来自数学内部,也可能来自现实生活。
根据初中数学“综合与实践”活动的内容,目前大致可以分为“数学问题探究”“实际生活应用”两大类型,但随着初中数学“综合与实践”活动资源的深入开发,相信还会有更多类型的活动出现。
1.数学问题探究型。
这类活动一般情况下会以某个数学内部问题为主线,让学生进行自主探究。这一过程中要关注学生是如何探究、如何提出相关的数学问题以及如何深入分析数学问题的。我们课题组对苏科版初中数学教材中的“综合与实践”活动内容进行了梳理,其中数学问题探究型活动有:七年级上册中的“算24”“月历中的数学”,七年级下册中的“拼图·公式”“算年龄”“分类·想象·找规律”,八年级上册中的“关于三角形全等的条件”“折纸与证明”“探寻勾股数”“有关实数的课题研究”“关于勾股定理的研究”,八年级下册中的“摸球试验”“分式游戏”“画画·算算”,九年级上册中的“图形的密铺”“估测时间”。
2.实际生活应用型。
此类活动主要指面对身边的实际问题,通过分析和抽象,将其提炼为一个数学问题,然后进行分析直至解决,最终回到实际生活。常见的实际生活应用型“综合与实践”活动有数学建模、数学调查、数学操作等。
数学建模是指对实际问题进行简化,抽象,建立模型,求解,解释验证,从而解决实际问题。苏科版初中数学教材中的“数学建模”型活动有:七年级上册中“一元一次方程应用的调查”,七年级下册中的“一元一次不等式问题的调查”,八年级上册中的“温度计上的一次函数”。
数学调查是指学生在实践活动中收集数据、整理数据、描述数据,进一步分析数据,从而解决实际问题。教材中“数学调查”型活动大致有:八年级下册中的“丢弃了多少塑料袋”“心率的调查”,九年级上册中的“收集数据、分析数据、探索规律”,九年级下册中的“香烟浸出液对种子发芽的影响”等等。
数学操作是指学生动手设计或制作一些方案或作品,从而解决实际问题。数学操作能很好地锻炼学生的动手能力和想象能力。教材中“数学操作”型活动大致有:七年级上册中的“设计包装纸箱”“测量距离”“制作无盖的长方形纸盒”,七年级下册中的“利用平移设计图案”,八年级上册中的“确定藏宝地”,八年级下册中的“设计对称图形”,九年级上册中的“矩形绿地中的花圃设计”,九年级下册中的“校园景观设计”“测量两地间的距离”“测量建筑物的高度”“制作动画片”等等。
二、开展初中数学“综合与实践”活动的实施建议
1.注重“综合性”。
“综合与实践”活动实施的关键是如何让学生综合运用所学知识解决实际问题,在教学过程中要注重数学内部知识之间的联系、数学与外部生活的联系以及数学与其他学科的联系等。因此,“综合与实践”活动主题大都来自实际生活,对学生综合知识以及其他学科知识的整合能力要求较高。2015年12月课题组成员面向全南京市开设了一节“综合与实践”研讨课《温度计上的一次函数》。
案例1:温度计上的一次函数
活动1:阅读资料了解两种温度。
华氏度(Fahrenhite)和摄氏度(Celsius)都是用来计量温度的单位。了解华氏和摄氏这两种温标的具体标准。
活动2:分组探究两种温度之间函数关系。
观察温度计上两种刻度的关系,采集数据并填表。然后画图,观察,猜测,求解,验证。最后形成结论:F是T的一次函数,函数关系式为F=1.8T+32。
活动3:寻找生活中“温度计”式的一次函数。
你还能找到生活中“温度计”式的一次函数吗?
思考:用一支无刻度的温度计测冰水混合物,用刻度尺量液柱,为3厘米;用来测沸水的温度时,液柱为28厘米;如果现在是8厘米,那现在的温度是多少?
本节“综合与实践”活动课旨在探究两种温标之间的函数关系。在探索过程中,让学生尝试建立函数模型,并且感受一次函数在实际生活中的广泛应用,然后根据活动经验,进一步自主探究生活中“温度计”式的一次函数。在本节课的教学中,既有数学与生活实际的综合,又有数学内部知识方法的综合。
2.落实“实践性”。
“综合与实践”课的教学要注重学生的经验应形成于学生应用知识解决实际问题的实践活动中。因此,“综合与实践”活动必须突出实践性,让学生在实践的基础上,领悟数学本质。例如,2016年3月我们开设了研讨课《心率的调查》。
案例2:心率的调查
活动1:自主测量收集数据。
查阅资料了解心率。分正常的成年人、新生儿、2~4岁儿童三类。
将全班学生分成若干个小组,每组5人左右,以心率为主题自选调查内容,确定适当的统计调查方法,收集数据。
活动2:小组合作处理数据。
每一小组将收集到的数据按照小组内部确定的方式进行处理,用适当的方法描述,并进行多角度的分析。
活动3:课堂展示分享交流。
(1)研究展示:小组展示(展示具体材料略)。(2)请各组谈谈自己课前了解到的心率的相关知识。(3)实践尝试:现场测脉搏。
本课要求学生先“自主测量,收集数据”,这一过程非常好地体现了“综合与实践”活动课的“实践性”的本质要求。因此,在“综合与实践”活动过程中一定要引导学生亲身实践,小组合作制作统计表、统计图来描述数据。在本节课的教学中,教师在课堂内外为学生提供了大量自主探究、动手实践、合作交流、展示汇报的机会,引导学生在“用数学”的过程中,积累数学活动经验,提高学生解决实际问题的能力。
3.凸显“问题”性。
“综合与实践”活动开展的过程中应以问题为中心,问题既是活动的出发点,也是活动的归宿,通过设置问题串和层层追问,逐步引导学生探究数学的本质。2016年5月课题组又开设了研讨课《探索四边形全等的条件》。
案例3:探索四边形全等的条件
活动1:画全等四边形。
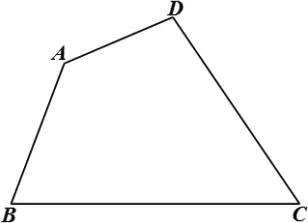
如左图所示,已知四边形ABCD,请你画出四边形DEFG,使它与四边形ABCD全等;
问题1:要使两四边形全等,至少需要几组元素对应相等?
活动2:思考如何分类。
问题2:两四边形中五组元素对应相等,可能会有哪些情况?
活动3:归纳类比拓展。
问题3:上述探索四边形全等的过程中你有哪些收获?你觉得该如何研究五边形全等?谈谈你的思路。
在本节“综合与实践”活动课的教学中教师始终以问题为主线展开教学,主问题是“两四边形具备怎样的条件才能全等”。类比以前的研究经验,进一步追问“至少需要几组元素相等就可以保证两四边形全等”。在探索过程中进一步提出问题“五组元素相等如何分类研究”,再引出拓展问题“五边形乃至n边形全等的条件如何探索”。本节课凸显活动的“问题”性,以问题串的形式构成了整个活动的逻辑暗线。
4.倡导“自主性”。
上好数学活动课的关键是让学生“自主”参与课堂。学生才是“综合与实践”活动的主体,而教师只需给予适当的点拨和指导。2015年10月课题组开设了研讨课《探索勾股数》。
案例4:探索勾股数
活动1:交流课前成果。
问题:小组内同学交流,比较各自收集、整理的勾股数,有什么疑问?
活动2:探寻勾股数。
1.观察表格,a、b、c是一组勾股数。
思考:(1)填写表格中的空格;
(2)在表中,a为大于1的奇数,正整数b和c之间的数量关系是 ,b、c与a2之间的关系式 。
(3)一般地,当 a=2n+1(n为正整数)时,请给出计算勾股数的一组公式。
(4)你能确定你给出的公式正确吗?证明你的结论。
活动3:构造勾股数。
任意写一个大于2的整数,你能写出另外两个数,使它们构成一组勾股数吗?
活动4:课外延伸。
对探寻“勾股数”有兴趣的同学,可以在网上查阅有关资料,收集构造勾股数的其他方法。
本节“综合与实践”活动课分三个阶段进行。第一阶段为课上探究做准备,也是探究前的热身。第二阶段是课中探究,釆取教师适时点拨,学生不断思考的方式进行。第三阶段为学有余力的学生提供后续探究的空间指明方向,明确任务,激发这部分学生的学习积极性,体现“不同的人在数学上得到不同的发展”这一数学育人理念。
[1]教育部.全日制义务教育数学课程标准(实验稿)[S].北京:北京师范大学出版社,2001.
[2]张伟俊.“综合与实践”课的教学探索与实施建议——以“探究最短路径问题”为例[J].中国数学教育,2015(06).
[3]王荣宝.初中数学“综合与实践”课程实施的校本研究——以南京市六合区竹镇民族中学为例[D].昆明:云南师范大学,2016.

