探究“圆”理,走进圆的世界
安徽省池州市东至县至德小学 胡根华
我和学生近期徜徉于圆的知识领域,不断总结学习方法和技巧,在摸索中前进。个人认为,通过这段时间的训练、指导,经历多次磨合,学生逐渐地感悟“圆”理,走进圆的世界。教师要做一个撒播种子的人,让学生充满期盼地迎接智慧的曙光。
一、巧用知识点,灵活记心间
1.熟记5个公式
要想学生较好地理解并掌握圆的有关知识,首先要熟记以下5个公式:
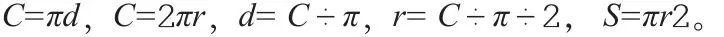
前两道是已知直径或半径求周长,第三道和第四道是已知周长求直径或半径,最后一道是圆的面积公式。学生仅仅熟记这几道公式还不够,要在审题的基础上灵活选择与运用,这样才能举一反三。
2.熟记计算结果
虽然教材上指出计算出的周长或面积结果可以直接用π表示,但习惯上我们仍然把π取近似值3.14表示。这样的话,要多次重复地计算关于3.14乘一个数,不仅浪费时间,而且错误率高。为了不耗时低效,我让学生熟记以下计算结果:(1)3.14乘1至10的结果;(2)3.14乘1至10的平方的结果;(3)3.14乘1.5至3.5的平方的结果
当把以上公式和计算结果都烂熟于心的时候,基础就扎实了,就为解决有关圆的问题做好了充分准备,而且省时高效。记得有学生说道:“老师,这样太方便了!我们愿意背,我们喜欢用。”我想,这也是我的初衷。
二、慧眼识真面,审题是关键
学了圆的知识,最多的就是求周长和面积,但孩子们特别容易混淆。我引导学生在很多的题例中发现、归纳与总结:如果是求给圆形桌子铺新的桌面是求面积,而给桌面镶上金边是求周长。题意明确了,方向就明确了,问题就迎刃而解了。
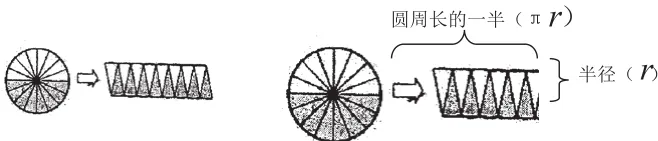
例如上图,是圆面积公式的推导过程。
学生经历了操作过程,但对其对应关系仍掌握得不透彻。我让孩子们在右面近似的长方形里标一标。这样,学生直观地看出:这个近似长方形的长等于圆周长的一半,宽等于圆的半径。并且长方形的周长大于圆的周长,增加的部分就是两条半径。再如,学生计算半圆的周长时经常出错,认为“半圆的周长=圆周长的一半”。为了提醒不要忽略“加上直径”,我让学生多次对着半圆比划,深刻地体会到“半圆的周长=圆周长的一半+直径”。
像上述情况还有很多,只有具备一双认慧眼,认真审题,才能不被表面现象所迷惑,深刻领悟本质,从而豁然开朗。
三、用好错资源,转型中提升
无论是平时的巩固训练,还是检验与测试,学生总难免出现各种各样的错误。而用好错误资源,可以让学生去反思,汲取教训,从而在反复的转型中得以提升思维。
例如,下图,图中正方形的面积是5平方厘米,你能求出圆形的面积吗?
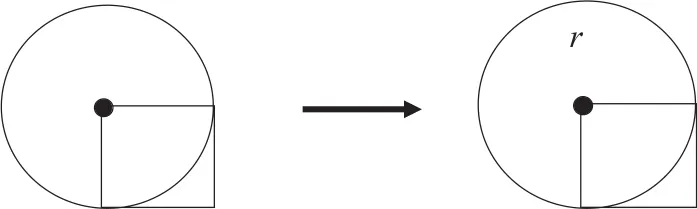
只要是求圆的面积,学生第一反应是“S=πr2”,那还不简单吗?算式为:3.14×52=78.5。但有的孩子着急了,质疑道:“5又不是圆的半径,所以算式是错的。”我追问:“对呀,那这道题是不是没办法解决了呢?”学生异口同声“不是!”后来引导时,我只是让学生像图4那样标上“r”。此时,学生争先恐后地抢答“老师,我知道了!因为这个正方形的边长就是圆的半径,边长×边长=半径×半径,即正方形的面积= r2,根据S=πr2,本题直接列式为:3.14×5=15.7”。
我想,此刻的学生真正经历了什么是“柳暗花明又一村”的喜悦。
圆的知识领域瑰奇而美丽,博大而精深。不经历一番思考,难以有深刻的认识,思维就难以提升。有时,换个角度想问题,变个思路去思考,才能感受到“曲径通幽”,也才能真正领略到数学的神奇。

