思维导图在初中数学中的应用

广东省广州市增城区第二中学 欧阳顺银

近年来，初中数学课堂出现了多种方式改革，无论什么方式的改革，都必须以学生个人知识的内在消化、思维的发展、能力的提升为目标。学生是学习的主体，授人以鱼不如授人以渔。掌握数学知识内容是初中数学课堂的主要任务。思维导图是实现学生掌握数学学习内容的有效学习方式。它利用图形将分散的数学知识通过图形把数学相关的知识点建立联系的图形，以树状图或者其他结构图形为其呈现方式，帮助学生更有效地学习数学，更清晰地呈现数学思维过程。数学知识形如分散，实为息息相关的。思维导图以直观形象的显示方式把无形的数学知识或者数学思维呈现，不但使学生“知其然”并且“知其所以然”。因此，思维导图与初中数学有着密切的关系，思维导图是一种初中数学思维表达工具。数学课程是以运用数学的思维方式进行思考为总目标之一。思维导图的制作更能促进学生的思维发展，提高学生的分析能力、推理能力、归纳演绎能力等数学素养的养成。本文通过思维导图在初中数学的预习、复习和练习题分析演绎讲解中的应用进行阐述。

一、思维导图在初中数学预习中的应用

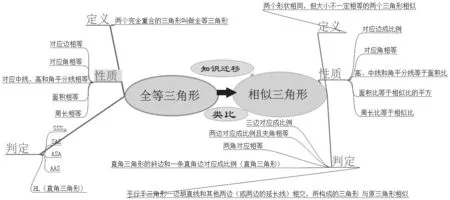
思维导图在初中数学预习中起到旧知识迁移、新知识生成的作用。教学前置活动中，教师通过利用思维导图让学生在预习的时候对已掌握相关的知识基础上进行知识的迁移，把旧知识和新知识之间的共通点通过思维导图联系起来，通过学生的回忆旧知识、思考新知识等无形的思维活动通过有形的导图描述起来。例如，如下图所示，在预习《相似三角形》的新知识中，学生可以通过已经学习的《全等三角形》知识，借助思维导图，把旧知识通过导图构建出来。学生通过构建思维导图过程，对新的知识《相似三角形》通过类比共性与区别生成相似三角形的定义、性质、判定等，同时对老师在课堂的讲解会有更深刻的认识，而学生本人在新知识上有了全面的思考分析过程，锻炼思维能力、提高推理能力，体会数学知识之间的联系。

二、思维导图在初中数学复习中的应用

初中数学内容章节知识虽多，但是知识之间又相互联系，章节之间，单元之间都相互联系。因此在教学活动中为了让学生对知识有整体的认识，教师可以通过思维导图工具把知识点要素罗列出来。

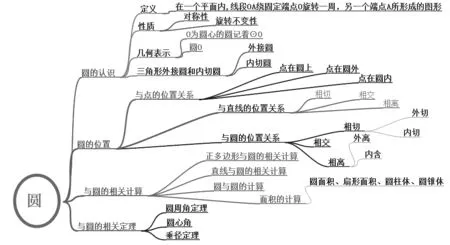
思维导图在初中数学中的复习应用可以从两方面考虑：一是中考整章复习。例如，在九年级中考数学复习中，对圆的综合复习，可以通过导图的制作将圆的知识内容进行整理，这样可以让学生回忆《圆》这章的知识点、结构，而且能够对知识有更深层的理解，同时又可以清楚知道自己的知识点掌握情况，“知其然并知其所以然”。让学生真正地全面复习，把知识渗透在导图中，也把问题清晰反映在导图中，学生制作的导图能准确反馈信息给教师，让教师明确知道学生的知识点掌握情况，做到有针对性地对知识进行回顾、复习。而学生也可以通过自己在制作导图的过程中发现自己对知识的遗漏情况，及时进行进一步的复习，真正使自己的复习效果达到高效。

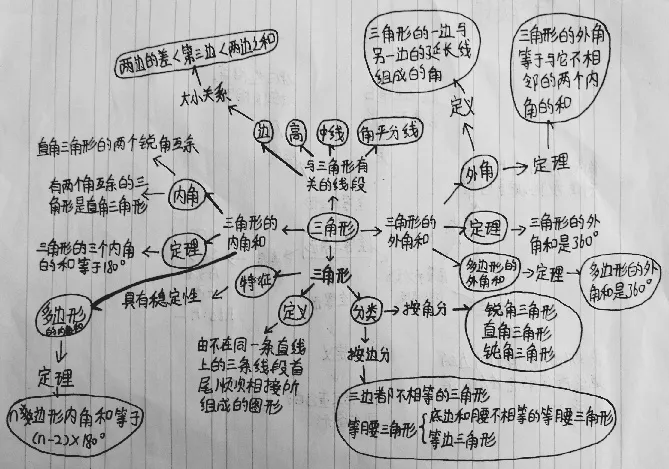
二是单元复习，如下图为学生自己制作的思维导图，虽然是手笔描绘，但是能够利用知识将本章节的《三角形》内容通过导图一一描述出来。学生可以加深对知识的理解，也可以清楚知道自己哪些知识点遗漏，那样就可以真正做到知识的查漏补缺。

三、思维导图在初中数学习题的演绎分析中的应用

初中数学以发展合情推理与演绎推理的能力为教学目标之一，作为一门理科学科，掌握解决数学问题的方法是非常重要的，而数学思维导图可以帮助学生分析题目，从学生分析的角度出发为学生疏通解题思路，提高学生的推理演绎能力。

如题：（如图1）已知正方形ABCD的对角线AC、BD相交于点O，E是AC上一点，连接EB，过点A作AM⊥BE，垂足为M，AM交BD点F。

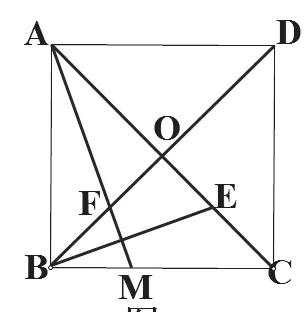
图1

（1）求证：OE=OF。

（2）如图2，若点E在AC的延长线上，AM⊥BE于点M，交DB的延长线于点F，其他条件不变，则结论“OE=OF”还成立吗？如果成立，请给出证明；如果不成立，请说明理由。

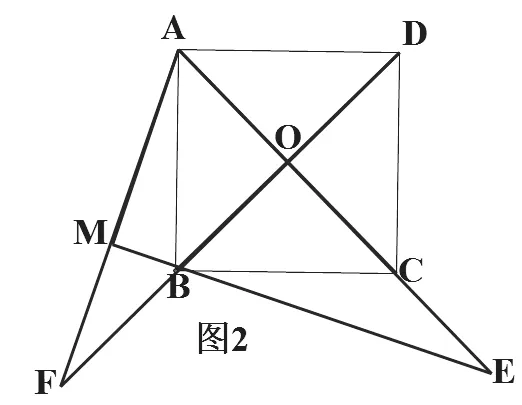
图2

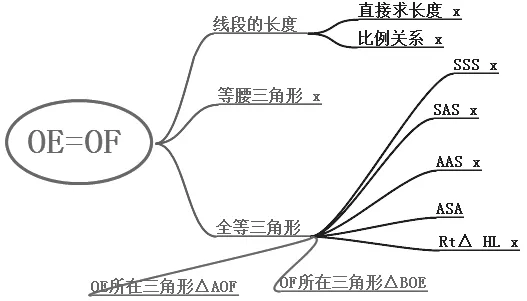
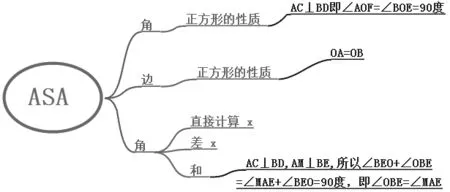
以这题为例，要求证OE=OF，而证明OE=OF，可以有三种方法，分别是求线段的长度、等腰三角形两腰相等、全等三角形对应边相等。求线段的长度可以有两种方式一是直接求长度，从题目的条件不能直接求出，所以排除，导图中用打“×”表示排除此方法，二是比例关系求长度。但是根据已知条件，也是不够条件用比例关系求长度，也排除。等腰三角形需要在同一个三角形中，所以需要构造辅助线，再利用等角方法证明其为等腰三角形，把问题复杂化。全等三角形证明线段相等，是经常使用的方法，所以可以再继续探究，再从已知条件入手，进入分析，发现全等三角形的方式合适简单，从而选择全等三角形方法求证线段相等。在分析的时候可以利用思维导图把三种方法进行分析，排除，最终选择合适的方法。如下图所示。通过这一步一步的分析，学生既明确这题的解题方法，同时又掌握求证线段长度相等的三种方法，以后遇到这样求证边长度相等的方法，也可以通过这样的分析，选取自己合适的方法证明，从而掌握数学解题的方法，提高学生的分析能力，让自己在以后的习题中通过自己的演绎分析获得解题思路。

思维导图是学习数学的工具，它帮助学生预习、复习和分析题目。发散思维导图在数学问题分析中的应用能够提升逻辑思维能力，锻炼数学的思维能力。

[1]托尼·巴赞.李新译.思维导图[M].北京:作家出版社，1999.

[2]中华人民共和国教育部.全日制义务教育数学课程标准(2011年版)[S].北京:人民教育出版社，2011.

[3]中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.