有机融入出奇效 合作研讨成典范
——“大数的认识”课例生成记
□冯 晶
一、引言
近些年来,随着HPM(History and Pedagogy of Mathematics,数学史与数学教学)领域研究的不断深入与HPM教育价值研究的相对成熟[1],HPM研究逐渐向教学实践延拓,中小学数学教师也试图将数学史应用于课堂教学,但受困于数学史料的匮乏、数学史融入课堂教学经验与相应评价体系的缺失等[2],数学教师并没有开发出数量可观的优秀HPM课例,特别是小学阶段,好的HPM课例更是凤毛麟角。就当下现实而言,开发出一节精彩的HPM的课例显得尤为重要。好的课例可以为一线教师学习和逐步掌握数学史融入数学教学的策略提供范例作用。本文将以沪教版四年级上册“大数的认识”为例,来研磨小学HPM的实施策略,以期对小学数学教师掌握策略提供启示,同时,本研究也力图将此课例打造成HPM的经典课例,以为更多的同行研究之用。
二、教学磨课与课例生成过程
(一)教学磨课与课例形成的大致过程
按照教学进度,在“大数的认识”授课前两周,授课教师F与W团队(W是国内知名的HPM专家,团队中负责小学阶段的是Y)取得了联系,双方就教师F的第一次教学设计进行了研讨;研讨后教师F进行了第二次教学设计,并与Y讨论后对教学设计进行了修改;借助已修改的教学设计,教师F进行了磨课,W团队中的部分成员参与磨课,课后对教学设计提出了新的改进建议,同时,W与参与磨课的成员就课例作了进一步研讨;教师F根据Y提供的反馈,进行了再设计,并与Y讨论后作了调整;教师F依据调整后的教学设计进行授课,W团队参与了听课活动,并与教师F就教学情况进行了讨论。
(二)教学内容的具体变化及背后的原因
尽管在课例的开发过程中,教师F进行了7次教学设计及修改,但按照图1显示的过程,主要的设计有3个,第一次教学设计(以下简称OD),它代表了W团队参与前,教师F的原始想法,磨课时用的教学设计(以下简称TD),正式上课时用的教学设计(以下简称FD)。
(1)从OD到TD
在OD中,教师F欲从学生是否知道阿基米德来引入数沙的故事,“他就是阿基米德,出生在希腊西西里岛叙拉古附近的一个小村庄,是一位贵族,与叙拉古国的赫农王有亲戚关系,家庭十分富有。国王的儿子盖伦和阿基米德是好朋友,这位盖伦王子不相信有人能数出沙子的数量,并曾和阿基米德谈论过此事。后来阿基米德就写了《数沙者》的书献给王子。阿基米德认为不仅西西里岛沙滩上的沙子可以数出来,就连全世界的沙子也能数出来”,并通过“你心中的大数是什么样的?”“你现在所知最大的数够不够用?”两个问题引发学生的兴趣与思考,鼓励他们表达心中的想法。随后的设计按照教科书思路将大数的认识与中国(包括各省、市、自治区、特别行政区)的人口联系起来进行学习,不再有数学史内容的出现。
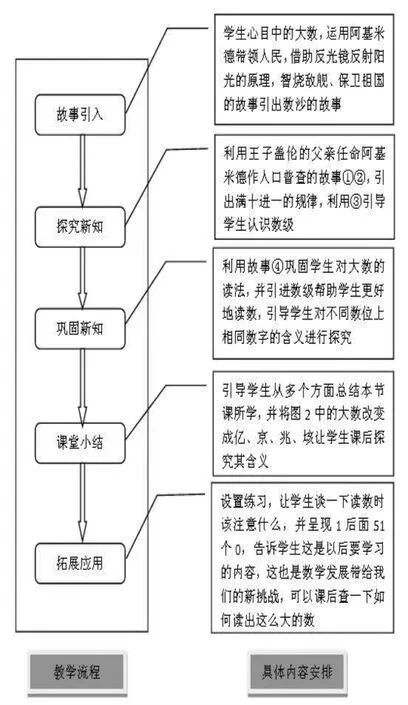
图1 FD的教学流程与具体内容安排
在针对OD的研讨中,W团队的成员认为F使用数学史的方式比较粗浅,仅利用附加式在引入部分加入了一点数学史来激发学生学习兴趣,而且故事中对阿基米德出身的介绍与教学内容匹配度较低,去掉这部分设计对学生知识理解无影响,教师F也认同这一点,而要发挥出数学史的作用,可以用阿基米德的故事串联整个教学活动。因此在TD中,教师F首先设计了问题“你心目中的大数是什么样的,比如?”“你所知道最大的数够用吗?”来引出主题,然后进一步设计了问题“你觉得有没有人能数出宇宙中的沙粒数量”,从而引出阿基米德数沙的故事“(出示阿基米德像)小朋友,你知道他是谁吗?他是阿基米德,公元前287年出生在西西里岛叙拉古附近的一个小村庄”,播放音频,“《数沙者》这本书是阿基米德写给好朋友盖伦王子的,因为那个时代,有些人认为宇宙中沙子的数量是无限的。另外一些人,虽然并不认为沙子的数量是无限的,但是,他们不能写出一个足够大的数,使它在数量上超过宇宙里全部沙子的数量。于是,通过阅读前人的著作,做了一系列准备工作后,阿基米德创造出了一套完整的计数理论,并表达出了‘宇宙’所包含的沙粒数小于1后面51个零”,随后创设了阿基米德“人口统计”故事的情境。
①作为王子,盖伦想要了解欧洲的人口数量。但他事务繁忙,所以委派连宇宙的沙子都能数出的阿基米德负责这件事。阿基米德从故乡叙拉古着手这一工作,岛上现在有9999(九千九百九十九)人,这一天,岛上的一位妇人生下一个婴儿,请问现在这个岛上的总人数是多少?
②阿基米德派出去做人口调查的10个官员已有9人回来,人口总计90000(九万)人,还有一个前去较远的地方的官员尚未返回,阿基米德在着急地等待中。傍晚时分,最后一人姗姗来迟,带回的数字是10000(一万)人。假如你是阿基米德,你会向盖伦王子汇报多少人?
借此引导学生认识数位表,并认识相邻计数单位间的进率是十,满十进一;随后,通过“这位伟大的数学家死于公元前212年叙拉古战役中,在他生活的那个年代,全世界的人口不过五百万,如果阿基米德还活着,一定会感叹:中国真是一个大国啊!单我们上海在2010年第六次全国人口普查中就有那么多(23019148)人”,借此帮助学生认识级数,学会读数,通过问题“我们中国究竟是一个怎样的大国呢?如果阿基米德知道了中国的人口数,我想他一定很惊讶,到底是多大的人口数呢?”帮助学生巩固新知,理解不同数位上的相同数字表示的含义不同。在课堂小结环节,除了知识的总结外,F还总结道:“今天,记录大数看起来是非常微不足道的事情,在阿基米德时代,能找到一种记录大数的方法的确是一个伟大发现。其实这也是数学这门科学向前迈出的重要一步。在我国古代也有比较完整的大数进制(如图2)。无论是古希腊还是我国古代先人都有对大数的表达,正因为有了他们的贡献,我们的物理学、天文学等学科才能得以顺利发展。”最后,在拓展应用部分,除了提供相应的题目外,还呼应第一部分,设计了问题“你能读出阿基米德数出的沙粒数吗?即1后面51个零”,试图为科学计数法做铺垫。

图2 中国古代的大数单位
(2)最终教学设计的形成
在磨课后的研讨中,参与者结合课上出现的一些问题,提出了既然语文课中已经有了阿基米德的故事,不妨在介绍他时,从语文教材中的片段入手,将数学与语文结合起来,让学生感受文化的魅力;即使告诉学生宇宙中所含的沙粒小于1后面51个零,学生也没有什么概念,所以干脆将TD中的“并表达出了‘宇宙’所包含的沙粒数小于1后面51个零”改成“当时由于没有先进的计数单位,稍微大的数古人很难读出来。但是数学发展到了今天,我们有了先进的计数单位,我们有能力读出一些较大的数,今天我们就来学习这些内容”,一方面激发学生的求知欲,给学生一种随着时代的进步,数学也在不断发展的印象,另一方面以“但是由于没有先进的计数单位,稍微大的数古人很难读出来”为后面的故事串联埋好伏笔;图2中呈现的中国古代的大数单位太多,学生理解不了,1后面的51个0,尽管教师F说了读作“10的51次方”,但学生也理解不了,而且这些内容不是本节课所要求理解的,把这些内容放进来的目的是让学生感受中国古代的数学成就,激发他们探究未知的兴趣,因此可以作为课后活动供学有余力的学生探究;学生在读数时存在一定的困难,应该通过分级的探究活动帮助他们克服这一难点。在W团队的研讨过程中,W认为这节课的故事串联不够自然,特别是如果阿基米德还活着这一假设十分突兀,所以建议运用古今对照的方式。
③很久以前,做人口普查需要像阿基米德这样的大数学家,而且虽然他们能用一些方式表示欧洲人口的数目,但是却读不出这些数字,而今天的我们不一样,即使是像你们一样的小朋友也能读出很大很大的数,比如上海在2010年第六次全国人口普查中就有那么多(23019148)人。(认识数级环节)
④在阿基米德生活的年代,全世界的人口不过五百万,如果阿基米德要读出中国的人口数,我想他先昏过去再说。但我想小朋友们肯定能读出来,不信你们读一下?(巩固新知环节)在使故事顺畅自然的同时,激发学生学习数学的自信心。
在课堂小结环节,将图2改为了“在我国古代也有比较完整的大数进制,如亿往后的京、兆、垓等。小朋友们可以在课后查一下这些词的具体含义”,并将其后“数学对物理学、天文学等学科的推动作用”改为“社会、数学、物理学与天文学等之间的相互推动作用”,增加了“事实上,无论是古希腊还是我国古代先人对大数都有自己的表达形式,但是古人不一定有先进的计数方法并能够顺利地读出这些大数。正因为社会的需要,数学才能不断发展,我们才能读出物理学、天文学等学科的大数据”。
最终,教师F设计了如图1的教学流程进行正式的授课。
三、反思与结论
通过三次研讨、两次主要的教学设计改动、一次磨课,通过从选取素材到教师反思等多个环节的螺旋推进,教师F最终的授课取得了相当不错的效果。但通过上述的分析发现,HPM课例的生成并不是一件容易的事情:一方面,需要多方人员的积极参与和配合,除了W的团队外,教师F所在学校的学科组也从知识掌握的角度给予了帮助;另一方面,任何设计上的改动都要有所依据,比如从故事的完整性上看,与OD相比,TD增加了阿基米德作为人口普查员的故事,阿基米德来到今天的故事,但考虑到故事串联的自然性,与TD相比,FD遵照史实将阿基米德来到今天改成了尽管他能表示出很大的数,但是他也读不出这些数,而今天连小朋友都能读出很大的数,起到了激发学生积极性与提升信心的目的,比如从具体细节来看,无论是在故事引入环节还是在拓展应用环节读出1后面51个0都是不可取的,所以干脆在引入中不出现1后面51个0,只是在拓展应用环节点出这是以后要学习的内容,这也是数学发展带给我们的挑战,为后续的学习做好铺垫,将图2改成亿、京、兆、垓等的查阅也是考虑到学生的认知基础,同时让学生感受不同的数学文化。但数学史在学生身上体现出的知识之谐、方法之美、探究之乐、能力之助、文化之魅、德育之效等教育价值又指引着我们积极尝试融入数学史的设计。因此,正如“大数的认识”课例的生成过程一样,在课例开发的过程中,我们应该加强高校研究团队与一线教师团队的沟通、合作,通过研讨来加强教育取向的数学史研究的深度,通过磨课来试验与加强数学史与教学内容的契合程度。

参考文献:
[1]吴骏,汪晓勤.国外数学史融入数学教学研究综述[J].比较教育研究,2013,(8):78-82.
[2]Fauvel,J.,&Van Maanen,J.History in Math⁃ematics Education-the ICMI Study.Dordrecht,Kluw⁃er Academic Publishers[M],2000:203.

