国际视野下小学HPM课例评析
□王 鑫 沈中宇
一、引言
早在19世纪,数学史与数学教育之间的关系就受到欧美数学家和数学史家的关注。1972年,在第二届国际数学教育大会上,成立了专门的数学史与数学教育关系国际研究小组(International Study Group on the Relations between History and Pedagogy of Mathematics,简称HPM),标志着数学史与数学教育(也简称为HPM)成为数学教育学科中重要的研究领域之一。而在国内,直到21世纪初,HPM才开始受到学术界的普遍关注,近年来HPM在国内取得了长足的发展,教育取向的数学史研究逐渐深入,数学史融入数学教学的实践与日俱增[1]。国内小学阶段的HPM研究虽起步较晚,但已涌现了一批精彩的HPM课例,受到越来越多研究者与教师的关注。
鉴于国际上HPM研究早有传统,学习和分析国际HPM研究有助于促进我国数学史与数学教育的研究,然而已有研究表明,国内数学史与数学教育研究缺乏对国际上该领域研究动态及成果的关注[2],目前国内也鲜有对国际上小学HPM领域教学实践的相关介绍。因此,我们将从国际的视野出发,采撷国际上典型的HPM课例进行介绍,从中归纳出这些课例的特点,给今后的HPM实践带来借鉴和启示。
二、课例选取
在希腊的数学课程中,数学史是重要的组成部分,早在20世纪末期,其教材的每一章中都渗透了数学史,且教师必须在课堂中使用[3],在《学校中的数学》和《科学与教育》等国际数学教育杂志中也时常可见来自希腊的HPM研究。在中国台湾地区,台湾师范大学数学系洪万生教授及其研究团队多年来一直致力于HPM的研究与实践,他们创办的《HPM通讯》已有十余载,其成果对海峡两岸数学教育界都产生了深远影响[4]。
因此,我们选取了来自希腊和中国台湾地区的4个HPM课例[5-8],其中2个涉及一笔画问题,1个涉及分数乘、除法,1个涉及圆周率π,期望通过对这些课例的分析,了解国际视野下小学HPM研究的动态,从中汲取经验。
三、课例分析
(一)穿越哥尼斯堡桥
“穿越哥尼斯堡桥”是2003年在希腊塞萨洛尼基实施的一则HPM课例,授课对象为11岁左右的六年级学生。整节课围绕以下情境:很多年前,瑞士的大数学家欧拉(Leonhard Euler,1707-1783)到德国哥尼斯堡访问,偶遇了一群好奇的散步者,他们向欧拉提出心中困惑已久的疑问:能否找到这样的一条路线,使得从哥尼斯堡的任何地方出发,不重不漏地穿过所有七座桥(图1)?
教师先给学生讲述了这个著名的七桥问题,画出示意图(图2),然后抛出问题1供学生探究:起点的选取对找到符合要求的路线有影响吗?学生的尝试均以失败告终,由此得出结论:无论起点在哪,都无法找到符合要求的路线,并猜测这一事实可能与桥的数量有关。于是,教师提出问题2:桥的数量是导致无法找到路线的原因吗?如果少一座桥或多一座桥,那么有可能找到不重不漏一次走完的路线吗?教师分别将六座桥与八座桥的不同分布图随机分发给学生,学生很快便找出符合要求的路线,经过分享交流,发现每种分布图中符合要求的路线可能还不止一条,但起点与终点始终都是其中特定的某两个点。进一步,教师又提出问题3:路线存在与否真的是取决于桥的总数吗?还是说,取决于桥的分布即连接四个地区之间桥的特定数量呢?三个问题环环相扣,层层深入,最终答案通向一笔画问题的本质,只有以下两种情形才能找到符合要求的路线:(a)每一地区都有偶数座桥与之相连;(b)有且仅有起点和终点两个地区有奇数座桥与之相连,其余地区都有偶数座桥与之相连。

图1 哥尼斯堡七桥问题
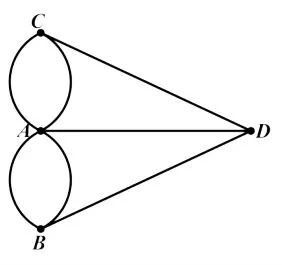
图2 七桥问题示意图
(二)阿基米德与π
“阿基米德与π”是2013年在希腊实施的HPM课例,授课对象为27名六年级学生。教科书上介绍了半径为α的圆的面积大约是以圆的半径为边长的正方形面积的3.14倍(图3),那么,为什么π大约是3.14而不是其他的数,比如3.13或3.15呢?为了回答学生的这一疑问,教师基于古希腊数学家阿基米德(Archimedes,287B.C.-212B.C.)的方法设计了本节课。
首先,教师提出问题1:为了找出图3中的圆面积是正方形面积的多少倍,我们需要知道哪些条件?问题2:你们认为用圆内接等边三角形的面积来近似替代圆的面积是一个好办法吗?圆外切等边三角形呢?问题3:如果第一个三角形(指圆内接等边三角形)的面积比圆面积小,第二个三角形(指圆外切等边三角形)的面积比圆面积大,那么你对圆的面积有何看法?由此学生产生了一种上限与下限夹逼的思想,从而想到用它们的平均数来近似替代圆的面积,只需比较圆的近似面积与正方形面积就可以求出π的近似值。借助Cabri软件的测量面积功能,学生算出面积之比为3.247551,与3.14还有一定出入,于是教师又提出问题4:显然你们对我给出的三角形并不满意,关于如何进行下去你们有什么好的建议吗?受此启发,学生产生了与伟大的数学家阿基米德同样的想法,即增加内接与外切多边形的边数。利用软件作图、测量,学生依次计算出正六边形对应的面积之比为3.031122(图4),正十二边形对应的面积之比为3.107653,正二十四边形对应的面积之比为3.132755,正四十八边形对应的面积之比为3.1393,这是一个比较令人满意的π的近似值了。进一步,教师又让学生挑战圆内接与外切九十六边形。最后通过问题5:难道你们不认为继续增加多边形的边数直到将圆完全覆盖是一个好主意吗?给学生渗透了极限的思想。
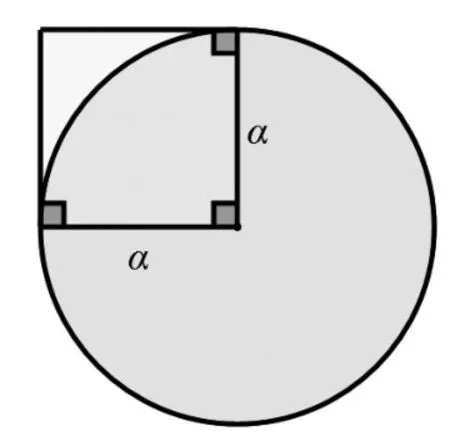
图3 圆和以圆的半径为边长的正方形

图4 圆内接与外切多边形
(三)魔术桥
“魔术桥”是2009年在中国台湾地区实施的一系列数学史融入数学教学模块课程,由三节内容相关的课构成,在五年级和六年级的两个班级分别实施了实验教学。围绕数学家欧拉及七桥问题等相关数学史,教师设计了十张学习单(图5),包含四大主题:认识欧拉、一笔神功、数独和魔方阵。第一节课介绍了一笔画问题,首先,教师播放Flash动画来描述七桥问题,引导学生结合学习单上的图解讨论欧拉是如何解决这个问题的,引出一笔画问题。然后,通过练习简单图形引导学生归纳一笔画问题的原理,并给学生提供自由设计图形的空间。最后,以拉丁方块(一种n×n的方阵,恰有n种不同的元素,每一种元素在同一行或同一列里只出现一次)为重点讲解欧拉的其他发明故事,为第二节课做铺垫。

图5 学习单“认识欧拉”
第二节课教师便介绍了改编自拉丁方块的数独(一种9×9的方阵,根据已知数字推理出所有剩余空格的数字,并满足每一行、每一列、每一个粗线宫3×3内的数字均含1~9,不重复,又称九宫格),讲解过程中融入了数独的历史。紧接着,第三节课的学习内容是相似概念的魔方阵(一种n×n的方阵,组成元素为自然数1、2、…n,满足每行、每列及主、副对角线上各n个元素之和都相等,又称幻方或纵横图),其间也穿插了魔方阵的历史。这三节课的每一主题难度由浅入深,可分开进行独立教学,整合起来又构成一个完整的单元。
(四)分数乘、除法
“分数乘、除法”是2009年在中国台湾地区实施的单元教学实验,对象为小学六年级学生,教师设计了八张相关的数学史学习单。首先,围绕“约分”这一分数乘法的基本活动,教师介绍了我国《九章算术》中的“更相减损法”以及为其作注解的数学家刘徽(公元3世纪),还有西方的“辗转相除法”,并介绍了古希腊数学家欧几里得(Euclid,330B.C.-275B.C.)和《几何原本》(图6)。然后,教师带领学生复习了五年级所学的分数加、减法,并引入《九章算术》中的合分术(分数的加法)与减分术(分数的减法),结合方田章中的题目,让学生比较古今算法的异同。接着,利用方田章中已知长方形土地的长与宽,求面积的题目和分财产的问题分别介绍了《九章算术》中的乘分术(分数的乘法)与经分术(分数的除法),古今对照,揭示法则的含义。

图6 学习单“更相减损法”与“辗转相除法”
四、国际视野下小学HPM实践的特点
通过对上述课例的分析,我们可以归纳出国际上小学HPM实践具有以下特点。
(一)数学问题环环相扣,信息技术凸显高效
数学史是一个巨大而丰富的宝藏,历史上的数学问题可以为今天的课堂教学提供借鉴。“基于数学史的数学问题串”是以相关数学史料为主线,紧扣数学教学目标,运用一定策略提出的一系列具有内在联系、构成一个整体的数学问题。问题串的设计与使用为学生提供了“再创造”的机会,有助于学生在探究中经历数学知识发生、发展的过程,积累数学活动经验,感受“探究之乐”,体会数学的本质,同时也有助于增强数学教学的层次性、连贯性和整体性。在“穿越哥尼斯堡桥”与“阿基米德与π”两个课例中,均涉及基于数学史提出的问题串。前者的问题串如图7所示,三个问题使学生的关注点从起点的选取到桥的总数,再到四个地区之间桥的数量分布,大胆猜想,小心验证,一步步揭示出一笔画问题的本质。后者的问题串如图8所示,经过前四个问题的启发,学生自然而然产生了倍增多边形边数的想法,与阿基米德的方法不谋而合。

图7 “穿越哥尼斯堡桥”问题串

图8 “阿基米德与π”问题串
随着现代信息技术的飞速发展,信息技术在数学课堂中发挥着愈来愈积极的作用,其优点至少体现在以下三个方面:(1)利用信息技术可以克服传统教学所面临的困难,创设良好的教学环境,把学生看不见、摸不着的数学生动直观地呈现出来,激发学生学习数学的兴趣,促进理解;(2)变学数学为“做”数学,使学生有机会像数学家一样去实践操作、发现真理,发现数学的奥秘,收获成功的喜悦;(3)信息技术的运用可以降低问题解决的难度,符合学生的认知基础。在“阿基米德与π”一课中,教师借助信息技术的力量克服了一系列的困难和障碍,让每一名学生都有机会成为小小数学家,把常规课堂上靠黑板和粉笔难以实现的操作变为现实,从正三角形到正六边形、正十二边形……最后到正九十六边形,一步步追寻阿基米德的脚步揭开π的神秘面纱。在这个过程中,信息技术把古代数学家的精彩思想与巧妙方法活灵活现地再现于今日的课堂上,赋予了数学史二次生命,让数学教学更加高效。
(二)单元模块教学一线贯穿,数学史学习单沟通古今
单元模块教学是把教科书中具有内在联系和共同主题的数学知识串联成一个整体进行讲授,有利于学生习得系统的知识,知晓前后知识之间的联系。台湾的数学教育研究者采用模块教学,开发出配套的“数学史学习工作单”(简称学习单)。学习单是教师根据教学目标和教学主题,基于数学史而设计,由教师提供给学生,帮助学生完成学习任务的一种学习、教学和评量工具[9]。学习单可以培养学生自主探究、合作交流的能力,拉近学生与数学、历史与现实之间的距离,帮助学生更好地建构对知识意义的理解,体验“探究之乐”“文化之魅”等多种价值。也就是说,教师可以采用附加、复制、顺应、重构[10]等多种方式将史学形态的数学史料转化成教育形态的教学材料,融入到学习单中,进而融入数学教学。以上课例为我们做出了很好的示范。
模块课程“魔术桥”的一系列学习单形象生动,图文并茂,用小故事和漫画的形式讲述七桥问题,并从七桥问题衍生出一笔画问题、拉丁方块问题等,利用数学史串联了数学知识。“分数乘、除法”学习单既涉及东方著作《九章算术》“更相减损法”的古今对照,又有西方经典《几何原本》中的“辗转相除法”与之遥相呼应,利用基于数学史设计的学习单让学生体会到了探究的乐趣,并让刘徽与欧几里得两位大数学家穿越时空进行“对话”,体现了数学的多元文化。
五、启示与展望
放眼国际视野下小学HPM课堂,我们看到数学史的种子已经深深种在了各国数学教育研究者的心中。小学阶段是实施数学史融入数学教学的一片亟待开发的沃土,在今后的HPM实践中,我们可以尝试从以下一些方面进行改进:对于概念课的教学,教师应该思考如何顺应历史上数学概念的产生、发展来设计问题串,为学生搭建脚手架,引导学生进行探究;小学生的思维一般离不开具体事物的支持,因此教师要充分利用信息技术这个数与形之间的媒介,再现数学家的经典思想方法,让数学在课堂上“动”起来,激发学生的创新思维,培养直观想象素养;此外,数学史融入小学课堂也不仅仅局限于单个课例的开发,今后可以更多地尝试进行模块教学,寻找合适史料设计学习单开展教学,从而调动学生的学习主动性,渗透多元文化,让数学史在数学教学中的融入发挥更大的教育价值。
以上介绍的课例中出现的《九章算术》与刘徽等史料也提醒我们,曾几何时,中国的数学水平世界领先,我们在学习和借鉴国外数学教育先进经验的同时,还要充分挖掘和利用自己本国的数学史资源和数学教学资源,将中国博大精深的数学文化,具有中国特色的数学教育传播到世界各地。
参考文献:
[1]汪晓勤.HPM:数学史与数学教育[M].北京:科学出版社,2017.
[2]康世刚,胡桂花.对我国“数学史与中小学数学教育”研究的现状分析与思考[J].数学教育学报,2009,18(05):65-68.
[3]Fauvel,J.&Van Maanen,J.History in Mathe⁃matics Education[M].Springer Netherlands,2015.
[4]黄友初.一线教师对数学史认识的误区与改善——基于两岸比较的视角[J].教育研究与评论(中学教育教学),2016,(10):41-45.
[5]Chassapis,D.&Kotsakosta,M.Crossing the Bridges of Königsberg in a Primary Mathematics Classroom[J].Mathematics in School,2003,32(1):11-13.
[6]陈玉明.数学史融入教学实践之分析——以“魔术桥”为例[J].台湾数学教师电子期刊,2009,(18):18-31.
[7]蔡幸霓,苏意雯.数学史融入国小数学教学之实作研究——以分数乘、除法为例[J].台湾数学教师电子期刊,2009,(20):17-40.
[8]Papadopoulos,I.(2014;2013;).How archime⁃des helped students to unravel the mystery of the mag⁃ical number pi[J].Science&Education,2014,23,(1):61-77.
[9]代乐乐.探究型学习单在小学数学课堂中的运用[J].基础教育研究,2017,(15):60-62.
[10]汪晓勤.HPM视角下的小学数学教学[J].小学数学教师,2017,(Z1):77-83+2.

