改进创新的坐标系证明哥德巴赫猜想之再研究

山西省阳泉市晋东化工厂 赵发耀长春师范大学 王一洲

一、证明“猜想”的思路

“猜想”可用y=a+b表示，式中y为大于4的偶数，a和b均为质数。该式为有约定条件的含有两个未知数的二元一次方程，隶属于数论研究的范畴，采用常规的方法是很难证明的，因此公认为数学难题之一。

业内专家断言，现有的数学工具是无法证明“猜想”的【注】，其用意是告诫数学爱好者不要进行无效的劳动，但并未否定使用改进后的数学工具是可以证明“猜想”的观点（包括“猜想”正确或错误）。

鉴于上述原因，原文采用了改进创新的二维坐标系，即只取直角坐标系的第一、第二象限并规定：x轴只标注第一象限从0开始的自然数；y轴只标注从6开始的偶数，然后以y轴每个y值为中点，作平行于x轴的平行“线段”，“线段”长度与每个y值相匹配，这样构成了图形的整体结构（以上y、x和线段，三者同比例）。

需指出，“线段”具有三种功能：第一，每条线段上，所有点位的数值都等于线段中点之y值；第二，线段上存在着两组相反方向的含0自然数；第三，质数a的表达方式是，从线段左至右逐渐增大。质数b则相反，从右至左逐渐增大。

该坐标系可使y、x、a、b和n形成相关关系图形（原文图①缺省，图②复制于下面，n值含义见下节）。

二、建立证明“猜想”的公式（方程组）

1.建立6～100偶数与构成其全部两质数组合公式

简要回顾原文分析和总结6～100的偶数与构成其全部两质数之间规律的过程：

从图②中确认，任何质数a可表示为a=y-3,即y=a+3,又可表示为y=（y-3）+3。

但比如偶数12，不能用12=9+3表示（9非质数），用12=7+5则可；再如30=27+3=25+5也非两质数组合，而30=23+7=19+11=17+13则可（30=21+9也非两质数组合）。总之，6～100内的许多偶数具有同样的规律。

这种规律可用下面的方法表示：在[（y-3）+3]式中，前项减2n，后项加2n，则可形成只含奇数的组合，然后再从中求得两质数的组合。即：

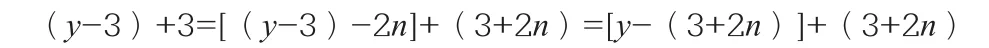
整理上式可得公式（方程组）：

（大写A、B表示奇数，小写a、b表示为质数）

图形已经确定了方程组中各参数的取值范围是：

Y为6～100的偶数。

A为≤A≤y-3内的奇数；a为≤a≤y-3内的质数。

B为3≤B≤内的奇数，且A≥B；b为3≤b≤内的质数，且 a≥b。

n为从0～（-3）/2范围内不能被3整除（因系3的约数，故舍去）的含0自然数（n取值范围说明：方程组（1）式减（2）式，整理后得：式中当A取最大值A=y-3，B取最小值B=3，可得到n=0；当A取最小值A=，B取最大值B=，可得到

上述取值的范围内，A、B、a、b以及n全部吻合。

在上面的方程组中，由式（3+2n）筛选去了全部偶数加偶数等于y的组合，占到y值的数量；因A和B仅取图②右侧只含奇数的组合，又筛选去全部两奇数组合的；再由n值中有“不取能被3整除”的自然数规定，又筛选去约的两奇数组合。

经验证，在6～100偶数中，按照取值范围规定的n值之中，存在着既能使式（3+2n）得到质数b，又能使式[y-（3+2n）]得到质数a的“正确的n值”。它（们）使每个偶数求得了全部两质数组合，与原样数据完全吻合。

按照上述y、a、b和n的取值范围规定，经多次验证确认，目前最大质数表中所涵盖的大于4的偶数，均可由取值“正确的n值”中，求得全部两质数组合。

说明：原采用6～100的偶数与组成其全部两质数组合为样本，因图形视觉效果差，改为了6～34的偶数，即图②。

2.探究6～∞偶数与其全部两质数组合公式

上述方程组的结构，举一通俗例子加以解释：比如一条标准有100单位的软尺，分别取第6,8,10……直至100单位，再分别从中间对折，形成了上下两条软尺，其中一条视为方程组（1）式，另一条为（2）式，然后在上、下对齐的软尺中，只分析不能被3整除的奇数对应奇数的组合，从某些共同点位（即2n）可求得各个偶数段的全部两质数组合。

如果无限延长“软尺”直至无穷大偶数，再进行对折，以求得大于4的偶数之全部两质数组合，那么形成的公式与上述方程组是相同的。

由于质数无限多，n取值数量也随之增多，其结果是，每个大于4的偶数从取值“正确的n值”（至少有一个n值）中，可求得全部两质数组合，亦即证明了“猜想”是成立的。

综上所述，本方程组证明“猜想”的关键是取值“正确的n值”。

三、论证取值正确的n值与两质数a+b的关系

前提条件：方程组（1）式+（2）式得：y=A+B（式中各参数取值范围同前）。

方程组（1）式-（2）式得：y-2（3+2n）=A-B，整理后得：

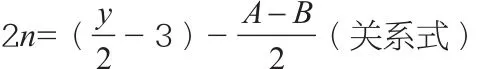
式中的（-3），在图形中是A取最大值、B取最小值的位置，也是图中x 的最大值位置；表示奇数A+B 结合点在图中位置（式可理解为从A的长度左边起，减去B的长度之差的一半的位置，该位置位于y轴右侧且等于此点位的x值，即此点位也是A+B=y和2n的位置）。

例如:y=12时，n取值为0和1；（A取值为9和7，B取值为3和5），将n值0和1代入关系式得：

式中A和B的位置只能填入7和5，别无它选。

通过上例证明了n的作用是使方程中A和B有解，A和B是否是两质数a+b，从上面关系式可知，只要n值正确，那么，2n代入公式中，可得到两质数a+b组合，反之亦然，即2n与两质数a+b互为充要条件，也是6～∞偶数的共同规律。

同时也确认了取值“正确的n值”表达式为：/2，该式不及表达得准确。

四、推导证明“猜想”的最终公式（设n为取值正确的n值）

方程组（1）式-（2）式整理后得：

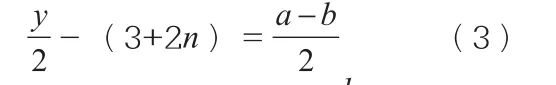
前面已分析过，式所以有：

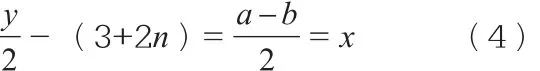
由（3）式与（2）式得：即：

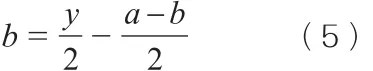
再由（1）式，（2）式和（5）式得：

综合（4）式，（5）式和（6）式，并与图②同一位置的x值相结合，得到证明“猜想”的最终公式为：

即证明了“猜想”是成立的。

式中x的取值范围为：0≤x≤y-3内的含0自然数（图形已确定）。

本文用建立数学模型的步骤，推导出证明“猜想”的公式（方程组），经论证导出了对6～∞的偶数均适用的结论。其共同规律是：在这些偶数规定范围内的n值之中，至少有一个“正确的n值”，于是得到了与“2n”互为充要条件的两质数a+b组合，使“猜想”得到证明。

在图形中，正确的2n与两质数a+b=y的组合以及值，三者相互重合，由此推导出证明“猜想”成立的最终表达式【见文中第（7）式】。