考虑中间主应力效应的筒仓侧压力计算
孙珊珊,赵均海,张常光
(长安大学 建筑工程学院,陕西 西安 710061)
0引 言
筒仓仓料产生的仓壁侧压力是作用在筒仓结构上的主要荷载,侧压力计算的正确与否是筒仓合理设计的基础,是确保工程安全和经济性的前提[1-6]。
对于深仓,各国规范均以Janssen公式为基础[7],但所采用的侧压力系数计算方法有很大不同,常用的侧压力系数有Rankine主动土压力系数、静止土压力系数或修正静止土压力系数,以及考虑仓壁摩擦由平衡条件求得的侧压力系数等[7]。
对于浅仓,各国规范对仓壁侧压力的计算方法各有不同,经典的浅仓侧压力计算理论主要有[7]Rankine理论、修正Coulomb理论,二者均基于Mohr-Coulomb(M-C)准则,并未考虑中间主应力的影响。Rankine理论建立在无限长挡土墙的基础上,不考虑浅仓的边界条件,并且忽略了仓料与仓壁间的摩擦力;修正Coulomb理论考虑了仓料与仓壁的摩擦力及仓料内所形成的楔体,且假定滑动面是平面。二者计算的侧压力均与仓料顶面或仓料锥体重心到计算截面的距离呈线性增大关系,差异在于侧压力系数的不同,Rankine理论中侧压力系数为主动土压力系数,而修正Coulomb理论采用的侧压力系数与仓料内摩擦角以及仓壁外摩擦角相关。
实际上,筒仓内的仓料处于三向不等应力作用的平面应变状态,仓料强度受中间主应力的影响显著,不考虑中间主应力影响的M-C准侧不能真实反映仓料的强度潜能,得到的仓壁侧压力偏于保守,选择一个合理又恰当的真三轴强度准则,例如Drucker-Prager(D-P)准则、Matsuoka-Nakai(M-N)准则、Lade-Duncan(L-D)准则和统一强度理论(UST),不仅可以提高工程的质量和耐久性,而且还能带来巨大的经济效益和社会效益。
因此,本文基于D-P准则、M-N准则、L-D准则以及UST理论,分别推导了平面应变状态下4种考虑中间主应力影响的侧压力系数表达式,并给出了相应的适用条件,进而将其应用于深仓和浅仓的侧压力计算,并与试验数据和多国规范值进行了比较和验证,所得结果可为筒仓优化设计提供一定的理论指导和建议。
1筒仓侧压力原理及基本假定
1.1筒仓侧压力原理
筒仓侧压力示意如图1所示。对于深仓,仓壁水平侧压力Ph的计算公式为
Ph=Chγρ(1-e-μks/ρ)/μ
(1)
式中:Ch为修正系数,与计算高度有关,按照《钢筋混凝土筒仓设计规范》[8]取值;γ为仓料重度;ρ为筒仓水平净截面的水力半径;μ为仓料与仓壁的摩擦因数;k为侧压力系数;s为仓料顶面或仓料锥体重心到计算截面的距离。
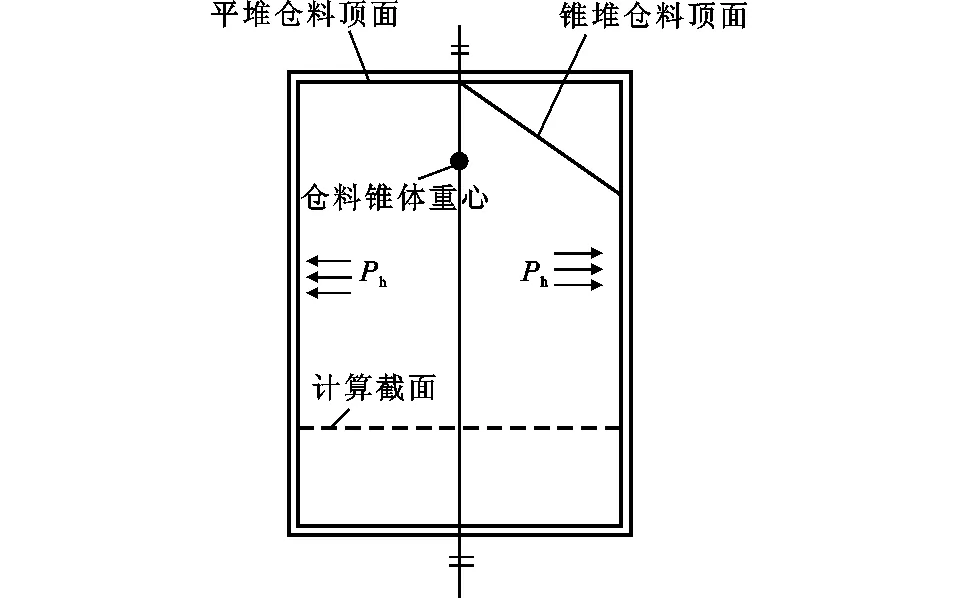

对于浅仓,仓壁水平侧压力Ph的计算公式为
Ph=kγs
(2)
当采用Rankine理论时,侧压力系数k为
(3)
采用修正Coulomb理论时,侧压力系数k为
(4)
式中:φ为仓料的内摩擦角;φ′为仓壁的外摩擦角。
可见,不管是深仓还是浅仓,侧压力计算的关键均是侧压力系数k的合理确定。同时,仓料属于颗粒状的岩土类材料,可类比挡土墙问题确定砂性土产生的侧向土压力方法,来求解平面应变状态下的侧压力系数k。
1.2基本假定
(1)将筒仓侧压力计算视为平面应变问题[9-10],并且中间主应力σ2为大主应力σ1和小主应力σ3的平均值,即
(5)
(2)仓料类比砂性土,其黏聚力c=0。
(3)以压应力为正,拉应力为负。
2考虑中间主应力影响的侧压力系数
2.1D-P准则
D-P准则[11-14]属于广义Mises准则,视中间主应力与小主应力对材料强度的影响一样,其表达式为
(6)
(7)
I1=σ1+σ2+σ3
(8)
式中:J2为应力偏量第二不变量;I1为应力张量第一不变量。
将式(5),(7),(8)代入式(6),整理得基于D-P准则的侧压力系数kDP为
(9)
2.2M-N准则
M-N准则[15-19]是基于空间滑动理论提出的,适用于无黏性材料的强度准则,克服了M-C准则偏平面上的奇异性和D-P准则的拉压强度同性,并能在一定程度上反映材料强度的中间主应力效应。
M-N准则的表达式为
(10)
I2=σ1σ2+σ2σ3+σ3σ1
(11)
I3=σ1σ2σ3
(12)
式中:I2,I3分别为应力张量第二和第三不变量。
将式(5),(11),(12)代入式(10),可推得基于M-N准则的侧压力系数kMN为
(13)
2.3L-D准则
L-D准则[18-19]与M-N准则的表达式类似,但L-D准则的π平面极限线稍大于M-N准则。
L-D准则的表达式为
(1-sin(φ))]}
(14)
将式(5),(8),(12)代入式(14),可得基于L-D准则的侧压力系数kLD为
7sin(φ))-[(9-7sin(φ))(27(1-sin(φ))+
(15)
2.4UST理论
统一强度理论[20-21]可覆盖外凸强度准则上下限之间的所有区域,充分考虑了中间主应力效应及其区间性,可适用于各种不同拉压特性的材料。
UST理论的表达式为

(16)

(17)
式中:b为统一强度理论参数,反映的是中间主应力σ2对材料强度的影响程度,取值范围为0≤b≤1。
参数b与中间主应力σ2效应具有正相关性,b越大,中间主应力对材料强度的提高越多。同时,b也是选择强度准则的参数,b=0时统一强度理论退化为M-C准则,b=1时为双剪应力准则,0 由基本假定可知,式(17)满足平面应变状态。将式(5)代入式(17),可得基于UST理论的侧压力系数kUST为 (18) 将式(9),(13),(15),(18)分别代入式(1)和式(2),即可得到考虑中间主应力影响的4种真三轴强度准则所对应的深仓和浅仓侧压力计算公式,应用十分简洁、方便。 由筒仓侧压力计算理论[7]可知,仓料只会对仓壁产生挤压,即侧压力系数应为非负值,进而得到适用条件为 (19) 另外,4种真三轴强度准则的侧压力系数仅与仓料的内摩擦角φ有关。因此,仓料内摩擦角φ需满足隐式不等式(19)。对于不同的真三轴强度准则,只有当式(19)成立时,侧压力的计算结果才有效。经计算,对于D-P准则,仓料需满足内摩擦角φ≤42.22°,其余准则相应的仓料内摩擦角均无限值要求,适用条件较为广泛。 为探讨4种考虑中间主应力影响的真三轴强度准则在筒仓侧压力计算中的适用性,分别将其侧压力系数应用于深仓(H/D≥1.5,H,D分别为筒仓高度和内径)、浅仓(H/D<1.5)的侧压力计算,并将计算结果与试验实测值以及多国规范值进行比较和验证。 刘定华等[22]采用模型试验对圆筒煤仓仓壁的侧压力分布进行了测量,在仓壁埋设2列共12个压力传感器。模型筒仓为有机玻璃,仓壁高H=600 mm,内径D=300 mm,高径比H/D=2。仓料分别为末煤、小麦、干砂,末煤重度为10 kN·m-3,内摩擦角为33°,摩擦因数为0.45;小麦重度为8 kN·m-3,内摩擦角为28°,摩擦因数为0.4;干砂重度为16 kN·m-3,内摩擦角为32.5°,摩擦因数为0.43。 张家康等[23]给出了1组筒仓仓料侧压力实测数据,在仓壁埋设2列共10个土压力传感器。模型筒体为有机玻璃,仓身高H=564 mm,内径D=282 mm,高径比H/D=2。仓料为小米,重度为8.22 kN·m-3,内摩擦角为33°,摩擦因数为0.292。 3.1.1各准则对比 将文献[22],[23]共计4组试验数据与各准则计算结果进行比较,如图2所示。共讨论6种强度准则的计算结果,分别为D-P准则、M-N准则、L-D准则和统一强度理论UST(参数b=0,1/2,1),仅参数b=0时统一强度理论即M-C准则未考虑中间主应力的影响。 由图2可以看出:仓壁侧压力的强度准则效应显著,即不同强度准则计算的深仓侧压力差异显著;各准则计算的侧压力Ph呈现规律性变化,由大到小依次为UST理论(b=0)、UST理论(b=1/2)、M-N准则、UST理论(b=1)、L-D准则、D-P准则。文献[22]的3组试验中,各准则Ph计算值与试验实测值之比的平均值由大到小依次为1.21,1.10,1.07,1.03,0.97,0.70;文献[23]试验中,各准则Ph计算值与试验实测值之比的平均值由大到小依次为1.45,1.30,1.26,1.22,1.12,0.72。可见,由参数b=0时统一强度理论(未考虑中间主应力影响的M-C准则)得到的Ph最大,而D-P准则视中间主应力影响与小主应力影响相同,夸大了中间主应力对仓料强度的提高作用,计算得到的Ph最小,L-D准则计算的Ph与试验数据吻合最好,参数b=1/2时统一强度理论与M-N准则的Ph值较为接近。 3.1.2准则与规范对比 中国规范[8]采用的侧压力系数为Rankine主动土压力系数[式(3)],美国规范[24]采用的侧压力系数为静止土压力系数,即1-sin(φ),欧洲规范[25]以修正静止土压力系数1.1[1-sin(φ)]作为侧压力系数。 将深仓的4组试验数据与欧洲规范、美国规范、中国规范、中间主应力效应影响最小的UST理论(b=0)以及影响最大的D-P准则的Ph计算值进行比较,如图3所示。 由图3可以看出,计算的仓壁侧压力大小依次为欧洲规范、美国规范、中国规范、UST理论(b=0)、D-P准则;文献[22]的3组试验中,各规范和准则计算的Ph值与试验实测值之比的平均值从大到小依次为1.70,1.61,1.21,1.21,0.70。可见,各规范因未考虑中间主应力的影响均较为保守;参数b=0时统一强度理论(M-C准则)与中国规范计算的侧压力结果较一致;实测数据基本都分布于UST理论(b=0)曲线与D-P准则曲线所形成的区域之间,说明深仓侧压力计算中应合理考虑中间主应力的影响。 原方[26]对徐州国家粮食储备库储粮浅仓中的4号、7号、8号仓进行了实仓试验,筒仓内径D=30 m,高度H=15 m,存储高度分别为6.35,8,11.4 m;仓料为小麦,重度为7.88 kN·m-3,内摩擦角为25°,外摩擦角为21.8°;4号仓布置2排土压力传感器,7号和8号仓均布置1排。 陈长冰[27]选取河南省国家粮食储备库的4号仓作为试验仓,筒仓内径D=28 m,高度H=26 m,存储高度分别为6.3,13.5,22.3 m;仓料为小麦,重度为7.88 kN·m-3,内摩擦角为25°,外摩擦角为21.8°;沿仓壁共布设27个土压力传感器。 因不同存储高度下的筒壁侧压力分布规律类似,本节仅选取文献[26]中4号和7号仓的第1次和第2次试验,以及8号仓的第1次试验和文献[27]中4号仓第1次试验的实测数据进行验证。 3.2.1各准则对比 将浅仓6组试验数据与6种强度准则计算结果进行比较,如图4所示。由图4可知,无论是锥堆还是平堆,不同强度准则计算的浅仓侧压力之间的差异非常显著,侧压力由大到小依次为UST理论(b=0)、UST理论(b=1/2)、M-N准则、UST理论(b=1)、L-D准则、D-P准则,与深仓侧压力变化一致。6组试验中,各准则Ph计算值与试验实测值之比的平均值依次为1.21,1.09,1.07,1.01,1.00,0.82。参数b=0时统一强度理论(M-C准则)对应的Ph最大,D-P准则对应的Ph最小,始终小于试验数据;参数b=1/2时统一强度理论与M-N准则的Ph计算值较为接近,参数b=1时统一强度理论与L-D准则的Ph计算值较为接近;试验数据与L-D准则对应的Ph计算值吻合最好,二者之比平均为1.00。 3.2.2准则与理论对比 将6组浅仓试验数据与Rankine理论、修正Coulomb理论、中间主应力效应影响最小的UST理论(b=0)以及影响最大的D-P准则计算的Ph值进行比较,如图5所示。 由图5可知:计算的仓壁侧压力大小依次为修正Coulomb理论、Rankine理论、UST理论(b=0)、D-P准则;6组试验中,各理论和准则计算的Ph值与试验实测值之比的平均值从大到小依次为1.56,1.21,1.21,0.82。Rankine理论和修正Coulomb理论由于未考虑中间主应力的影响,计算的侧压力均较为保守;参数b=0时统一强度理论(M-C准则)与Rankine理论的结果相同;实测数据均分布在UST理论(b=0)与D-P准则的曲线之间,同样说明浅仓侧压力计算中合理考虑中间主应力影响的必要性。 (1)根据筒仓侧压力原理和基本假定,本文基于D-P准则、M-N准则、L-D准则和统一强度理论,推导了平面应变状态下4种考虑中间主应力影响的侧压力系数,除应用D-P准则时仓料内摩擦角应不大于42.22°以外,其他3种准则均无限制要求,适用条件较为广泛,且侧压力计算公式应用简洁、方便,并与深仓、浅仓侧压力的文献实测数据和多国规范值进行了比较及验证。 (2)对于深仓侧压力,欧洲规范计算结果最为保守,美国规范次之,中国规范与参数b=0时统一强度理论的结果相同;参数b=1/2时统一强度理论与M-N准则的结果较为接近。对于浅仓侧压力,修正Coulomb理论最为保守,Rankine理论与参数b=0时统一强度理论的结果相同;参数b=1/2时统一强度理论与M-N准则的结果较为接近;参数b=1时统一强度理论与L-D准则的结果较为接近。 (3)深仓和浅仓侧压力计算的强度准则效应均很显著,本质反映的是不同准则对中间主应力影响的不同考虑;参数b=0时统一强度理论(M-C准则)由于不能考虑中间主应力的影响,所对应的结果偏于保守,而D-P准则视中间主应力影响与小主应力影响相同,得到的结果偏于危险;L-D准则合理考虑了仓料强度的中间主应力效应,整体上与实测数据吻合最好,应优先考虑选用。 参考文献: References: [1] DOGANGUN A,KARACA Z,DURMUS A,et al.Cause of Damage and Failures in Silo Structures[J].Journal of Performance of Constructed Facilities,2009,23(2):65-71. [2] SADOWSKI A J,ROTTER J M.Exploration of Novel Geometric Imperfection Forms in Buckling Failures of Thin-walled Metal Silos Under Eccentric Discharge[J].International Journal of Solids and Structures,2013,50(5):781-794. [3] TANG G,YIN L,LI Z,et al.Structural Performance of Double-wall Steel Insulation Silo with Multiple Bolted Joints[J].Journal of Constructional Steel Research,2017,139:411-423. [4] 孙珊珊,赵均海,张常光,等.深仓和浅仓储料侧压力新解[J].广西大学学报:自然科学版,2018,43(1):168-177. SUN Shan-shan,ZHAO Jun-hai,ZHANG Chang-guang,et al.New Solution for Lateral Pressure of Silos and Bunkers[J].Journal of Guangxi University:Natural Science Edition,2018,43(1):168-177. [5] 周长东,郭坤鹏,孟令凯,等.钢筋混凝土筒仓-散料的静力相互作用分析[J].同济大学学报:自然科学版,2015,43(11):1656-1661,1669. ZHOU Chang-dong,GUO Kun-peng,MENG Ling-kai,et al.Static Interaction Analysis of RC Silo Structure-granular Material[J].Journal of Tongji University:Natural Science,2015,43(11):1656-1661,1669. [6] WANG Y,LU Y,JIN O Y.A Numerical Study of Wall Pressure and Granular Flow in a Flat-bottomed Silo[J].Powder Technology,2015,282(24):43-54. [7] 付建宝.大直径筒仓的侧压力分析与筒仓地基三维固结分析[D].大连:大连理工大学,2012. FU Jian-bao.Lateral Wall Pressure Analysis and Three-dimensional Foundation Consolidation Analysis of Large Diameter Silos[D].Dalian:Dalian University of Technology,2012. [8] GB 50077—2003,钢筋混凝土筒仓设计规范[S]. GB 50077—2003,Code for Design of Reinforced Concrete Silos[S]. [9] XU S Q,YU M H.The Effect of the Intermediate Principal Stress on the Ground Response of Circular Openings in Rock Mass[J].Rock Mechanics and Rock Engineering,2006,39(2):169-181. [10] 俞茂宏.线性和非线性的统一强度理论[J].岩石力学与工程学报,2007,26(4):662-669. YU Mao-hong. Linear and Nonlinear Unified Strength Theory[J]. Chinese Journal of Rock Mechanics and Engineering,2007,26(4):662-669. [11] 姜福兴,刘金海,王 平.基于Druker-Prager准则的煤层冲击失稳模型[J].煤炭学报,2011,36(5):727-731. JIANG Fu-xing,LIU Jin-hai,WANG Ping.Model of Coal Burst and Instability Based on Drucker-Prager Yield Criterion[J].Journal of China Coal Society,2011,36(5):727-731. [12] 赵尚毅,郑颖人,刘明维,等.基于Drucker-Prager准则的边坡安全系数定义及其转换[J].岩石力学与工程学报,2006,25(增1):2730-2734. ZHAO Shang-yi,ZHENG Ying-ren,LIU Ming-wei,et al.Definition and Transformation of Slope Safety Factor Based on Drucker-Prager Criterion[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(S1):2730-2734. [13] ALEJANO L R,BOBET A.Drucker-Prager Criterion[J].Rock Mechanics and Rock Engineering,2012,45(6):995-999. [14] JIANG H,XIE Y L.A Note on the Mohr-Coulomb and Drucker-Prager Strength Criteria[J].Mechanics Research Communications,2011,38(4):309-314. [15] 赵春风,杨砚宗,张常光,等.考虑中主应力的常用破坏准则适用性研究[J].岩石力学与工程学报,2011,30(2):327-334. ZHAO Chun-feng,YANG Yan-zong,ZHANG Chang-guang,et al.Investigation on Applicability of Common Failure Criteria Considering Intermediate Principal Stress[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(2):327-334. [16] 张常光,晏 青,张成林.考虑中间主应力的路堤临界填土高度统一解及比较[J].岩石力学与工程学报,2016,35(7):1466-1473. ZHANG Chang-guang,YAN Qing,ZHANG Cheng-lin.A Unified Solution of Critical Filling Height for Embankment Considering Intermediate Principal Stress and Its Comparisons[J].Chinese Journal of Rock Mechanics and Engineering,2016,35(7):1466-1473. [17] LIU M C,GAO Y F,LIU H L.A Nonlinear Drucker-Prager and Matsuoka-Nakai Unified Failure Criterion for Geomaterials with Separated Stress Invariants[J].International Journal of Rock Mechanics and Mining Sciences,2012,50:1-10. [18] 郭力群,蔡奇鹏,彭兴黔.条带煤柱设计的强度准则效应研究[J].岩土力学,2014,35(3):777-782. GUO Li-qun,CAI Qi-peng,PENG Xing-qian.Effect of Strength Criterion on Design of Strip Coal Pillar[J].Rock and Soil Mechanics,2014,35(3):777-782. [19] 姜 华.基于等效Mohr-Coulomb摩擦角的强度准则主应力平面表示[J].中南大学学报:自然科学版,2012,43(8):3216-3221. JIANG Hua.Expressing Strength Criterion in Principal Stress Plane Base on Equivalent Mohr-Coulomb Friction Angle[J].Journal of Central South University:Science and Technology,2012,43(8):3216-3221. [20] 俞茂宏.双剪理论及其应用[M].北京:科学出版社,1998. YU Mao-hong.Twin-shear Theory and Its Application[M].Beijing:Science Press,1998. [21] 孙珊珊,赵均海,张常光,等.基于统一强度理论的大型浅圆筒仓侧压力计算[J].工程力学,2013,30(5):244-249. SUN Shan-shan,ZHAO Jun-hai,ZHANG Chang-guang,et al.Lateral Pressure of Large Squat Silos Based on the Unified Strength Theory[J].Engineering Mechanics,2013,30(5):244-249. [22] 刘定华,郝际平.钢筋混凝土筒仓仓壁侧压力的研究[J].建筑结构学报,1995,16(5):57-63. LIU Ding-hua,HAO Ji-ping.Research on Lateral Pressure Upon Wall of Reinforced Concrete Silo[J].Journal of Building Structures,1995,16(5):57-63. [23] 张家康,黄文萃,姜 涛,等.筒仓贮料侧压力系数研究[J].建筑结构学报,1999,20(1):71-74. ZHANG Jia-kang,HUANG Wen-cui,JIANG Tao,et al.Study on Lateral Pressure Ratio of Stored Material in Silos[J].Journal of Building Structures,1999,20(1):71-74. [24] ACI 313-97,Standard Practice for Design and Construction of Concrete Silos and Stacking Tubes for Storing Granular Materials[S]. [25] EN 1998-4-2007,Eurocode 8:Design of Structure for Earthquake Resistance — Part 4:Silos,Tanks and Pipelines[S]. [26] 原 方.曲线挡墙内侧散粒体压力分析及工程应用[D].大连:大连理工大学,2004. YUAN Fang.Pressure Analysis and Engineering Application of Granular Solids on the Inner Side of Curved Retaining Wall[D].Dalian:Dalian University of Technology,2004. [27] 陈长冰.筒仓内散体侧压力沿仓壁分布研究[D].合肥:合肥工业大学,2006. CHEN Chang-bing.Research on Distribution of Lateral Bulk-solid Pressures on Silos’ Wall[D].Hefei:Hefei University of Technology,2006.2.5适用条件
3对比和讨论
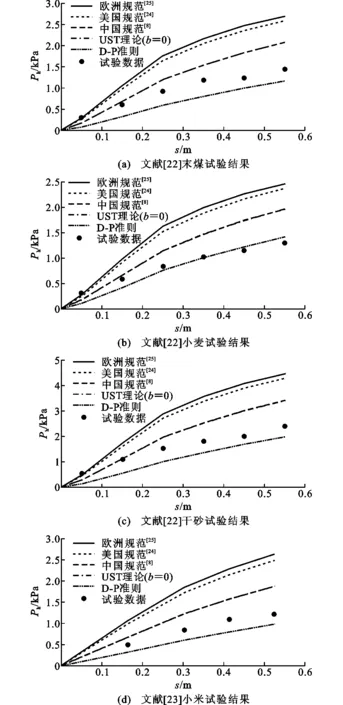
3.1深 仓



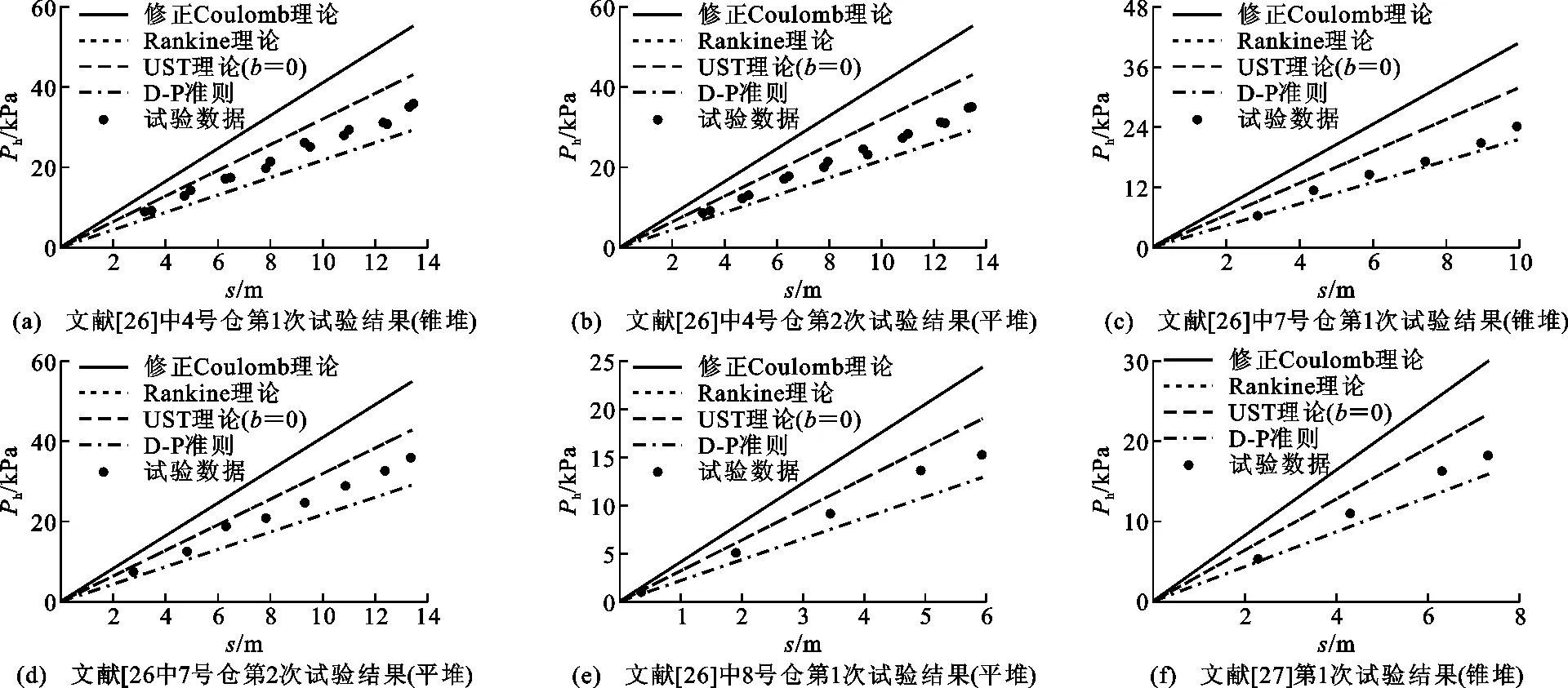
3.2浅 仓



4结语

