附加油阻尼器的非线性滞回结构系统的等价线性化方法

蒲武川，李 琪

(武汉理工大学 土木工程与建筑学院，湖北 武汉 430070)

0引 言

耗能减震技术的理论研究和实际工程运用在中国已得到极大发展。建筑结构中安装的耗能装置利用材料屈服或流体运动产生阻尼力，并以此耗散地震能量，达到减小地震引起的结构振动或损伤的目的。油阻尼器利用油性材料流动产生的节流阻抗作为阻尼力，其阻尼力与运动速度呈比例。油阻尼器一般还设置溢流阀，当阻尼力达到一定阈值后，溢流阀启动，阻尼系数降低，阻尼力随速度的变化减慢。因此，油阻尼器的力-速度关系表现出双线性特征。该特征可以抑制过高阻尼力的产生，避免结构中产生过大的水平剪力[1-2]。

油阻尼器用于结构抗震有较高的优越性，近年不断有新型油阻尼器、新的设计和分析方法得到开发和研究[3-5]。油阻尼器力学性能的理论计算较为复杂[6-8]，日本隔震结构协会提出将其双线性的力-速度关系等价为线性关系的方法，推导出了等价黏滞系数的计算公式[9]。等价线性黏滞系统中黏滞单元最大速度与原双线性黏滞系统的黏滞单元最大速度接近，可由线性黏滞系统近似预测双线性黏滞系统在地震作用下的最大位移，但是该方法针对线弹性主体结构提出，其适用范围有限。类似的等价线性化方法也被开发并应用于桥梁结构斜拉索振动的油阻尼器控制中[10]。近年发生的大地震中油阻尼器的破坏案例[11]表明，针对大震选择恰当的性能目标并进行合理的结构减震设计非常重要。在基于目标位移的性能化设计中，考虑罕遇地震作用，将结构弹塑性位移作为目标位移的设计越来越多[12-15]。当油阻尼器应用于该类非线性主体结构时，结构系统同时包含非线性黏滞单元和非线性主体结构，该类双非线性结构系统的等价线性化方法需要进一步研究。

本文以附加油阻尼器的非线性滞回结构系统为研究对象，基于稳态响应对结构系统等价线性化参数进行推导，并基于动力时程分析对参数进行修正，建立其等价线性化模型。基于等价模型对地震作用下多种参数组合的非线性结构系统的地震位移响应进行估算，验证模型精度，并基于等价模型扩展了非线性结构系统的性能曲线，为该类结构系统的减震设计应用提供参考。

1油阻尼器及结构系统的滞回特征

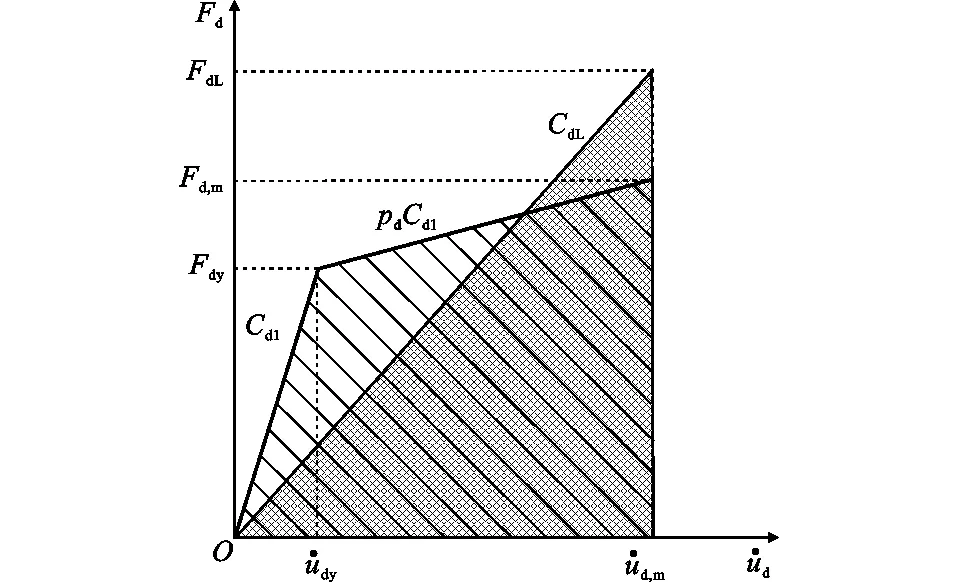
1.1油阻尼器模型及滞回特征

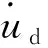
(1)

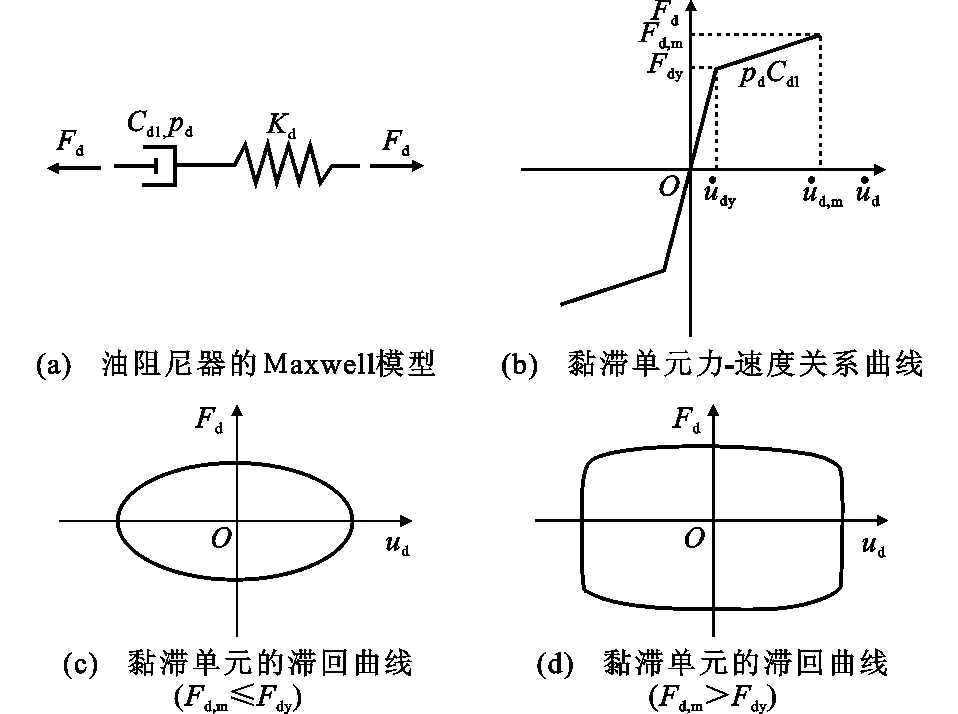
图1(c)，(d)分别表示了溢流前后黏滞单元典型的阻尼力-位移关系曲线。

1.2结构系统的构成及滞回特征

2等价线性化参数的推导

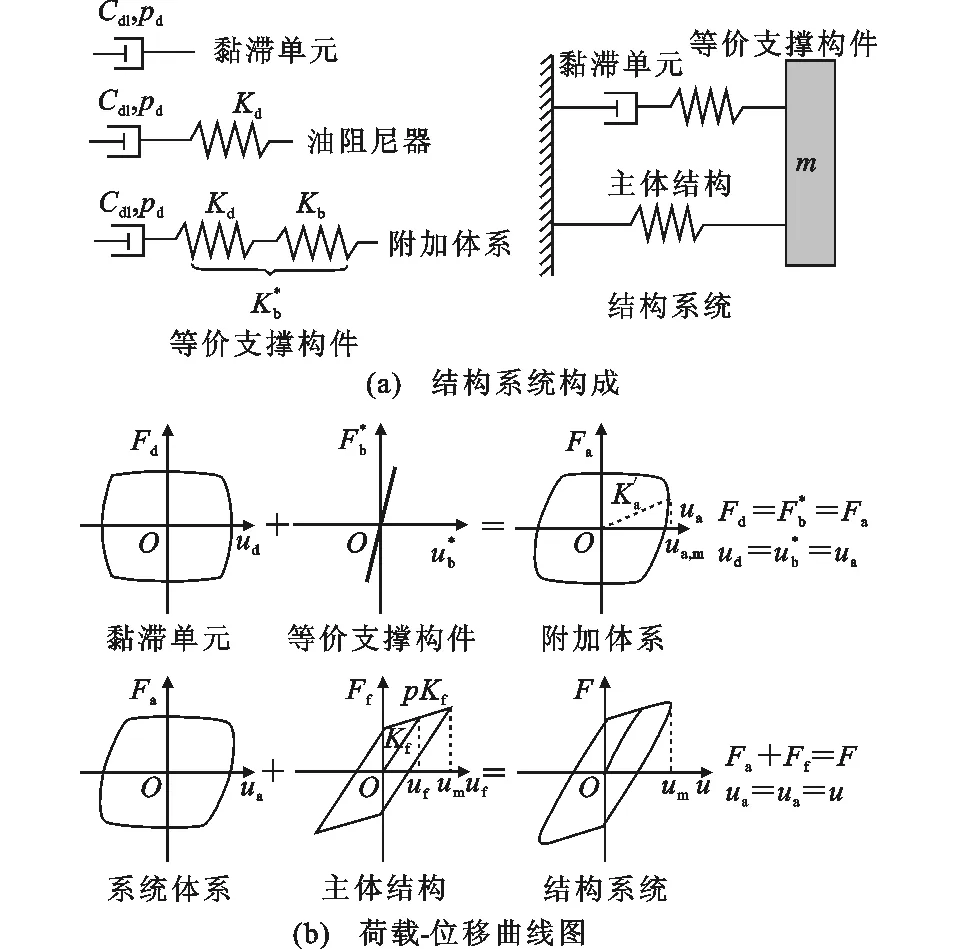
2.1主体结构弹性状态时结构系统的等价线性化

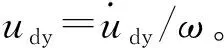
(2)

考虑结构系统处于简谐振动的状态，位移u=umsin(ωt)(t为时间)，等价后附加体系最大位移um与黏滞单元最大位移ud,m之间的关系近似表示为

(3)

(4)

一个稳态循环中，附加体系与黏滞单元的滞回耗能相等，阻尼器的滞回耗能Epd可表示为

(5)

2.2主体结构弹塑性变形时结构系统等价线性化

当系统位移超过主体结构屈服位移后，主体结构的抗力与位移也呈非线性关系。对该状态下的结构系统进行等价线性化处理需同时考虑主体结构和非线性黏滞单元的线性化处理。

首先对主体结构采用常规的等价线性化方法[16-17]，将其等价为线性黏滞单元和线性弹簧单元构成的Kelvin模型。以其最大位移对应的割线刚度Keq,f作为主体结构的等价刚度，表示为

Keq,f=Kf(1+pμ-p)/μ

(6)

主体结构在一个稳态循环中耗能Epf由式(7)计算，即

(7)

激励频率与割线刚度对应的结构自振频率相等时，假设线性黏滞单元耗能与主体结构滞回耗能相等，可得线性黏滞单元的阻尼系数Cf为

(8)

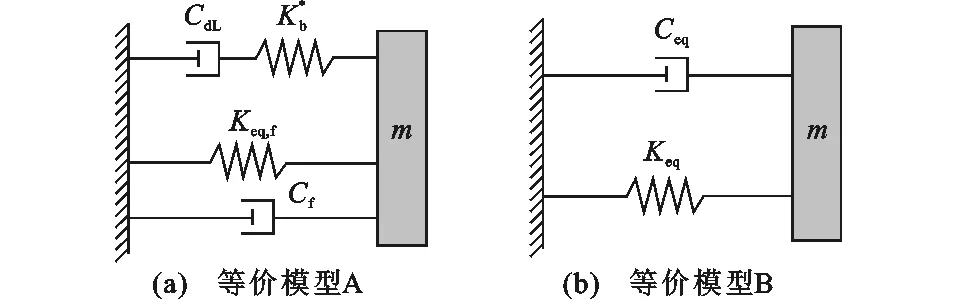
图4为等价模型示意，其中Ceq为阻尼系数，Keq为主体结构刚度。在主体结构等价为Kelvin模型的基础上，对附加体系分两步等价。首先采用第2.1节所述方法，将双线性黏滞单元等价为线性黏滞单元，并将含线性黏滞单元的附加体系与主体结构的等价Kelvin模型并联构成系统的等价模型A，如图4(a)所示。线性黏滞单元黏滞系数CdL采用式(2)计算，当激励频率未知时μd采用主体结构自振频率ωeq,f计算。

由于式(2)原本基于弹性结构系统提出[9]，为验证该方法对弹塑性主体结构的适用性，对非线性结构系统和对应的等价模型A绘制共振曲线并进行比较。采用时程分析软件PC-ANSR[18]建立如图2(a)所示单自由度结构系统，参数设置如表1所示，其中ξ=Cd1/(2mωf)，Kb=Kf，Kd=βCd1，β为阻尼器内部刚度系数，ξ0为结构初始黏滞阻尼比。对结构施加正弦波激励，得到最大位移um，由前述方法建立等价模型A。图5对比了原非线性结构系统和等价模型A的共振曲线，竖虚线左侧表示油阻尼器未进入双线性状态，其中T为周期，竖虚线右侧表示油阻尼器进入了双线性状态。油阻尼器是否进入双线性状态直接通过比较时程分析中黏滞单元的最大速度与溢流速度进行判定。从图5可以看出，模型A与原结构的共振曲线均基本吻合，等价线性黏滞系数CdL的求解方法可行。

表1单自由度结构系统参数Tab.1Parameters of SDOF Structural System

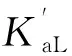
(9)

主体结构和附加体系的应变能Esf，Esa分别由式(10)和(11)求得

(10)

(11)

(12)

(13)

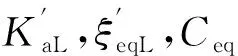
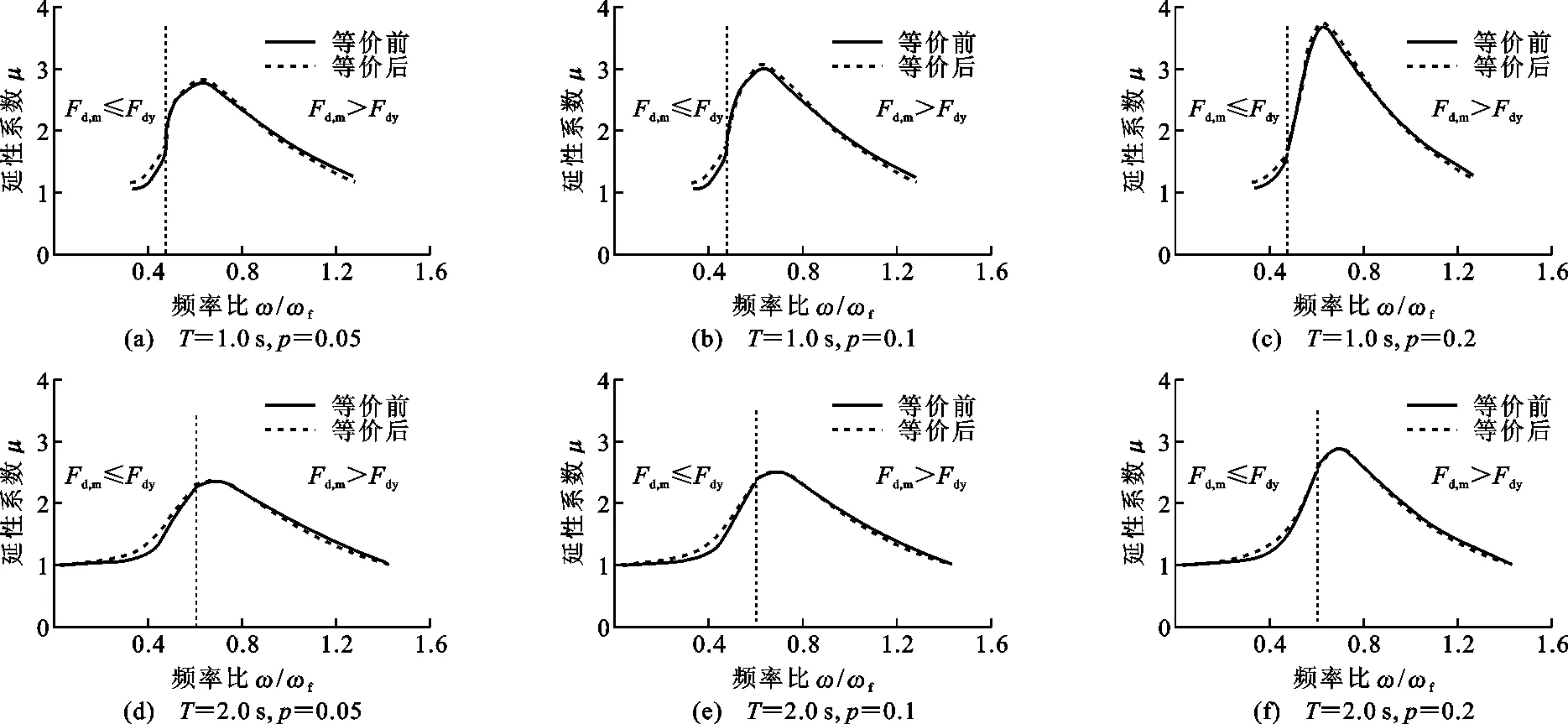
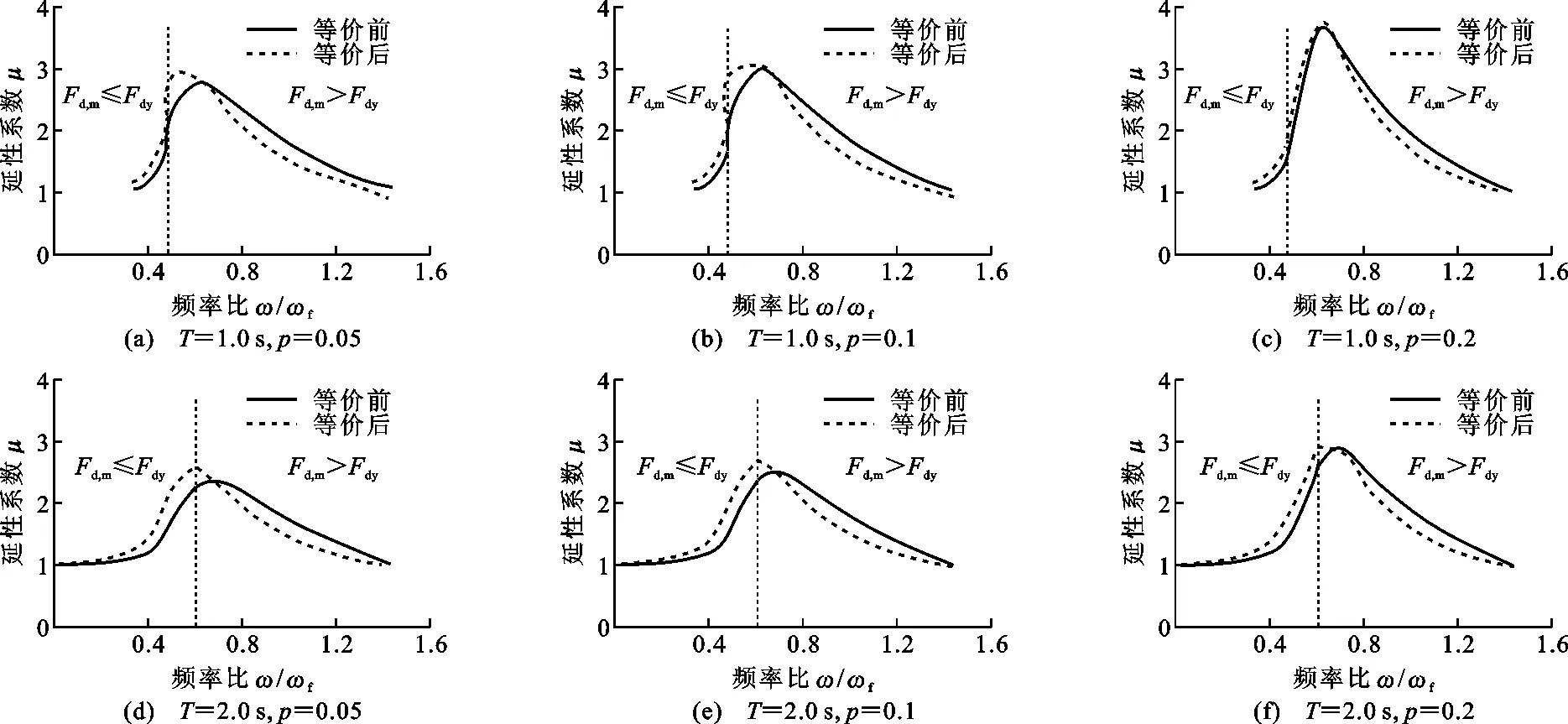
采用与图5相同的结构参数，图6对比了非线性结构系统与等价模型B的共振曲线。从图6可以看出，模型B与原结构的共振曲线也基本吻合，但相对于模型A来说模型B精度略为降低，这是由于将附加体系的Maxwell模型等价成Kelvin模型引起的。

3地震作用下等价阻尼比的修正

3.1考虑地震作用的等价阻尼比修正

(14)

ξop按照以下步骤计算：对设定的结构模型输入地震波计算其最大位移um，按照式(9)计算Keq及对应的等价周期Teq,从地震波位移反应谱(阻尼比从0.01到0.5，按0.01递增)中找出对应于Teq且位移值最接近um的阻尼比，该阻尼比即为等价模型与原结构最大位移等价的最优阻尼比ξop。

假设Tf=0.4，0.8，1.0，2.0 s，p=0.05，0.1，0.2，结构弹性状态下油阻尼器附加阻尼比为0.1，主体结构目标延性系数μ=1，2，3，4，考虑各参数间的不同组合，共48种工况。输入表2中所示8条地震波，通过调整地震波放大倍数使结构延性系数达到目标值。按照前述流程求得α，并将其作为延性系数和等价周期的函数进行回归，得到α的近似表达式，如式(15)所示，并最终得到等价结构系统在地震作用下的等价阻尼比计算公式，如式(16)所示

(15)

(16)

3.2基于反应谱的地震响应预测

设定主体结构参数如表1所示，采用表2中的地震波，调整地震波放大倍数并作用于结构系统，使主体结构延性系数分别达到1，2，3，4；计算地震波对应于结构初始黏滞阻尼比ξ0=0.02的位移反应谱；根据延性系数计算结构系统的等价周期Teq和等价阻尼比ξeq，根据Teq在位移反应谱中找到对应的反应谱值，将其乘以式(17)所示阻尼调整系数CDMF[16]及地震波放大倍数得到位移预测值。

(17)

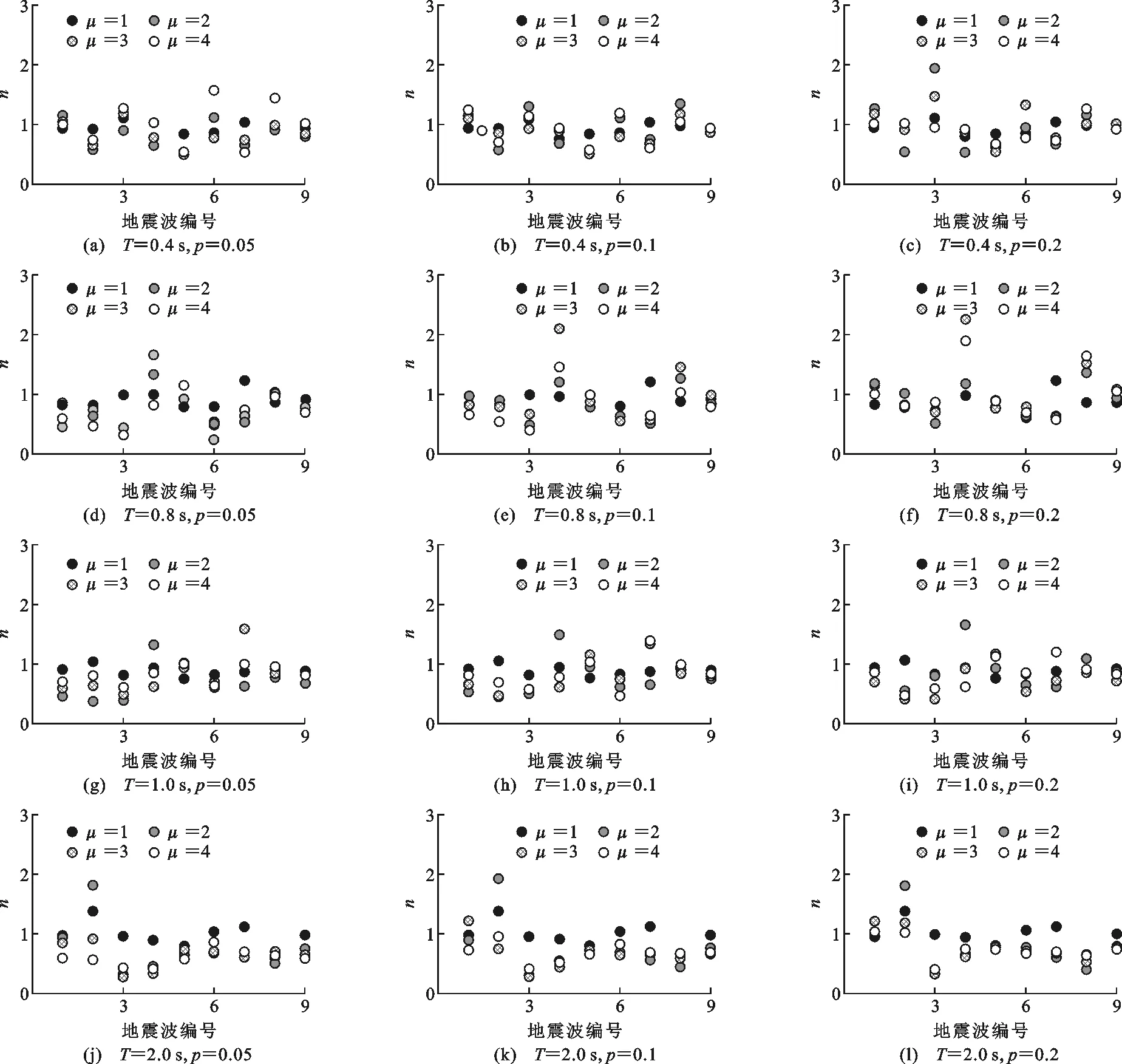
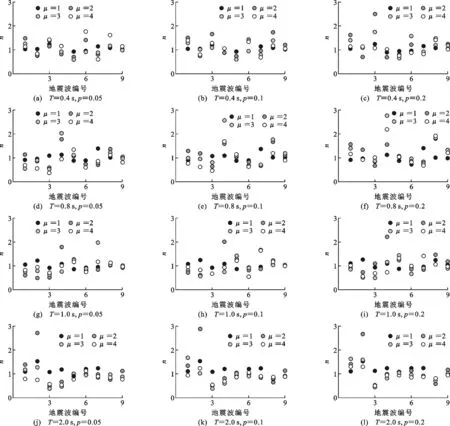
图7，8给出了结构系统最大位移预测值与时程分析值的比值n，其中地震波编号9表示8条地震波计算结果的平均值。图7的位移预测值采用未修正的阻尼比[式(12)]计算得到，图8采用修正的阻尼比[式(16)]计算得到。从图7可以看出，预测值与时程分析值的比值分布在0.5～1.0之间，未修正阻尼比由于过高估计结构系统的阻尼比，导致过低估计结构响应。图7中所有预测值与时程分析值的

比值平均为0.851，方差为0.09。图8中所有比值平均为1.044，方差为0.14。修正后等价阻尼比在平均意义上能更好地预测地震作用下非线性结构系统的最大位移。

作为示例，选取Tf=1 s,p=0.05,μ=2的工况，将表2中第1，2条地震波作用下的位移时程曲线绘制于图9。图9中，模型B与原结构的最大位移接近，等价模型不能模拟结构的残余变形。

4基于等价模型的减震性能曲线

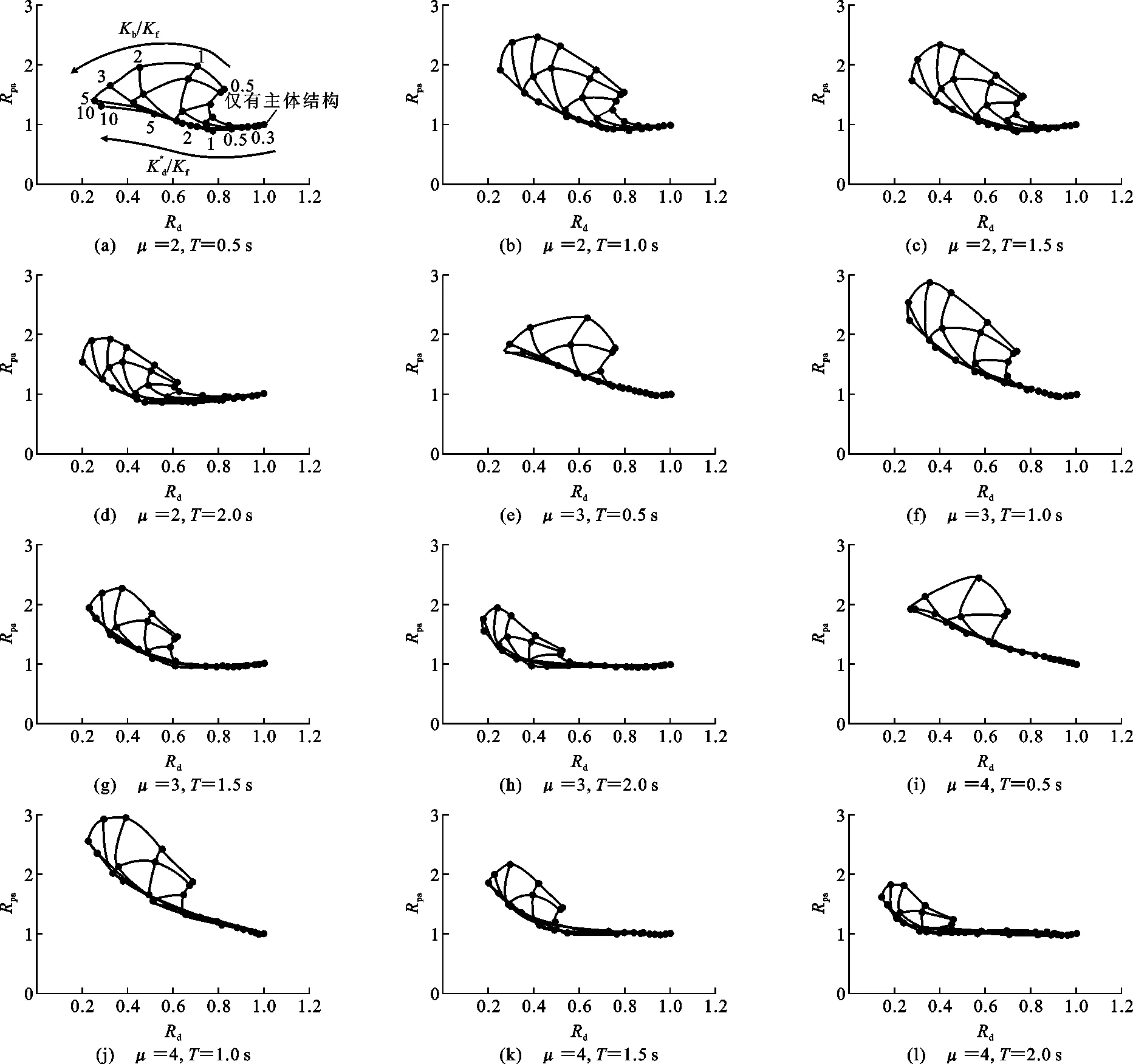
文献[9]中建立了减震结构的减震性能曲线，用结构响应降低率直观描述阻尼器参数对减震结构性能的影响，减震性能曲线还可用于减震设计，以确定对应于减震性能目标的阻尼器参数。基于本文所述等价线性化方法，将性能曲线扩展到附加油阻尼器的非线性结构中，通过以下步骤绘制性能曲线。

定义安装油阻尼器的非线性减震控制结构与无控非线性结构的位移Sd、拟加速度Spa的比值分别为位移降低率Rd、拟加速度降低率Rpa，如式(18)，(19)所示

(18)

(19)

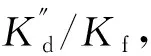
(20)

(21)

(22)

根据文献[9]推荐，为控制λ的取值以保证阻尼器足够的变形，取βTeq,f≈16。另外，由式(23)近似求得λL

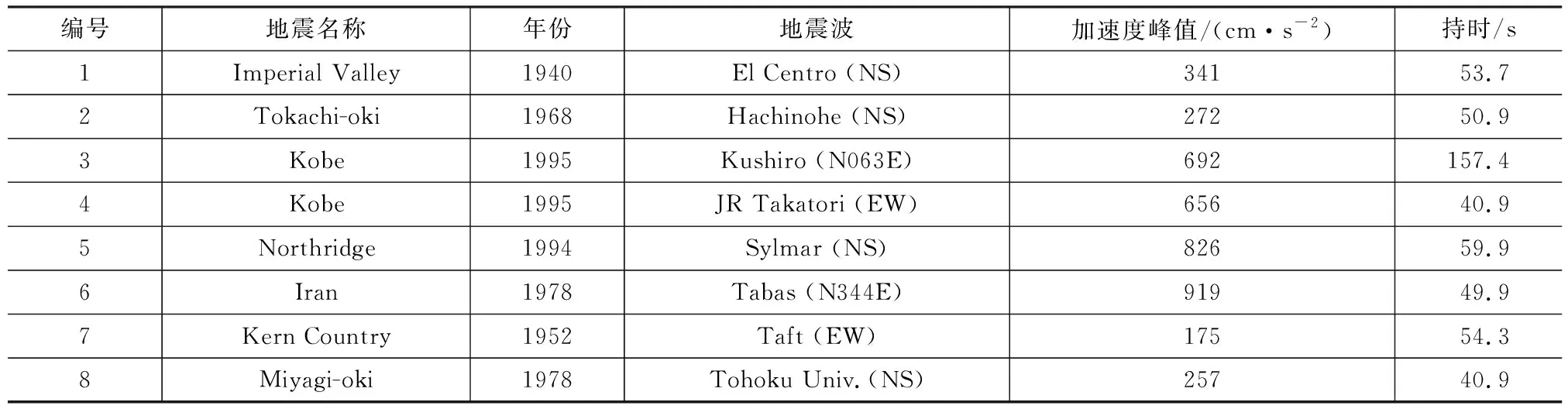
表2地震波信息Tab.2Information of Input Ground Motions

(23)

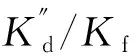
5结语

(1)模型A与原结构共振曲线吻合，表明本文所述非线性结构系统中将双线性黏滞单元等价为线性黏滞单元的方法可行，可实现双线性黏滞单元的线性化。

(2)模型B与原结构共振曲线基本吻合，表明推导的等价阻尼比和等价周期较好地代表了结构系统的动力特性，在结构位移计算上该模型与原非线性结构系统具有等价性。

(3)考虑地震作用对稳态响应阻尼比进行修正后，等价模型位移预测值与时程分析值比值的均值为1.044，方差为0.14，等价线性化模型可有效地用于地震位移预测。

(4)将等价线性化方法应用于性能曲线，建立了非线性减震控制结构相对于非线性无控结构响应比值的性能曲线，可有效辅助设计人员进行非线性结构减震设计。

参考文献：

References:

[1] ADACHI F,FUJITA K,TSUJI M,et al.Importance of Interstory Velocity on Optimal Along-height Allocation of Viscous Oil Dampers in Super High-rise Buildings[J].Engineering Structures,2013,56:489-500.

[2] ADACHI F,YOSHITOMI S,TSUJI M,et al.Nonlinear Optimal Oil Damper Design in Seismically Controlled Multi-story Building Frame[J].Soil Dynamics and Earthquake Engineering,2013,44:1-13.

[3] YAMAMOTO M,MINEWAKI S,NAKAHARA M,et al.Concept and Performance Testing of a High-capacity Oil Damper Comprising Multiple Damper Units[J].Earthquake Engineering & Structural Dynamics,2016,45:1919-1933.

[4] 杨巧荣,孔令祥,郭 彦,等.位移放大型油阻尼器减震结构减震效应分析[J].地震工程与工程振动,2017,37(1):48-55.

YANG Qiao-rong,KONG Ling-xiang,GUO Yan,et al.Vibration Reduction Effect Analysis of Building Structure Equipped with Displacement Amplification Oil Damper[J].Earthquake Engineering and Engineering Dynamics,2017,37(1):48-55.

[5] 杨朋超,薛松涛,谢丽宇.地震动作用下消能构件的动力可靠性分析[J].土木工程学报,2016,49(增1):114-118,130.

YANG Peng-chao,XUE Song-tao,XIE Li-yu.Dynamic Reliability Analysis of Passive Energy Dissipation Devices Subjected to Seismic Excitations[J].China Civil Engineering Journal,2016,49(S1):114-118,130.

[6] KASAI K,MATSUDA K.Full-scale Dynamic Testing of Response-controlled Buildings and Their Components:Concepts,Methods,and Findings[J].Earthquake Engineering and Engineering Vibration,2014,13(S1):167-181.

[7] TSUYUKI Y,GOFUKU Y,IIYAMA F,et al.JSSI Manual for Building Passive Control Technology Part3 Performance and Quality of Oil Damper[C]//WCEE.Proceedings of 13th World Conference on Earthquake Engineering.Vancouver:WCEE,2004:2468.

[8] KASAI K,ITO H,OOKI Y,et al.Full-scale Shake Table Tests of 5-story Steel Building with Various Dampers[C]//CUEE.Proceedings of the 7th International Conference on Urban Earthquake Engineering & 5th International Conference on Earthquake Engineering.Tokyo:CUEE,2010:11-22.

[9] 日本隔震结构协会.被动减震结构设计·施工手册[M].蒋 通,译.2版.北京：中国建筑工业出版社,2008.

Japan Society of Seismic Isolation.Passive Damping Structure Design and Construction Manual[M].Translated by JIANG Tong.2nd ed.Beijing:China Architecture & Building Press,2008.

[10] 周海俊,孙利民.附加双线性油阻尼器斜拉索的阻尼特性研究[J].振动与冲击,2010,29(3):1-4,33.

ZHOU Hai-jun,SUN Li-min.Damping of Taut Cable with Attached Bilinear Viscous Damper[J].Journal of Vibration and Shock,2010,29(3):1-4,33.

[11] 谢丽宇,唐和生,薛松涛.首例油阻尼器破坏对结构设计的经验教训——日本3·11地震的启示[J].结构工程师,2015,31(2):2-9.

XIE Li-yu,TANG He-sheng,XUE Song-tao.Lessons Learned for Design of Passively-controlled Structures from the Great East Japan Earthquake[J].Structural Engineers,2015,31(2):2-9.

[12] 吴学淑.基于设计使用年限和位移的耗能减震加固设计[J].建筑结构,2010,40(增2):99-102.

WU Xue-shu.Seismic Retrofit with Dampers Considering Design Working Life and Displacement[J].Building Structure,2010,40(S2):99-102.

[13] PRIESTLEY M J N.Direct Displacement-based Design of Precast/Prestressed Concrete Buildings[J].PCI Journal,2002,47(6):66-79.

[14] 简 斌,翁 健,金云飞.直接基于位移的预应力混凝土框架结构抗震设计方法[J].工程力学,2010,27(7):205-211,225.

JIAN Bin,WENG Jian,JIN Yun-fei.Direct Displacement-based Seismic Design for Prestressed Concrete Frame Structures[J].Engineering Mechanics,2010,27(7):205-211,225.

[15] 胡宝琳,姚文娟,李国强.罕遇地震荷载作用下屈曲约束支撑框架结构弹塑性位移的简化计算方法[J].振动与冲击,2011,30(2):144-148.

HU Bao-lin,YAO Wen-juan,LI Guo-qiang.A Simplified Calculation Method for Solving Elasoplastic Displacement of a Buckling-restrained Braced Frame Under Severe Earthquakes[J].Journal of Vibration and Shock,2011,30(2):144-148.

[16] KASAI K,ITO H,WATANABE A.Peak Response Prediction Rule for a SODF Elasto-plastic System Based on Equivalent Linearization Technique[J].Journal of Structural and Construction Engineering,2003,571:53-62.

[17] 蒲武川,梁瑞军,刘传奇,等.基于位移和等价刚度的建筑结构减震控制设计[J].建筑结构学报,2016,37(增1):71-78.

PU Wu-chuan,LIANG Rui-jun,LIU Chuan-qi,et al.Seismic Control Design of Building Structure Based on Displacement and Equivalent Stiffness[J].Journal of Building Structures,2016,37(S1):71-78.

[18] MAISON B F.PC-ANSR:A Computer Program for Nonlinear Structural Analysis[R].Berkeley:University of California,1992.

[19] GB 50011—2010,建筑抗震设计规范[S].

GB 50011—2010,Code for Seismic Design of Buildings[S].