函数性质融合的高考题型面面观

杜红全

(甘肃省康县教育局教研室 746500)

函数的性质是高考的重点内容之一，函数的单调性和奇偶性是高考的热点.高考中对函数性质的考查往往不是单纯地考查一个性质，而是综合考查.

一、单调性与奇偶性融合

例1 (2017全国)函数f(x)在(-∞,+∞)单调递减，且为奇函数．若f(1)=-1，则满足-1≤f(x-2)≤1的x的取值范围是( )

A．[-2,2] B．[-1,1]

C．[0,4] D.[1,3]

解析：因为函数f(x)为奇函数，f(1)=-1，所以

f(-1)=1.又f(x)在(-∞,+∞)单调递减，所以由-1≤f(x-2)≤1可得-1≤x-2≤1，解得1≤x≤3.故选D.

点评本题主要考查函数的单调性、奇偶性、函数值等知识，考查抽象概括能力和运算能力.做本题的关键是利用函数奇偶性把-1≤f(x-2)≤1转化为f(1)≤

f(x-2)≤f(-1),再利用函数的单调性去掉函数符号“f”，转为不等式-1≤x-2≤1.

二、单调性与对称性融合

例2 (2017年全国)已知函数f(x)=lnx+ln(2-x)，则( )

A．f(x)在(0,2)单调递增

B．f(x)在(0,2)单调递减

C．y=f(x)的图象关于直线x=1对称

2）关系曲线符号检验、适线检验和偏离值检验均小于《水文资料整编规范》（GB50179-2015）3.4.1规定。

D．y=f(x)的图象关于点(1,0)对称

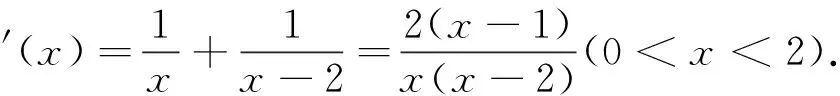
点评本题主要考查函数与导数、函数单调性、函数对称性等知识，考查数形结合的数学思想与运算能力;解本题的关键是运用排除法以及对原解析式进行变形;此题也可以代入特殊值，例如x=0.5,x=1.5进行判断，可以迅速得到答案.

三、奇偶性与对称性融合

例3 (2014年全国)偶函数y=f(x)的图象关于直线x=2对称，f(3)=3，则f(-1)=______.

解析因为函数y=f(x)是偶函数，所以f(-1)=f(1)，又因函数y=f(x)的图象关于直线x=2对称，所以f(1)=f(3)，因此f(-1)=f(1)=f(3)=3.

点评本题主要考查偶函数和函数对称性的性质；解本题的关键是根据函数的对称性和奇偶性进行转化.

四、奇偶性与周期性融合

解析因为f(x+4)=f(x-2)，所以f(x+6)=f(x)，所以T=6.所以f(919)=f(153×6+1)=

f(1).因为f(x)是偶函数,所以f(1)=f(-1).因为当x∈[-3,0]时,f(x)=6-x,所以f(919)=f(1)=f(-1)=6-(-1)=6.

点评本题主要考查函数的奇偶性、周期性以及求函数值问题.解本题的关键是周期的转化和代入求值的区间的转化.

五、单调性、奇偶性与周期性融合

例5 (2013年湖北)x为实数,[x]表示不超过x的最大整数，则函数f(x)=x-[x]在R上为( )

图1

A.奇函数 B.偶函数

C.增函数 D.周期函数

解析作出函数的大致图象如下图，通过观察图象，不难发现函数 是周期函数.故选D.

点评本题主要考查分段函数的性质、函数的周期以及数形结合的数学思想. 解本题的关键是作出函数的大致图象，通过图象直观来判断.

参考文献：

[1]杜红全.追踪考题:晒晒考点—解析几何考点题型归类解析[J].数理化解题研究(高中版),2016(02).