粒子群空间优化的端元提取算法

祝章智，黄风华

ZHU Zhangzhi1，2，3,HUANG Fenghua1

1.福州大学 福建省空间信息工程研究中心，福州 350002

2.福州大学 空间数据挖掘与信息共享教育部重点实验室，福州 350002

3.福州大学 地理空间信息技术国家地方联合工程研究中心，福州 350002

1.Provincial Spatial Information Engineering Research Center,Fuzhou University,Fuzhou 350002,China

2.Key Laboratory of Spatial Data Mining and Information Sharing of Ministry of Education,Fuzhou University,Fuzhou 350002,China

3.National Engineering Research Centre of Geospatial Space Information Technology,Fuzhou University,Fuzhou 350002,China

高光谱遥感技术是将目标探测与光谱成像相结合的地物信息识别技术，它以其精细的光谱分辨能力改变着人类观察地表的视角。但是，由于地物分布的复杂性及传感器空间分辨率的限制，混合像元在高光谱图像中广泛存在，成为制约高光谱技术发展的一个难点。因此研究如何有效地进行端元提取具有重要的意义。基于线性混合模型（Linear Mixing Model，LMM）的端元提取算法最为丰富[1]。过去几十年中大量端元提取算法相继被提出，其中比较流行的算法有纯净像元指数（Pixel Purity Index，PPI）[2]、顶点成分分析（Vertex Content Analysis，VCA）[3]、最小体积约束的非负矩阵因数分解算法（Minimum Volume Constraint Nonnegative Matrix Factorization，MVC-NMF）[4]等。上述算法均是在线性光谱混合模型的基础上建立，仅仅满足单形体结构分布的像元，没有考虑残存误差的影响，因此上述算法在高光谱影像中提取的端元与真实端元有一定的差距。

近年来粒子群算法在许多领域被广泛应用，Omran等人[5]将粒子群优化算法（Particle Swarm Optimization，PSO）引入端元提取中，解除了端元提取中仅依赖单形体结构的局限。张兵等人[6]提出了离散粒子群优化（Discrete Particle Swarm Optimization，D-PSO）算法并具有良好的端元提取效果，但算法对粒子的初始位置差，收敛速度较慢。陈伟等人[7]以纯净像元指数（PPI）较高的像元作为预选像元，有效地提高了算法的效率，在估计端元光谱的效果良好。杨可明等人[8]将混沌机制引入到粒子群中以实现端元提取。吴国伟等人[9]将蛙跳分组思想引入D-PSO算法中，增强了粒子群的搜索能力。杨斌等人[10]使用顶点成分分析（VCA）算法求得的端元作为引导粒子，有效地加速粒子群收敛。以上算法在提取端元时，忽略了破碎零散的真实高光谱影像作为粒子群的搜索空间对端元提取结果的影响，导致算法的精度丢失。

本文提出一种基于粒子群搜索空间优化的体积约束误差最小化算法，针对粒子群的搜索空间进行改进，使用混合光谱相似性测度（SID_SA）对PPI较高像元光谱特征进行排序，优化粒子群的初始位置以及搜索空间，优化搜索空间使粒子搜索时搜索空间更加平滑。在演化过程中结合粒子的信息，对粒子的参数自适应调整，在缩小原始图像与反演图像的误差的同时对体积进行约束，在搜索端元的同时保持其原有的形状，使提取的结果更接近真实端元，提高了端元提取的精度。

1 算法与模型

1.1 粒子群优化算法

粒子群优化算法（PSO）[11]是由Eberhart和Kennedy开发的一种新的进化算法，它最早源于对鸟类觅食行为的观察研究，由于其参数少、具有较好的鲁棒性，很快被应用于多目标探测、信号处理等领域。在PSO中，每个寻优问题的潜在解都可以想象成D维搜索空间上的一个“粒子”（Particle），每个粒子根据自身信息和群体信息不断地更新它们各自的速度、飞翔的方向和距离，最终得到全局最优解。

粒子群算法是一种进化算法。假设在D维的搜索空间中，粒子群的个数是N，第i(i=1,2,…,N)个粒子所处的位置是Pi=[Pi1,Pi2,…,PiD]，飞行速度是Vi=[Vi1,Vi2,…,ViD]。第k次迭代时粒子记录的自身历史最优解为 pbest，粒子群的最优位置为gbest，每个粒子通过式（1）、式（2）不断更新各自的速度和位置。

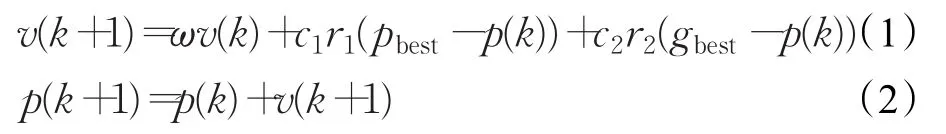
上式中，k为当前迭代次数，ω为速度惯性权重，一般取ω=0.8，c1、c2为学习因子，一般取 c1=c2=2，r1，r2是介于[0，1]内的随机数。

1.2 线性混合模型

高光谱影像端元提取是在影像中提取或估计出混合像元中“纯”地物的光谱。这类“纯”地物称为端元。端元提取可以看作是一个组合优化问题，其约束条件一般为高维空间中单形体体积或混合光谱分解后的误差最小。

端元所占混合像元的百分比，即为端元的丰度。可表示为：

式中，X和x分别表示b×N的影像和b维的像元光谱矢量。b是影像的波段维数，N是影像的像元数。A和ai分别表示b×p的端元矩阵和第i个b维的端元矢量，p是端元数。si是像元x中端元ai的丰度值，S是p×N的丰度矩阵。E和ε分别表示误差矢量和误差矩阵。基于丰度的实际物理意义，丰度矩阵S必须满足两个约束条件，即非负约束与和为1约束的全约束条件。

当E和ε越小，表示提取的端元反演生成的图像与原图像越接近，端元提取效果越好。

2 基于粒子群搜索空间优化的端元提取

本文基于PSO算法原理，在线性混合模型的基础上，以体积钳制下解混误差最小为目标，提出一种基于粒子群优化算法的高光谱影像端元提取算法（PSO-VCEE），下面是对本文算法的具体描述。

2.1 粒子群搜索空间优化

粒子群算法是一种应用于连续空间的、具有较好的全局搜索能力和寻优速度的群体智能优化算法[12]。为提高粒子群算法的搜索能力和优化效率并避免陷入局部最优，本文将混合光谱相似性测度排序法融合到粒子群算法中，针对高光谱真实影像中的零散搜索空间提出一种零散空间聚类排序为连续空间的优化算法。

传统的排序算法应用与高光谱数据仍然存在明显的局限性，难以取得理想的结果，本文结合光谱信息量（SID）和光谱角（SAM）提出混合光谱相似性测度（SID_SA）作为光谱排序的指标[13]。SID_SA综合考虑了光谱曲线形状与光谱信息量，在进行光谱相似性分析时具有较强的光谱判别能力。

混合光谱相似性测度可表示为：

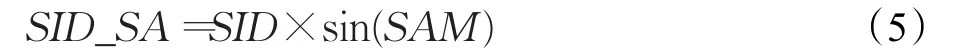
SID通过相对熵（KL）距离计算两个地物光谱间的相对熵，即信息量的差异：

rj和ri为两个不同的光谱，D(ri||rj)和D(rj||ri)分别是ri和rj的相对熵与rj和ri的相对熵。

SAM通过计算两个地物光谱间的夹角来区分类别，即光谱角：

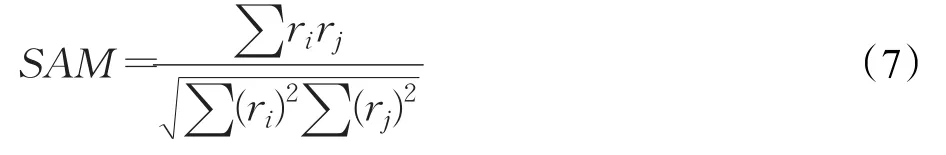
混合光谱相似性测度排序法的基本思想是：将高光谱影像中的预选像元与不同的随机光谱反复计算SID_SA值，预选像元中相似的光谱与同一随机光谱的SID_SA值总是较为接近。本文排序算法选取随机生成的100个光谱与预选像元进行SID_SA值计算。每个预选像元对所计算得到的SID_SA值进行叠加，最终使用叠加后的SID_SA值作为依据，对预选像元进行排序。

2.2 粒子编码

本文的粒子采用实数编码的方式，每个粒子所在的位置为 p个b维向量的序列号，每个序列号表示一个b维的端元光谱向量。每个粒子的p个位置有各自的速度。也就是说每个粒子的p个位置集合都是一个高光谱影像端元提取的可行解。粒子的位置和速度结构如下：

2.3 适应度函数

通过以下公式计算每个粒子的适度值：

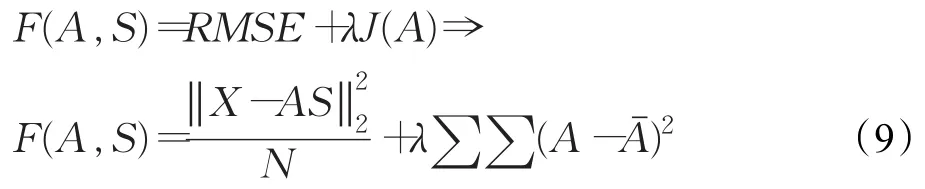
约束为

该适应度函数主要是求两个部分最小化的问题，其中第一部分均方根误差（RMSE）为原始影像与反演影像的相似程度，误差越小说明所提取的端元集合A质量越好。另一个部分J(A)为体积最小化约束，体积的定义用每个端元到单形体中心的欧氏距离表示。仅仅依赖影像分解后误差最小化作为评判标准可能会导致得到的端元光谱与真实端元光谱出现较大偏差。J(A)对端元集合构成的单形体体积进行最小化约束，抑制一些位于单形体边缘的噪点，对提取结果产生影响。

λ为惩罚系数。λ控制着适应度计算过程中“解混误差”和“体积约束”的相对贡献量。λ取值的大小受到多个参数影响，例如影像的灰度值大小、影像的维数、端元的个数等。实验表明通常使体积约束与平均误差相差一至两个数量级时效果较好。λ的取值接近于0，本实验取为0.000 5。

2.4 粒子群的参数设置

ω、c1、c2以及位置钳制是PSO-VCEE的重要参数，其数值设置得是否合适对粒子群的收敛速度与最优结果存在很大影响。

2.4.1 自适应惯性权重ω

惯性权重在最初的粒子群算法中通常取常数0.8，2009年Engelbrecht提出随着算法迭代的进行，ω需要逐渐减小的思想[14]。在算法开始阶段，取较大的ω值可以使算法不容易陷入局部最优，到算法的后期，取较小的ω值可以使收敛速度加快，使收敛更加平稳，不至于出现在最优位置的“振荡”现象。常用的递减策略为：

其中，ωmax=0.95，ωmin=0.4，t为当前迭代次数，tmax为最大迭代次数。

相对于使用迭代的次数选取ω，将当前粒子位置与全局最优位置的距离作为ω的递减策略变量显得更为合理。相对全局最优位置距离较大的粒子，取较大的ω值可以使算法不容易陷入局部最优，具备更强的探索能力。相对全局最优位置距离较小的粒子，取较小的ω值可以使粒子收敛更加平稳。

其中Pi为粒子位置编码，Pbest为全局最优位置，Distmax为迭代过程中粒子间距离的历史最大值。本文中ωmax取值0.95，ωmin取值0.4。

2.4.2 学习因子

c1为自身学习因子，表示粒子经历过的历史最优位置对粒子行动的影响权重；c2为社会学习因子，表示粒子群体最优位置对粒子行动的影响权重。本文中c1=c2=2。

2.4.3 位置钳制

由于端元分布在单形体的顶点上，为了去除影像中混合像元的干扰，算法可以对粒子的位置进行限制，使其在有意义的范围内进行搜索，加速算法的效率。纯净像元指数（PPI）在位置钳制中可以作为一个有效的指标，迭代过程中使用纯净像元指数大的像元作为粒子的搜索空间。本文中对于模拟影像和真实影像使用纯净像元指数前20和100的像元作为预选像元。

2.4.4 光谱钳制

在计算粒子适应度时，对每个粒子中的端元集合中不同的两个端元进行光谱角（SAM）角度计算，当SAM小于一定的阈值T时，则认为两个端元相似，适应度函数直接跳过复杂的计算步骤，返回默认的极大值Fmax。光谱钳制可以有效防止粒子群在迭代过程中，存在两个相似光谱的粒子带入适应度函数的矩阵运算，导致Matlab中矩阵接近奇异值，影响结果的准确性，产生无效解的情况。T值和Fmax值通常受到多个参数影响，例如影像的灰度值大小、影像的维数等。本文中T取5，Fmax取100。

2.5 算法流程

基于粒子群优化算法的高光谱影像端元提取算法可以划分为两个阶段：

在基于粒子群优化算法的高光谱影像端元提取算法的准备阶段，首先用PPI算法对原始影像进行处理，保留PPI指数大的像元作为预选像元参与计算。然后针对预选像元使用光谱相似性测度（SID_SA）进行排序，优化粒子群搜索空间，得到排序后的像元解集。

在端元提取算法粒子群的计算阶段，根据光谱钳制，先对每个粒子进行判断是否是一个可行解，如果粒子的端元集合中存在相似光谱，则跳过后面复杂的计算，返回极大值Fmax=100。在粒子群迭代移动的过程中，根据每个粒子距最优解的距离和迭代的次数，自适应地调整系数，使算法在加速收敛速度的同时保持良好的搜索能力。最后反复迭代直到满足结束条件（误差值小于阈值60，粒子每个维度上最大值与最小值收敛距离小于20或达到最大迭代次数500，输出结果）。算法流程如图1所示。

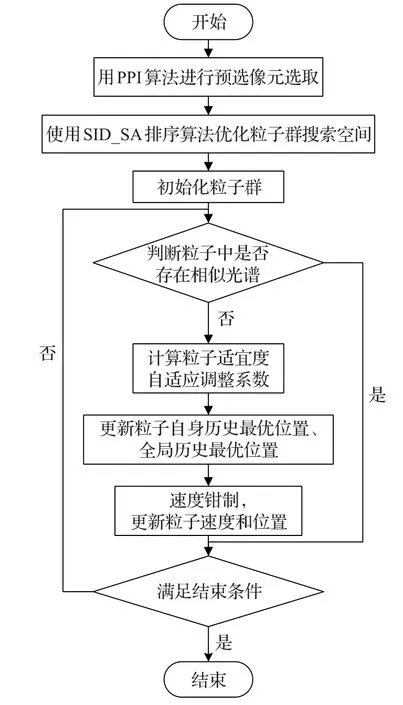
图1 算法流程图

3 实验分析

为了验证本文算法的性能，本章分别采用模拟数据和真实数据对算法进行验证，算法由MatlabR2014a编程实现。计算机配置为：计算机操作系统为Windows 7旗舰版 32位SP1，处理器为Intel®Core™i5-3570，主频3.40 Hz，内存为DDR3-4 GB（3.47 GB可用）。

3.1 模拟数据实验

3.1.1 评价指标

模拟实验使用4个评价因子来评价算法端元提取的性能，首先，利用3个评价因子来评价实验提取端元re与标准端元rs的相似性，3个评价因子的数值越小，则表示提取端元re与标准端元rs越相似。

（1）光谱信息量(SID)

D(re||rs)和D(rs||re)分别是re和rs的相对熵与rs和re的相对熵。

（2）光谱角(SAM)

（3）欧式距离(ED)

式中b为图像的波段数。

其次，用均方根误差(RMSE)来评估提取端元反演图像与模拟图像的相似度，RMSE值越小，相似度越高。

式中X为原图像，A为端元矩阵，S为丰度矩阵，N为图像中像元的数量。

3.1.2 算法性能分析

为了验证本文算法的性能，本文选择光谱范围0.38～2.5 μm波长区间内波段b=166的数据进行分析，利用USGS数字光谱数据库中的3个纯净光谱构建混合像元个数n=100的模拟图像，图像中存在的三种端元分别为明矾石、铵长石和白云母，其中明矾石、铵长石在模拟数据中存在对应的纯净像元，白云母不存在纯净像元，混合像元中白云母最高含量不超过80%。最后，向模拟数据中加入信噪比为20 dB的高斯噪声来模拟影像的误差与噪声，并将本文的实验结果分别与VCA、MVC-NMF、D-PSO算法针对同一模拟数据取得的结果进行比较。

表1以混合像元中含量不超过80%的白云母为例，将不同算法提取的白云母光谱与标准端元光谱进行对比。可以看出，在3个评价因子中PSO-VCEE的数值都优于其他三种端元提取算法，PSO-VCEE提取缺失的白云母光谱更优。

取5次实验的均值作为量化的结果，四种算法所提取的端元光谱曲线（不包括噪声）如图2（b）～（e）所示。可以看出，针对同一数据的提取结果PSO-VCEE所提取的光谱曲线明显优于其他算法，与标准光谱更为匹配。

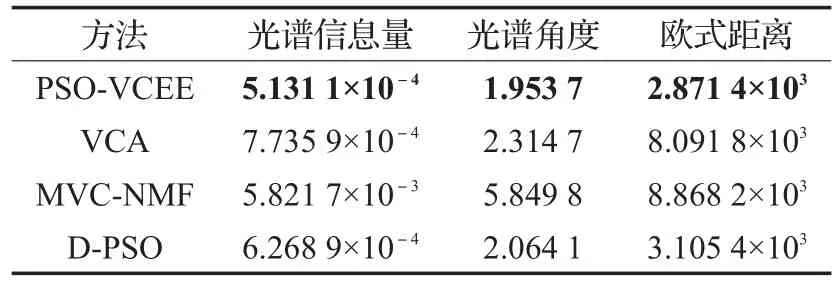
表1 模拟数据中四种方法提取的白云母与标准光谱相似性对比

最后，将PSO-VCEE、VCA、MVC-NMF和D-PSO方法提取到的端元对模拟图像进行反演，反演后的图像与原图像的平均误差（RMSE）如表2所示。PSO-VCEE算法所反演的图像与模拟图像更为接近，效果更好。

表2 模拟图像与四种方法反演图像均方根误差对比

3.1.3 不同端元数的效果评价

为了检测算法对含不同端元数模拟图像的端元提取能力。向原有的模拟图像加入不同的端元光谱（榍石、蒙脱石、高岭石、镁铝榴石、皂石和玉髓），形成端元数量分别为3、5、7、9的模拟图像，加入信噪比为20 dB的高斯噪声来模拟影像的误差与噪声，并将本文算法提取的白云母端元分别与VCA、MVC-NMF、D-PSO算法取得的结果进行比较。

表3使用SID、SAM和ED三种评价因子来比较四种算法所提取的端元精度，并加粗了各项的最好结果（由于表格大小的限制，SID的数值为表格中的值×10-4，ED的数值为表格中的值×103）。综合三个评价因子得出，PSO-VCEE算法的结果最好，其次是VCA、D-PSO和MVC-NMF算法。四种算法随着端元数量的增加精度都有所降低，对于欧氏距离ED与光谱角SAM，PSOVCEE与其余算法对比精度较高，说明体积约束起到了较好的效果，PSO-VCEE所提取的端元更接近标准光谱。通过不同端元数量的模拟数据实验，可以看出PSO-VCEE算法较其余三种算法在端元提取的精度上具有一定的优势，提高了端元光谱的提取精度。

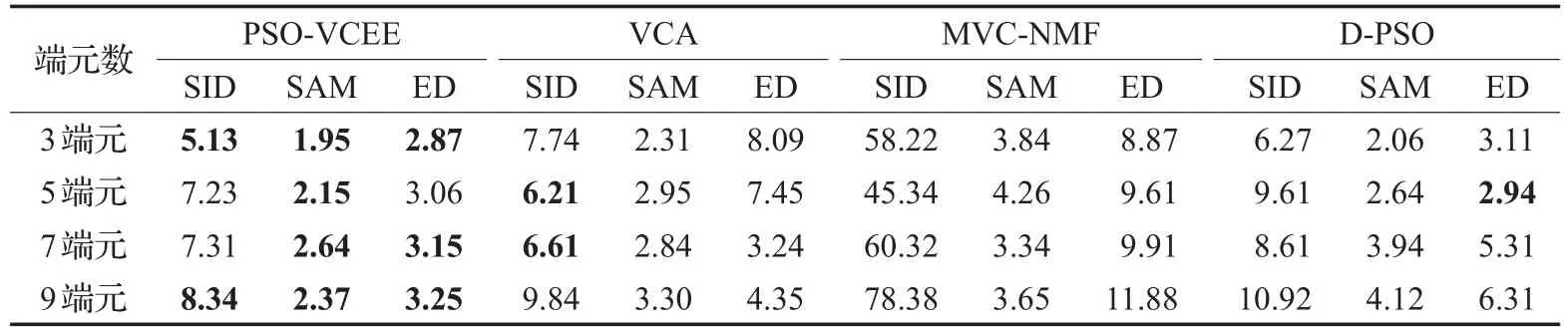
表3 模拟数据中四种方法提取的白云母与标准光谱相似性对比

3.2 真实数据实验

3.2.1 实验数据

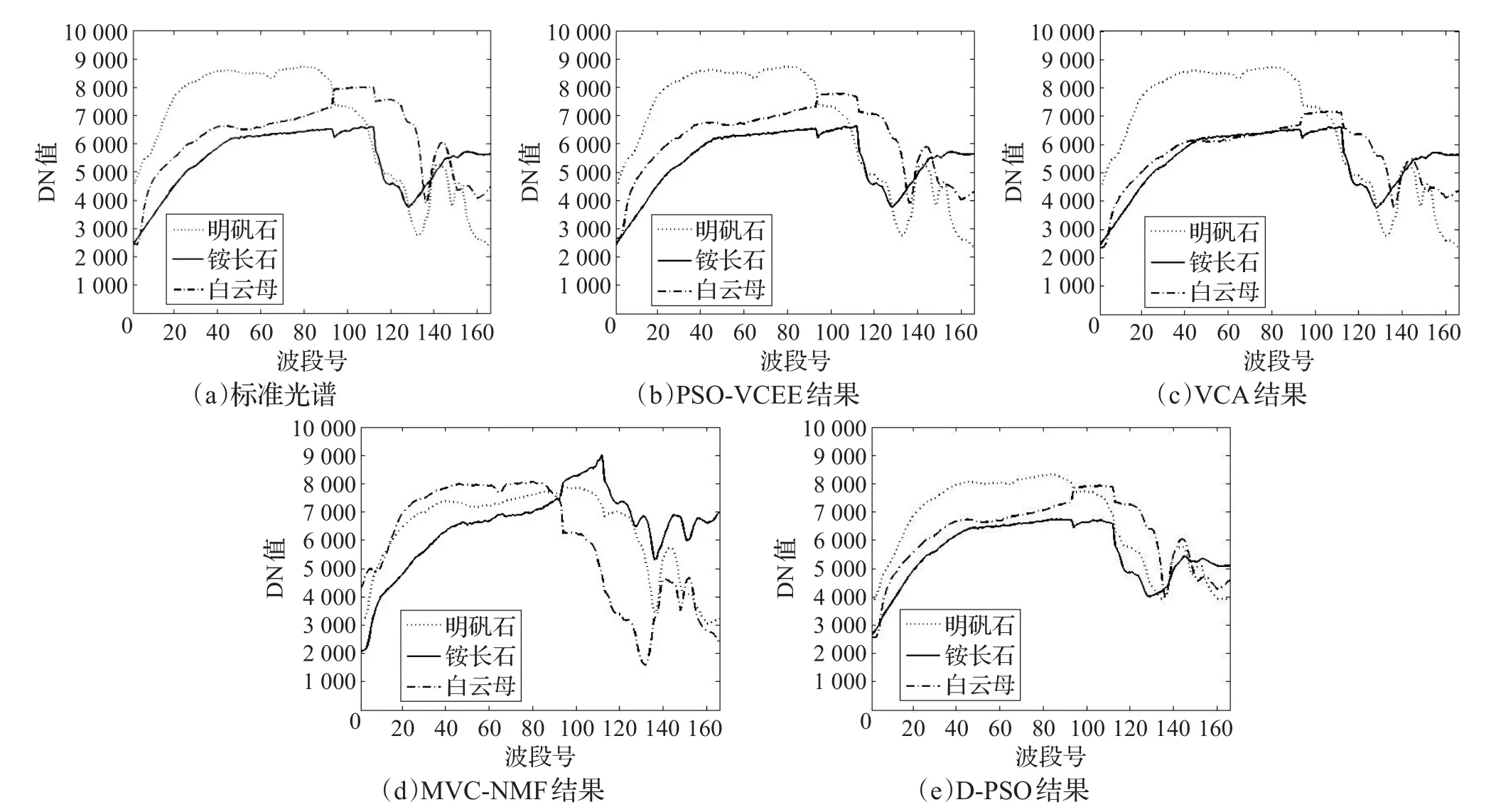
图2 光谱对比图

真实数据实验所采用的数据是从AVIRIS获取的Cuprite矿区高光谱影像，本文选用230像素×240像素的子区域作为实验数据。AVIRIS在0.38～2.5 μm的波长区间内共有224个波段，去除水汽吸收严重、低噪声比和质量较差的波段（1～6，98～113，117～120，148～167，221～224）之后，剩下总共166个波段。如图3所示。

图3 AVIRIS，Cuprite矿区高光谱子区域影像波长0.657 8 μm

采用虚拟维度算法（VD）[15]并结合该地区过去的相关调查实验成果[16]确定图像中端元个数为10，即p=10。通过提取的端元光谱与对应矿物光谱库进行比对，找到对应端元光谱的类别，确定了榍石、铵长石、蒙脱石、高岭石、明矾石、镁铝榴石、高岭石#2、白云母、皂石、玉髓10种物质。

3.2.2 粒子群算法的收敛性能评价

若可行解的搜索空间太大，会影响粒子群算法的效率。因此先使用PPI算法获取100个候选像元，对这100个候选像元进行光谱排序后构成可行解空间。PSOVCEE与D-PSO的参数设置如下：粒子的个数为50个，最大迭代次数500次。每组迭代实验进行10次，通过大量的实验得出RMSE=36.24为最小值，即看作全局最优解，进而比较不同算法在不同迭代次数时全局收敛次数R和局部收敛的次数L，并用所有实验RMSE与时间Time的均值作为实验结果进行对比。

从表4中可以看出当迭代次数到达100次时，由于迭代次数较少，PSO-VCEE与D-PSO均未出现全局收敛。随着迭代次数的增加，PSO-VCEE出现全局收敛的次数均大于D-PSO，并且当迭代次数大于200次时，PSO-VCEE基本都达到了全局收敛。而D-PSO出现全局收敛的次数仅占50%～70%。说明PSO-VCEE优化粒子群搜索空间和自适应惯性权重ω起到了良好的效果，收敛的能力更强。

在相同的迭代次数下，PSO-VCEE较D-PSO算法所损耗的时间相对较少，说明PSO-VCEE针对每个粒子的光谱钳制与位置钳制起到了较好的效果，跳过了“劣质”粒子的复杂运算，优化了粒子群的算法效率。

3.2.3 算法精度评价

在实验中将提取的端元与USGS标准波谱库中对应的光谱进行对比来验证算法的有效性。表5为各个算法提取端元与USGS标准波谱库中对应光谱的光谱角对比结果。两条光谱曲线的光谱角越小，则表示光谱越相似，提取效果越好，表中加粗的数字为不同算法对比后最小的光谱角。可以看出，PSO-VCEE提取的结果明显优于其他算法，而且成功提取了MVC-NMF无法找到的镁铝榴石、玉髓端元。与VCA算法的对比，PSOVCEE提取的榍石、铵长石、高岭石、高岭石2、明矾石、镁铝榴石和玉髓端元光谱更优，其余的端元光谱角对比两者接近。与D-PSO算法的对比，蒙脱石、镁铝榴石、玉髓三种物质光谱一致，其余端元提取的结果对比，PSOVCEE均优于D-PSO。总体而言，提取的端元光谱更接近光谱库标准光谱，更具可信度。总体而言，PSO-VCEE具有较高的端元提取精度。

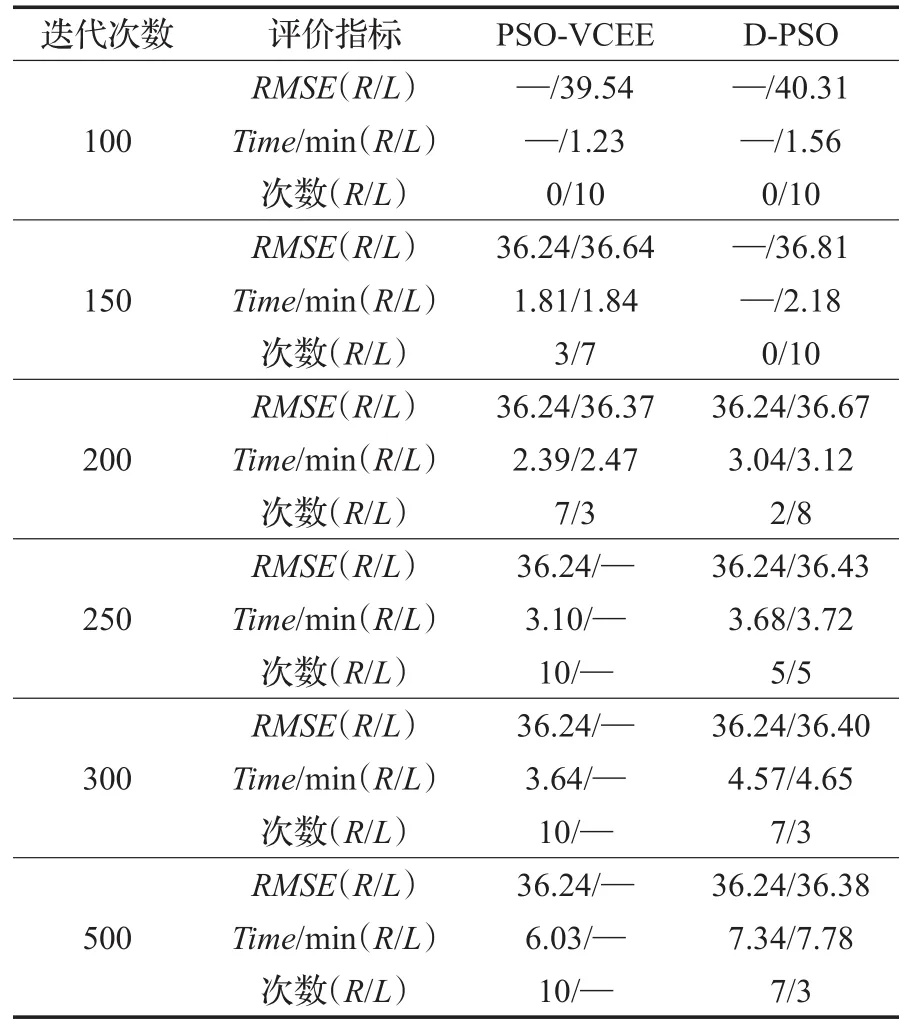
表4 不同迭代次数下两种粒子群算法收敛结果的对比

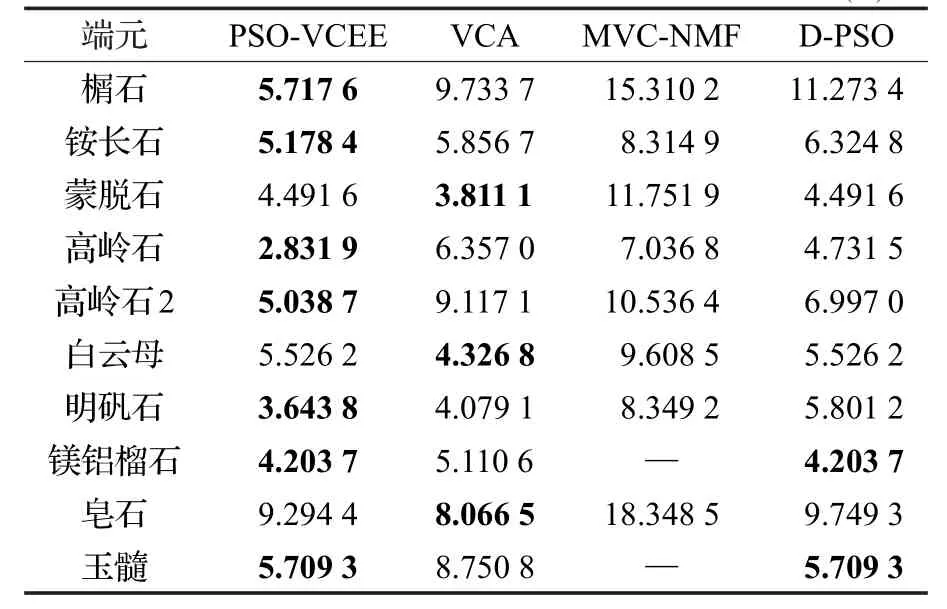
表5 AVIRIS提取端元的光谱角比较 （°）

各种算法提取结果的反演图像与原始图像的误差如表6所示。可以看出，PSO-VCEE、D-PSO求得的反演图像相比VCA与NMF算法，均方根误差(RMSE)更小。

由PSO-VCEE、VCA、MVC-NMF和D-PSO所得端元的丰度图如图4所示。从图像质量上分析，MVC-NMF算法的丰度图像中存在噪点较多，效果较差，玉髓与镁铝榴石丰度图中与其他三种方法丰度图相比相差较大，说明MVC-NMF不能有效地提取玉髓与镁铝榴石两种端元。从图像的亮度上看，D-PSO的丰度图亮度较大，表示图像中大部分像元纯净度较高，图像中明暗过渡差，与高光谱影像存在大量的混合像元的客观规律不符。与MVC-NMF和D-PSO相比，PSO-VCEE、VCA矿物分布更接近真实值。综合图4看来，PSO-VCEE能较好地反映真实矿物的分布情况。

表6 AVIRIS图像与四种方法反演图像均方根误差对比

4 小结

本文以线性混合模型为基础，在图像误差最小化的前提下结合体积钳制思想，提出了一种基于粒子群优化的端元提取算法（PSO-VCEE）。粒子群算法在参数优化领域取得了良好的效果，其搜索空间是连续的，本文将粒子群优化算法应用到端元提取中，针对高光谱图像中维数高、端元分布零散问题，使用混合光谱相似性测度对预选像元进行光谱聚类排序，优化了粒子群的搜索空间。在模拟数据和真实数据中，通过与VCA、MVCNMF、D-PSO端元提取算法对比，证明PSO-VCEE算法提取的端元结果更接近标准的端元光谱。

图4 丰度反演图

PSO-VCEE、VCA、MVC-NMF以及D-PSO端元提取算法运用于真实图像所消耗的时间分别为190.47 s，1.03 s，66.38 s，285.13 s。PSO-VCEE算法相比于D-PSO算法，消耗的时间明显降低，但是与传统的端元提取算法VCA对比，算法的效率仍然有待提高。粒子群算法的运算过程中，粒子间相对独立，研究PSO-VCEE算法的并行化实现方法，有望于提高算法效率，后续研究也将从这方面展开。

参考文献：

[1]Keshava N，Mustard J F.Spectral unmixing[J].Signal Processing Magazine，2002，19（1）：44-57.

[2]Boardman J W，Kruscl F A，Grccn R O.Mapping target signatures via partial unmixing of AVIRIS data[C]//Fifth Jpl Airborne Earth Science Workshop，1995：23-26.

[3]Nascimento J M P，Dias J M B.Vertex component analysis：A fast algorithm to unmix hyperspectral data[J].IEEE Transactions on Geoscience&Remote Sensing，2005，43（4）：898-910.

[4]Miao Lidan，Qi Hailong.Endmember extraction from highly mixed data using minimum volume constrained nonnegative matrix factorization[J].IEEE Transactions on Geoscience&Remote Sensing，2007，45（3）：765-777.

[5]Omran M，Engelbrecht A P，Salman A.Particle swarm optimization method for image clustering[J].International Journal of Pattern Recognition&Artificial Intelligence，2005，19（3）：297-321.

[6]张兵，孙旭，杨丽娜，等.一种基于离散粒子群优化算法的高光谱图像端元提取方法[J].光谱学与光谱分析，2011，31（9）：2455-2461.

[7]陈伟，余旭初，张鹏强，等.基于粒子群优化的高光谱影像端元提取算法[J].计算机工程与应用，2012，48（8）：189-193.

[8]杨可明，张涛，刘士文，等.混沌离散粒子群优化的高光谱影像端元提取算法[J].测绘科学技术学报，2014，31（2）：148-156.

[9]吴国伟，赵艳玲，王龙，等.基于蛙跳算法的离散粒子群优化端元提取[J].中国图象图形学报，2015，20（5）：724-732.

[10]杨斌，罗文斐.约束非负矩阵分解框架下高维自适应粒子群端元提取[J].遥感学报，2015，19（2）：240-253.

[11]Eberhart R，Kennedy J.A new optimizer using particle swarm theory[C]//International Symposium on MICRO Machine and Human Science，1995：39-43.

[12]王经卓，樊纪山.空间数据关联的多目标粒子群优化算法[J].控制与决策，2015（7）：1291-1297.

[13]张浚哲，朱文泉，董燕生，等.一种基于变权重组合的光谱相似性测度[J].测绘学报，2013，42（3）：418-424.

[14]Engelbrecht A P.计算群体智能基础[M].北京：清华大学出版社，2009.

[15]Chang C，Du Q.Estimation of number of spectrally distinct signal sources in hyperspectral imagery[J].IEEE Transactions on Geoscience and Remote Sensing，2004，42（3）：608-619.

[16]Swayze G A.The hydrothermal and structural history of the Cuprite mining district，southwestern Nevada：An integrated geological and geophysical approach[D].University of Colorado Boulder，1997.