基于同态滤波的水下图像增强与色彩校正模型

王永鑫，刁 鸣，韩 闯

WANG Yongxin1，2,DIAO Ming1,HAN Chuang2

1.哈尔滨工程大学 信息与通信工程学院，哈尔滨 150001

2.哈尔滨理工大学 测控技术与仪器黑龙江省高校重点实验室，哈尔滨 150080

1.College of Information and Communication Engineering,Harbin Engineering University,Harbin 150001,China

2.The Higher Educational Key Laboratory for Measuring&Control Technology and Instrumentations of Heilongjiang Province,Harbin University of Science and Technology,Harbin 150080,China

1 引言

高质量的水下图像是人类开发海洋资源，探索水下生态环境，进行海洋工程的基本要素[1]。光信号的衰减作用是制约水下图像质量的主要因素。水体对于分属三个不同波长区间的三基色信号的衰减幅度不一致，例如红色通道在水下的衰减程度远大于蓝、绿通道，因此水下图像的色彩偏重于蓝绿色。这一现象易造成水下图像色彩失真，对比度下降，细节不清晰等问题[2-3]。

针对这一问题，近年来国内外学者提出了一些有效的图像增强方法用于改善水下图像的图像质量。Chiang等[4]通过雾天图像成像模型对水下图像成像进行建模，再估计出目标与观测者之间的距离图。根据成像模型和距离图，对水下图像进行人造光补偿，进而提高水下图像的可视化效果。杨爱萍等[5]提出一种水下复原方法用于克服水下图像颜色衰减与雾化效果。该方法首先根据暗通道先验的方式分别对三个色彩通道进行色彩校正，再根据散射作用与光线波长的关系对透射率进行估计，继而修复了水下图像的色彩偏差并抑制了水体对于背景光的散射作用。Borker等[6]将水下图像增强看作是两个子图的融合过程。首先，通过对水下图像进行对比度拉伸，从而生成抑制雾化效果的子图1。其次，对三个颜色通道进行自适应直方图均衡化方法，从而生成颜色恒定的子图2。最后，通过对子图1和子图2进行基于PCA的图像融合方法，进而合成色彩不失真、细节清晰的水下图像。Galdran等[7]提出一种自动R通道水下图像恢复方法。该方法分为三个步骤：根据R通道的亮度，对水下场景的背景光进行估计；在已知背景光的前提下，对各像素的透射比进行估计；根据对水下成像模型进行逆变换，结合已估计的背景光和透射比对未衰减的目标亮度进行校正。实验结果验证了该算法对校正色偏，水下图像去模糊均有较好的效果。

虽然上述方法对于水下图像的视觉效果具有一定的改善作用，但是图像的细节、清晰度、色彩恒定性仍有待进一步提高。为了改善水下图像不清晰以及色彩失真问题，本文提出一种基于同态滤波的水下图像增强与色彩校正模型。该模型通过比尔-朗伯定律以及路径辐射分量建立未衰减前目标亮度与衰减后目标亮度之间的对应关系。通过剩余能量比估计出水体对于三基色通道亮度的衰减程度。通过同态滤波抑制由目标与观测值之间的距离分量所引起的图像雾化效果。对水下成像模型进行级数展开，在不给出目标与观测者之间的距离的前提下，推导出一种有效的水下图像色彩校正模型。实验部分从主、客观两方面验证了本文的有效性。

2 本文算法

2.1 水下成像模型

水下成像模型主要由两部分组成[8]。第一部分是正透射作用，即水体对于目标亮度的衰减作用。正透射对于光线的衰减作用可以由比尔-朗伯定律[9]来构造。第二部分是路径辐射，即由环境光所引起的后向散射作用[10]。因此水下成像模型可以表示为：

其中x代表像素的空间位置，λ代表不同颜色通道，J表示未经过衰减的目标亮度值，I表示经过正透射和路径辐射目标的亮度值，Aλ表示环境光的亮度值，t表示透射比。

根据比尔-朗伯定律透射比可以表示为：

其中β表示介质的消光系数，d代表目标与观测者的直线距离，N表示标准化剩余能量比。将式（2）带入式（1）中得到如式（3）所示的更新后的水下成像模型。

Chiang等[4]对于多种类型的水体进行实验，总结出标准化后的剩余能量比应满足如式（4）所示的关系：

由式（4）可知，水体对于波长较长的红色光信号衰减程度较大，对于波长较短的绿色和蓝色信号衰减程度较小。根据文献[4]可知，环境光的亮度值可以表示为：

其中Ω(x)表示以坐标x为中心的局部方形区域。本文选用5×5的局部方形区域用于估计环境光的亮度值。

2.2 基于同态滤波的水下图像亮度估计方法

根据2.1节的论述可知，如式（3）所示的水下成像模型中只有目标与观测者之间的直线距离d未知。由于距离信号d是变化缓慢的低频信号[11]，因此本文通过滤波的思想将距离信号过滤掉。根据公式（3）可知，距离信号位于指数部分，因此首先需要通过同态滤波提取距离信号。对公式（3）进行整理得到如式（6）所示的等式：

对公式（6）等号两边分别进行指数运算得到如式（7）所示的等式：

由于目标亮度Jλ属于频率变化较快的高频信号，而距离d属于低频信号，对公式（7）进行低通滤波得到水下图像低频分量（即ln(Nλ)×d(x)），再用水下图像减去这一低频分量就能得到不受距离影响的目标亮度分量。这一过程如式（8）所示。

其中LPF表示低通滤波。对公式（8）进行整理，得到如式（9）所示的 Jλ计算方法。

2.3 色彩恒定模型

由于公式（9）是一个关于Iλ的非线性方程，因此如果分别对红、绿、蓝三通道进行如式（9）所示的图像增强方法，则会产生偏色现象进而导致影响图像的色彩恒定性。为了保持色彩的恒定性，本文提出一种水下图像色彩恒定模型。该模型的推导过程如下：

首先，对公式（3）进行整理得到如式（10）所示的形式。

令 f是关于d(x)的函数，即。通过一阶麦克劳林级数对 f进行级数展开，得到以下形式：

将公式（11）带入公式（10）中得到如式（12）的表达式：

为了推导方便，这里对公式（12）进行变量替换，即公式（13）成立。

其次，令IΣ(x)和JΣ(x)表示由三原色混合而成的像素 x的亮度值。IΣ(x)和JΣ(x)的表达式如式（14）所示。

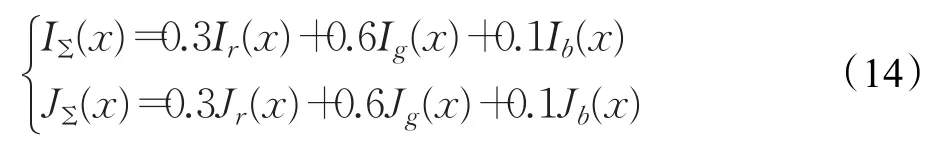
根据公式（14）可知 JΣ(x)由 Jr(x)、Jg(x)、Jb(x)三个变量线性叠加而成，而红、绿、蓝三通道的亮度值均满足如式（12）、式（13）的关系。因此式（15）成立。

对公式（15）进行移项、整理得到任意颜色通道的亮度值，即

其中 ξλ(x)的值由公式（4）、公式（5）所确定，JΣ(x)由2.2节提出的基于同态滤波的水下图像对比度增强方法所确定。求解JΣ(x)的方法如下：根据公式（14）的子方程（1）求解 IΣ(x)；将公式（9）下标 λ用 Σ 替代，将 IΣ(x)带入公式（5）得到 AΣ；将公式（9）下标 λ用 Σ 替代，将IΣ(x)和 AΣ带入公式（9）得到 JΣ。最后将 JΣ和 IΣ(x)带入公式（16）中得到色彩恒定的彩色水下图像。

3 实验结果与分析

实验过程采用CPU i5-7500，内存DDR4-2133，显卡GTX1050作为硬件仿真环境。软件仿真环境是Matlab 2012b，Win 10操作系统。

3.1 水下成像模型参数设置方法

本文所采用的原始水下成像模型（如式（3）所示）中包括一个可以自由选取的参数N（标准化剩余能量比）。尽管Chiang等[4]根据不同的水质将N的范围设定在如式（4）所示的一段比较小的范围内，但是仍然需要根据水体的类型去设定该参数值。这种方式不利于实现算法的通用性。

3.1.1 参数的选取对于图像质量的影响

对公式（3）进行整理，可以得到如式（17）所示的计算未衰减目标亮度Jλ的表达式。

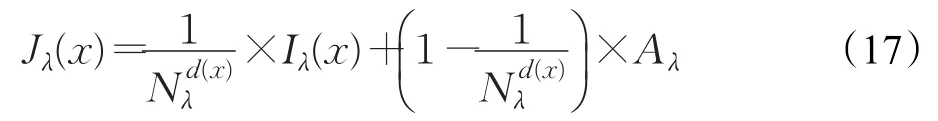
根据公式（17）可知，未经衰减的目标亮度 Iλ(x)由衰减后的目标亮度Iλ和环境光的亮度Aλ两项相加而构成。Iλ的权重系数是1/，Aλ的权重系数是1-1/。

根据公式（17）可知，如果参数的估计值大于N的真值，则Iλ的权重变小，而Aλ的权重变大，因此Jλ的估计值则会更偏向于环境光的亮度值。根据公式（5）可知，全体局部区域像素亮度最小值的最大值决定了环境光的亮度。因此当估计值大于N的真值时，尽管增强图像整体上较为明亮，但是增强图像的对比度下降，继而导致增强图像的清晰度变差。另外，如果参数的估计值小于N的真值，则Iλ的权重变大，而Aλ的权重变小，因此Jλ的估计值则会更偏向于衰减后的目标亮度值。因此当估计值小于N的真值时，增强图像的视觉效果与衰减后的图像相近。

3.1.2 参数设置方法

综上所述，只有当参数的估计值逼近于N的真值时，增强图像的图像质量、清晰度、对比度才能与未衰减的图像保持一致。为了确定合适的参数值，本文利用不同的N值进行实验得到一组增强图像，再从这组增强图像中选出最清晰的图像作为最终的实验结果。实验部分采用的原始水下图像如图1所示。为了验证参数N对于增强水下图像的图像质量的影响，本文对于N值的有效范围(N∈[0,1])进行五十等分，分割后区间的区间端点即为所选取的N值。图2选取了五个具有代表性的N值对应的水下增强图像。

图1 原始水下图像cave和turtle

图2 中每个子图所对应的N值如表1所示。

图2 不同N值对应的实验结果对比

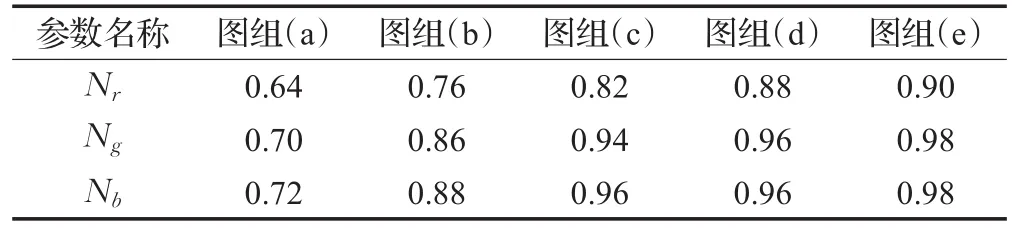
表1 各图组对应的N参数值

从图2可以看出不同子图的模糊度、亮度、明暗对比均不同。例如图像cave的子图（c）的清晰度较高，轮廓纹理较清晰，并且图像的明暗对比效果较佳，因此子图（c）对应的N值更接近于参数N的真实值。子图（a）、（b）对应的阴影部分（两个岩壁以及图像下部的岩石区域）亮度较为昏暗，不利于人眼观察。另外当N值较小时，增强图像整体的视觉效果与如图1（a）所示的原始图像的视觉效果较为接近；子图（c）、（d）的高光区域过于明亮，图像整体的雾化效果较为严重，图像清晰度较差。另外，根据图2可知，不同N值对应的增强图像的主观视觉效果与3.1.1节的理论分析结果保持一致。

由于信息熵主要对图像的细节、清晰度进行评价，图像的信息熵越大，则增强图像清晰度和图像细节就越好，反之亦然。因此本文采用信息熵作为衡量图像模糊化程度的测度，信息熵最高的图像就是最终图像增强结果。图2各子图的信息熵如表2所示。

表2 各子图对应的信息熵

由表2可知图像cave的子图（c）以及图像turtle的子图（c）的信息熵最高。因此这两幅子图像为最终的图像增强结果。

3.2 实验结果对比

对比算法包括：Chiang算法[4]、Borker算法[6]、Galdran算法[7]，以及本文算法。其中本文算法采用上文所述的方法自适应地决定参数N的值。图3是需要增强的名为rock和aquatic的水下图像。

图3 原始水下图像rock和aquatic

由图3（a）可知，原始图像的亮度较低，图像两侧岩石表面的图像细节难以辨识。由图3（a）可知，原始图像的颜色饱满程度较低，图像整体的色调较为暗淡，低照度的阴影部分严重降低了图像质量。图4、图5分别是如图3所示的原始水下图像对应的图像增强结果。

图4 水下图像rock的主观结果对比

由图4可知：Chiang算法在一定程度上提升了图像的照度，但是图像左右两侧岩石部分的亮度差异过大，导致人眼无法分辨右侧岩石部分的图像细节。Borker算法对应的增强图像整体亮度得到一定提升，但是图像的清晰度不高，图像的细节较为模糊不清；Galdran算法对应的增强图像的对比度优于Borker算法，高照度区域的图像层次、纹理适于人眼的主观观察，但是低照度区域（例如图像4（c）右侧岩石部分）的亮度较低主观视觉效果较差。相比而言，本文算法对应的增强图像的亮度较高，图像的纹理、细节较为突出，图像的整体层次感较好。

从图像的亮度和对比度的角度上来说，图5的主观效果与图4基本保持一致，即本文算法对应的增强图像的层次感和细节表现力较强。从图像的色彩方面来看，本文算法的色彩丰富、逼真，图像的整体颜色表现力好于另三种算法。

图5 水下图像aquatic的主观结果对比

表3和表4分别是衡量图像质量的客观评价指标。色阶映射图像质量评价系数（Tone Mapped Image Quality Index，TMQI）[12]是衡量增强图像的色彩与原始图像色彩一致性的指标。TMQI源于Wang等[13]提出的图像结构相似度指标（Structural Similarity Index Measure，SSIM）。TMQI改进了SSIM只能用于无色图像这一缺点，将改进后的SSIM值分别用于测量红、绿、蓝三通道的相似程度。TMQI的值越大，则色彩的一致性越好，反之亦然。TMQI-R，TMQI-G，TMQI-B分别代表红、绿、蓝三通道的色彩恒定性评价系数。

表3 图像rock的客观评价指标

表4 图像aquatic的客观评价指标

由表3、表4可知本文算法对应的信息熵和三个颜色通道对应的TMQI指标均高于另外三种对比算法。因此本文算法对应的图像细节、色彩恒定性优于另外三种相关算法。

4 结束语

为了提高水下图像的图像质量，本文提出一种基于同态滤波的图像增强与色彩恒定模型。本文在由比尔-朗伯定律和路径辐射分量建立的水下光线衰减模型的基础上，通过同态滤波克服了由具有低频性质的距离分量引起的图像模糊效果。通过麦克劳林级数对该模型进行级数展开，推导出一种水下图像色彩恒定模型。实验部分通过主观对比与客观评价两方面，验证了本文方法能够有效地提高水下图像的图像质量，增强图像的对比度、细节、色彩都得到了一定程度的提升。

参考文献：

[1]郭继昌，李重仪，郭春乐，等.水下图像增强和复原方法研究进展[J].中国图象图形学报，2017，22（3）：273-287.

[2]Park D，Han D K，Ko H.Enhancing underwater color images via optical imaging model and non-local means denoising[J].Ieice Transactions on Information&Systems，2017，E100.D（7）：1475-1483.

[3]Tripathi A，Gupta P，Richaria V.Haze removal and color compensation of underwater image and denoising[J].International Journal of Computer Science&Information Technolo，2014.

[4]Chiang J Y，Chen Y C.Underwater image enhancement by wavelength compensation and dehazing[J].IEEE Transactions on Image Processing，2012，21（4）：1756.

[5]杨爱萍，郑佳，王建，等.基于颜色失真去除与暗通道先验的水下图像复原[J].电子与信息学报，2015，37（11）：2541-2547.

[6]Borker S，Bonde S.Contrast enhancement and visibility restoration of underwater optical images using fusion[J].International Journal of Intelligent Engineering&Systems，2017，10（4）：217-225.

[7]Galdran A，Alvarez-Gila A，Alvarez-Gila A.Automatic red-channel underwater image restoration[J].Journal of Visual Communication&Image Representation，2015，26（C）：132-145.

[8]Shwartz S，Namer E，Schechner Y Y.Blind haze separation[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition，2006：1984-1991.

[9]Gordon H R.Can the Lambert-Beer law be applied to the diffuse attenuation coefficient of ocean water?[J].Limnology&Oceanography，1989，34（8）：1389-1409.

[10]Stephan T，Beyerer J.Computergraphical model for underwater image simulation and restoration[C]//Computer Vision for Analysis of Underwater Imagery，2014：73-79.

[11]Petit F，Capellelaize A S，Carre P.Underwater image enhancement by attenuation inversionwith quaternions[C]//IEEE International Conference on Acoustics，Speech and Signal Processing，2009：1177-1180.

[12]Yeganeh H，Wang Z.Objective quality assessment of tonemapped images[J].IEEE Transactions on Image Processing，2013，22（2）.

[13]Wang Z，Bovik A C，Sheikh H R，et al.Image quality assessment：From error visibility to structural similarity[J].IEEE Transactions on Image Processing，2004，13（4）：600-612.