对称传递关系的诱导拓扑及其可数性

孙小义，张贤勇，李 露

SUN Xiaoyi1，2,ZHANG Xianyong1，2,LI Lu1，2

1.四川师范大学 数学与软件科学学院，成都 610066

2.四川师范大学 智能信息与量子信息研究所，成都 610066

1.College of Mathematics and Software Science,Sichuan Normal University,Chengdu 610066,China

2.Institute of Intelligent Information and Quantum Information,Sichuan Normal University,Chengdu 610066,China

1 引言

粗糙集理论[1]是一种处理不精确、不一致、不完整信息与知识的数学工具，也是一种重要的智能信息处理技术。粗糙集理论最初的原型来源于比较简单的信息模型，它的基本思想是通过关系数据库分类归纳形成概念和规则，通过等价关系的分类以及分类对于目标的近似去获得知识发现。目前，该理论已成为人工智能领域中一个较新的学术热点，在机械学习、认知诊断、数据挖掘、知识获取、决策分析等许多领域[2-6]得到了广泛的关注，并应用于医疗卫生、地质环境、机械制造、交通运输等行业[7-10]。

经典粗糙集是在等价关系下定义粗糙近似算子。研究一般二元关系下的粗糙近似算子，比如探讨基于自反、对称、传递的粗糙近似算子，扩宽了对经典粗糙集的适用范围。近年来，许多作者研究了基于新二元关系的广义粗糙集[11-13]。

文献[1]的起源Pawlak粗糙集的上下近似集与拓扑空间中集合的内部与闭包在本质上是相同的，且文献[14]表明：经典粗糙集和以划分为基的拓扑空间是吻合的。由此，粗糙集的拓扑研究具有学术意义[15-16]，粗糙集理论与拓扑的结合得到很多研究[17-18]。文献[19]针对自反传递关系，证明下近似集族组建拓扑，上下近似集即为拓扑闭包与内部。文献[20]针对自反关系θ，证明集族

构成拓扑（其中U为非空有限论域，2U为论域幂集，θ-(X)为下近似集）；当θ自反对称则拓扑（1）还满足（sym）条件，若有拓扑满足（clop）条件则存在自反对称关系θ使得拓扑（1）即为该拓扑；若有拓扑满足（comp）条件，则存在自反传递关系诱使下近似集即为该拓扑内部。文献[21]证明自反传递关系与满足（COMP）紧条件的拓扑具有一一对应，若θ自反传递则拓扑（1）满足（COMP）条件，其中论域不局限于有限性。文献[22]指出，自反传递诱导的拓扑与满足（COMP）条件的拓扑皆是Alexandrov拓扑。文献[23]通过闭包与内部算子研究模糊粗糙集的拓扑结构，证明了自反、传递关系下的近似空间中模糊集的上、下近似算子分别为一个模糊拓扑的闭包、内部算子，且相应的模糊拓扑满足（TC）条件；反之，满足（TC）条件的模糊拓扑的闭包与内部算子也恰为一自反、传递关系下的近似空间中的上、下近似算子。此外，文献[24-25]基于逻辑代数和模糊粗糙来建立粗糙集与拓扑空间的联系，得到许多相应的性质。

综上，粗糙集主要通过二元关系密切联系着拓扑。事实上，二元关系通常涉及自反性、对称性、传递性，该三性关系的层次结构如图1。基于图1，粗糙集一般是由等价关系（即三性）定义粗糙近似算子，但等价关系性质太强；反之，单做一个（自反、对称、传递）关系则性质太弱；所以，双关系探讨是一个可行方向，如上述文献[19，21-23]对自反对称、自反传递具有详细研究。特别地，自反关系比较平凡，不太具有核心性，在性质上弱于对称关系与传递关系。此外，对称传递关系的双性研究罕见文献报道。对此，本文将结合对称性与传递性来研究相关粗糙集近似，其具有完善双性研究的基本动机。具体地，本文主要研究基于对称传递关系的诱导拓扑及其可数性，以进一步揭示粗糙集与拓扑深刻联系。

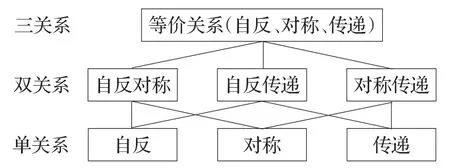
图1 自反、对称、传递三性关系的三层结构

2 粗糙集与拓扑的预备

2.1 粗糙集预备

本节回顾粗糙集的近似集及其性质。有限论域U与二元关系R⊆U×U组建了广义近似空间(U,R)，其中观测集为X,Y⊆U。

定义1[1]X关于R的上下近似集为：

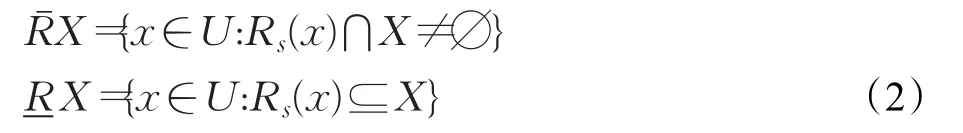
其中为x关于R的后继邻域。相应地，称为上下近似算子。

命题1[1]上下近似集（及算子）具有如下性质：

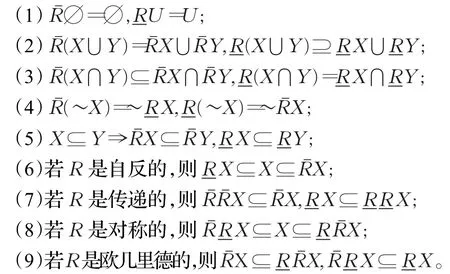
基于二元关系，近似集采用了后继邻域与元素的形式，相关性质聚焦集合运算与二元关系，泛化与弱化了基于等价关系的性质。

2.2 拓扑预备

本节复习拓扑概念与可数性质。

定义2[26]设集族T⊆2U满足开集公理：

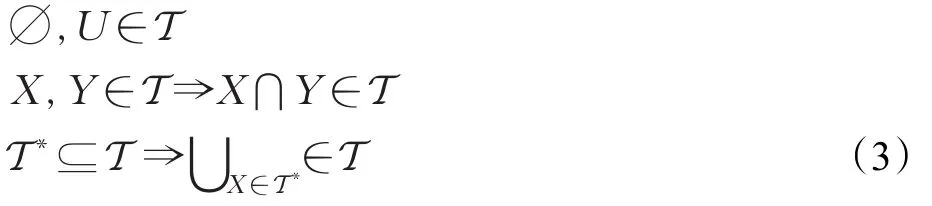
则称T为U上的拓扑，(U,T)为拓扑空间，其中T的每个集元称为开集，开集的补集则为闭集。

定义3[26]设映射i:2U→2U满足内部公理：

则i称为U上的内部算子，其中i(X)称为集合X的内部。类似地，四个条件

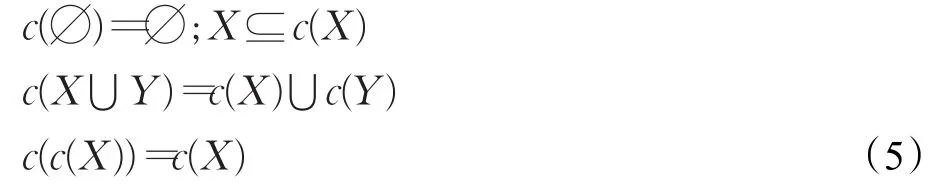
确定的映射c:2U→2U称为U上的闭包算子，其中c(X)称为集合X的闭包。

拓扑是一种包含空集全集且对有限交与无限并封闭的集族结构。其内部与闭包从内外双向界定观测集合，紧密地关联着粗糙集上下近似集的双向逼近[19]。拓扑主要关注在同胚映射下的不变性质，下面介绍可数性拓扑性质。

定义4[26]在拓扑空间(U,T)中，子族B⊆T称为基，若

拓扑空间若具有可数基（即有限个开集组成的基），则称为第二可数。

定义5[26]在拓扑空间(U,T)中，记N(x)为点x∈U的邻域系，子族B(x)⊆N(x)称为x的邻域基，若

拓扑空间满足每点具有可数邻域基，则称为第一可数。

对拓扑可数性，第二可数与第一可数分别由可数基与可数邻域基定义；此外，还可以基于可数稠密子集与可数子开覆盖分别定义可分空间与Lindelof空间。这四种特征均为拓扑性质。下面的结论表明，第二可数蕴含其他可数性，具有基础性。

定理1[26]第二可数拓扑空间性必是第一可数拓扑空间、可分拓扑空间、Lindel of拓扑空间。

在第二可数条件下，四种可数特征均具有对于子空间的遗传性。对乘积空间，第二可数性、第一可数性、可分性均具有可数可乘性，但Lindel of性不具有可乘性。

3 基于对称传递关系的近似集与拓扑

3.1 基于对称传递关系的近似集

本节讨论基于对称传递二元关系的近似集。下面主要采用文献[20-21]的记号风格，以区分2.1节中通常二元关系R及其近似集。具体地，这里设θ为满足对称性与传递性的二元关系，并用θ+与θ-标注上下近似集，而为上下近似算子。

引理1。

定理2X的上下近似集为：

基于定义1与对称传递，引理1提供了单点集{}x的上近似集θ+{x}，其作为核心因素刻画了通常集合的上下近似（定理2）。进而，近似集具有如下基本性质，其深化了命题1所述性质。

命题2关于对称传递关系θ，上下近似集（及算子）具有如下性质：

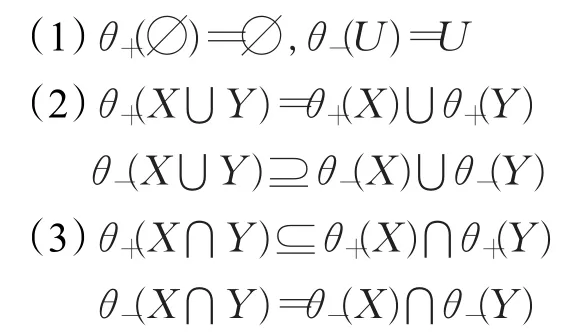
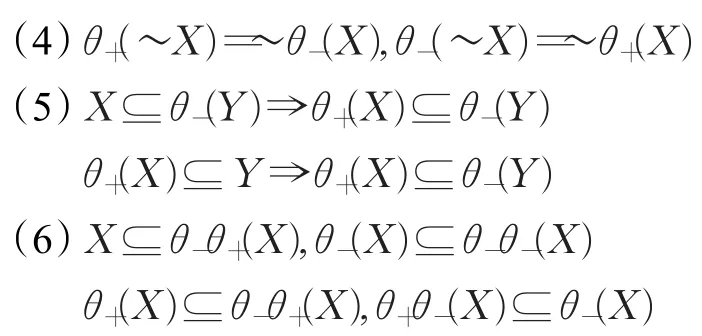
3.2 基于对称传递关系的拓扑

本节利用对称传递关系诱导拓扑，并给出内部与闭包关联于近似集的性质。

定义6定义对称传递关系θ的诱导集族：

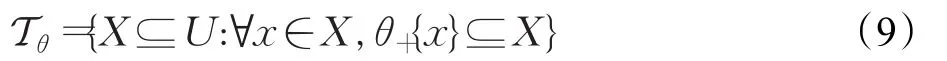
在下述拓扑意义下，Tθ称为θ诱导拓扑。

定理3Tθ是U上的拓扑。

证明（1）∅,U∈Tθ是显然的。

（2）设。 x∈X 且 x∈Y ，故，即

（3）设。因此

综上三条，Tθ成为U上的拓扑。

关于构建思路，对称传递关系θ首先确立单元上近似集θ+{x}（引理1），θ+{x}进而激发拓扑Tθ（定理3）。根据公式（9），其中开集包含它所有元素的单元集上近似。

定理4在拓扑空间(U,Tθ)中，内部算子i与闭包算子c具有如下性质：

其中，孤立点指没有在对称传递关系θ的序对集合里出现的元素。

定理4刻画了Tθ内部与闭包，表明了在对称传递关系下粗糙集与拓扑的关系。诱导拓扑空间(U,Tθ)中的内部与闭包主要分别对应广义近似空间(U,Tθ)的下上近似集；但是，其中存在关于孤立点的描述差异，这主要根源于二元关系θ不一定具有自反性。相应地，内部闭包公式（10）（11）涉及到观测集与孤立点的四种关系。这四种关系其实可以部分界定Tθ开集与闭集，结论如下。

推论1（1）X内含所有孤立点时，θ-(X)为Tθ拓扑开集；

（2）当 X 外含有孤立点 x时，为Tθ拓扑开集；

（3）当X外含所有孤立点时，θ+(X)为Tθ拓扑闭集；

（4）当 X 内含孤立点 x 时为Tθ拓扑闭集。

4 对称传递关系的诱导拓扑的基、邻域基、可数性

4.1 Tθ诱导拓扑的基与邻域基

本节提供诱导拓扑Tθ的基与邻域基，为后续可数性研究奠定基础。

引理2

证明∀y∈θ+{x}有 x∈θs(y)，即(y,x)∈θ。若 ∀z∈θ+{y},则有 y∈θs(z)，即(z,y)∈θ。由 θ传递性，(z,x)∈θ，即 x∈θs(z)。因此，z∈θ+{x}，θ+{y}⊆θ+{x}，进而θ+{x}∈Tθ。

定理5是诱导拓扑Tθ的一个基，且为最小基（即 Bθ⊆B′θ若 B′θ是Tθ的任意基）。

定理6是诱导拓扑Tθ在点x∈U处的一个邻域基，且为最小邻域基（即Bθ(x)⊆B′θ(x)若B′θ(x)是Tθ在点 x 处的任意邻域基）。

证明Bθ是拓扑Tθ的一个基，则对任意x∈U及其任意邻域N(x)，存在x的一个开邻域U(x)使得U(x)⊆N(x)。根据U(x)的开集性与基的定义，Bθ(x)⊆Bθ使得 U(x)=∪B∈Bθ(x)B 。由 x∈∪B∈Bθ(x)B 存在 L(x)∈Bθ(x)⊆Bθ使得因此，Bθ(x)是x的一个邻域基。此外，Bθ(x)的最小基性容易证明。

这里，定理5与定理6利用上近似集构建了诱导拓扑Tθ的基Bθ与邻域基Bθ(x)，它们均具有对应的最小性。

4.2 Tθ诱导拓扑的可数性

利用基与邻域基，本节研究诱导拓扑Tθ的可数性。

定理7拓扑空间(U,Tθ)为第二可数空间、第一可数空间、可分空间、Lindelof空间。

关于诱导拓扑Tθ，基Bθ显然是一个可数族，所以第二可数性存在；邻域基Bθ(x)也是一个可数族，所以第一可数性亦存在。由定理1，利用第二可数性可以直接诱导第一可数性，以及可分性与Lindelof性，即定理7成立。下面对Tθ提供一些基本的可数性刻画。

推论2设 (U′,T ′)为拓扑空间，f:(U,Tθ)→(U′,T ′)。若 f是满的开映射，则(U′,T′)为第二、第一可数空间；若 f是连续映射，则(U′,T′)为可分空间、Lindelof空间。

推论3在(U,Tθ)拓扑空间中，每点 x∈U 具有可数邻域套基{Vn(x)}(n∈Z+)，适合于条件

推论4聚点x∈Xd等价于X-{x}中存在序列收敛于x。

推论5（1）设U′⊆U,T ′=T|U′，则子空间 (U′,T ′)为第二可数空间、第一可数空间、可分空间、Lindelof空间。

（2）设θi(i=1,2,…,n)为对称传递关系族，则乘积拓扑空间 (U×…×U，Tθ1×…×Tθn)为第二可数空间、第一可数空间、可分空间。

上述推论2～5来源于Tθ的四种可数特征（定理7）与经典拓扑性质（如2.2节）。推论2阐述可数性的拓扑不变性，推论3与4说明第一可数延展性质，推论5则聚焦子空间与乘积空间的结构制造（其中Lindelof空间不具有可乘性）。

5 实例分析

本章采用一实例来具体分析对称传递关系的诱导拓扑及其可数性。

例1设论域U={x1,x2,x3,x4,x5,x6}，二元关系

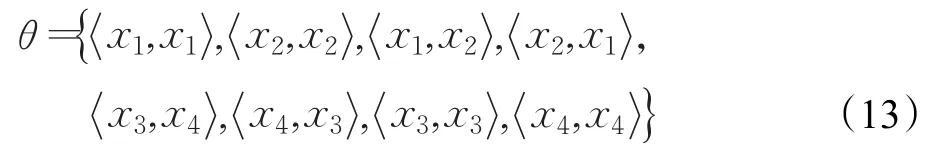
虽然θ满足对称性与传递性，但不满足自反性。因此，θ为U上的对称传递关系，而元素x5,x6为孤立点。

单点集的上近似集为：

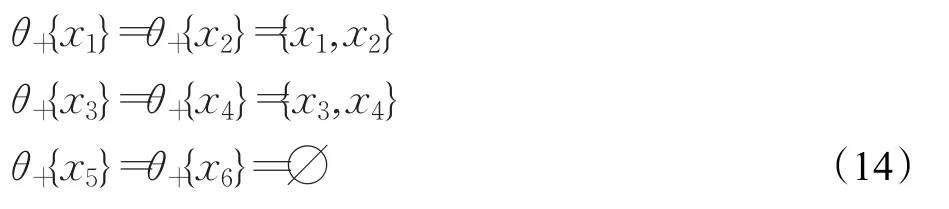
设 X={x2,x3,x4,x5}，Y={x1,x3,x4,x6}，Z={x1,x2}，则 X⋃Y={x1,x2,x3,x4,x5,x6}、X⋂Y={x3,x4}。

相关的上下近似集为：

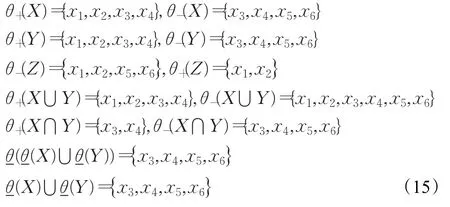
由此，可以验证命题2，例如：

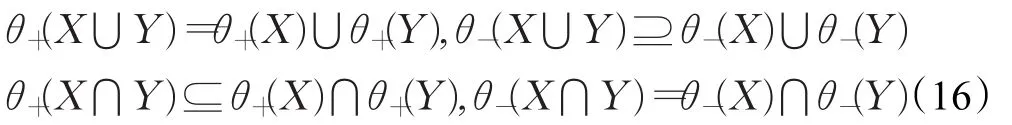
对称传递θ诱导拓扑为：

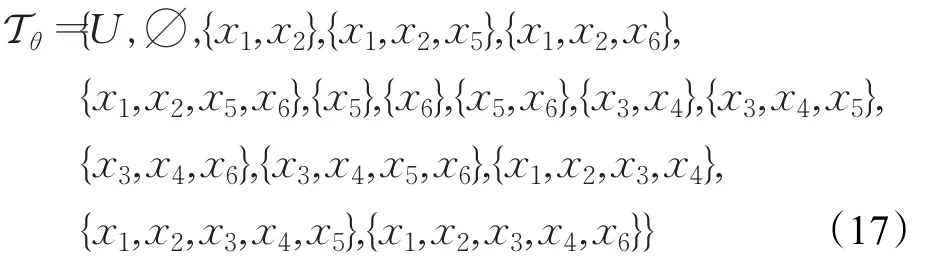
且θ+{xi}∈Tθ(i=1,2,3,4,5,6)。基于三种观测集计算，表1在上下近似集基础上提供Tθ内部与闭包结果，从而验证了两者之间的关系（定理4）。此外，表1标注部分开集与闭集来验证推论1。相关观测集的内部闭包与上下近似的复合：

]

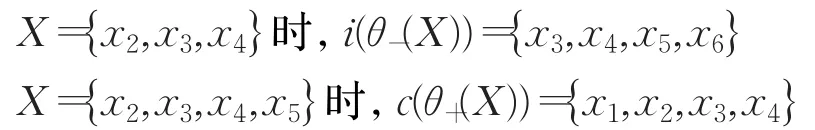
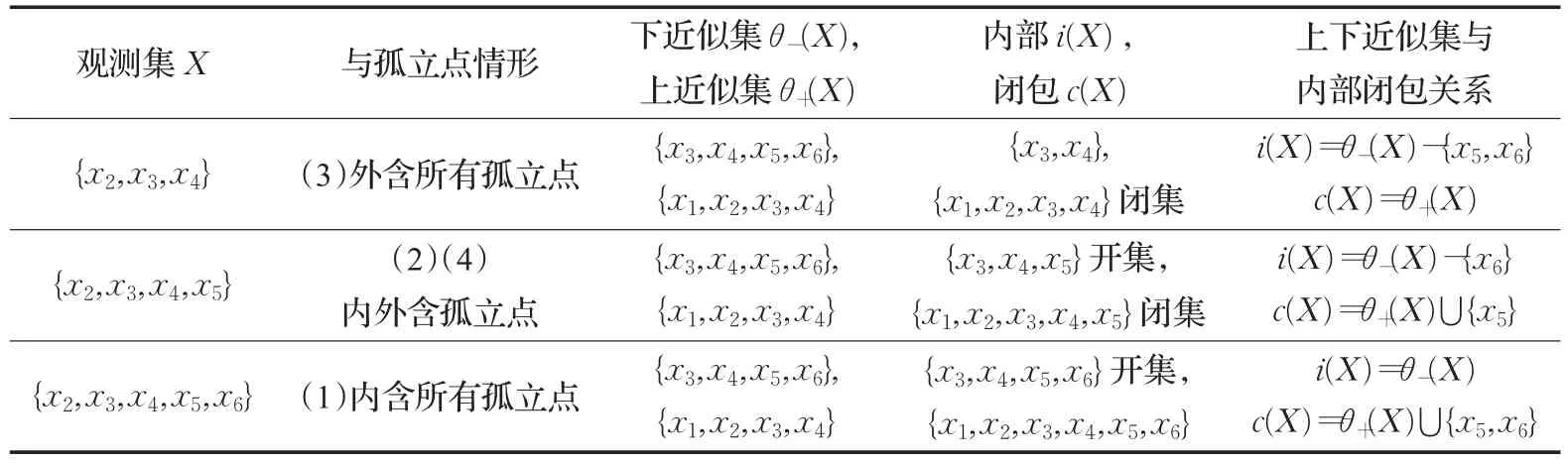
表1 三种观测集的上下近似集与拓扑内部闭包

在诱导拓扑空间(U,Tθ)中，可数基为：

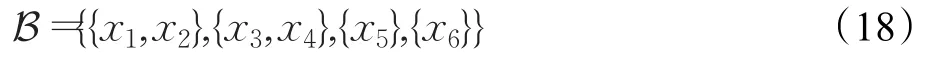
再考虑基

则有B⊆B′，该结果表明B最小性。x1∈U的邻域系为：

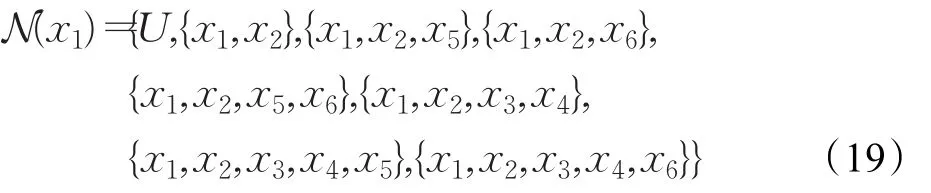
x1的可数邻域基为B(x1)={{x1,x2}}。考虑x1的邻域基：

则有B(x1)⊆B′(x1)，该结果表明B最小邻域基性。对本例诱导拓扑空间(U,Tθ)，可数基与可数邻域基的存在性确定了第二可数性与第一可数性，以及可分空间与Lindelof空间，即定理7被验证。基于经典拓扑结果，推论2～5自然成立，无需验证。

下面将比较分析本文结果与文献[11]结果。在文献[11]中，通过闭包算子与内部算子研究模糊粗糙集的拓扑结构，证明了自反、传递关系下的近似空间中模糊集的上下近似算子分别是一个模糊拓扑的闭包算子与内部算子，且相应的模糊拓扑满足（TC）条件。文献[11]主要讨论模糊集背景（其F(U)中的集合都是模糊集），而本文是在精确集下讨论基于对称传递关系的诱导拓扑及其可数性；对此，可以将文献[11]中的结论退化到精确集来与本文进行比较。特别地，表2提供了相关结果的异同点，其中Ρ(U)为U上的全体粗糙集的集合。

基于表2，两文结果的对比分析简单说明如下。（1）本文与文献[11]的相同点具有相同形式但不同背景。在相同点（1）中，两者的二元关系都是泛化的，但本文集合只涉及精确集，而文献[11]采用模糊集；在相同点（2）中，本文的二元关系仍是泛化的，但文献[11]的二元关系是定义的一种自反传递关系。（2）本文与文献[11]的不同点在形式与本质上都具有不同。在不同点（1）中，本文对于任意集合Y∈Ρ(U)，3集Y,θ-(Y),θ+(Y)无任何包含关系。同时，本文在对称传递关系下，削弱了i(θ-(X))和 i(X)、c(θ+(X))和 c(X)的包含关系。（3）将文献[11]的模糊集退化到精确集，可通过上述实例来进行相关比较，这里不再详述。

通过上面与文献[11]的比较分析，说明了在对称传递关系下的上下近似和拓扑的内部与闭包具有独特性质。

表2 本文结果与文献[11]结果的异同点

6 结束语

本文主要基于对称传递关系θ，确定近似集（算子）及其性质，构建诱导拓扑Tθ及其内部（算子）与闭包（算子）；进而，针对诱导拓扑Tθ提出基与邻域基研究可数性，得到第二可数性、第一可数性、可分性、Lindelof性等四种可数特征及其性质。本文采用一种新的二元关系拓展了粗糙集与拓扑的结合，深化了粗糙集与拓扑的联系。以基于对称传递关系，拓扑空间(U,Tθ)的其他拓扑性质可以深入。此外，一般拓扑需要什么条件以激发对称传递二元关系并反之对应诱导拓扑，值得思考。最后，根据图1，本文的工作完善了双性研究，而单性研究正是后续工作，并期待最终完成整个三性层次的系统分析。相应地，“基于对称传递的拓扑可数性特征”（如本文）与“基于自反、自反对称、自反传递等关系的特征”的区别，也成为后续工作。

参考文献：

[1]Pawlak Z.Rough sets[J].International Journal of Computer and Information Science，1982，11：341-356.

[2]唐小娟，丁树良.粗糙集理论在认知诊断中的应用[J].心理科学，2016（4）：790-795.

[3]王国虎，薛进学.基于粗糙集理论与支持向量机的多传感器信息融合方法[J].现代制造工程，2016（5）：59-62.

[4]王永生.基于粗糙集理论的动态数据挖掘关键技术研究[D].北京：北京科技大学，2016.

[5]葛浩.基于粗糙集的不协调决策系统知识约简研究[D].合肥：安徽大学，2016.

[6]叶回春，张世文，黄远仿.粗糙集理论在土壤肥力评价指标权重确定中的应用[J].中国农业科技，2014，47（4）：710-717.

[7]刘慧玲.基于粗糙集理论的齿轮箱故障诊断研究[D].太原：中北大学，2013.

[8]曹洪洋，任晓莹.基于粗糙集理论的区域降雨型滑坡预测预报[J].水文地质工程地质，2017（2）.

[9]桑秀丽，李哲，肖汉杰.肿瘤病理类型绿色诊断方法研究——基于变精度粗糙集与贝叶斯网络[J].统计与信息论坛，2015（4）：71-77.

[10]刘军凯，崔振新.基于粗糙集理论的飞机复飞事故影响因素分析[J].安全与环境工程，2017，24（2）：172-177.

[11]Zhang Yanlan，Li Changqing.Relationships between generalized rough sets based on covering and reflexive neighborhood system[J].Information Sciences，2015，319：56-67.

[12]马周明，李进金.严格局部自反关系下的广义粗糙集[J].计算机工程与应用，2011，47（29）：154-157.

[13]张宇.基于一般二元关系的几种粗糙集模型[D].辽宁锦州：渤海大学，2013.

[14]Pawlak Z.Rough sets：Theoretical aspects of reasoning about data[M].Boston：Kluwer Academic Publishers，1991.

[15]李招文，张珂.广义近似空间的拓扑结构[J].应用数学学报，2010，33（4）：750-757.

[16]乔全喜.粗糙集的拓扑结构研究[D].成都：西南交通大学，2013.

[17]于海，张瑞玲，詹婉荣.覆盖下近似算子的拓扑性质[J].模糊系统与数学，2012，26（3）：169-174.

[18]郑顶伟，蔡长勇.自反、传递（模糊）关系与拓扑空间[J].广西师范学院学报：自然科学版，2014，31（1）：28-30.

[19]Yao Yiyu.Two views of the theory of rough sets in finite universes[J].International Journal of Approximate Reasoning，1996，15（4）：291-317.

[20]Kondo M.On the structure of generalized rough sets[J].Information Sciences，2006，176：589-600.

[21]Qin Keyun.Generalized rough sets based on reflexive and transitive relations[J].Information Sciences，2008，178：4138-4141.

[22]Zhang Huapeng，Yao Ouyang，Wang Zhudeng.Note on“Generalized rough sets based on reflexive and transitive relations”[J].Information Sciences，2009，179（4）：471-473.

[23]秦克云，裴峥，杜卫峰.粗糙近似算子的拓扑性质[J].系统工程学报，2006，21（1）：81-85.

[24]吴志远.拓扑学在粗糙集理论中的应用[D].南昌：江西师范大学，2008.

[25]罗清君.逻辑代数系统的粗糙性与拓扑性质研究[D].西安：陕西师范大学，2014.

[26]熊金城.点集拓扑学[M].北京：高等教育出版社，2003.