改进的差分演化算法求解多维背包问题

吴聪聪，赵建立，2，刘雪静，陈嶷瑛

WU Congcong1,ZHAO Jianli1，2,LIU Xuejing1,CHEN Yiying1

1.河北地质大学 信息工程学院，石家庄 050031

2.全北国立大学 电子信息工程学院，韩国 全州 54896

1.College of Information Engineering,Hebei GEO University,Shijiazhuang 050031,China

2.School of Electronics&Information Engineering,ChonBuk National University,Jeonju 54896,Republic of Korea

1 引言

多维背包问题（The Multidimensional Knapsack Problem，MKP）是运筹学中一个典型的组合优化问题，广泛地应用于资源分配[1]、车辆装载[2]、经济[3]等领域。MKP问题是将n个物品放入背包中，每个物品i有一个非负价值 pi，并且占用m个维度的资源wi,1,wi,2,…,wi,m；背包也有m个维度，并且每个维度有一个资源的限制Cj，j={1,2,…,m}。要求选择若干物品装入背包，使得物品在每个维度不超过背包限制的前提下装入物品的价值和最大。用数学公式表示如公式（1）～（3）所示：

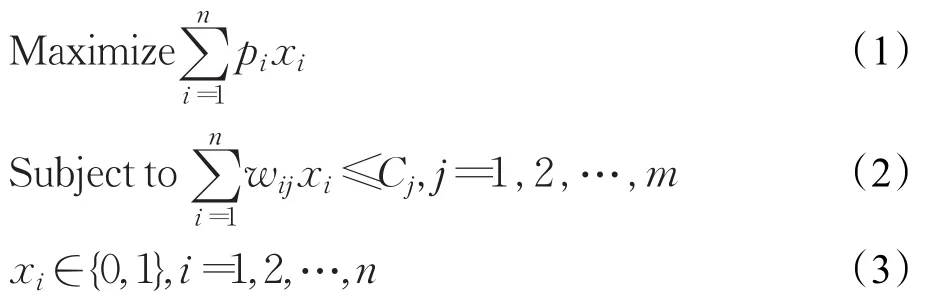
目前，解决MKP问题的方法主要分为两大类：一类是精确算法，一般用分支定界法[4-5]和动态规划法[6-7]；一类是用启发式算法[8-14]。由于精确算法在求解大规模数据时耗费的时间和空间开销都很大，所以不适合求解较大规模的MKP问题[9-10]，而启发式算法求解速度快，求解精度也能满足实际要求。最早使用启发式算法求解MKP问题的是文献[8]，他们使用GA算法求解MKP问题，证明了在适度的计算量的基础上可以得到较好的解。近年来涌现出很多求解MKP问题的启发式算法：基于PSO算法的求解法[11-12]、分布估计法[9]、改进的二进制果蝇算法[13]、人工鱼群[14]、二进制微分搜索法[10]等等。

求解精度和运算速度是求解MKP问题关注的核心，差分演化算法是一种优秀的全局优化的启发式算法，第一届国际演化计算（ICEO）竞赛中，差分演化算法被证明是速度最快的进化算法。但采用差分演化算法解决多维背包问题[15]的研究开展得却很少。本文提出了一种改进的二进制差分演化算法（Modified Binary Differential Evolution，MBDE）求解MKP问题，首先，设计了二进制差分演化算法（Binary Differential Evolution，BDE）的编码形式，使得差分演化算法能够解决离散问题；为提高算法的探索能力，加入了自适应反向测试搜索策略；另外，在此基础上，设计了一种精英局部搜索策略来提高求解精度和收敛速度；最后，为修复不可行解和优化可行解，采用一种更准确衡量物品有效价值的价值密度方法，并提出了贪心装载策略。为验证本文算法的有效性，进行了三组实验，和其他几种启发式算法进行比较，实验结果显示，本文提出的算法求解精度更高，从算法运行时间上看，MBDE算法求解速度非常快，适合求解大规模MKP问题。

2 二进制差分演化算法

差分演化算法[16-17]是众所周知的一种优秀的进化计算技术[18]，因其有效性使差分演化算法被广泛地应用于各个领域[19-23]。原差分演化算法主要用于解决连续函数的优化问题，要求解MKP问题，首先要解决算法的离散化问题，即编码问题。

2.1 编码设置和二进制差分算子的实现

在求解MKP的BDE算法中，种群中每个个体X=[x1,x2,…,xn]代表一个MKP的解，用一个n位二进制位串表示，每一位为0或1。受文献[13]和文献[24]的启发，在BDE算法中，每个个体X的每一个二进制位xi对应一个实数 p(xi)表示xi为1的可能性，每个个体X根据其对应的概率向量P(X)=[p(x1),p(x2),…,p(xn)]来确定，映射公式如公式（4）。

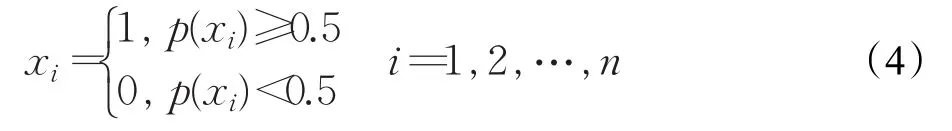
BDE算法和标准差分演化算法[16-17]一样主要包括变异、交叉、选择三个步骤，在BDE中，种群的变异操作由个体概率向量P(X)引导进行，变异公式如公式（5）。

其中P(Xk1),P(Xk2),P(Xk3)是三个和当前个体不同的另外三个个体对应的概率向量，F是取值范围在[0，1]之间的缩放比例因子。P(T)是变异产生的临时个体对应的概率向量，根据公式（4）将P(T)的值转换成中间临时个体T=[t1,t2,…,tn]。

在种群的交叉操作中，BDE算法对种群个体和其对应的概率向量同时处理，处理方法如程序片段1所示。差分算法中的交叉一般有两种形式：指数交叉和二项交叉。这里采用了类似于标准的DE算法[16]中的二项式交叉：首先对每一个变量都生成一个均匀分布在0到1之间的随机数rnd，如果rnd小于交叉因子Cr，则保留当前个体的原对应分量，否则接受临时个体的对应分量。

程序片段1

在选择算子中，BDE和标准的DE算法一样采用贪心选择方式，对于新临时个体T和当前个体X选择较好的个体进入下一代。

其中 fvalue是求个体适应度的函数，即公式（1）。

2.2 二进制差分演化算法流程

根据上面的说明，下面给出二进制差分演化算法的执行流程，如算法1。

算法1BDE算法

步骤1随机产生N个概率向量P(Xi)=[p(xi,1),p(xi,2),…,p(xi,n)]，i=1,2,…,N ，p(xi,j)∈[0,1)，根据公式（4）产生N个二进制个体Xi=[xi,1,xi,2,…,xi,n]，i=1,2,…,N，计算每个个体的适应度值。

步骤2对于种群中每个个体Xi和个体对应的概率向量P(Xi)：

（1）随机选择另外三个个体的概率向量根据公式（5）执行变异操作，再通过公式（4）生成临时个体Ti=[ti,1,ti,2,…,ti,n]。

（2）将临时个体Ti与当前个体按“程序段1”进行交叉操作。

（3）将交叉后的Ti与当前个体 Xi比较，选择较好的个体进入下一代。

步骤3如果终止条件满足，输出最优个体，否则返回步骤2。

从二进制差分演化算法的流程可以看出，和标准差分演化算法[16]一样，它具有记忆个体最优解和种群内信息共享的特点，通过保优贪婪策略保证了算法的收敛能力。在时间复杂度上，因为只是平行地增加了从实数向量（概率向量）向二进制向量的转换，所以和标准的差分演化算法的时间复杂度一样。如令算法的最大迭代次数为M，种群数为N，个体维度为n，则BDE算法时间复杂度为O(NMn)，是多项式时间的算法。

3 改进的二进制差分演化算法（MBDE）求解MKP问题

3.1 可行解的生成和优化

无论是初始化得到的随机个体，还是进化过程中得到的新个体，都会出现不满足约束条件的情况，通常称之为不可行解，对不可行解的修复是求解MKP问题的关键。目前有两种常用的方法对不可行解修复：一种是采用基于伪效用比率的修改机制[8]，其核心操作是代理对偶方法[25]。由于该修复方法需要先求得MKP对偶问题的最优解，加大了算法的计算量，降低了算法的效率[13]。另一种对不可行解修复的方法是依赖MKP问题本身的结构[8，13，26]确定物品伪使用率。这两种修复策略修复不可行解的过程都分为两步：第一步是按照某种次序将物品从背包中拿出，直到各维均不再超重，即得到了可行解；第二步是将没在背包中的物品依次试着装入背包，装入的过程中背包各维不能超重，如果超重就不装入。这两种方法一个共同的特点就是先要按照个体信息将物品装入背包，然后再调整（卸载+再装入），这种开始不考虑背包限制，而后再修正的方式，增加了计算的工作量。本文借鉴文献[27]中的GROA算法，基于MKP问题结构的特点，提出一种新的修复和优化方法——贪心装载法GLM（Greedy Load Method）。该方法在针对每个个体计算适应度值时使用，不用反复进行将物品装入和卸载的过程。下面详细介绍具体操作。

在MBDE算法中，对需要计算适应度值的每个个体进行GLM，即在计算个体的适应度值时，按照个体中的信息和物品的价值密度（也可以将价值密度看成伪使用率）将物品装入背包。价值密度是指单位重量的物品价值，对于多维背包，物品在多个维度相当于有多个重量，应该如何计算价值密度是值得分析的问题，选择一种能体现物品本身放入背包的性价比的价值密度会使GLM更有效。比较了几种价值密度设置方法后，本文采用物品价值与物品在背包各维度占重量比率和之比作为价值密度，如公式（7）所示。这不仅考虑了物品各个维度所占资源对价值密度的影响，同时加入了每个维度上物品与背包限制的关系影响，能更准确地体现物品的价值密度。

首先对物品按照价值密度从大到小排序，将排序后的物品序号写入vsort数组中。然后根据vsort中的序号顺序和差分算法中个体本身的信息将物品放入背包，前提是各个维度均不超出背包的限制。具体过程如算法2所示。vsort[i]表示价值密度排在第i位的物品的编号。X=[x1,x2,…,xn]是要计算适应度值的个体，B=[b1,b2,…,bn]是经过修复和优化后的个体，value是经过GLM计算的适应度值。

算法2GLM

整个修复过程可以看成两个阶段：第一个阶段是将个体选中的物品（该位为1）按价值密度由大到小的次序尝试装入背包；第二个阶段是将个体中没有选中的物品（该位为0）按价值密度由大到小的次序尝试装入背包，最后，得到修正和优化后的个体B。这种修复方法不但起到对不可行解修复的作用，同时对可行解有优化作用，并且不重复物品的装入过程，减小了计算量，从而提升了MBDE算法求解MKP问题的速度。从GLM算法的伪代码可以看出，第一阶段和第二阶段的时间复杂度都为O(nm)，所以GLM算法时间复杂度为O(nm)。其中n是物品数，m是背包的维度。一般用nm表示MKP问题的规模，所以GLM算法的时间复杂度和MKP的问题规模是线性关系。实验证明，此修复优化策略对大规模的MKP问题的求解产生了重要作用。

3.2 反向测试搜索

Tizhoosh[28]提出了反向学习（Opposition-based Learning，OBL）的概念，并认为智能搜索的最根本任务就是不断地学习、优化和搜索。反向学习的目的是扩大估计范围（同时评价当前解和反向解）从而得到更优秀的近似解。反向学习能够有效提高种群的多样性，对算法跳出局部极值有很大帮助。Rahnamayan等[29]将反向学习引入到差分演化算法中，主要用于种群初始化和子代产生中，提高了算法的收敛速度和求解精度。本文针对MKP问题，采用的反向学习策略与原OBL的方式有所不同，反向点的设置，主要针对个体的概率向量进行。二进制个体向量随之改变，具体定义如下：

定义1（反向点[28]）

设是d维搜索空间中的可行解，，那么它的反向点（反向解）

定义2（反向个体）

设Xi=[xi,1,xi,2,…,xi,n]是求解MKP问题的二进制个体，P(Xi)=[p(xi,1),p(xi,2),…,p(xi,n)]是其对应的概率向量，首先 ，求得个体Xi的反向概率向量，反向概率向量的各项可由公式（9）得到。之后，根据反向概率向量和公式（4）求得反向个体。然后利用 GLM 算法得到反向个体的适应度，如果该适应度大于原个体则由反向个体替换原个体，否则原个体不变。

公式（9）中，θ∈[0,1]是符合均匀分布的随机数。

3.3 精英局部搜索

群体中的精英个体和全局最优解之间的亲和度要大于群体中其他个体和全局最优解之间的亲和度，并且与精英个体有较大亲和度的个体也应有较高的适应度[30]。因此，精英个体对种群的进化起着重要的推动作用，充分利用精英个体的特征信息是保证算法性能的关键[31]。在精英个体周围展开精细搜索，可以加快算法寻优的速度和提高解的质量，增强MBDE的开发能力。

本文采用的精英局部搜索策略是：每次迭代后，随机选择全局最优个体的k位，使该位上的0，1互换，然后计算这个临时个体的适应度，如果其优于原最优个体，则由局部搜索得到的临时个体替代原最优个体。k值的选择表示着搜索区域离最优个体的远近，k值越大，表示距离越远。经过反复测试，本文选取k值为3，效果最好。因为是以精英个体为基础，这种看似简单的局部搜索，用很小的工作量却能达到很好的效果。

3.4 求解MKP问题的MBDE算法流程

通过以上几节的阐述，可以综合得到求解MKP问题的改进的差分演化算法。下面用“(Xi,f(Xi))←GLM(Xi)”表示对个体Xi使用GLS算法修复和优化并得到目标函数值（也是适应度）f(Xi)；用“vsort[1…n]←QuickSort({d(v1),d(v2),…,d(vn)})”表示n个物品按照价值密度d(vi)，i=1,2,…,n，由大到小排序后将物品下标依次存入数组vsort[1…n]中；则MBDE算法求解MKP问题的流程描述如算法3所示。

算法3MBDE求解MKP

步骤1初始化

（1）随机产生 N个概率向量 P(Xi)=[p(xi,1),p(xi,2),…,p(xi,n)]，i=1,2,…,N ，p(xi,j)∈[0,1)，根据公式（4）生成N个二进制个体Xi=[xi,1,xi,2,…,xi,n]，i=1,2,…,N ，(Xi,f(Xi))←GLM(Xi),i=1,2,…,N 。

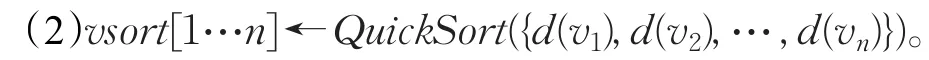
步骤2变异和交叉

对于种群中每个个体Xi和个体对应的概率向量P(Xi),i=1,2,…,N：

（1）随机选择另外三个个体，将三个个体对应的概率向量根据公式（5）执行变异操作，再通过公式（4）生成临时个体Ti={ti,1,ti,2,…,ti,n}。

（2）将临时个体Ti与当前个体按“程序段1”进行交叉操作。

步骤3反向测试搜索

对于种群中每个个体Xi和个体对应的概率向量P(Xi),i=1,2,…,N ：

（1）按公式（9）和公式（4）求得反向个体对应的概率向量和反向个体。

步骤4精英局部搜索

（1）Xbest=种群最优个体。

（2）随机选择的Xbest的3位进行0，1互换得临时个体 Xtemp，(Xtemp,f(Xtemp))←GLM(Xtemp)。

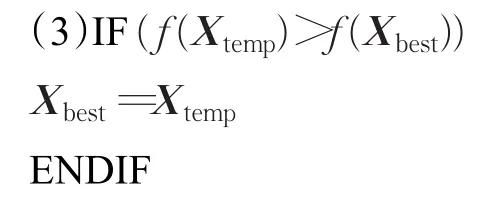
步骤5如果达到最大迭代次数，则RETURN(Xbest)，否则返回步骤2。

在MBDE算法中，步骤1是初始化工作，生成初始群体并使用贪心装载法GLM计算个体适应度，使用快速排序方法对物品按价值密度排序，总的时间复杂度为O(Nn+Nnm+nlbn)；步骤2是二进制差分演化算法的交叉、变异和选择操作，时间复杂度为O(Nn+Nnm)；步骤3是对个体进行反向搜索，时间复杂度为O(Nn+Nnm)；步骤4是在精英个体周围进行局部搜索，时间复杂度为O(nm)；故MBDE算法的时间复杂度为O(Nn+Nnm+nlbn)+M×(2O(Nn+Nnm)+O(nm))。这里N为种群规模，M为最大迭代次数。

4 仿真实验

为测试算法MBDE的性能，本文使用世界上广泛使用的 Benchmark数据集（http：//www.cs.nott.ac.uk/～psxjd2/mkp/index.html），第1个数据集包括5个混合规模测试实例，第2个数据集包括30个中等规模测试实例，背包数量为5，物品数为30～90；第3个数据集包括11个大规模实例，物品数量从100到2 500。所有这些实验采用C++编码，每个实例独立运行50次，计算平台为：Intel Core™i7（主频 2.6 GHz），4 GB RAM，Microsoft Windows 10。

4.1 参数的选择

任何启发式算法都有两个重要的参数：种群规模和最大迭代次数，虽然较大的种群规模和迭代次数可以获得更好的解，但会增加时间消耗，所以选择种群规模为30，最大迭代次数为2 000次。在MBDE算法中另外两个参数是缩放因子F和交叉因子Cr，为每个参数设置了5个可能的值。使用一个中等规模的实例sento2（背包数目30个，物品数60个）用口田实验法[32]对参数进行测试选择。表1给出了测试的正交矩阵L25（52），avg是每个参数组合独立运行程序100次求得的平均值。

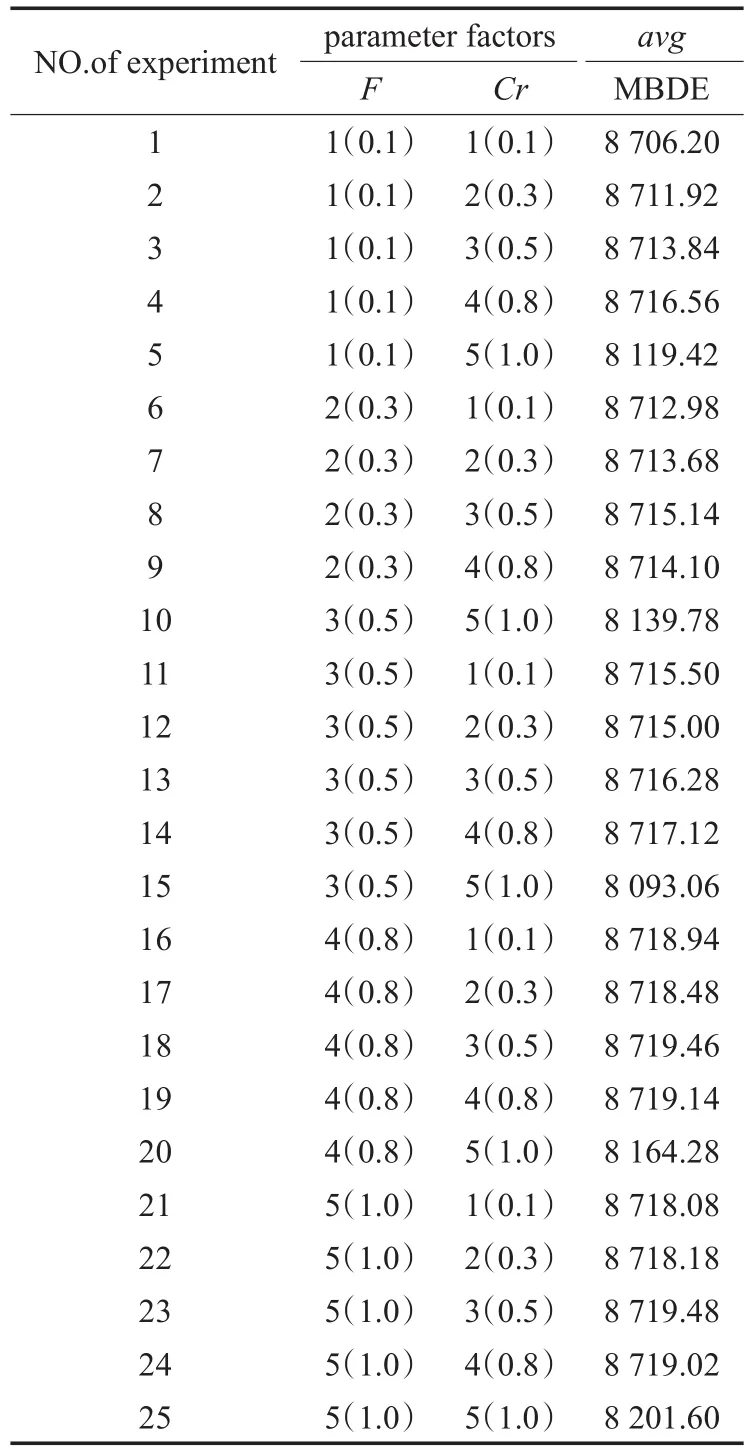
表1 正交矩阵和MBDE的平均运行结果

根据正交表（表1）得到参数选择实验的极差分析表（表2）和参数水平对实验结果的影响趋势图（图1，图2），从表2和图1中可以看出，参数Cr的影响比F大，主要体现在当Cr取第5种值时（即Cr=1.0）算法取得的平均值非常低。也就是说在算法的交叉过程中，没有一位来自新产生的临时个体而全部来自原个体的情况下，算法效果最差。Cr取其他值而得到的结果基本相当，但很明显在取第4种(Cr=0.8)时算法达到最好。所以在后面的实验中参数设置为：F=1.0，Cr=0.8。

表2MBDE参数选择极差分析表

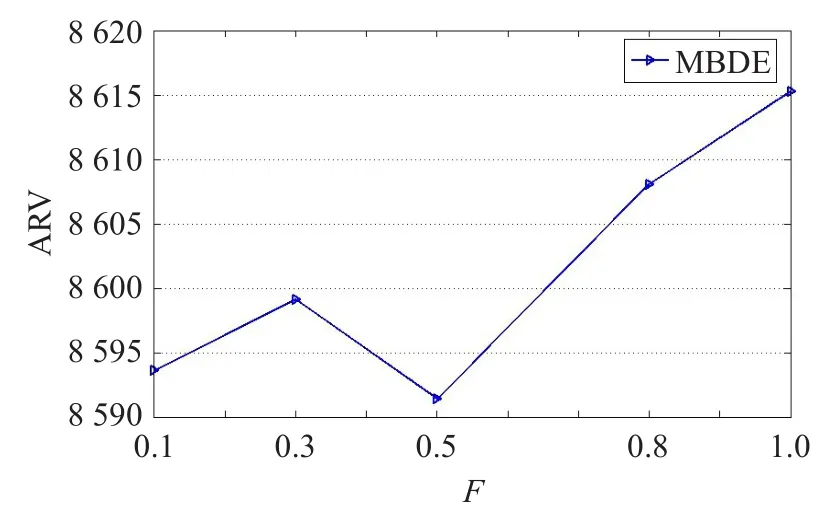
图1 MBDE参数F各取值对结果的影响趋势

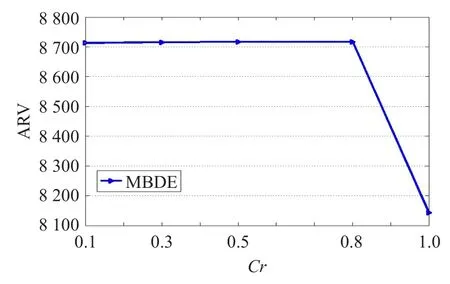
图2 MBDE参数Cr各取值对结果的影响趋势

4.2 实验结果统计与比较

表3～表5展示了算法对3组实例进行测试的结果，为比较算法MBDE的性能，在表3～表5中与近期发表的其他启发式算法的求解结果进行比较，在各表中problem列是实例的名称；n×m列是实例的规模，其中n是物品数，m是背包的维度；Opt列是实例的目前已知最优值；SR列是成功率；Mean列是平均值，Std列是标准差，ACT列是平均执行时间。各表中其他启发式算法的实验数据分别来自文献[9-10，13，15]。

表3 MBDE算法与SD-BDE算法求解MKP问题比较

表4 MBDE求解数据集2实验结果及比较

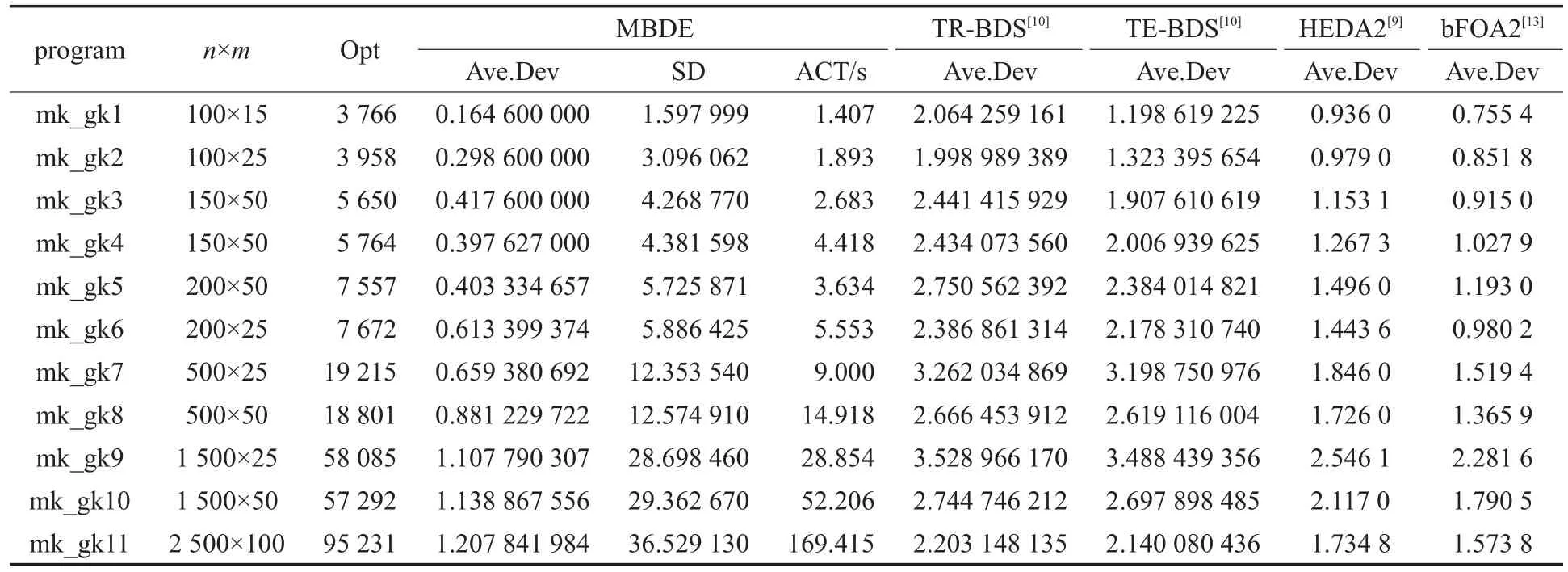
表5 MBDE求解数据集3实验结果及比较

首先，基于测试集1测试算法MBDE的性能，并与文献[15]中的随机扩散二进制差分算法（SD-BDE）进行比较，对每个实例，独立运行50次，统计成功率和平均值，SD-BDE的实验数据来自文献[15]。

从表3中可以明显看出，MBDE对各个实例的求解成功率和平均值均远远高于SD-BDE算法，其中有三个实例成功率达到1，其他两个实例的成功率也都在0.80以上，说明MBDE有很好的鲁棒性。

表4是算法对中等规模测试数据集2的30实例的测试结果和与文献[10]中随机二进制微分算法（TRBDS）和精英二进制微分算法（TE-BDS）进行比较的情况。MBDE算法有26实例求解成功率为1，TR-BDS算法有10个实例成功率为1，TE-BDS只有3个实例成功率达到1。说明MBDE对中等规模的数据求解能力非常强。从求解的方差看，MBDE除实例6的方差略高于TR-BDS算法外，其他实例求解的方差均低于TE-BDS和TR-BDS，说明算法MBDE有很好的稳定性。从ACT上分析，除了在实例weish06和weish26上的平均执行时间为1秒多，算法在每个实例上的平均执行时间都不超过1秒，说明MBDE的求解效率非常高。

为进一步考察MBDE的性能，表5是MBDE求解大规模MKP问题测试集3的实验结果，通过平均偏差（Ave.Dev）来对算法MBDE与文献[10]的TR-BDS与TE-BDS，文献[9]的HEDA2和文献[13]的FOA2进行比较。平均值偏差是指每个实例独立运行若干次，求得最优值的平均值与已知最优值的偏差的百分比（平均偏差=（已知最优值-平均值）/100），所以平均偏差越小说明算法的求解性能越好。从几个算法的平均偏差看，MBDE算法在11个大规模实例中均都低于其他4种算法，MBDE性能最好。为了进一步分析算法MBDE的稳定性和效率，这里求出50次独立运行MBDE得到的最优值的方差，50次独立运行中算法每次执行的平均时间。从方差看，虽然随着问题规模的增大有所增加，但增加的幅度不大，总体看方差很小，说明算法的稳定性非常好。从平均执行时间ACT看，除了mk_gk11花费的时间较长，但也没有超过4 min，其他实例求解时间都不超过1 min。这说明算法能有效求解较大规模的MKP问题。

以上的实验数据比较可以说明，算法MBDE对于求解各种规模的MKP问题具有很强的鲁棒性和寻优能力。

5 结束语

本文提出了一种求解MKP问题的改进的二进制差分算法，提出了一种新的价值密度计算方法，并设计了一种修复不可行解和优化可行解的方法，算法中加入反向搜索提高算法的开发性能，精英局部搜索提高算法探索能力，有效提高了算法对MKP问题的求解精度和收敛速度。基于国际标准测试数据的仿真实验表明，MBDE无论对于中小规模MKP问题，还是大规模MKP问题，均具有优良的寻优能力和较强鲁棒性以及求解速度。和近期提出的解决MKP问题的其他较优秀的启发式算法（随机二进制差分算法、随机二进制微分算法、精英二进制微分算法，混合分布估计法、混合果蝇算法）进行了比较，比较结果显示MBDE算法求解精度和效能更高，是一种更有效地求解MKP问题的算法。

参考文献：

[1]Wu Changzhi，Wang Xiangyu，Lin Jiang.Optimizations in project scheduling：A state-of-art survey[M]//Optimization and Control Methods in Industrial Engineering and Construction.Dordrecht：Springer，2014：161-177.

[2]Nawrocki J R，Complak W，Ewicz J B A，et al.The knapsack-lightening problem and its application to scheduling HRT tasks[J].Bulletin of the Polish Academy of Sciences Technical Sciences，2010，57（1）：71-77.

[3]Martello S，Touth P.Knapsack problems：Algorithms and computer implementations[M].New York：Wiley，1990.

[4]Shih W.A branch and bound method for the multiconstraint zero-one knapsack problem[J].Journal of the Operational Research Society，1979，30（4）：369-378.

[5]Freville A，Plateau G.The 0-1 bidimensional knapsack problem：Towards an efficient high-level primitive tool[J].Journal of Heuristics，1996，2：147-167.

[6]Touth P.Dynamic programing algorithms for the zero-one knapsack problem[J].Computing，1980，25（1）：29-45.

[7]Balev S，Yanev N，Freville A，et al.A dynamic programming based reduction procedure for the multidimensional 0-1 knapsack problem[J].European Journal of Operational Research，2008，166：63-76.

[8]Chu P C，Beasley J E.A genetic algorithm for the multidimensional knapsack problem[J].Journal of Heuristics，1998，4（1）：63-86.

[9]Wang Ling，Wang Shengyao，Xu Ye.An effective hybrid EDA-based algorithm for solving multidimensional knapsack problem[J].Expert Systems with Applications，2012，39（5）：5593-5599.

[10]Liu Jianjun，Wu Changzhi，Cao Jiang，et al.A binary differential search algorithm for the 0-1 multidimensional knapsack problem[J].Applied Mathematical Modelling，2016，40（23/24）：9788-9805.

[11]Bansal J C，Deep K.A modified binary particle swarm optimization for knapsack problems[J].Applied Mathematics Computation，2012，218（22）：11042-11061.

[12]Chih M.Self-adaptive check and repair operator-based particle swarm optimization for the multidimensional knapsack problem[J].Applied Soft Computing，2015，26：378-389.

[13]Wang Ling，Zheng Xiaolong，Wang Shengyao.A novel binary fruit fly optimization algorithm for solving the multidimensional knapsack problem[J].Knowledge-Based Systems，2013，48（2）：17-23.

[14]Azad M A K，Rocha A，Fernandes E.Improved binary artificial fish swarm algorithm for the 0-1 multidimensional knapsack problem[J].Swarm&Evolutionary Computation，2014，14：66-75.

[15]Salman A A，Ahmad I，Omran M.Stochastic diffusion binary differential evolution to solve multidimensional knapsack problem[J].International Journal of Machine Learning and Computing，2016（2）：130-133.

[16]Storm R，Price K.Differential evolution—a simple and efficient adaptive scheme for global optimization over continuous spaces[R].International Computer Science Institute，1995.

[17]Storn R M，Price K V.Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces[J].Journal of Global Optimization，1997，11（4）：341-359.

[18]王凌，钱斌.混合差分进化与调度算法[M].北京：清华大学出版社，2012.

[19]Joshi R，Sanderson A C.Minimal representation multisensor fusion using differential evolution[J].IEEE Trans on Systems，Man and Cybernetics，Part A，1999，29（1）：63-76.

[20]Abbass H A.An evolutionary artificial neural networks approach for breast cancer diagnosis[J].Artificial Intelligence in Medicine，2002，25（3）：265-281.

[21]Kapadi M D，Gudi R D.Optimal control of fed-batch fermentation involving multiple feeds using differential evolution[J].Process Biochemistry，2004，39（11）：1709-1721.

[22]Aydin S，Temeltas H.Fuzzy-differential evolution algorithm for planning time-optimal trajectories of a unicycle mobile robot on predefined path[J].Advanced Robotics，2004，18（7）：725-748.

[23]Tsaiky，Wang F S.Evolutionary optimization with data collocation for reverse engineering of biological networks[J].Bioinformatics，2005，21（7）：1180-1188.

[24]贺毅朝，王熙照，寇英展.一种具有混合编码的二进制差分演化算法[J].计算机研究与发展，2007，44（9）：1476-1484.

[25]Pirkul H.A heuristic solution procedure for the multiconstraint zero-one knapsack problem[J].Naval Research Logistics，1987，34（2）：161-172.

[26]Zhang Biao，Pan Quanke，Zhang Xinli，et al.An effective hybrid harmony search-based algorithm for solving multidimensional knapsack problems[J].Applied Soft Computing Jounal，2015，29（C）：288-297.

[27]贺毅朝，王熙照，李文斌，等.基于遗传算法求解折扣背包问题的研究[J].计算机学报，2016，39（12）：2614-2629.

[28]Tizhoosh H R.Opposition-based learning：A new scheme for machine intelligence[C]//Proceedings of IEEE Computational Intelligence for Modelling，Control and Automation，Vienna，Austria，2005：695-701.

[29]Rahnamayan S，Tizhoosh H R，Salama M M A.Opposition-based differential evolution[J].IEEE Transactions on Evolutinary Computation，2008，12（1）：64-79.

[30]孟伟，韩学东，洪炳.蜜蜂进化型遗传算法[J].电子学报，2006，34（7）：1294-1300.

[31]刘全，王晓燕，傅启明，等.双精英协同进化遗传算法[J].软件学报，2012，23（4）：765-775.

[32]Wadley F M.The design and analysis of experiments[J].Yale Journal of Biology&Medicine，1953，6（5）：18.