基于超效率SBM-Malmquist方法的城市轨道交通效率分析比较研究

郑又源，刘延平，何砚



基于超效率SBM-Malmquist方法的城市轨道交通效率分析比较研究

郑又源1，刘延平2，何砚3

（1.西安电子科技大学 经济与管理学院，陕西 西安 710071；2.中国传媒大学，北京 100024；3.北京市社会科学院 经济所，北京 100101）

本文应用超效率SBM模型对我国17个中心城市的轨道交通效率进行了评价，得出了各城市轨道交通建设运营的相对效率值、排名和松弛改进值；为检验评价结果的稳健性，本文利用投入导向的超效率BCC模型与超效率SBM模型的结果进行了比较，比较结果显示，超效率SBM模型得出的排名是稳健可靠的。在超效率SBM模型的效率值基础上，本文应用序列参比法计算出了Malmquist指数，并将其与相邻参比法计算的Malmquist指数进行了比较，比较结果显示相邻参比Malmquist指数更适用于测评城市轨道交通业。

超效率SBM模型；Malmquist指数；城市轨道交通效率；序列参比法；相邻参比法

一、引言

随着我国城市化进程的不断加快，城市交通资源供求矛盾也日益凸显，交通拥堵问题已成为影响城市可持续发展的巨大障碍。轨道交通以其运量大、污染低、高效便捷的优点成为各大城市解决交通问题优先考虑的方案。然而，轨道交通投资大、周期长，轨道交通的运行效率是项目决策中必须慎重考虑的问题，那么如何客观评价轨道交通的效率就是这个问题的核心。

对一个行业的效率进行评价分析，数据包络分析（DEA）是应用最为广泛的一种非参数方法。DEA依据线性规划原理，对具有相同投入产出的决策单元（DMU）的相对效率进行估计测算，不仅具有稳健性，而且适用于小样本分析[1]，因此，近年来国内外许多学者将DEA方法应用于城市交通的效率评价。国外学者如Barnum和McNeil运用DEA方法对芝加哥交通体系的停车换乘效率进行了评价[2]；Michaelides等应用随机前沿分析法和DEA法两种方法分析了希腊雅典和比雷埃夫斯的无轨电车运营效率，并对两种分析方法进行了比较[3]；Vaidya应用层次分析法和DEA法分析了印度26个城市公共交通组织的效率[4]；Wanke应用二阶段随机DEA法和Beta回归法对全世界285个城市的交通模式进行了效率评价[5]。国内学者如王亚华等应用Malmquist-DEA方法测算了中国交通全行业及主要部门1980-2005年的生产率，并引入Bootstrap-DEA方法估计了技术效率的变化[6]；王欢明和诸大健采用DEA-Tobit方法对长三角城市间公交服务的运营效率进行的评价[7]；王海燕等将Gini准则引入DEA，并以此DEA-Gini方法对南京市公交企业的绩效进行了评价[8]；李学文等则采用超效率DEA-Gini方法对我国31个城市的公共交通业2006-2012年的效率进行了评价[9]；章玉等采用三阶段DEA对中国35个中心城市2010-2013的城市公共交通效率进行了评价[10]。随着轨道交通的发展，越来越多的城市开始拥有道路公交和轨道交通两套并行的公交系统，轨道交通系统是一个相对独立的运输系统，部分学者开始将DEA方法专门用于对轨道交通的效率进行评价。国外学者如Swami用DEA方法评价了德里市地铁站的效率[11]；国内学者如周强等用DEA方法对全国16个城市的轨道交通系统进行了效率评价[12]；李磊和姚璇宇用DEA法对我国10个城市2010-2011年的轨道交通运行效率进行了评价，并采用Malmquist指数分析了2005-2011年间轨道交通全要素生产率的差异及变动趋势[13]。

已有文献对于轨道交通行业效率评价的研究无疑有着重要的借鉴意义，但是有以下三点不足：第一，已有文献大多以CCR或BCC这一类经典DEA模型为分析工具，而这一类DEA模型在估计最优生产前沿面时，构成前沿面的决策单元效率值均为1，这样就无法进一步的比较效率值为1的各单元间效率的差异。第二，传统CCR或BCC模型为径向模型，对无效率程度的测量只包括了等比例改进的部分，未包括松弛改进的部分。第三，已有的文献以静态分析为主，动态分析较少。

为了克服第一点不足，本文采用超效率DEA模型进行效率评价，避免效率值过多处于极端值1的情形，提高了模型对城市公共交通效率的区分度。为了克服第二点不足，本文采用SBM-DEA模型进行效率评价，并与传统的径向模型评价结果进行比较。为了克服第三点不足，本文采用面板数据，引入Malmquist全要素生产率指数，动态的测算分析被评价城市公共交通业全要素生产率的变化并分解其中的效率变化因素与技术进步因素。

二、研究方法

（一）超效率SBM模型

DEA是一种评价决策单元“相对效率”的非参数线性规划分析方法，该方法最早由Charnes等学者提出，被称为CCR模型[14]，随后Banker等学者在此基础上发展出了基于规模收益可变（VRS）的BCC模型，CCR和BCC模型是应用最为广泛的两类基本模型[15]。然而DEA基本模型在测评效率值时，无法比较区分同处于最优前沿生产面上的决策单元的相对效率，为了解决这一问题，Andersen和Petersen提出了超效率DEA模型[16]。超效率模型的思想是将被评价的DMU从参考集中剔除，通过参考其它DMU的构成前沿对该DMU进行评价，计算出的效率值大于1，可以对已经判为有效的DMU进行再区分，从而克服传统DEA模型的不足。本文拟对不同城市公共交通行业的效率进行排名，超效率DEA模型恰好可以对处在交通投入——产出最优前沿面的城市效率进行进一步的区分。但是基于CCR或BCC的径向超效率模型仍有缺点，即未考虑到松弛变量的问题，为改进这一缺点，学者Tone提出了超效率SBM模型[17]。考虑到轨道交通有可能出现的规模产出变化，本文采用基于规模收益可变的超效率SBM模型进行分析：

假设存在个决策单元（DMU），每个DMU有种要素投入和类产出，对于第个DMU，其超效率投入——产出效率值可以通过如下的规划模型求解：

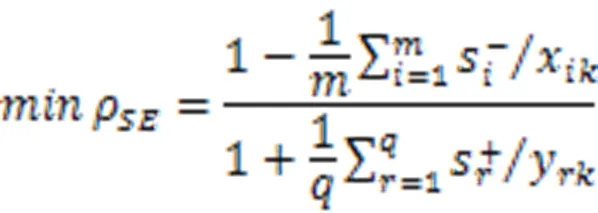
（二）Malmquist全要素生产率指数分析

当被评价的DMU数据为包含多个时间点观测值的面板数据时，可以进一步对生产率的变动情况以及技术效率与技术进步两方面因素对生产率变化所起的作用进行分析，这就是Malmquist全要素生产率指数分析。Malmquist指数的概念由Malmquist提出[18]，Caves等学者将Malmquist指数应用于生产率的测算[19]，Färe等学者则首次采用DEA方法计算Malmquist指数，并将其分解为技术效率的变化（EC）和生产技术的变化（TC）[20]。Färe等的Malmquist指数是采用相邻参比法再经过几何平均求得的，当评价样本比较小时，样本的有效前沿不一定前移，这就可能会出现指数分解后的技术变化呈现“技术后退”这种与经济理论不符的情形。为了避免此问题，我们拟采用Shestalova的序列参比法计算Malmquist指数[21]。

序列参比法与相邻参比以及其他方法相比，其主要改进之处在于对DMU的参考集进行了扩充，每期的参考集不仅包含本期的参考集，还包含之前所有时期的参考集，即：

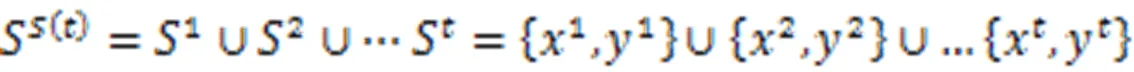
这样，构成+1期的有效前沿的DMU中包含了期的DMU，因此+1期的有效前沿与期相比肯定不后退。这里为投入向量，为产出向量。从时期到+1时期的序列前沿交叉参比Malmquist指数可定义为：

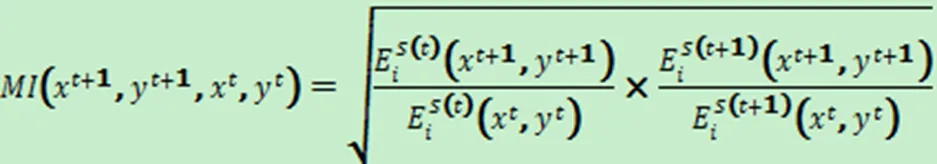
这里E（）（xy）为决策单元在时期，以S（）1∪2∪…S+1为参考集的DEA效率值；同理， E（）（x1y1）为决策单元在+1时期，以S（）为参考集的DEA效率值。E（+1）（xy）为决策单元在时期，以S（+1）1∪2∪…S+1为参考集的DEA效率值；同理，E（+1）（x1y1）为决策单元在+1时期，以S（+1）为参考集的DEA效率值。Malmquist指数可以进一步分解为效率变化（EC）和技术变化（TC）两部分，其中：

三、评价样本与评价指标

轨道交通在我国中并未完全普及，但是却发展迅速，自2010年起，每年都有城市建成首条轨道线路，实现轨道交通的从无到有，这会导致被评价DMU样本跨期不一致，使得样本评价不可比。因此，我们综合考虑数据的可获得性以及DEA模型以及Malmquist指数分析对DMU样本的要求，选择自2013年始即拥有轨道交通的全国17个中心城市，即15个省会城市（北京、天津、沈阳、长春、哈尔滨、上海、南京、杭州、郑州、武汉、广州、重庆、成都、昆明、西安）和大连、深圳两个计划单列市2013-2015年的轨道交通数据为研究样本，数据来源为《中国交通运输统计年鉴》（2013-2015）。

评价指标的设定我们遵循以下思路：从轨道交通的人员、载具、基础设施三个方面选择投入指标，从轨道交通的总里程与总运量两个方面选择产出指标。具体指标的设置又参考了周强与李磊和姚璇宇等学者的指标体系[12-13]，具体投入产出指标及其描述性统计量如表1所示：

表1：轨道交通投入产出指标及其描述性统计量（2013-2015）

四、城市轨道交通超效率DEA评价结果与比较分析

（一）超效率SBM模型评价结果与分析

我们使用MaxDEA 7 Ultra软件求解超效率SBM模型，得到2013-2015年我国17个中心城市轨道交通的相对效率及排名，如表2所示：

从表2报告的效率评价结果来看，在17个中心城市中，2013-2015年分别有9个、9个、10个城市的轨道交通投入产出相对效率值大于1，即达到了DEA有效，超过半数的中心城市实现了轨道交通建设运营的相对有效。北京、长春、哈尔滨、郑州、广州5个城市的轨道交通在2013-2015年全部实现DEA有效，其中哈尔滨的轨道交通相对效率在这三年中稳居第一，北京、广州的相对效率排名也稳居前三甲，长春、郑州的排名则稳定在第四至第七之间。沈阳、南京、成都3个城市轨道交通则在这三年内全部未达到DEA有效，相对效率排名全部在10名以后。另外两个城市武汉与深圳的轨道交通相对效率在2013-2015年排名也相对稳定，武汉市的效率排名稳中有升，深圳市的排名则稳定在第九、第十名。

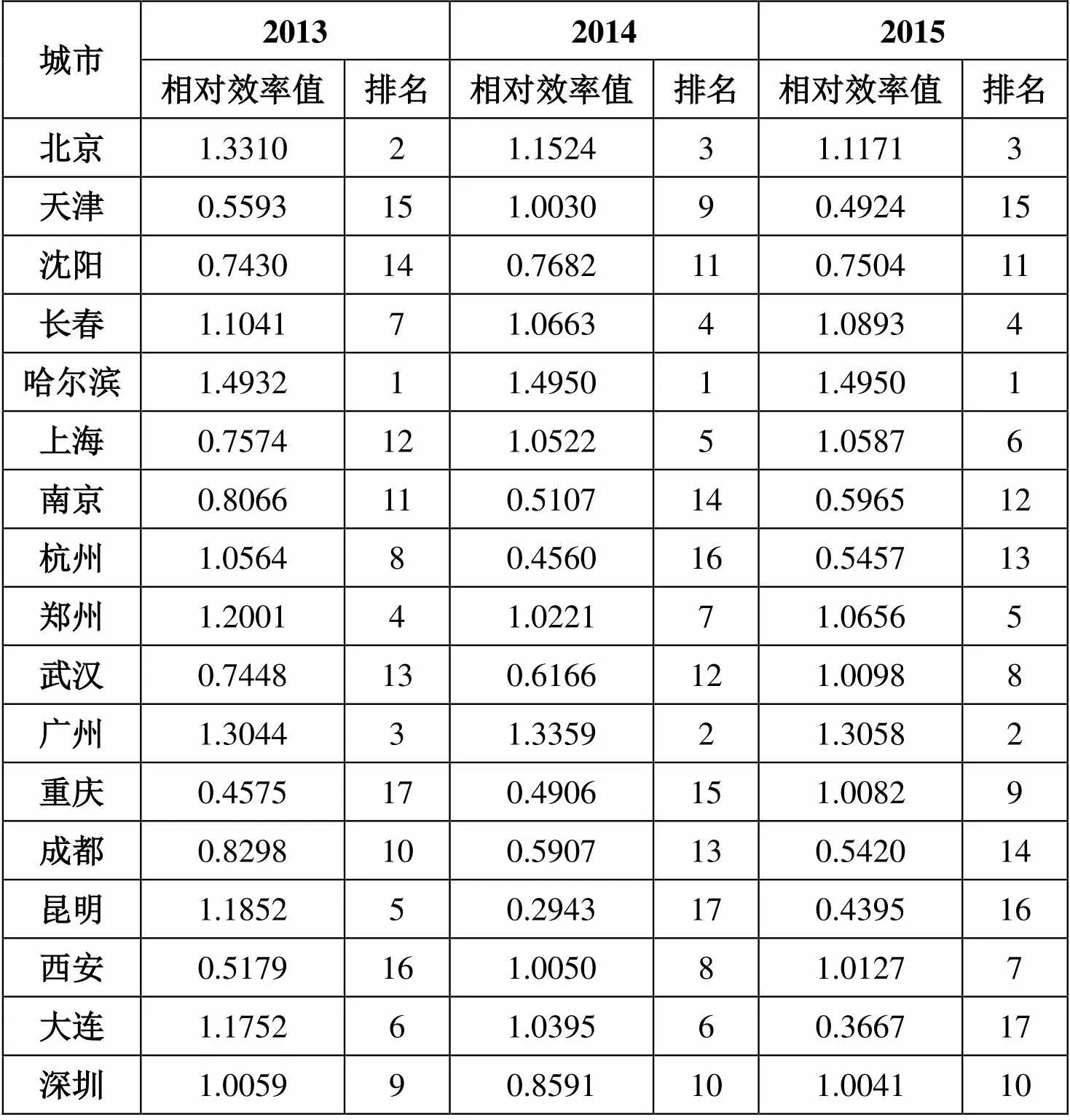
表2：城市轨道交通超效率SBM模型评价效率值与排名

天津、上海、杭州、重庆、昆明、西安、大连7个城市的轨道交通相对效率排名在2013-2015年波动较大，并且情况各有不同。天津市轨道交通2013年处于相对无效状态，排名处于15位，2014年相对效率上升，达到相对有效，排名也提升至第九位，但是2015年又回归至2013年的状态与排名。上海市和西安市情形相似，两市2013年轨道交通处于相对无效的状态，排名也较靠后，但是2014年相对效率及排名均显著上升，效率状态都达到了相对有效，2015年效率状态及排名基本保持在2014年水平。杭州市与昆明市情形相似，两市2013年轨道交通处于相对有效的状态，排名也较靠前，但是2014年相对效率出现断崖式下降，效率状态均为相对无效，排名也下滑至最末两位，2015年两市轨道交通的相对效率值有所回升，但是效率状态及排名与2014年相比无显著变化。重庆市和大连市的情形完全相反，重庆市2013、2014年轨道交通处于相对无效的状态，排名也较靠后，但是2015年相对效率及排名均显著上升，效率状态达到了相对有效，大连市的情况则与重庆市完全相反。

根据SBM模型，我们还可以得出各城市轨道交通各项投入产出的有效目标值和松弛改进值，如表3所示：

表3：中心城市2013-2015年各投入产出指标松弛改进值

（二）超效率SBM模型与超效率径向模型结果比较

为了检验超效率SBM模型的适用性及其评价结果的稳健性，我们又使用以投入为导向的超效率VRS（BCC）模型对17个中心城市的轨道交通效率进行了评价，并将其评分及排名结果与超效率SBM模型的评价结果进行了对比，具体结果如表4所示：

表4：超效率SBM模型与超效率BCC模型评价结果比较

从表4报告的结果可以看出：

第一，超效率BCC模型在测算北京市的轨道交通效率时出现了无可行解的情况，这反映超效率SBM模型对于本案数据的分析评价能力要强于超效率BCC模型，前者更适用于评价轨道交通的效率。对于超效率径向VRS模型无可行解的原因，Seiford和Zhu[22]作了深入探讨，本文不再赘述。

第二，超效率SBM模型计算出的相对效率值要小于超效率BCC模型，这是由于SBM模型中被评价DMU的投影点是有效前沿距离该DMU距离最远的点，换言之SBM模型使得被评价DMU的“无效率程度”达到最大，那么反之测算出的效率值就是最小的。从某种意义上讲SBM模型估计了被评价DMU的相对效率的下限。

第三，除去北京市无法评价排名之外，两种DEA模型对其余16个城市的效率排名总体差异很小，只有2014年昆明市的排名与2015年昆明、大连两市的排名差异较大。两种模型排名结果较高的一致性可以说明我们对于全国17个中心城市2013-2015年轨道交通的建设运营效率的排名是稳健可靠的。

五、城市轨道交通的Malmquist全要素生产率指数测算与比较分析

（一）序列参比Malmquist指数测算、分解和分析

在SE（超效率）-SBM模型分析测算的效率值基础上，我们通过计算17个中心城市的轨道交通2013-2015年的序列参比Malmquist指数，估算出2013-2014年、2014-2015年两个时期的全要素生产率变化；进一步地，我们对指数进行分解，计算出每年较上一年的效率变化和技术变化。测算与分解结果如表5所示：

表5：中心城市2013-2015年轨道交通Malmquist指数及指数分解结果

从表5报告的结果可以看出：在2013-2014年，只有天津、沈阳、哈尔滨、上海、重庆、西安6个城市的轨道交通Malmquist指数值大于1，其余11个城市的指数值小于1，这表明上述6个城市的轨道交通全要素生产率有所上升，其余11市的全要素生产率下降，上升（下降）的幅度是指数值减1。17个中心城市的全要素生产率变化差异较大，在全要素生产率上升的城市中，西安市的全要素生产率上升幅度接近翻番；在全要素生产率下降的城市中，杭州、昆明、大连三市的全要素生产率下降的幅度超过50%。2014-2015年的情况较2013-2014年有所逆转：13个城市的轨道交通Malmquist指数值大于1，指数值小于1的城市只有4个，分别是天津、哈尔滨、广州、成都；17个城市的全要素生产率变化差异也较2013-2014年有所收窄。

根据表5报告的Malmquist指数分解情况来看，2013-2015年所有城市的技术变化都大于1，即都呈现技术进步的状态，这是序列参比Malmquist指数的技术特征所决定的。各城市间技术变化的差异不大，各城市Malmquist指数的差异主要源于效率变化的差异，以2013-2014年杭州、昆明、大连三个全要素生产率下降的幅度超过50%的城市为例，其效率变化更是分别达到了-56.74%、-75.17%、-69.50%。对于这三个极端的效率变化，杭州、昆明的情况是由于2014年突然降低的DEA效率评分导致的，但是大连2013年与2014年的SE-SBM评分差异并不大，却出现了效率的大幅降低，这有待进一步解释。

（二）序列参比Malmquist指数与相邻参比Malmquist指数的比较

上节运用序列参比法得出的我国17个中心城市轨道交通的Malmquist全要素生产率指数出现了明显的且无法解释的极端值（2013-2014年大连的指数值），为了检验上文评价结果的可靠性或改进上文Malmquist指数的测算方法，我们又采用了Färe等学者的相邻参比法重新测算、分解了Malmquist指数[20]，并将其结果与序列参比法的结果进行了对比，具体结果如表6所示：

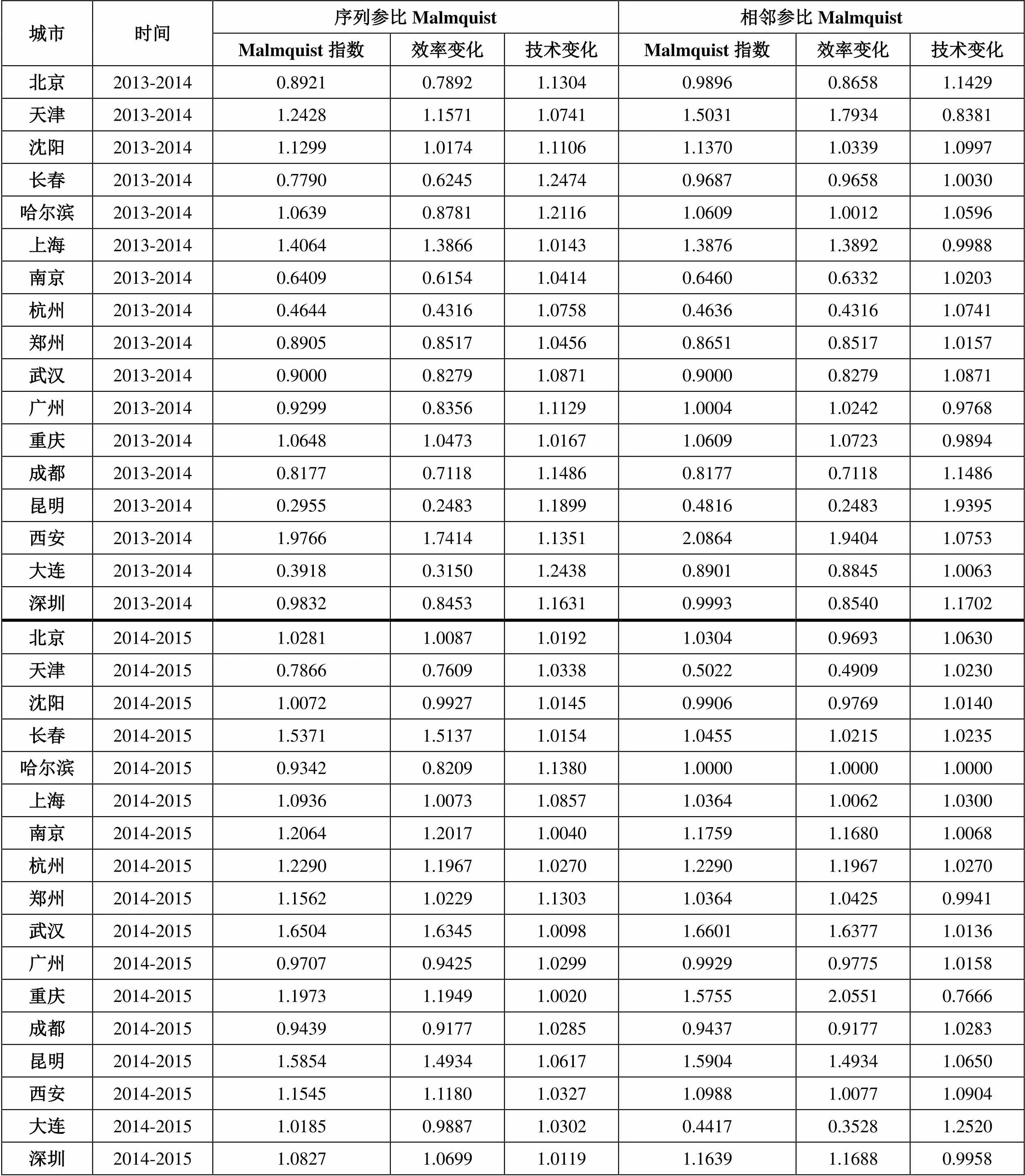
表6：序列参比Malmquist指数与相邻参比Malmquist指数的结果比较

从表6报告的结果可以看出，相邻参比的Malmquist指数可以去除无法解释的极端值，并且对已有的极端值有着较好的解释。如2013-2014年大连的Malmquist指数值在相邻参比法下为0.8901，远高于序列参比法下的0.3918，消除了极端值，改善了测算结果，使其分解的效率变化值能够与SE-SBM效率值相对应。再如2014-2015年重庆的Malmquist指数为1.5755，分解的效率变化为2.0551，尽管效率变化出现翻倍的极端情形，但是我们在DEA评价的效率值上可以得到印证：重庆2014年的SE-SBM效率值仅为0.4906，2015年却大幅攀升至1.0082，后者正好为前者的2.055倍。

但是，相邻参比法测算的Malmquist指数在分解之后技术变化有小于1的情况出现，即有“技术退步”的情形出现，这是一个在理论上不好解释的问题。为了避免技术退步在理论上的难题，序列参比法通过扩大参考集的技术手段，使本期的参考集完全包含了上期的参考集，使得两期效率对比的对象彼此并不独立，有效性存疑。由此可见，两种方法各有利弊，但是我们认为，相邻参比法更适用于轨道交通的Malmquist指数测算：一方面是由其在参考集上的独立性使其在评价的有效性上优于序列参比法，在极端值的处理方面，此优势已得到充分体现；另一方面对于轨道交通行业，技术并不一定总呈现“进步”的状态，它所呈现出的技术效率有时候由外部需求来决定。

六、结论

本文通过运用SBM-Malmquist方法对我国17个中心城市的轨道交通效率进行评价与比较研究，得出以下四点研究结果：第一，通过应用超效率SBM模型，本文对我国17个中心城市的轨道交通效率进行了评价并得出了各城市轨道交通建设运营的相对效率值、排名和松弛改进值。第二，本文通过投入导向的超效率BCC模型对超效率SBM模型结果的进行了检验与比较，检验比较结果显示超效率SBM模型得出的排名是稳健可靠的。第三，在超效率SBM模型的效率值基础上，本文应用序列参比法计算出了17个中心城市轨道交通的Malmquist全要素生产指数，并对其进行了指数分解，得出了每个城市的效率变化与技术变化。第四，本文通过使用相邻参比法对Malmquist指数进行了计算，将相邻参比法的结果与序列参比法的结果进行了比较，比较结果显示相邻参比Malmquist指数更适用于测评城市轨道交通业。

[1] SEIFORD L M,THRALL R M.Recent developments in DEA:The mathematical programming approach to frontier analysis[J].Journal of Econometrics,1990,46(1-2):7-38.

[2] BARNUM D T,MCNEIL S,HART J,et al.Comparing the Efficiency of Public Transportation Subunits Using Data Envelopment Analysis[J].Journal of Public Transportation,2007,10(2):1-16.

[3] MICHAELIDES P G,BELEGRI-ROBOLI A,MARINOS T.Evaluating the Technical Efficiency of Trolley Buses in Athens,Greece[J].Journal of Public Transportation,2010,13(4):93-109.

[4] O VAIDYA.Evaluating the Performance of Public Urban Transportation Systems in India[J].Journal of Public Transportation,2014,17(4):174-191.

[5] WANKE P,BARROS C P,FIGUEIREDO O.Efficiency and productive slacks in urban transportation modes:A two-stage SDEA-Beta Regression approach[J].Utilities Policy,2016,41:31-39.

[6] 王亚华,吴凡,王争.交通行业生产率变动的Bootstrap-Malmquist指数分析(1980-2005)[J].经济学,2008,7(3):891-912.

[7] 王欢明,诸大建.我国城市公交服务治理模式与运营效率研究——以长三角城市群公交服务为例[J].公共管理学报,2011(2):52-62.

[8] 王海燕,于荣,郑继媛,等.DEA-Gini准则在城市公共交通企业绩效评价中的应用[J].系统工程理论与实践,2012,32(5):1083-1090.

[9] 李学文,徐丽群.超效率Gini方法在城市交通行业面板数据中的研究[J].中国管理科学,2014(s1):1-7.

[10] 章玉,黄承锋,许茂增.中国城市公共交通的效率研究_基于三阶段DEA模型的分析[J].交通运输系统工程与信息,2016,16(1):32-37.

[11] SWAMI M.Comparative Appraisal of Metro Stations in Delhi Using Data Envelopment Analysis in a Multimodal Context[J].Journal of Public Transportation,2015,18(3):2062-2064.

[12] 周强,秦菲菲,吴戈.基于DEA方法的城市轨道交通系统效率评价研究[J].铁道运输与经济,2014,36(2):79-83.

[13] 李磊,姚璇宇.基于DEA和Malmquist指数的城市轨道交通行业效率[J].江南大学学报(自然科学版),2015,14(1):103-109.

[14] CHARNES A,COOPER W W,RHODES E.Measuring the efficiency of decision making units[J].European Journal of Operational Research,1978,2(6):429-444.

[15] BANKER R D,CHARNES A,COOPER W W.Some Models for Estimating Technical and Scale Inefficiencies in Data Envelopment Analysis[J].Management Science,1984,30(9):1078-1092.

[16] ANDERSEN P, PETERSEN N C.A Procedure for Ranking Efficient Units in Data Envelopment Analysis[J].Management Science,1993,39(10):1261-1264.

[17] TONE K.A slacks-based measure of super-efficiency in data envelopment analysis[J].European Journal of Operational Research,2002,143(1):32-41.

[18] MALMQUIST S.Index numbers and indifference surfaces[J].Trabajos de Estadistica Y de Investigacion Operativa, 1953, 4(2):209-242.

[19] CAVES D W,CHRISTENSEN L R,DIEWERT W E.Multilateral Comparisons of Output,Input,and Productivity Using Superlative Index Numbers[J].Economic Journal,1982,92(365):73-86.

[20] R. FÄRE,S. GROSSKOPF,B. LINDGREN,et al.Productivity Changes in Swedish Pharamacies 1980-1989:A Non-Parametric Malmquist Approach[J].Journal of Productivity Analysis,1992,3(1):85-101.

[21] SHESTALOVA V.Sequential Malmquist Indices of Productivity Growth:An Application to OECD Industrial Activities[J].Journal of Productivity Analysis,2003,19(2):211-226.

[22] SEIFORD L M,ZHU J.Infeasibility Of Super-Efficiency Data Envelopment Analysis Models[J].Infor Information Systems & Operational Research,1999,37(2):174-187.

本文推荐专家：

姚波，西安财经学院，教授，研究方向：经济统计学。

杨松，北京市社会科学院,副研究员，研究方向：城市经济学。

A Comparative Analysis of Urban Rail Transit Efficiency Based on Super Efficiency SBM-Malmquist Approach

ZHENG YOUYUAN1, LIU YANPING2, HE YAN3

In this paper, Super Efficiency SBM model has been applied to evaluate the relative efficiency 17 central cities of China. The relative efficiency score, ranking, and the slack movement have been measured. In order to test the robustness of the evaluation results, the evaluation results of Super Efficiency BCC model have been used to compare with the results of Super Efficiency SBM model, the comparison results show that the results of super efficiency SBM model are robust and reliable. Based on efficiency score of Super Efficiency SBM model, the Sequential Malmquist Indexes have been measured and compared with the Adjacent Malmquist Indexes, the comparison results show that the Adjacent Malmquist Index is more applicable to evaluate urban rail transit industry.

Super Efficiency SBM Model; Malmquist Index; Urban Rail Transit Efficiency; Sequential Comparison Approach; Adjacent Comparison Approach

F570

A

1008-472X(2018)01-0023-12

2018-03-06

陕西省软科学2016年度重点项目“扩大城市交通容量与典型城市范例研究——以西安市为例”（2016KRZ005）

郑又源（1985-），男，甘肃兰州人，博士研究生，西安电子科技大学经济与管理学院讲师，研究方向：交通经济学；刘延平（1962-），男，辽宁沈阳人，博士研究生，教授，博士生导师，中国传媒大学党委常委、副校长，研究方向：交通经济学。