某铁路客站站房及雨棚风洞试验研究及分析

高 涛

(中铁第一勘察设计院集团有限公司,西安 710043)

随着我国铁路客运专线、城际铁路的快速发展，出现了越来越多的大跨度铁路客站站房及雨棚，与传统铁路站房相比，其具有自重轻、竖向周期偏大、阻尼较小等显著特点[1]，属于风荷载敏感结构，因此风荷载对结构的脉动作用是不可忽略的[2]。由于站房及雨棚的复杂性和唯一性，不同造型的结构具有自身特定的规律性，如女儿墙的高度、屋面坡度、檐口悬挑长度、雨棚与站房相对位置等，对风荷载的取值和受力特征都有较大的影响。但是，现行的《建筑结构荷载规范》(GB50009—2012)中并没有给出对此类结构的抗风设计规定，也没有风振系数的经验数据及计算公式[3]。而准确合理的风荷载取值对确保结构安全、控制工程造价都显得十分重要[4]，所以对大型客站站房及雨棚进行风洞试验研究和分析是非常有必要的。

风洞试验是研究复杂工程中结构风的有效方法，在军工及大型体育馆建筑中已有很多研究成果[5]。从浙江大学对杭州市铁路新客站进行风洞试验研究开始，我国对铁路客站及雨棚的风洞试验研究逐步发展并成熟。如哈尔滨西客站站房采用多目标等效风荷载分析方法[6]，得出该方法与动力极值方法的一致性。武汉客站站房屋盖和雨棚采用压力方差的统计学方法[7]，得出吊顶镂空与封闭的情况基本一致的结论。本文以某铁路大型客站站房及雨棚为对象，通过风洞试验给出建筑表面的平均压力系数，在此基础上通过有限元风致振动分析，得到屋面各部分的风振系数，计算不同风向下的等效静风荷载，以用于主体结构设计[8]。大型铁路客站站房及雨棚鸟瞰图如图1所示。

图1 大型铁路客站站房及雨棚鸟瞰

1 风洞试验

1.1 试验模型

本试验选取刚性模型作为试验对象，模型由ABS板和有机玻璃构成，因此模型的刚度和强度均符合试验要求。为了符合风洞阻塞率的几何要求，同时考虑试验台的容量，试验模型的几何比例取为1∶200[9]，如图2所示。

图2 站房及雨棚模型外观

试验共布置593个测点，其中站房屋面上测点位222个，由于雨棚上、下表面均受风荷载作用，故在雨棚上、下表面分别布设测点，其上表面布设测点位244个，其下表面测点位127个。将1.2 mm×0.1 mm的不锈钢管埋设在预先设计好的各个测点处，不锈钢管长度方向与建筑物外表面垂直，且不能突出外表面，保证上表面与模型外表面处于同一平面，与实际环境一致。试验前对每个不锈钢测压管检测，测压孔全部有效。风洞流场利用粗糙元、挡板、尖塔等扰流装置进行模拟B类场地。通过测量风速设备，经过反复调试，满足力学相似的要求，可以得到可靠的试验测量值[10]。

1.2 平均风压系数

平均风压系数为体型系数与高度变化系数的乘积，为无量纲值。结合风致振动分析，通过刚性模型测压风洞试验，可确定建筑表面的平均压力系数，为主体结构设计提供重要的数值依据。限于篇幅，本文仅给出站房和雨棚各一风向角下的平均风压系数分布图。图3为270°风向角下站房屋面的平均风压系数分布；图4为195°风向角下雨棚的平均风压系数分布。

图3 站房屋面风压系数分布

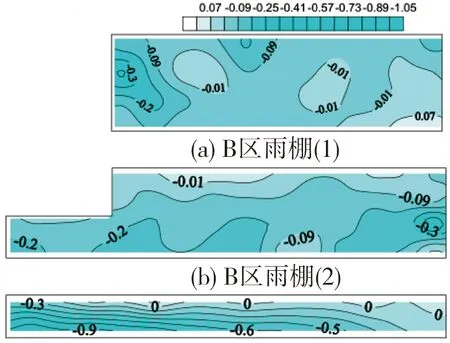
图4 雨棚屋面风压系数分布

2 有限元风致振动分析

2.1 有限元模型

采用通用有限元分析软件Ansys进行了站房和雨棚结构的风振反应分析，站房和雨棚的整体有限元模型如图5所示，为了提高计算效率，将站房和雨棚分开分别进行计算分析。

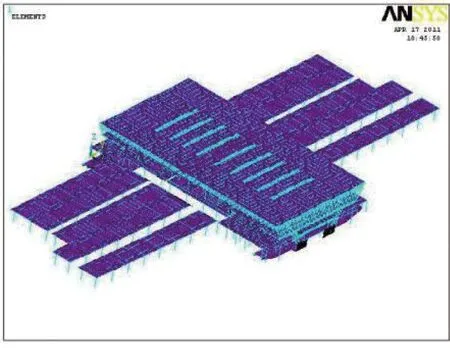
图5 站房及雨棚整体计算模型

站房结构有限元模型共25 136个单元、10 614个节点，主要采用了梁单元Beam44和壳单元Shell63，其中20 445个梁单元主要模拟屋面钢网壳以及混凝土梁柱构件，4 691个壳单元用来模拟屋面板及混凝土楼板；雨棚结构模型共1 620个单元、641个节点，亦采用梁单元Beam44和壳单元Shell63。雨棚沿纵向分为3个独立的结构单元，考虑到每部分节点不多，将雨棚3部分一起进行计算。

2.2 自振特性分析

自振频率是分析结构动力响应的重要参数，故先对结构的自振特性进行分析，再进行结构风致振动响应分析。利用有限元软件进行动力响应的分析，可以得到结构各振型参与振动的水平，选出对振动参与最大的几个振型。本文采用Ansys[11]有限元软件分别对站房及雨棚进行自振特性分析。

站房前7阶自振频率的情况如表1所示，基频为1.17 Hz，可以看出该结构形式属于频率密集型结构。图6给出了站房的第1、第2阶结构振型。

表1 站房自振频率

图6 站房振型

根据各振型可以看到，结构的第1阶振型主要表现为整体的水平振动，而并非屋盖网架结构竖向振动，原因是该结构的水平向刚度较弱。总体来看结构水平刚度较弱而竖向刚度较强。

雨棚前7阶自振频率的分布情况如表2所示，结构基频为1.29 Hz，属典型的频率密集型结构。图7给出了雨棚的第1、第2阶结构振型。

表2 雨棚自振频率

图7 雨棚振型

根据各振型可以看到，雨棚的前两个阶振型主要表现为整体水平振动，而并非屋盖结构竖向振动，这主要是雨棚柱子刚度较弱而屋盖整体刚度较好。

2.3 风振响应分析方法

本文采用了非线性时程分析法对该屋盖结构进行风振响应分析，时程分析法是通过有限元法实现结构离散化，然后在相应的各单元节点上进行风荷载作用，通过在时间域内解运动方程从而得到结构的响应[12]。理论上讲，这种方法可推广到任何系统以及任意激励，而且能够求得比较完整的结构动力响应的全过程信息。因此，这种方法成为分析处理大跨屋盖结构风振响应的有效手段。

根据本工程的特点，最终确定风振系数的计算方法是直接基于结构响应的位移风振系数和内力风振系数，其表达式如下[13]

(1)

(2)

其中，Dy为符号函数；σy为脉动风响应均方差；g为峰值因子，其大小与1 h平均时间内穿越荷载效应平均值的次数有关，当平均荷载效应的概率分布为正态分布时，g可按式(3)计算，其中T为观察时间(通常为1 h)，v为水平跨越数，其常用范围在3.0～4.0，这里取为3.5[13]。

(3)

风振系数的计算采用公式(1)即可求得结构中每根杆件内力风振系数和各个点内力位移风振系数。

2.4 风振响应分析研究

前述风洞试验共进行了24个风向的风试验，通过结果分析，取出风作用影响较大的几组风向角作为风振响应分析的工况，各方向角如下。

站房：0°、75°、90°、180°、270°；

雨棚：0°、195°、210°、330°。

结合大跨屋盖结构的特点和设计人员所关心的风振响应，本文以节点竖向位移和杆件应力作为风振响应指标[14]。限于篇幅，本文仅给出站房270°风向角和雨棚195°风向角下的具体计算结果。

站房屋盖结构节点竖向位移分布云图如图8所示，从图8可以看出，屋盖中部位移较周边位移偏大，其原因是屋盖跨中位置距框架柱的距离较远，竖向约束较弱，竖向刚度较弱，所以最大位移出现在屋盖中部跨中位置处。图9给出了内力屋盖结构受力最大的杆件单元的位置，该靠近屋面网架支座处，所以设计中建议加强屋面网架支座处杆件的构造措施。

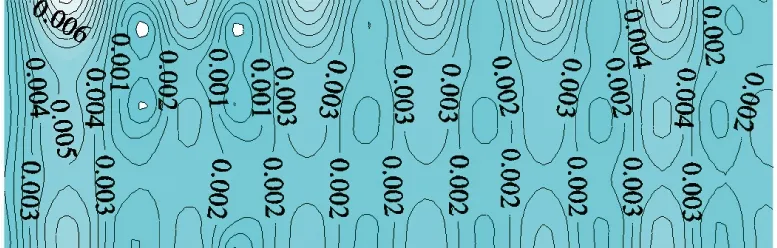
图8 站房屋面极值位移分布(单位:m)

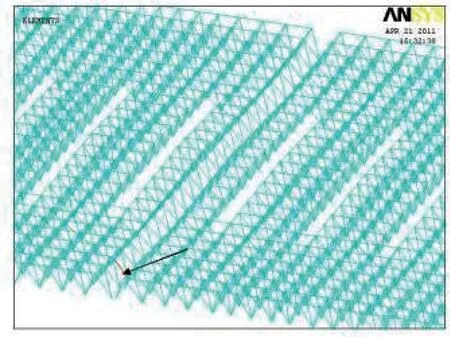
图9 站房屋面最大内力杆位置

图10 雨棚极值位移分布云图(单位:m)

图10给出了雨棚节点最大位移分布云图，可以看出边缘位移较大，其原因是该位置支承条件较弱。雨棚最大位移节点和最大内力杆位置如图11所示，可看出雨棚整体结构薄弱点位于雨棚边跨的斜支撑杆处。

图11 雨棚最大内力杆位置

根据时程分析和统计方法，确定结构在各最不利风向角下的极值响应及对应的整体风振系数见表3、表4。

表3 各风向角下站房屋面结构极值响应及风振系数

表4 各风向角下雨棚结构极值响应及风振系数

从表3可以看出，对于站房屋面结构，风振最大位移为3.34 cm，发生在180°风向角，最大内力为174.34 MPa，发生在270°风向角，结合位移和内力两个因素考虑，270°为站房最不利风向角。从表4可以看到，雨棚风振最大位移为2.57 cm，最大内力为89.08 MPa，均发生在195°风向角下，195°为雨棚最不利风向角。

3 等效静风荷载

等效静风荷载是根据由风洞试验得到平均压力系数，乘以由有限元分析得到的风振系数，再乘当地的基本风压得到，其可作为标准值直接用于主体结构的设计。站房及雨棚屋面的等效静风荷载如图12、图13所示。

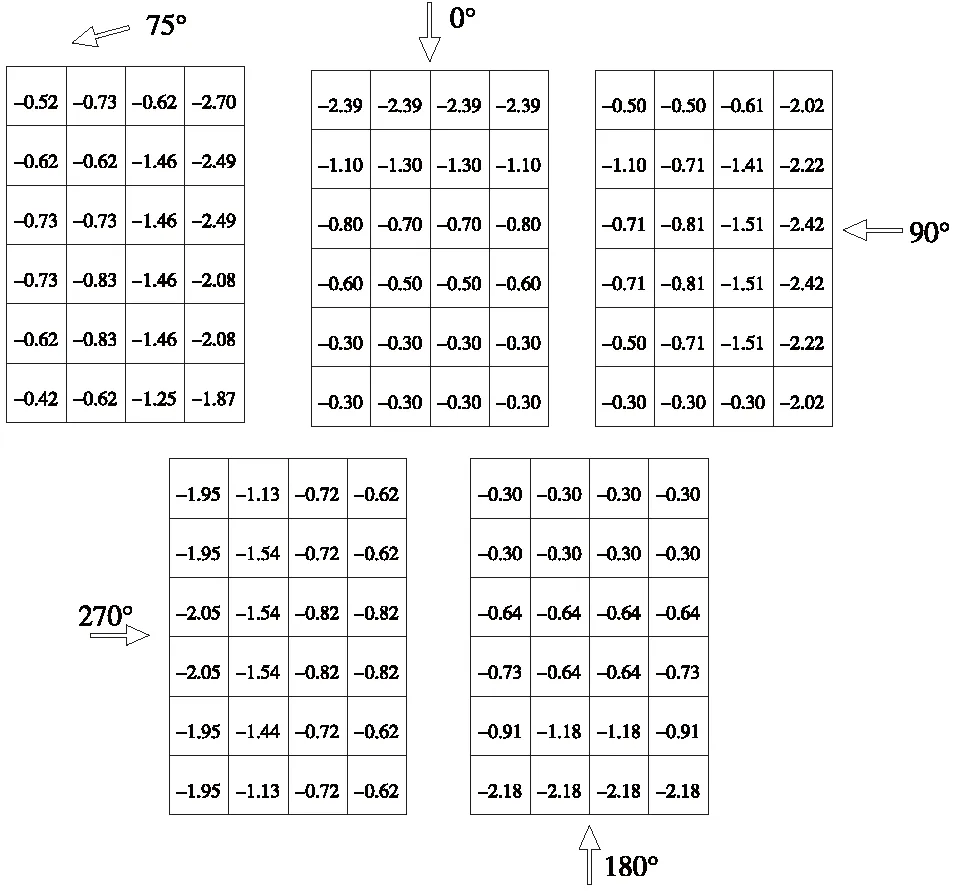
图12 站房屋面等效静风荷载

图13 雨棚等效静风荷载

从图12可以看出，顺风向站房屋面的风荷载值衰减比较明显，较现行《建筑结构荷载规范》中规定的单一风荷载取值更为合理。特别是对于大跨度屋面，合理分段选用风荷载值，对屋面构件的设计影响较大，关系到结构设计的安全性和经济性；从图13可以看出，雨棚屋面风荷载值亦为顺风向递减明显，但由于受站房的影响，雨棚屋面在靠近站房附近一定范围内形成高压旋涡，局部风荷载较大，设计时应引起重视。总体来看，站房及雨棚屋面风荷载最大值一般出现在结构的外侧边缘地带，主体结构及屋面围护设计时应采取加强措施[15]。

《建筑结构荷载规范》及文献[16]对四面开敞结构中提出体系系数要考虑变号，即雨棚屋面可能出现正风压，而在本试验中风荷载并未出现正风压，与所采用的模型刚度和体型有一定的关系。建议在实际设计中，应根据雪荷载等其他屋面活荷载的大小，适当考虑正风压的作用。

4 结论与设计建议

(1)结合模型风洞试验及有限元风致振动分析，得出了站房和雨棚在不利风向角下的风振系数和等效静风荷载，可直接用于主体结构设计。

(2)在脉动风荷载作用下，站房屋面跨中最大位移为3.34 cm(向上)，发生在270°风向角下；雨棚屋面最大位移为2.57 cm(向上)，发生在195°风向角下。最大位移均发生在迎风侧的屋面边缘处，与屋面最大等效静风荷载值位置基本一致，因此应加强边缘处主体结构及围护构件的设计。

(3)对于站房和雨棚屋面风荷载，其值均顺风向递减，因此设计中可对屋面结构风荷载进行分区段取值，以确保结构设计的安全性和经济性。

(4)建议在雨棚结构设计时，根据雪荷载等其他屋面活荷载的大小，适当考虑正风压的作用。

[1] 刘丹，黄本才，史益军.复杂双侧大悬挑屋盖平均风压数值模拟[J].计算机辅助工程，2007，16(3)：38-42.

[2] 尧国皇，谭伟，张进军，等.惠阳体育会展中心上部钢结构设计[J].钢结构，2009，24(4)：32-37

[3] 中华人民共和国住房和城乡建设部.GB50009—2012 建筑结构荷载规范[S].北京：中国建筑工业出版社，2012.

[4] 韩志伟.铁路客站大型复杂结构健康监测研究与思考[J].铁道经济研究，2011(6)：28-32.

[5] 肖勇.青岛新火车站主站房风洞实验研究[D].成都：西南交通大学，2001：4-5.

[6] 吴迪，武岳，孙瑛，等.大跨度铁路站房屋盖结构风洞试验与等效静风荷载研究[J].建筑结构学报，2012，33(1)：43-50.

[7] 陈凯，何连华，符龙彪.武汉火车站站房屋盖和雨棚风洞试验研究[J].建筑结构，2009(1)：16-19.

[8] 侯信真.大跨屋盖结构的刚性模型风洞试验研究[D].南京：东南大学，2009：10-11.

[9] 彭留留，黄国庆，李明水，等.某机场新航站楼风压分布特征及风振系数研究[J].空气动力学学报，2015，33(4)：572-579.

[10] 杨丽.风洞实验及其在建筑领域应用的研究[J].建筑科学，2011(S2)：117-122.

[11] 江见鲸，陆新征，叶列平.混凝土结构有限元分析[M].北京：清华大学出版社，2006：20-30，50-63.

[12] 赵雪峥，郑阿妮，隋庆海.深圳大运中心体育馆风洞试验结果分析与研究[J].建筑结构，2011，41(4)：109-112.

[13] 史益军，黄本才，刘丹.体育馆大跨屋盖空间风振分析[J].计算机辅助工程，2008，17(1)：21-24.

[14] 毕磊，刘松华，任志彬，等.天津海河教育园区体育中心风洞试验研究及应用[J].建筑结构，2013(S1)：977-981.

[15] 朱晓华，高敏杰.中美屋面系统抗风揭对比试验及结果分析[J].中国建筑防水，2011(19)：6-12.

[16] 温四清，董卫国，邱剑.铁路客站站台雨棚风荷载计算探讨[J].铁道经济研究，2012(5)：55-59.