重力式挡土墙列车荷载侧压力计算

周 坤

(中铁工程设计咨询集团有限公司,北京 100055)

1 概述

对于重力式挡土墙后路基面作用均布荷载的情况，铁路行业传统上是将荷载简化为一定高度、宽度的土柱与墙背土体一同按库伦理论或朗肯理论求解荷载引起的侧压力[1-2]。在容许应力设计法的条件下，这种处理简便易行，给予设计人员极大的便利。

目前铁路行业正逐步推行极限状态设计法，相关设计规范也在修订、完善中。2016版《铁路路基设计规范》[3]以及正在修订中的《铁路路基支挡结构设计规范》均将轨道荷载、列车荷载分列，并按均布荷载给出，其中轨道荷载为永久作用，列车荷载为可变作用。而永久荷载、可变荷载在不同荷载组合中的作用效应值是不同的，因此有必要对其侧压力计算方法进行讨论。

2 常用的均布荷载侧压力计算方法

常用的均布荷载侧压力计算方法主要分经典理论、弹性理论两种。

2.1 经典库伦理论

一般来说重力式挡土墙墙背承受主动土压力。库伦理论认为[4-5]，当墙后土体开始滑动时，处于极限平衡状态，破裂棱体在其自重W(含破裂面以内荷载)、墙背反力Ea(其反作用力即为土压力)和破裂面反力R的作用下维持静力平衡。Ea与墙背法线成δ角(墙背与土体间摩擦角)，R与破裂面法线成φ角(土体之间摩擦角)，并均偏向阻止滑动一侧。如图1所示。

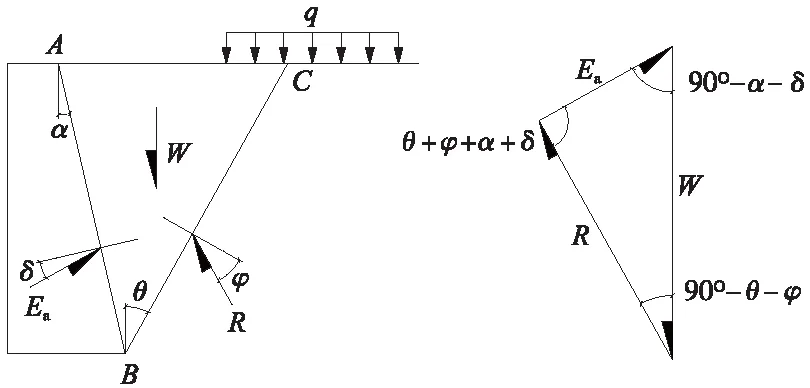
图1 库伦理论计算路基面荷载侧压力图示

主动土压力按式(1)计算，荷载q引起的侧压力包含在Ea中。

(1)

不考虑出现第二破裂面的情况，经W的重心作破裂面的平行线，该平行线与墙背交点即为Ea合力的作用点。土体与荷载各自产生的侧压力按其在W中所占比例确定，作用点按通过各自重心平行于破裂面的直线确定。很明显，q的分布宽度及位置不同、荷载集度不同，W、Ea、R的平衡关系就不同，相应的破裂面也不同。如果路基面作用多个分布荷载，分布宽度不同，既有永久作用又有可变作用，其荷载组合引起的侧压力计算将非常复杂。铁路挡土墙为简化设计，将土体、路基面荷载引起的侧压力按综合作用效应参与组合，采用了相同的分项系数[6-7]，这与作用分类、荷载分项系数的概念不协调，也易引起设计者概念上的误解。

德国规范对路基面轨道结构及列车荷载产生的侧压力计算如图2所示[8-9]。

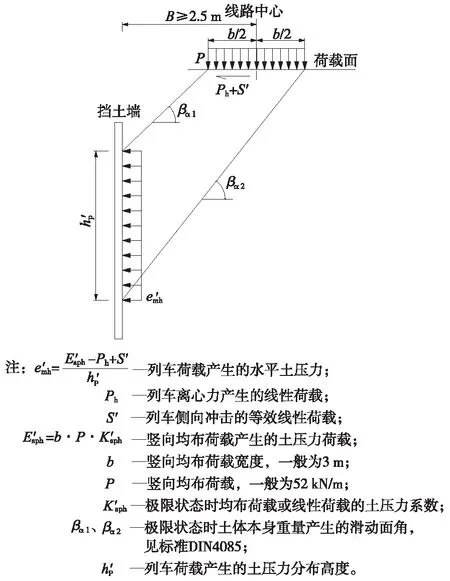
图2 德国铁路支挡结构路基面荷载侧压力计算图示

这种侧压力与土体本身重力产生的土压力无关，只与其破裂角相关，而不同墙高处的破裂角是唯一的，轨道荷载、列车荷载产生的侧压力也是唯一的，按此可以进行不同的荷载组合，考虑不同的分项系数，方法明确、概念清晰，值得我国铁路设计人员借鉴。

2.2 经典朗肯理论

朗肯主动土压力计算时，剪切破坏面与竖直面的夹角为固定值45°-φ/2，主动土压力按式(2)计算，主动土压力系数Ka按式(3)计算。路基面荷载产生的侧压力计算如图3所示。这种侧压力与土体本身重力产生的土压力无关，是唯一的，可以进行不同的荷载组合，考虑不同的分项系数。我国住建部建筑基坑支护技术规程[10]及边坡工程技术规范[11]即推荐图3所示的计算方法计算基坑支护结构上的土压力。

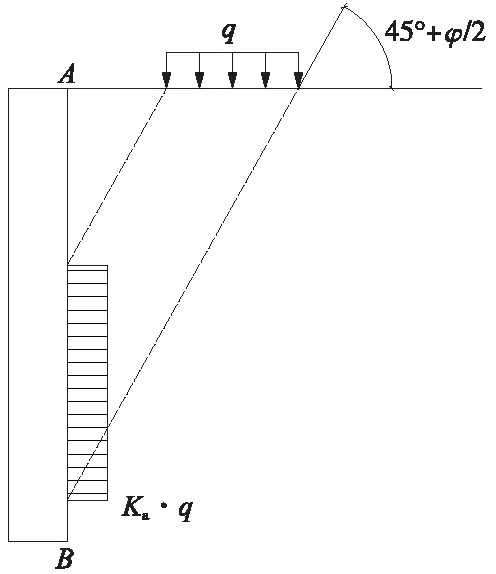
图3 基坑规程推荐的计算方法

(2)

Ka=tan2(45°-φ/2)

(3)

由于朗肯理论基于墙为刚体、墙背垂直且与填土之间无摩擦力、墙背填土面水平等假定条件，局限性较大，因此铁路较少应用。

2.3 弹性理论

弹性理论侧压力计算如图4所示(图中C为q的作用中点)，其侧压力与地层的物理力学性质无关，适用于墙背地层相对均匀的情况[12]。墙背地层性质差别较大时，可按弹性模量换算当量厚度进行均一化处理[13]。

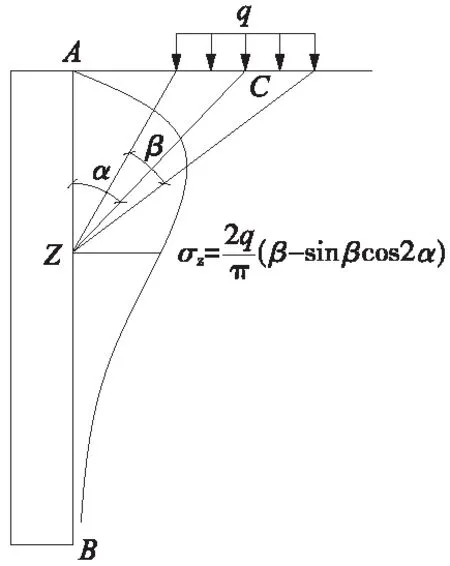
图4 弹性理论计算侧压力

弹性理论计算过程繁琐，加之很多研究人员及学者认为其没有考虑土的抗剪强度对主动土压力的影响，铁路此前应用较少。目前铁路规范在桩支挡、直墙类支挡中推荐了该计算方法。

3 关于荷载引起侧压力的讨论

目前铁路填方挡土墙一般不高于8 m。多数研究及实测结果认为：对于路肩挡土墙，列车荷载引起的侧压力合力基本作用在0.5倍墙高处[14-18]。山西中南部铁路5 m高路肩挡土墙实测30 t轴重C96单线列车侧压力与同条件下弹性理论计算值、有限元模拟计算值对比如图5所示。其合力及作用点位置见表1、表2。

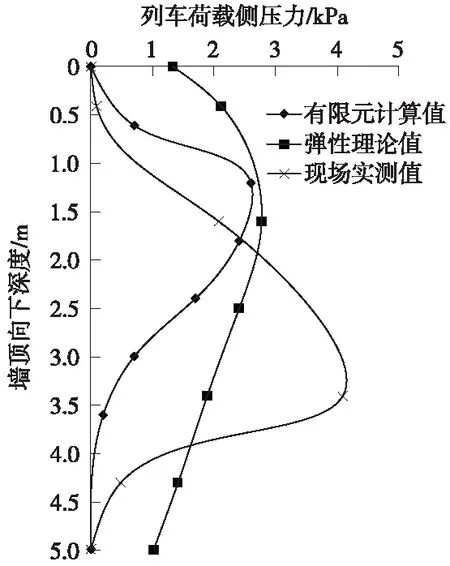
图5 计算列车荷载侧压力与实测数值对比

实测弹性理论有限元9.110.25.1

表2 侧压力合力作用点位置(距墙底)与倾覆力矩

注：H为墙高。

(1)列车荷载侧压力不利于抗倾覆稳定

一般来说，库伦理论计算土体对路肩挡土墙墙背侧压力合力作用点位于距墙趾1/3墙高处，表2中列车荷载引起的侧压力合力作用点明显高于1/3墙高，因此列车荷载侧压力对抗倾覆稳定更不利[19]。

(2)规范提出的荷载分布宽度偏小

对前述实测工点，取墙高5～8 m，墙后填土容重20 kN/m3，综合内摩擦角40°，墙背与填土之间的摩擦角取20°，路基面半宽4.05 m，线间距4 m，轨道及30 t轴重列车荷载按现行重载铁路设计规范[20]分别取17.6、56.4 kPa，荷载分布宽度3.4 m，对比库伦理论、弹性理论计算的土体、轨道荷载、列车荷载共同作用产生的侧压力，结果见表3。

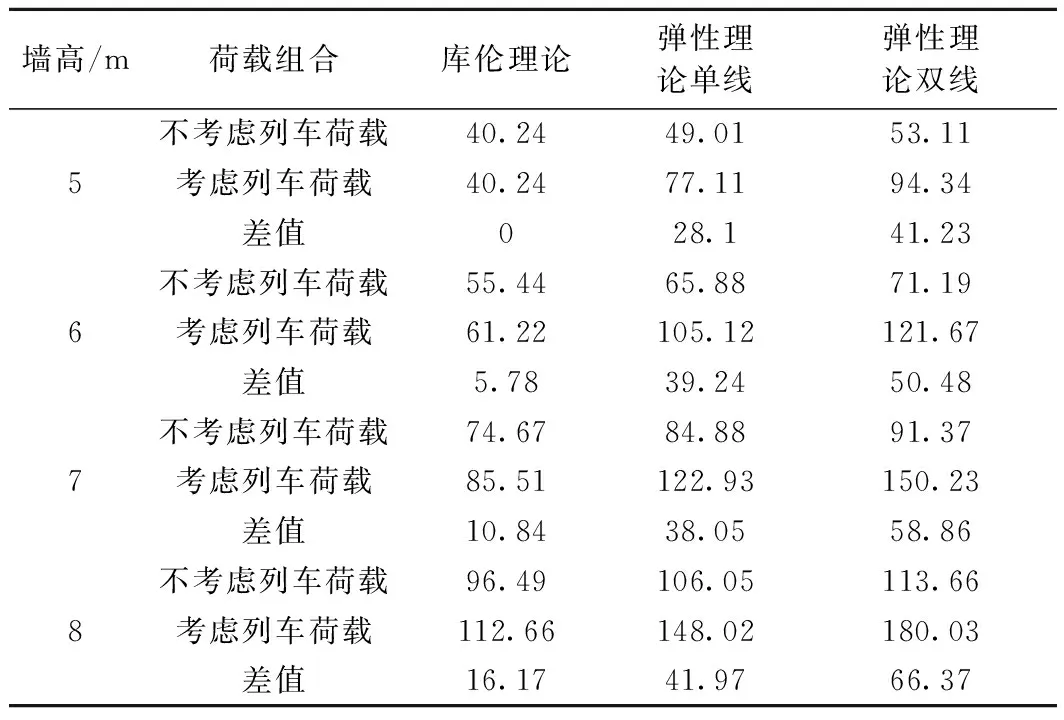
表3 库伦理论与弹性理论土压力结果对比 kN

很明显，弹性理论求得的数值比库伦理论大。原因是库伦理论仅破裂面内的轨道及列车荷载对挡墙侧压力有贡献，而弹性理论计算时轨道及列车荷载可以作用到墙体的任意位置；另外，实测、有限元模拟、弹性理论计算均显示列车荷载侧压力沿墙高均有分布，而本例按库伦理论计算墙高大于5.8 m时破裂面才能交于荷载内，也就是说墙高小于5.8 m时轨道及列车荷载对挡土墙侧压力无影响。基于以上分析，笔者认为规范给出的荷载分布宽度偏小。

(3)弹性理论计算的荷载侧压力分布图形与实测、有限元模拟类似，库伦理论计算的荷载侧压力分布重心偏低。因此笔者认为采用弹性理论计算侧压力更符合实际情况。

4 结论

针对列车荷载对填方重力式挡土墙的侧压力分布，本文通过对比分析不同理论计算结果、有限元模拟计算结果、现场实测结果，结合极限状态法设计需求，得出如下结论。

(1)列车荷载侧压力合力作用点高于土体侧压力合力作用点，列车荷载侧压力对抗倾覆稳定不利。

(2)采用弹性理论，荷载侧压力分布图形更接近实际状态，易于引入不同分项系数进行荷载组合。弹性理论计算侧压力值偏大，建议仅考虑靠近挡土墙侧的单线荷载。

(3)采用库伦理论，宜适当加大荷载分布宽度，减小荷载与挡墙距离，以充分考虑列车荷载影响；引入极限状态法时，建议参照德国规范，列车荷载不影响土体破裂面位置，以便引入不同分项系数进行荷载组合。

[1] 中华人民共和国铁道部.TB 10025—2006/J 127—2006 铁路路基支挡结构设计规范[S].北京：中国铁道出版社，2006.

[2] 铁道部第一勘测设计院.铁路工程设计技术手册·路基[M].修订版.北京：中国铁道出版社，1995.

[3] 国家铁路局.TB 10001—2016/J 447—2016 铁路路基设计规范[S].北京：中国铁道出版社，2017.

[4] 龚晓南.土力学[M].北京：中国建筑工业出版社，2002.

[5] 李广信.土力学[M].4版.北京：清华大学出版社，2014.

[6] 中国铁路总公司.Q/CR 9127—2015 铁路路基极限状态法设计暂行规范[S].北京：中国铁道出版社，2016.

[7] 刘昌清，罗一农，魏永幸.基于极限状态设计法的重力式挡墙设计研究[J].铁道工程学报，2014(9):30-34.

[8] Hartmut Freystein，Martin Muncke，Peter Sehollmeier.德国铁路基础设施设计手册[M].北京：中国铁道出版社，2007.

[9] 刘少飞.重力式支挡结构的荷载图式研究[D].成都：西南交通大学，2010.

[10] 中华人民共和国住房和城乡建设部.JGJ 120—2012/J 1412—2012 建筑基坑支护技术规程[S].北京：中国建筑工业出版社，2012.

[11] 中华人民共和国住房和城乡建设部.GB 50330—2013 建筑边坡工程技术规范[S].北京：中国建筑工业出版社，2014.

[12] 李海光，等.新型支挡结构设计与工程实例[M].2版.北京：人民交通出版社，2011.

[13] 张千里.30 t轴重重载铁路路基关键技术研究[R].北京：中国铁道科学研究院，2012.

[14] 赵勇.高速铁路刚性挡土墙土压力模型试验与数值分析[D].成都：西南交通大学，2006.

[15] 赵勇，龚熙维，朱俭华.列车荷载作用下墙高对重力式挡墙土压力影响[J].路基工程，2007(5)：110-111.

[16] M M Sherif， R D Mackey. Pressures on Retaining Wall with Repeated Loading[J]. Journal of Geotechnical Engineering Division，1977，103(11)：1341-1345.

[17] 李世元.重力式支挡结构列车动荷载试验研究[D].成都：西南交通大学，2010.

[18] 刘运涛，刘少飞，刘昌清.列车荷载对衡重式挡土墙土压力及稳定性影响研究[J].路基工程，2011(2)：27-29.

[19] 罗一农，刘会娟，苏谦.动应力对支挡结构安全性影响的分析：铁路客运专线建设技术交流会论文集[C].武汉：长江出版社，2005.

[20] 国家铁路局.TB 10625—2017/J 2289—2017 重载铁路设计规范[S].北京：中国铁道出版社，2017.