基于混合多属性决策的铁路站位方案评价模型

罗 圆,朱 颖,张小强,姚令侃

(1.中铁二院工程集团有限责任公司,成都 610031； 2.西南交通大学土木工程学院,成都 610031)

铁路选线时车站位置的分布和站址的选择往往影响线路的局部走向，它关系到城市规划、工程投资、运营收入，甚至是周边地区经济发展等一系列主要问题，是一个多层次、多因素、多指标的多目标决策过程[1]。铁路车站的选址和建设，因其牵涉面广、问题复杂、取决因素多而情况各异，故难以找到普遍性的规律，使得目前理论依据及定量方法技术缺乏[2，3]。如果部分车站选址不合理，将降低旅客出行和货物运输效率，甚至导致生态环境和社会等多方面的问题。

传统的铁路选线方案评价和比选，主要是在经济上追求换算工程运营费最省，并对比较方案的工程技术条件、环境影响、社会效益等定性因素进行分析，选出最优方案[4-9]。这种方法在很大程度上要依靠专家的工程实践经验，不仅增加了专家的工作量，而且容易受主观因素的影响。同时，当定量指标和定性指标相互交叉，难以直接确定最优方案时，目前也缺乏相应的综合评价方法。基于此，本文根据铁路选线设计的特点，遵循站位方案比选原则，建立全面的评价指标体系；引入离差最大法计算指标的权重，然后利用三角模糊数对定性指标进行量化；最后使用混合多属性决策方法解决铁路站位方案的定量和定性综合评价和比选问题，进而确定最优站位方案，为实际决策者提供定量化的决策支持和确实可行的依据。

1 铁路站位方案综合评价指标体系

铁路站位方案评价和比选是一个复杂的系统工程，首先需要解决的技术关键是提出方案评价指标，以构建评价指标体系，但由于该方面理论仍处于探索阶段，目前还没有统一的构建标准。通过现场调研和向专家咨询，利用层次分析法的原理，从技术、经济、环境和社会4个宏观层面，选择了桥隧比、工程投资、对生态环境的影响和满足地方需求的能力等定量、定性相结合的指标，建立了如表1所示的铁路站位方案综合评价指标体系，可依据铁路决策设计时站位方案的实际情况作相应选择和调整。

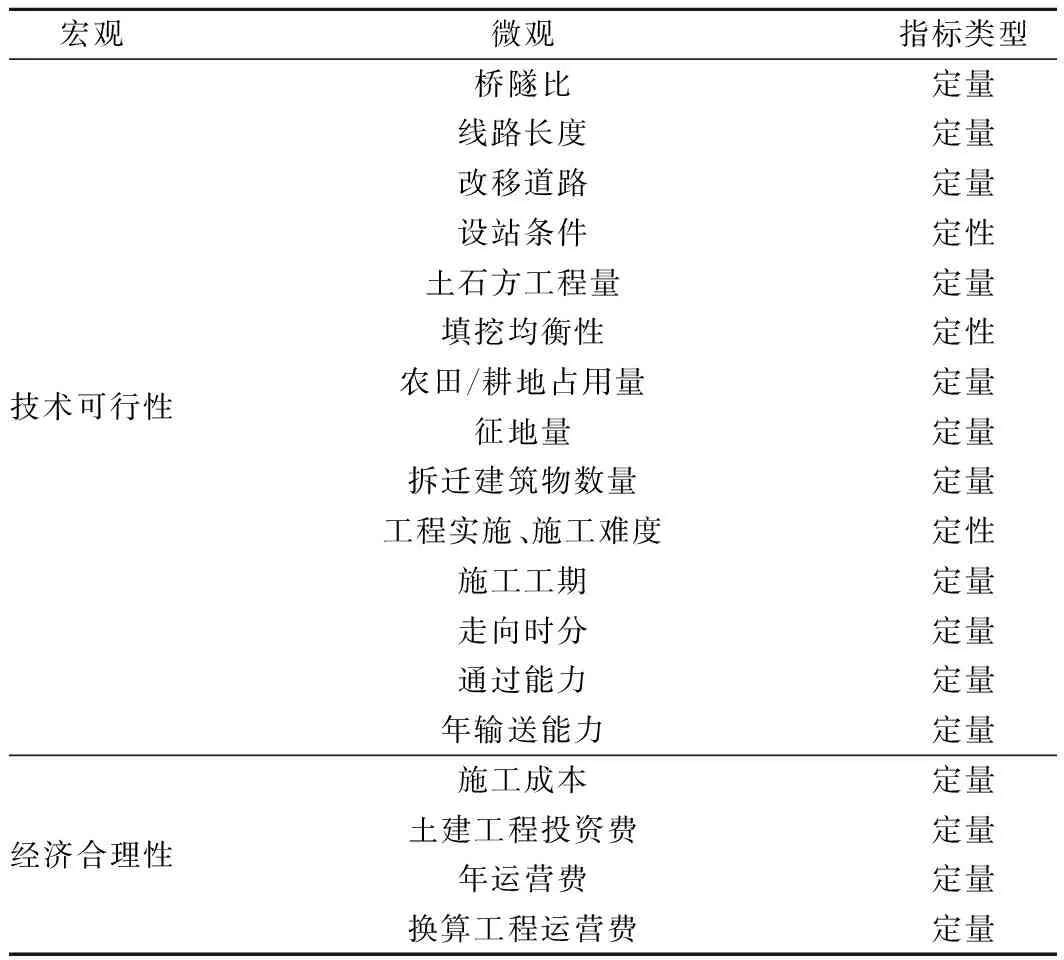
表1 铁路站位方案综合评价指标体系

续表1

2 基于离差最大化的指标权重确定

目前，铁路选线设计的方案比选中广泛采用层次分析法(AHP)，但其计算比较复杂，且需要由专家对指标之间进行相互比较和赋值，当评价指标较多时会成指数倍增加专家的工作量，且计算的指标权重易受专家主观因素的影响。为此，引入离差最大化方法，计算指标的权重。该方法只利用指标取值的差异程度来确定权重，方法原理清晰，计算简单，且避免了主观因素的干扰，能给决策者以最客观的决策支持。

离差最大化法计算指标权重的基本原理为：如果某个指标在所有方案下取值的差异(或距离)越大，则表明该指标对方案比选所产生的影响就越大，那么决策者就应该更加重视该指标，其权重就越大；反之，则表明该指标对方案比选所产生的影响就越小，其权重也相应的就越小。因此，从指标实际取值情况对方案比选能够产生的影响程度方面考虑，不管指标本身在决策者心目中的重要性如何，哪个指标取值的差异程度(即离差)越大，它就应该被赋予越大的权重；而离差越小权重就越小[10-11]。

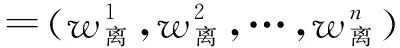
首先，用Dij(W)表示方案Xi与其他方案关于指标Cj取值的偏差，则可定义

并且设

对指标Cj而言，Dj(W)表示所有方案与其他方案的偏差，而指标权重向量W的选择应该使所有指标对所有方案的总偏差最大。所以构造偏差函数

(1)

故，通过求解下面单目标最优化问题就可以求出指标的权重向量W

(2)

通过构造下面的拉格朗日函数，求解式(2)中的最优化问题

分别对wj和δ求偏导，并令其为0，得到

(3)

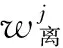
(4)

(5)

将式(5)代入式(4)中，并进行归一化处理后得到

(6)

3 基于混合多属性决策的铁路站位方案综合评价模型

3.1 混合多属性决策

在多属性决策问题中，由于属性有定性和定量之分，决策方案在各指标下的取值有3种情况：全部为定量值，即数字；全部为定性描述，即语言；其数据可以是精确的，也可以是不精确的，如区间数，模糊数等；既有定量值又有定性描述。与这3种情况对应的多属性决策问题分别称为定量型、定性型和混合型多属性决策问题。为了保持定性指标取值信息的模糊性，本文利用三角模糊数对定性指标进行量化，因此，定性指标量化的三角模糊数和定量指标取值的精确实数一起，构成了一个混合多属性决策问题。本文利用混合多属性理论中的TOPSIS原理[12-13]，构建铁路站位方案评价和比选模型。

3.2 铁路站位方案评价模型

3.2.1 三角模糊数

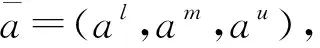
(7)

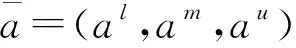
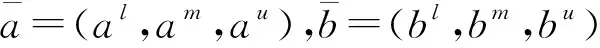
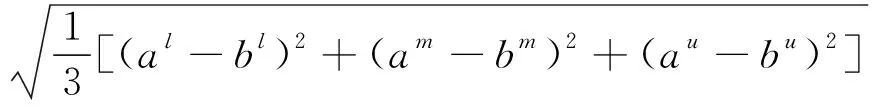
(8)

3.2.2 方案综合评价和比选步骤

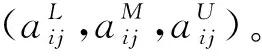
表2 语言类模糊数与三角模糊数的转化关系

传统的铁路方案评价方法主要采用专家打分，使用1、3、5、7等确定的数对定性指标进行量化[15]，这种处理方法对指标的模糊性等不确定性特征考虑不足。因此，本文利用三角模糊数对定性指标进行量化，这样就能充分考虑到定性指标量化后的模糊性，使得最后的综合评价结果更接近于实际情况。

将定量指标取值的实数和定性指标取值量化后的三角模糊数进行组合，构成站位方案综合评价和比选的决策矩阵A=(aij)mXn。

(2)分别利用式(9)、式(10)和式(11)、式(12)对定量指标取值的实数和定性指标取值的三角模糊数进行规范化处理，得到规范化矩阵S=(sij)mXn。

①对于定量指标取值为精确数时，对于效益型指标，规范化方法为

(9)

对于成本型指标，规范化方法为

(10)

②当定性指标取值为三角模糊数时，对于效益型指标，规范化方法为

(11)

对于成本型指标，规范化方法为

(12)

(3)利用式(6)计算指标的权重W。然后利用权重W对规范化矩阵S进行加权，得到加权规范化矩阵Y=(yij)mXn，其中yij=wj×sij，i=1，2，…，m，j=1，2，…，n。

(4)利用混合TOPSIS法原理，确定方案评价值并进行方案排序。

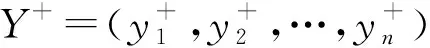
a.对于定量指标指标

(13)

b.对于定性指标

j=k+1,…,n;

(14)

j=k+1,…,n

(15)

②计算各备选方案到正理想方案与负理想方案的距离。

第i个方案到正理想解Y+的距离为

(16)

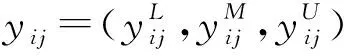
第i个方案到负理想解Y-的距离为

(17)

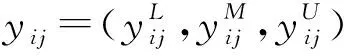
③计算各方案的综合相对贴近度

(18)

显然综合相对贴近度Pi的值介于0～1。当Pi=1时，站位方案综合评价值最高；当Pi=0时，站位方案综合评价值最低。

(5)根据Pi值的大小对方案进行排序：Pi值越大，则方案整体评价值越大，表明方案Xi越优；Pi值越小，则方案整体评价值越小，表明方案Xi越差。

4 实例分析

结合云桂铁路广南站位方案研究，进行方案评价和比选实例分析。云桂线位于广西和云南范围内，线路长714.559 km。广南县位于云南省东南部，文山州东北部，滇、贵、黔三省(区)交界处。广南县人口76万人，居云南省第6位，经济发展水平远低于全国、全省平均水平，是国家扶贫开发工作重点县和云南省重点扶持的人口大县；广南县境内自然资源丰富，有八宝贡米、生态油茶等生物资源，矿产、水能资源也非常丰富，有全国第二大锑矿企业木利锑业，可开发水能资源31.9万kW；境内自然环境优美，历史底蕴深厚，民族文化多姿多彩，“世外桃源”坝美景区、省级风景名胜区八宝和省级历时文化名城莲城在省内外的知名度日趋提升，旅游业发展潜力巨大。为了靠近主要经济据点，吸引当地客货流，可行性研究阶段对靠近广南县城的派播站位方案进行了深入研究，同时研究了昔板站位方案、派播站位方案、板构站位方案和上锅寨站位方案，见图1。

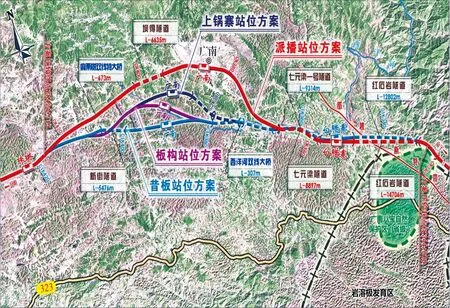
图1 广南站位方案比较示意

根据本工程评价需要，选取线路总长度、拆迁建筑物、吸引客货流的能力等定量和定性相结合的12个指标，分别用C1，C2，…，C12表示(其中C8，C11，C12为效益型指标，其余都为成本型指标)。通过对该段铁路可研报告的整理，得出上述4个方案各指标取值的基础数据，并聘请专家采用语言类模糊数对定性指标进行赋值，见表3。

4.1 方案评价和比选

(1)定性指标的语言类模糊数取值量化为三角模糊数，见表4。

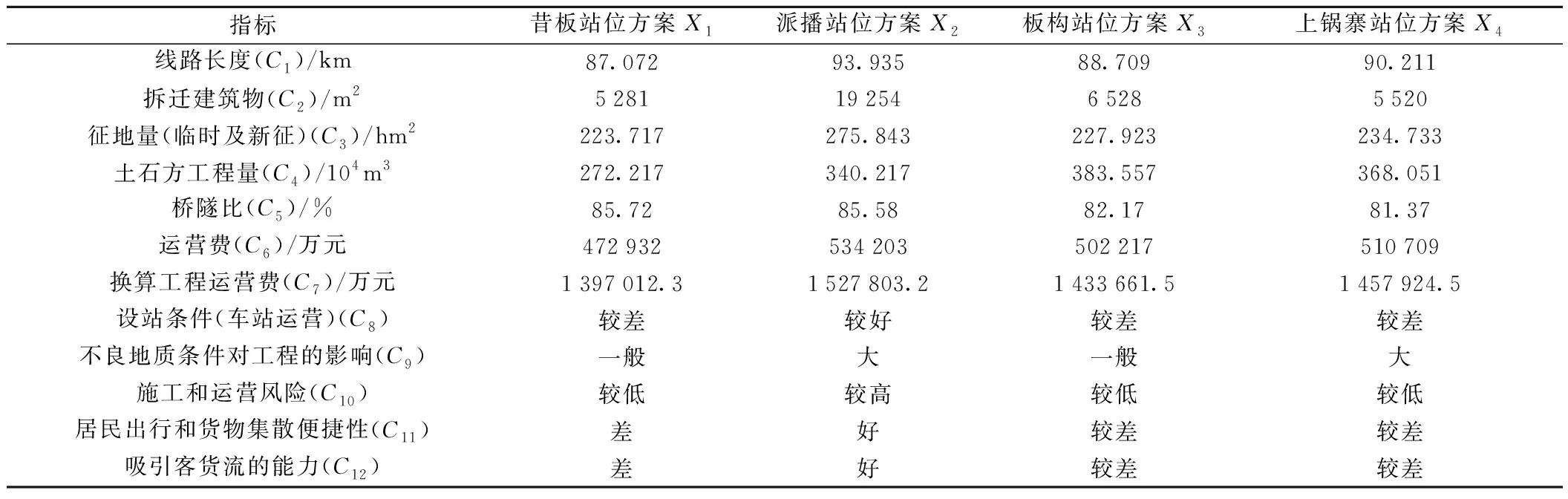
表3 各站位方案及对应指标的取值

表4 定性指标量化值

(2)将定性指标取值的三角模糊数与定量指标取值精确实数结合起来，构成线路方案评价的决策矩阵A=(aij)4×12。然后分别利用式(9)、式(10)和式(11)、式(12)对决策矩阵进行规范化处理，得到规范化矩阵

(3)利用式(6)确定指标权重，得到

W=(0.009 0，0.105 4，0.023 4，0.041 8，0.007 3，0.014 1，0.010 5，0.129 1，0.132 2，0.129 1，0.199 1，0.199 1)。

(4)用权重W对规范化矩阵S进行加权，得到加权规范化矩阵Y，并计算得到正负理想方案。然后，计算各备选方案到正理想方案与负理想方案的距离，并得到各方案的综合相对贴近度为

P1=0.270 3，P2=0.730 1，

P3=0.419 0，P4=0.288 5

因此，方案排序结果为X2>X3>X4>X1，派播站位方案比其他3个站位方案更优。

4.2 结果分析

对表3给出的4个站位方案的指标数据进行分析可知，派播站位方案线路最长、征地拆迁工程最多、桥隧比和换算工程运营费都很高，但该方案有利于吸引客货流、方便旅客出行和货物集散以及设站条件最好，由于这3个定性指标的权重相对更大，使得派播站位方案的综合评价值仍然达到了0.7以上，也是4个站位方案中经综合定性、定量比较后的最优方案。上述计算得出的结果与设计单位专家通过对定量指标的计算和对定性指标的分析后所做出的决策结论一致。

5 结论

根据铁路站位方案评价和比选的特点，建立了基于混合多属性决策的方案评价模型。模型弥补了层次分析法和模糊综合评价等传统评价方法的不足，根据指标原始数据的差异性大小确定指标权重，使得权重趋于更科学、合理；同时，利用混合多属性决策，实现了定量指标和定性指标的综合比选，使得决策结果更加均衡化。最后实例分析表明，本文模型可为铁路站位方案比选提供定量化的决策支持，具有较好的可靠性和实用价值。

[1] 周承汉.基于三角模糊数的高速铁路线站位方案比选[J].铁道科学与工程学报，2016，13(3)：435-440.

[2] 唐经勇.高速铁路客运站选址方法研究[D].成都：西南交通大学，2008.

[3] 张世升.基于铁路沿线大型站点的综合开发研究——以日本京都火车站综合体谈西安站改[J].铁道标准设计，2016，60(1)：114-118.

[4] 乔俊飞.郑州至新郑机场城际铁路机场段线路方案研究[J].铁道标准设计，2016，60(1)：52-55.

[5] 罗圆，姚令侃，朱颖.基于离差投影的山区铁路选线方案比选模型[J].铁道标准设计，2013，57(10)：1-6.

[6] 罗圆，姚令侃，朱颖.基于效用理论的铁路选线方案比选模型[J].西南交通大学学报，2013，48(6)：1008-1015.

[7] 罗圆.基于不确定性分析的铁路选线方案评价方法研究[D].成都：西南交通大学，2016.

[8] 闫创.西安至韩城城际铁路线路走向方案研究[J].铁道标准设计，2016，60(8)：40-44.

[9] 陈俊，邵海鹏.铁路选线设计方案物元优选模型[J].铁道标准设计，2011(3)：5-8.

[10] 周宏安，刘三阳.基于离差最大化模型的模糊多属性决策投影法[J].系统工程与电子技术，2007，29(5)：741-744.

[11] 杨静，邱菀华.基于离差的模糊多属性决策法及其应用[J].系统工程，2008，26(6)：107-110.

[12] 夏勇其，吴祈宗.一种混合型多属性决策问题的TOPSIS方法[J].系统工程学报，2004，19(6)：630-634.

[13] 许海霖，张晶.基于改进TOPSIS模型的地铁网络节点重要性评价方法[J].铁道标准设计，2016，60(7)：19-24

[14] 廖勇.基于三角模糊数的铁路客运站选址方案评价方法[J].中国铁道科学，2009，30(6)：119-125.

[15] 贺晓霞，鲍学英，王起才.基于组合方法计算权重的绿色铁路客站综合评估[J].铁道标准设计，2016，60(4)：103-107.