重载铁路部分斜拉桥结构参数分析

李桂林

(中铁第四勘察设计院集团有限公司,武汉 430063)

1 概述

各种桥型对于跨度均有不同的适用范围，预应力混凝土连续梁存在自重较大等特点，应用于铁路桥梁时其主跨跨度一般在128 m范围内。部分斜拉桥作为一种连续梁拉索加劲结构，可扩展其跨度，应用跨度范围为140～280 m。与连续梁相比，部分斜拉桥具有提供较大的跨越能力、有效控制后期变形等优点；与常规斜拉桥相比其主要有节省工程量、结构刚度大、施工周期短等优势，因此在高速铁路、城际铁路及公路工程中得到广泛应用。

重载铁路作为纯货运铁路形式，与客运专线、高速铁路、客货共线铁路相比，存在设计荷载大、轴重重、列车荷载频繁等特点[1-2]。蒙华重载铁路跨越汉江时，考虑到与下游5×120 m公路连续梁桥对孔及经济性等边界条件，根据多方案比选，采用主跨248 m部分斜拉桥方案[3]。由于活载所占比重极大，直接采用目前典型的部分斜拉桥形式及结构设计参数范围，结构难以承受。为解决部分斜拉桥应用于重载铁路桥梁受力问题，对该桥各参数进行比较分析，确定部分斜拉桥应用于该桥位时的合理结构参数，并首次成功将部分斜拉桥应用于重载铁路[4-6]。部分斜拉桥效果图见图1。

图1 部分斜拉桥效果图

2 约束体系分析

本桥主跨跨度达248 m，又为重载铁路，仅列车荷载单项引起主墩支反力达49 280 kN，如采用塔梁固结、墩梁分离体系[7-10]，需特殊设计大吨位支座。理论上来说，宜优先考虑塔墩梁固结体系，避免设置大吨位支座。

该桥小里程侧主墩墩高18.2 m，大里程侧主墩墩高18.7 m(均为梁底至地面线之间的距离)，约为跨度的1/13.3。当采用塔墩梁固结体系时，由于主墩高跨比较小，若采用较刚的桥墩形式，温度产生自应力较大，墩底及主梁均承受较大拉应力作用，结构难以承受。此时若采用双肢薄壁墩等较柔的结构形式，则主墩截面面积及惯性矩均偏小，最大压应力已超目前最大混凝土强度等级压应力限值，结构受力性能差，且存在防撞能力差、侵占通航净空等不利因素。

从主梁受力分析，在恒载及列车荷载作用下，双肢薄壁体系能有效改善支点截面负弯矩和跨中截面正弯矩作用。但采用塔墩梁固结体系与塔梁固结、墩梁分离体系比较，温度引起主梁支点截面弯矩增大54倍，跨中截面弯矩增大34倍。同时，在预应力钢束布置一致的情况下，塔梁固结、墩梁分离体系时预应力效应能更有效的发挥，总体应力水平塔梁固结、墩梁分离体系偏优。

从活载位移结果比较分析，采用塔梁固结、墩梁分离体系时刚度为1/1 042，塔墩梁固结体系时刚度为1/1 941，可以看出塔墩梁固结体系能有效提高结构整体刚度，从刚度这方面分析，塔墩梁固结体系具有较明显的优势，但由于本桥为重载铁路，对结构刚度及行车舒适性等要求较低，结构刚度为非控制性因素。

综合分析，受桥位处墩高限制，采用塔墩梁固结体系时结构难以实现，比选后采用塔梁固结、墩梁分离体系，并于主墩设置190 000 kN球形支座，为目前国内第二大吨位，支座采用高性能材料及分部密封方案，保证耐久性、稳定性和长久使用寿命。

3 主梁梁高影响分析

为研究主梁高度对主梁受力性能的影响程度，研究主梁支点梁高为13、13.5 m和14 m，跨中梁高为6 m和6.5 m时梁高组合，分析主梁内力及应力情况。表1列出不同梁高时各控制点最不利荷载组合应力。

表1 主梁控制点应力对比

注：应力值以压为正。

增加支点梁高及跨中梁高，跨中下缘应力储备增幅在0.3 MPa以下；对中支点截面，最佳方案为14 m-6 m组合，中支点上缘压应力增加0.77 MPa；对于边跨来说，13.5 m-6.5 m组合最优，但与13 m-6 m组合仅差别0.05 MPa。总体来看，无论是增加支点梁高，还是跨中梁高，对截面应力改善影响程度均较小，而13 m-6 m组合时，主梁应力已呈现较好的应力状态，表明该梁高取值合适。中支点梁高13 m，跨中梁高6 m情况下，边跨上缘最大压应力为15 MPa，中跨上缘最大压应力为17.4 MPa，且跨中下缘压应力储备仍有1.5 MPa富余。中支点梁高采用13 m时，尝试减少跨中梁高至5.5 m，跨中混凝土上缘压应力高达19.7 MPa，次边跨支点上、下缘最大压应力均达到19.1 MPa，此时最小应力仅为0.12 MPa。表明该梁高偏小，不宜再减小梁高。

通过对梁高比较可知：在一定范围内无论是增加跨中梁高还是支点梁高，主梁应力改善影响程度均较小，同时主墩吨位将会超190 000 kN。当降低梁高时，主梁上缘压应力高达19.7 MPa，梁高不宜再降低。因此中支点—跨中梁高采用13 m-6 m组合较为合适。

4 预应力钢束布置对结构内力影响分析

本桥主梁为5跨连续梁形式，采用先合龙边跨后合龙中跨方案，需进行三次体系转换，预应力布置复杂。由于斜拉索对边支点及边跨跨中影响甚微，因此需要研究该区域顶底板钢束布置及张拉顺序形式对结构内力影响，同时分析中跨底板短束和长束对结构内力影响，确定最合理的预应力钢束布置方式。典型钢束布置示意如图2所示。

看完这封信，我的头一个反应是，糟了，白丽筠一定是寻了短见。我发了疯一般冲出家门，本能地朝白丽筠的住所奔去。只见她家的门大敞着，有工人搬着笨重的大件家具进进出出。我努力镇静自己，装出一副路人的好奇，朝门里探头张望，门里已经完全是另一个世界，哪里还有白丽筠住过的痕迹。

图2 典型钢束布置示意

对图2中6种对边跨影响较大的预应力布置形式及相应工况进行分析(均为2束19-φj15.2 mm钢束效应)，对结构影响主要呈现以下特性。

(1)边跨顶板短束T3在悬臂张拉阶段及在边跨合龙后张拉这两种工况下，轴力接近，均为6 500 kN左右。悬臂张拉工况在辅助墩产生弯矩为16 862 kN·m，截面上缘产生0.7 MPa压应力，截面下缘产生0.2 MPa拉应力；边跨合龙后张拉时弯矩10 467 kN·m，截面上缘产生0.6 MPa压应力，截面下缘产生0.1 MPa压应力。辅助墩位置上下缘均为控制区域，在上缘应力改善需求明显的情况下，可增加悬臂张拉短索根数，若上下缘应力均较为控制，宜增加边跨合龙后短索根数。

(2)边跨顶板长索T10(未越过边跨合龙段)，该类型钢束主要为改善辅助墩顶受力。悬臂阶段张拉时，于辅助墩顶区域产生正应力，但边跨塔端无索区次内力作用明显。边跨合龙后张拉和中跨合龙后张拉弯矩图接近，于辅助墩顶区域为负效应。从3种张拉阶段产生的弯矩(图3)来看，以悬臂阶段张拉为优，但该类型钢束次内力负效应较明显，在满足施工阶段节段混凝土张拉钢束要求的前提下，应尽量减少该类型钢束布置。

图3 边跨顶板长索T10弯矩(单位：kN·m)

(3)边跨顶板长束T11(越过边跨合龙段)，在边跨合龙后及中跨合龙后张拉，弯矩图均接近，主要在边跨产生正弯矩，中跨产生负弯矩，且该钢束仅影响边跨及次边跨受力，对中跨弯矩影响甚微。

(4)边跨底板短束B1，于边跨合龙后张拉及中跨合龙后张拉各截面弯矩值接近，弯矩主要集中在钢束布置区域，且分布较均匀，近似呈矩形分布，约为14 800 kN·m，该类型钢束次内力效应较小。

(5)B5和B6弯矩图较为接近，主要在边跨产生负弯矩效应，呈近似梯形分布，于次边跨2/3范围内产生近似三角形分布正弯矩。B6钢束布置越过辅助墩，梯形分布负弯矩亦越过辅助墩，能改善辅助墩底应力水平。见图4。

图4 边跨底板长索B5弯矩(单位：kN·m)

5 桥塔刚度影响分析

桥塔采用双柱式，桥面以上塔高57.0 m，顺桥向塔底宽7.2 m，塔顶宽5.0 m；横桥向宽度2.8 m。为研究桥塔刚度对结构受力的影响，分析了以0.1、0.5、1、5、10倍桥塔刚度时结构特性。见表2。

表2 桥塔刚度对应工况控制截面弯矩对比

主力工况下，中支点截面最大弯矩随刚度增加而减少[11-15]，跨中截面弯矩随刚度增加先减少后增大，1倍桥塔刚度时最小。主力+附加力工况下，中支点截面弯矩随桥塔刚度增加而减小，10倍桥塔刚度时对应弯矩较之0.1倍桥塔刚度时弯矩减小12%，主跨跨中截面10倍桥塔刚度时对应弯矩较之0.1倍桥塔刚度时减小7%。

从表3可以看出，桥塔刚度增加10倍的情况下，结构整体刚度仅增加1.012%。

表3 桥塔刚度对应结构整体刚度值

从以上分析可知，重载铁路部分斜拉桥桥塔刚度对结构整体受力及结构刚度影响均较小，可在满足索鞍布置等构造及桥塔自身受力要求的前提下[16-18]，尽可能减少桥塔尺寸，降低桥塔混凝土用量。

6 桥塔高度影响分析

对35 m/40 m/45 m/50 m/57 m塔高时结构分析，控制截面弯矩如表4所示。

主力工况下，主梁中支点弯矩随桥塔高度增大而减小，57 m塔高时对应弯矩为35 m塔高时对应弯矩的63%，主梁跨中弯矩随桥塔高度增加而减小，且降幅明显，57 m塔高时对应弯矩仅为35 m塔高时对应弯矩的51.6%。主力加附加力工况下，亦呈现出与主力工况下相似结论，57 m塔高时对应中支点弯矩为37 m塔高时的64.7%，57 m塔高时跨中截面弯矩为35 m塔高时的58.1%，降幅均非常明显。

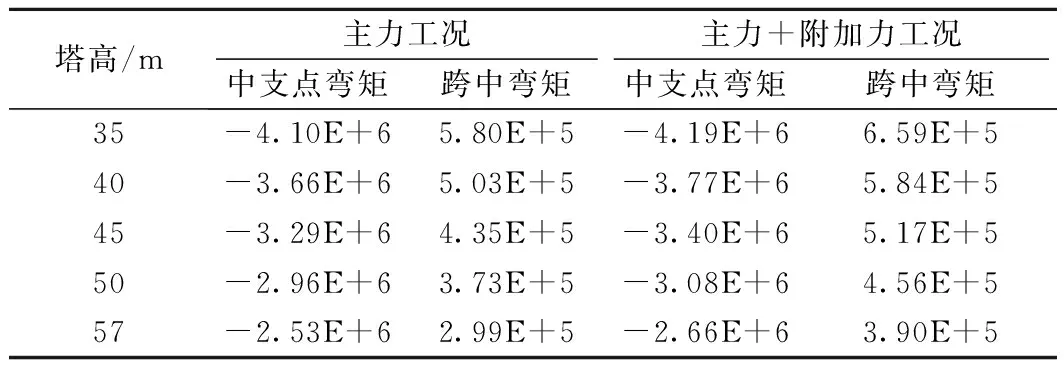
表4 主力工况下控制截面弯矩对比 kN·m

由表5可以看出，桥塔高度对主梁刚度有一定程度影响，当桥塔高度降低38.6%，主梁刚度降低17.1%。

表5 塔高对应结构刚度值

综上所述，塔高是该重载铁路部分斜拉桥的一个重要参数，其对主梁主跨支点截面及跨中弯矩均有很大影响，并在一定程度上影响着主梁刚度。

7 索塔梁刚度匹配分析

对于预应力混凝土连续梁，在跨度确定的情况下，梁高为桥梁结构刚度的控制因素。对于预应力混凝土部分斜拉桥，除梁高外，桥塔和斜拉索均对结构刚度存在较大影响。根据梁高对比分析，本桥主梁在截面应力优化且强度满足规范要求的条件下，采用支点-跨中梁高13 m-6 m组合，不考虑设置桥塔及斜拉索时，主梁在静活载作用下最大位移为355 mm，主梁刚度为1/698。考虑桥塔及斜拉索之后，结构刚度为1/1042，可知该桥主梁对整体刚度的贡献值为67%，桥塔及斜拉索对整体刚度贡献值为33%。桥塔和斜拉索为相关构件，桥塔自身刚度变化对主梁刚度影响很小，而当桥塔高度降低38.6%，主梁刚度降低17.1%，刚度为1/864，在此基础上，斜拉索截面刚度降低38.6%，则主梁刚度变为1/827，结构刚度仅下降4.3%。从改变桥塔自身刚度、桥塔高度和斜拉索截面刚度相同比例的结果来看，改变桥塔高度对结构刚度的影响程度更大。

8 结论

本结构为混凝土主梁采用斜拉索加劲的部分斜拉桥形式，在重载铁路工程项目中属首次采用，填补了重载铁路桥型空白。本桥通车运营时间约为2018年12月。通过对该桥的各设计参数的比较分析，主要得到以下结论。

(1)对比分析塔墩梁固结体系和塔梁固结、墩梁分离体系，从结构受力合理性等方面考虑，本桥采用墩梁分离体系要优于双肢薄壁墩体系。

(2)以中支点-跨中梁高采用13 m-6 m作为基本组合梁高，在一定范围内无论是增加跨中梁高还是支点梁高，主梁应力改善影响程度均较小，跨中梁高减少至5.5 m时，主梁上缘压应力高达19.7 MPa，此时上缘最小压应力仅为0.12 MPa，梁高不宜再降低。中支点-跨中梁高采用13 m-6 m组合是合理选择。

(3)短预应力钢束引起弯矩主要分布于预应力钢束布置区域，且近似呈矩形分布，预应力次内力效应较小；边跨顶板长束效应较差，应适当减少该类型钢束布置，边跨底板长束弯矩在边跨区域负弯矩呈近似梯形分布，于次边跨正弯矩呈近似三角形分布，次内力效应明显。

(4)重载铁路部分斜拉桥桥塔刚度对结构整体受力及结构刚度影响均较小，可在满足索鞍布置等构造及桥塔自身受力要求的前提下，尽可能减少桥塔尺寸，降低桥塔混凝土用量。

(5)结合重载铁路特点，通过对桥塔高跨比研究，确定桥塔高采用57 m，高跨比为1/4.35，普通铁路部分斜拉桥桥塔高跨比一般在1/7.0～1/7.5，较普通铁路部分斜拉桥高跨比大。高跨比增大，能有效改善重载铁路部分斜拉桥主梁受力，保证在重载铁路荷载作用下，结构具有足够的强度、刚度等性能。

(6)该重载铁路部分斜拉桥结构刚度主要由主梁提供，约占67%，主塔及拉索对整体刚度贡献值为33%，主塔自身刚度对结构整体刚度影响甚微，桥塔高度对结构刚度影响较明显。

[1] 金福海，文望青，许三平.蒙西至华中地区铁路煤运通道设计活载选用初探[J].铁道标准设计，2013，57(3)：48-52.

[2] 李桂林.超大跨度铁路桥梁列车加载长度研究[J].铁道标准设计，2015，59(3):64-68.

[3] 严定国.蒙西至华中地区铁路煤运通道汉江特大桥方案设计[J].铁道标准设计，2016，60(7)：99-103.

[4] 国家铁路局.TB/T 3466—2016 铁路列车荷载图示[S].北京：中国铁道出版社，2016.

[5] 国家铁路局.TB 10625—2017/J2289—2017 重载铁路设计规范[S].北京：中国铁道出版社，2017.

[6] 国家铁路局.TB 10092—2017/J462—2017 铁路桥涵混凝土结构设计规范[S].北京：中国铁道出版社，2017.

[7] 张雷.京沪高速铁路津沪联络线矮塔斜拉桥设计[J].桥梁建设，2012，42(4)：69-74.

[8] 王富君.跨既有铁路矮塔斜拉桥设计与转体施工[J].铁道标准设计，2011(3)：58-61.

[9] 刘士林.斜拉桥设计[M].北京：人民交通出版社，2006.

[10] 严国敏.现代斜拉桥[M].成都：西南交通大学出版社，1999.

[11] 蔺鹏臻.部分斜拉桥的力学性能及其界定[J].铁道学报，2007，29(2)：136-140.

[12] 燕明.部分斜拉桥的概念与结构设计[J].交通科技与经济，2006(3)：11-13.

[13] 康炜.小西湖黄河大桥部分斜拉桥结构分析[J].铁道标准设计，2004(11)：88-90.

[14] 郑一峰，黄侨，张连振.部分斜拉桥结构对比分析[J].公路，2005(11)：15-21.

[15] 张海，吴大宏.津保铁路矮塔斜拉桥设计关键技术研究[J].铁道标准设计，2013，57(11)：55-58.

[16] 陈虎成，石雪飞.部分斜拉桥结构性能研究[J].结构工程师，2004(3)：27-31.

[17] 陈从春，周海智，肖汝诚.矮塔斜拉桥研究的新进展[J].世界桥梁，2006(1)：70-73.

[18] 陈军刚，陈孔令，张焱.南盘江特大桥部分斜拉桥设计[J].桥梁建设，2009(5)：36-39.