新型支承体系多跨矮塔斜拉桥合龙方案研究
罗如登,刘铸,陈立军,王高辉,李先海
(1.中南大学 土木工程学院,湖南 长沙 410075;2.中国建筑第五工程局,湖南 长沙 410004)
矮塔斜拉桥是介于梁式桥和斜拉桥之间的新颖桥型,以主梁的受弯、受压与拉索的受拉来共同承受竖向荷载[1-2]。多跨矮塔斜拉桥合龙段数目多,合龙方案的不同将引起桥梁较大的次内力及内力重分布,继而影响成桥的受力状态等[3-5]。莫恺筠等[6]对某三跨矮塔斜拉桥不同合龙方案进行研究,得出先中跨合龙情况下全部合龙完成后再进行体系转换方案更优。黄俊杰[7]对五跨矮塔斜拉桥各构件进行静力特性研究,最优方案为先边跨合龙再次边跨合龙最后中跨合龙。何祖发等[8]通过对七塔矮塔斜拉桥结构性能进行研究,对合龙顺序及工艺进行了优化。焦亚萌等[9]通过对十跨单索面矮塔斜拉桥合龙顺序进行研究,得到采用先静定中跨小合龙,再大合龙方案最优。目前在建的汕头市新津河特大桥为五塔六跨矮塔斜拉桥,采用一种新型单墩双排8支座可调高可测力支承体系。双排支承体系极易出现受力不均衡现象,并且在收缩徐变影响下会出现支承反力重分配,导致桥梁支座出现部分支座脱空,而另外部分支座压缩变形过大而使得支座寿命缩短,甚至破坏[10]。本文通过对该桥多种合龙方案下全桥应力状态、线形、支承体系受力均衡性和成桥索力等进行对比分析,得出该桥最佳合龙方案。
1 工程概况
新津河五塔六跨单索面矮塔斜拉桥,桥跨布置为(68+4×120+68)m,采用塔梁固结、墩梁分离体系,主梁采用宽幅单箱三室结构,上部结构混凝土强度均为C60。为满足城市桥梁景观要求,主塔设计为倒U型,主墩设置为U型,两者呼应形成“水滴”造型。墩顶纵向设置一种新型双排支承体系,每排横向设置4个支座。为防止双排8支座支承体系不均衡受力,采用可调高可测力支座,成桥后须根据支座受力状态对全桥支座进行调控。图1所示为主桥及支座布置图,从左至右墩号依次为29号~35号。
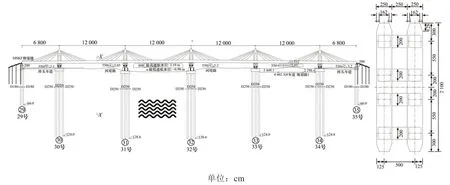
图1 主桥及支座布置图Fig.1 Layout of main bridge and support
新津河特大桥主桥设计合龙方案为先边跨合龙(29号~30号,34号~35号),再次边跨合龙(30号~31号,33号~34号),最后中跨合龙(31号~32号,32号~33号)。中跨墩(31号,32号)为水中墩,由于地质条件优于陆地墩,实际施工进度较快,中跨梁段将率先施工并合龙,原主桥设计合龙方案需调整变更。本文将对比研究合龙方案变更对全桥力学性能的影响,并确定该桥最佳合龙方案。
2 合龙方案
新津河特大桥主桥采用挂篮悬臂对称浇筑施工,由于孔跨较多,原设计和变更的合龙方案包括2种合龙顺序及4种合龙工艺。
2种合龙顺序如下:
1)边跨合龙→次边跨合龙→中跨合龙,简称为合龙顺序B;
2)中跨合龙→次边跨合龙→边跨合龙,简称为合龙顺序Z。
4种合龙工艺如下:
1)合龙钢束一次性张拉→体系转换→下一个合龙段施工,简称为工艺 1;
2)体系转换→合龙钢束一次性张拉→下一个合龙段施工,简称为工艺 2;
3)先张拉部分合龙钢束→体系转换→张拉剩余合龙钢束→下一个合龙段施工,简称为工艺 3;
4)先张拉部分合龙钢束→体系转换→下一个合龙段施工→全桥合龙→张拉全桥剩余合龙钢束,简称为工艺4。
3 新津河特大桥有限元模型
采用Midas Civil有限元软件,建立全桥有限元模型。主梁、主塔、主墩、承台及桩基均采用梁单元进行模拟,斜拉索采用桁架单元进行模拟,桩土效应通过土弹簧进行模拟,全桥共划分为10 262个梁单元和100个桁架单元。图2所示为全桥及支座有限元模型图。

图2 全桥及支座有限元模型Fig.2 Finite element model of the whole bridge and support
4 各合龙方案下力学性能研究
4.1 主梁应力
对不同合龙方案下施工过程及成桥后的主梁最大应力进行对比分析,结果见表1。表中应力以拉应力为正,压应力为负;括号外为合龙顺序B应力值,括号内为合龙顺序Z应力值;后文同表示。
表1中各状态下,各合龙方案下计算结果均满足规范对施工应力、短期效应和长期效应不大于允许应力的要求[11]。
从表1中的数据可以看出,合龙顺序的改变对施工过程中主梁应力有一定的影响,但合龙顺序的改变并不改变二恒铺装及收缩徐变10 a状态下主梁的受力状态。相同合龙顺序下,不同合龙工艺各施工阶段主梁应力状态基本一致,改变合龙工艺对主梁的应力影响较小。
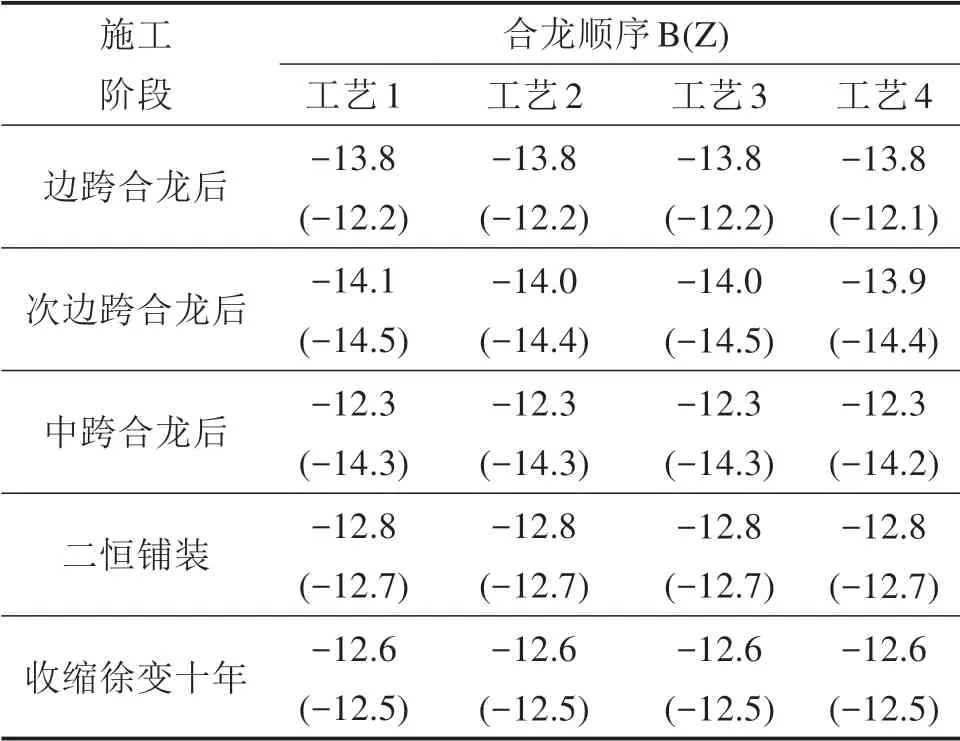
表1 主梁应力对比Table 1 Comparison of main beam stress MPa
4.2 主梁挠度及合龙段高差
对二恒铺装和收缩徐变10 a状态下不同合龙方案主梁挠度进行对比分析,结果如图3和图4所示。B(Z)-X表示为二恒铺装状态,B(Z)-X′表示为收缩徐变10 a状态,B(Z)表示合龙顺序,X表示合龙工艺,挠度值以竖向向上为正。
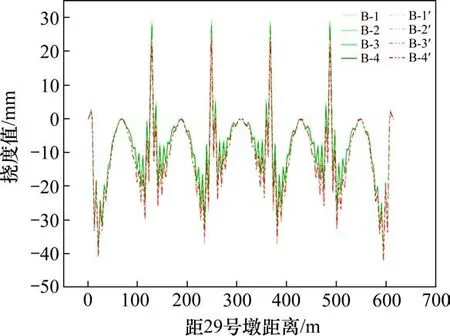
图3 合龙顺序B主梁挠度Fig.3 Girder deflection diagram of closure sequence B
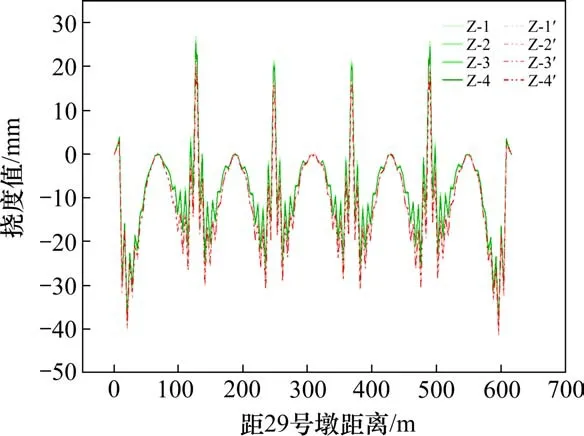
图4 合龙顺序Z主梁挠度Fig.4 Girder deflection diagram of closure sequence Z
由图3和图4可知,同状态下,不同合龙工艺的挠度曲线整体趋势一致,合龙工艺的不同对线形的影响很小。收缩徐变10 a状态下,次边跨和中跨挠度低于二恒铺装状态下的挠度,对结构不利。因此,在施工阶段设置预拱度时应考虑桥梁收缩徐变,使得线形更加理想[12-14]。
由以上分析,合龙工艺对挠度影响很小,且主梁挠度趋势在二恒铺装及收缩徐变状态下整体趋势一致,故选取二恒铺装状态下的其中一种工艺(工艺1)对合龙顺序进行挠度对比分析,结果如图5所示。主梁合龙段两侧挠度如表2所示,左侧表示合龙段靠近29号墩侧。
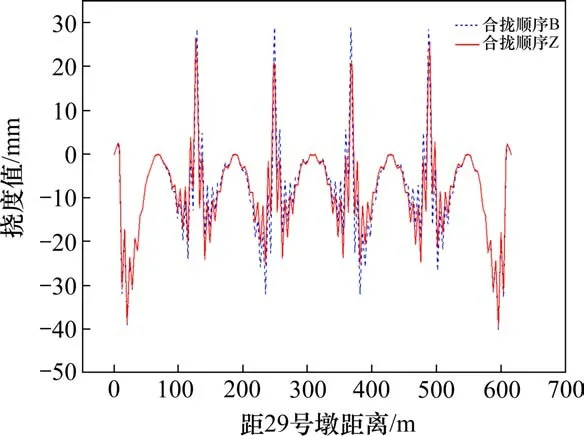
图5 二恒铺装主梁挠度Fig.5 Girder deflection of phase II dead load pavement
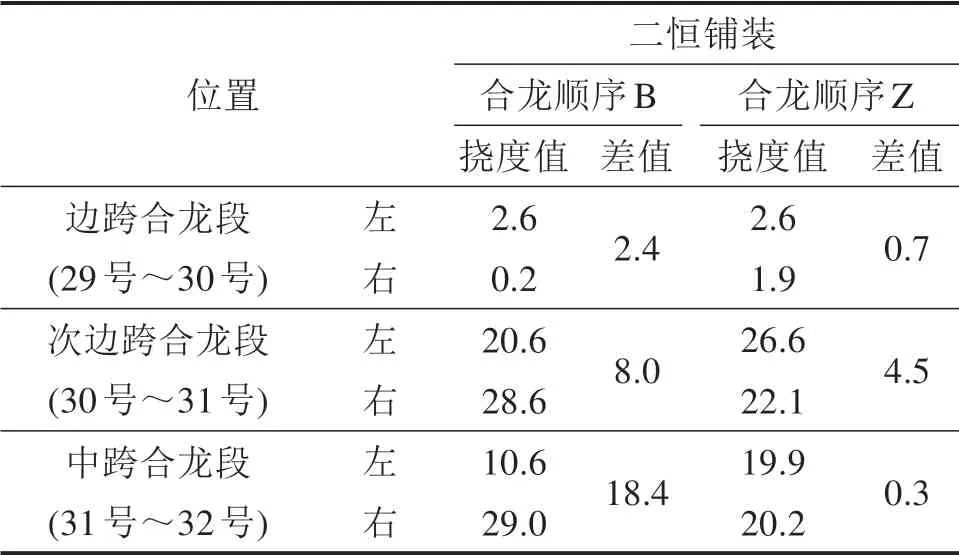
表2 合龙段两侧挠度Table 2 Deflection on both sides of closure section mm
由图5以及表2可知,不同合龙顺序下主梁边跨挠度基本一致,然而对于次边跨和中跨影响较大。在合龙顺序B下,最大突变值为18.4 mm,位于中跨;在合龙顺序Z下,最大突变值为4.5 mm,位于次边跨。合龙顺序Z下合龙段高差较小,更有利于合龙段施工。新型支承体系矮塔斜拉桥其主梁刚度大,同时双排支承体系在墩顶顺桥向间隔一定距离设置支座,实现了双排支座之间主梁的竖向约束和转动约束,表现为具有临时固结的“刚域”效应[15]。新型支承体系矮塔斜拉桥采用合龙顺序Z进行施工具有合理性,且合龙顺序Z下主梁线形表现得更优。
4.3 塔底应力
对不同合龙方案下的塔底应力进行研究,研究结果如表3所示。
从表3可知,各计算方案下塔底应力结果均满足规范要求[11]。合龙顺序及合龙工艺对塔底应力的影响较小,不同合龙方案最大差值为0.3 MPa。
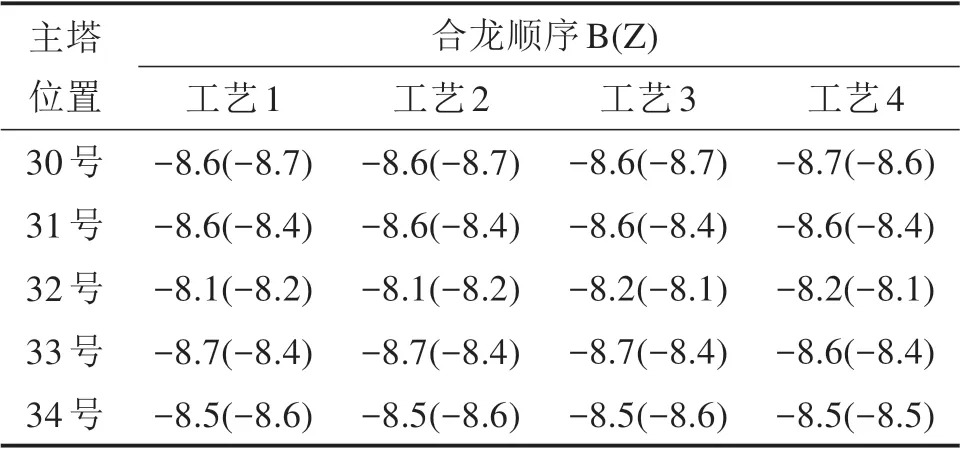
表3 塔底应力对比Table 3 Tower bottom stress comparison MPa
4.4 塔顶位移
对不同合龙方案下的塔顶顺桥向位移进行研究,研究结果如表4所示。表中位移以向35号塔变形为正,向29号塔变形为负。
从表4可知,各合龙方案下塔顶位移均较小。与传统单排支承体系相比,双排支承体系下塔顶顺桥向位移约为单排支承体系下的1/10[7-8]。新型双排支承体系下,主墩墩顶支座数量增倍,主梁的竖向荷载可更多的通过支座向下传递给墩柱,大幅度分担了通过斜拉索传递给主塔的荷载,从而有效控制了塔顶位移量。
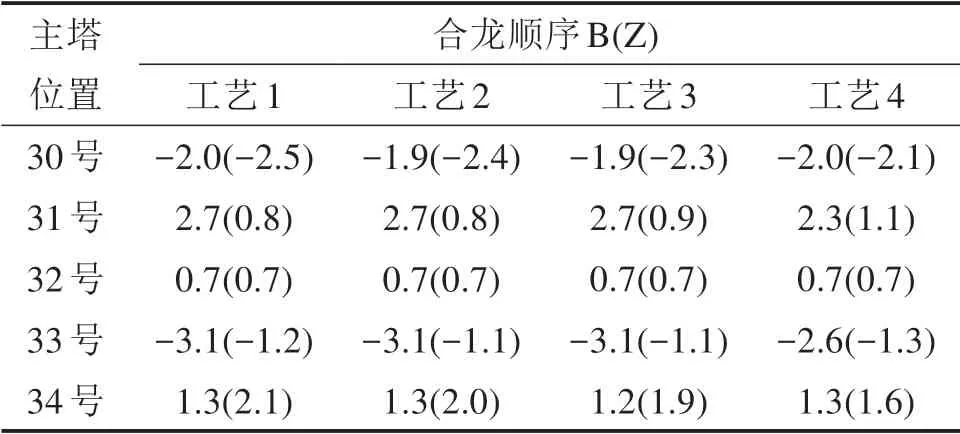
表4 塔顶顺桥向位移Table 4 Tower top longitudinal displacement mm
合龙顺序对塔顶位移的影响主要表现在次边塔(31号,33号),合龙顺序B下塔顶顺桥向位移为合龙顺序Z下的2~3倍,对中塔及边塔塔顶位移影响较小,合龙顺序Z较合龙顺序B更优。合龙工艺对塔顶顺桥向位移值影响较小,最大差值为0.5 mm,合龙工艺4较优于其他3种合龙工艺。
4.5 支承体系受力均衡性
对同墩双排8支座支承体系受力均衡性进行对比分析,结果见表5和表6。表中正值表示支座支反力靠近中跨侧大于边跨侧。
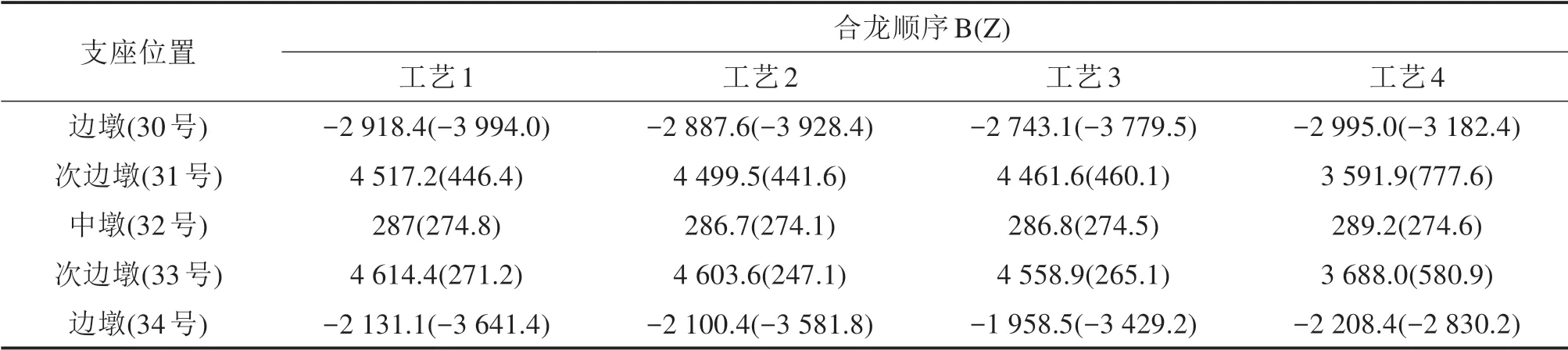
表5 二恒铺装双排支反力偏差对比Table 5 Comparison table of reaction force deviation of double row support in Phase II dead load pavements kN
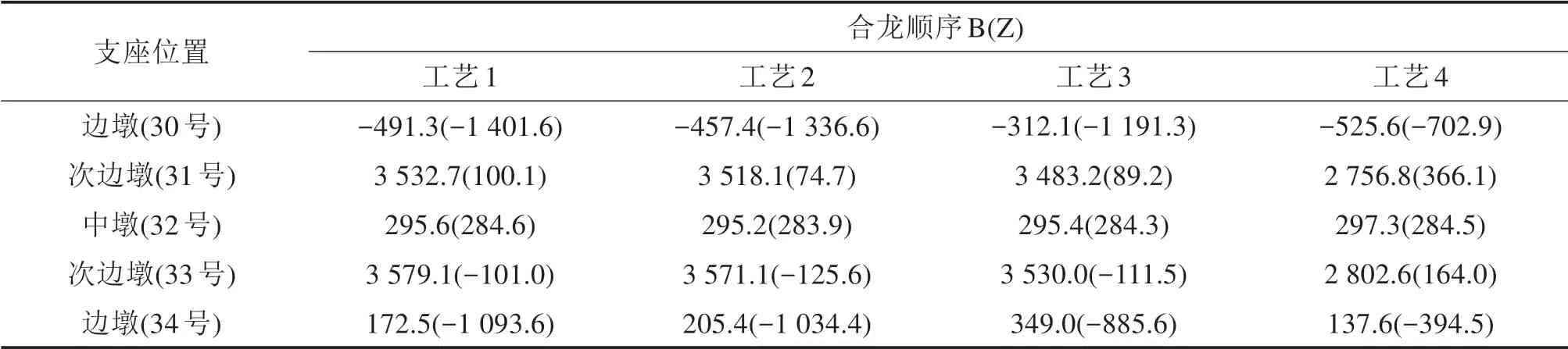
表6 收缩徐变十年双排支反力偏差对比Table 6 Comparison table of ten year support reaction deviation of double row support in shrinkage and creep kN
由表5和表6可知:二恒铺装和收缩徐变2种状态下各合龙方案双排支承体系均存在受力不均衡现象。为研究合龙方案对支承体系受力均衡性的影响,本文主要从双排支座支反力偏差量和成桥后支座调整难易程度2个方面进行分析。
合龙顺序B在二恒铺装状态下双排支反力偏差主要表现在边墩及次边墩,分别为2 995.0 kN和4 614.4 kN,在收缩徐变10 a状态下双排支反力偏差主要表现在次边墩,为3 579.1 kN;合龙顺序Z在二恒铺装状态和收缩徐变10 a状态下双排支反力偏差均表现在边墩,分别为3 994.0 kN和1 401.6 kN。收缩徐变作用会使支反力发生一定的重分配,使得支承体系受力更均衡。合龙顺序B在2种状态下双排支反力偏差显著位置发生变化,增大了后期支座调控难度;合龙顺序Z在2种状态下支反力偏差显著位置均发生在边墩,且均衡性优于合龙顺序B,可减少对支座的调控并且可在一定程度保证支承体系的受力均衡性。
合龙工艺对支反力的影响主要表现在边墩和次边墩位置,工艺4在二恒铺装下最大支反力偏差分别为3 182.4 kN和3 688.0 kN,在收缩徐变10 a下最大支反力偏差为702.9 kN和2 802.6 kN,支承体系受力均衡性均相对于其余3种工艺更优。通过合龙工艺优化可改善支承体系受力均衡性。
4.6 成桥索力
新津河矮塔斜拉桥斜拉索采用单索面体系,全桥具有一定对称性,根据拉索设计初拉力进行施工正装分析得到成桥索力,取全桥一半结构单侧拉索进行成桥索力对比分析。定义索力偏差系数P,如式(1)所示,分析合龙方案变更对成桥索力的影响,各合龙方案下索力偏差系数曲线如图6所示。其中位置编号中,前者表示墩号,后者表示索号,“1”索表示为靠近主塔侧,“5”索为外侧;图例编号中前者表示合龙顺序,后者表示合龙工艺。

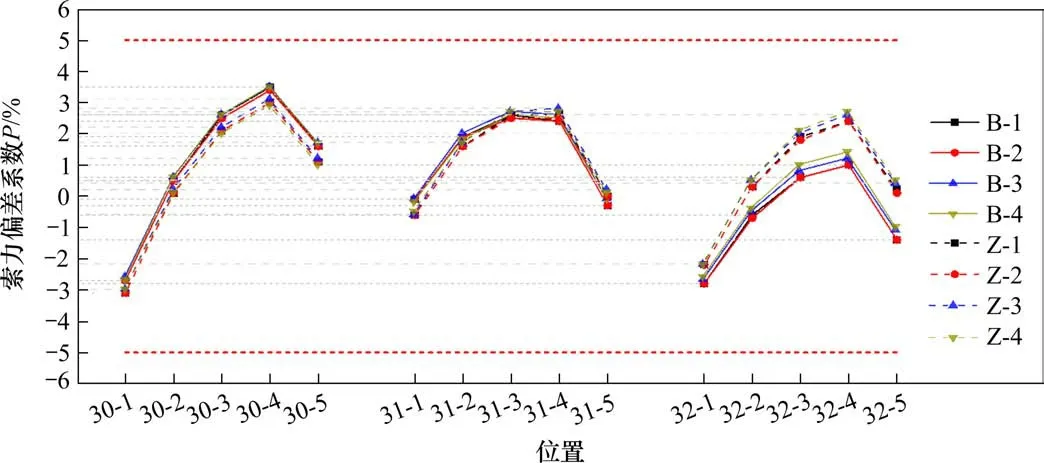
图6 索力偏差曲线Fig.6 Cable force deviation curves
由图6可知,斜拉索索力偏差主要表现在1号索和4号索,最大索力偏差为3.5%,各合龙方案均满足规范对索力允许误差的要求[16]。不同合龙工艺下成桥索力偏差曲线基本一致;合龙顺序对成桥索力的影响主要表现在中塔边索位置,两者最大索力偏差Pmax为1.5%。合龙工艺及合龙顺序对成桥索力的影响较小。
4.7 数值分析结果与实测数据对比
结合新津河特大桥现场施工状况及合龙方案研究,最终确定新津河特大桥采用合龙顺序Z与合龙工艺4的合龙方案进行合龙施工。通过在墩顶主梁腹板位置及塔底预埋振弦式应变计对主梁最大应力处及塔底应力进行监测,通过在主梁底板预埋短钢筋及在塔顶预设反光片分别对主梁线形及塔顶位移进行监测,支承体系采用可调高可测力支座,现场照片如图7所示。

图7 施工过程现场测点照片Fig.7 Photos of measuring points on site
对目前已完成施工阶段(中跨合龙完成)的数值分析结果与现场实测数据进行对比,取31号~32号结果进行对比分析,对比结果如表7所示,其中左侧表示合龙段靠近29号墩侧。两者结果整体趋势一致,吻合情况较好,验证了数值分析的可靠性及合龙方案的可行性。
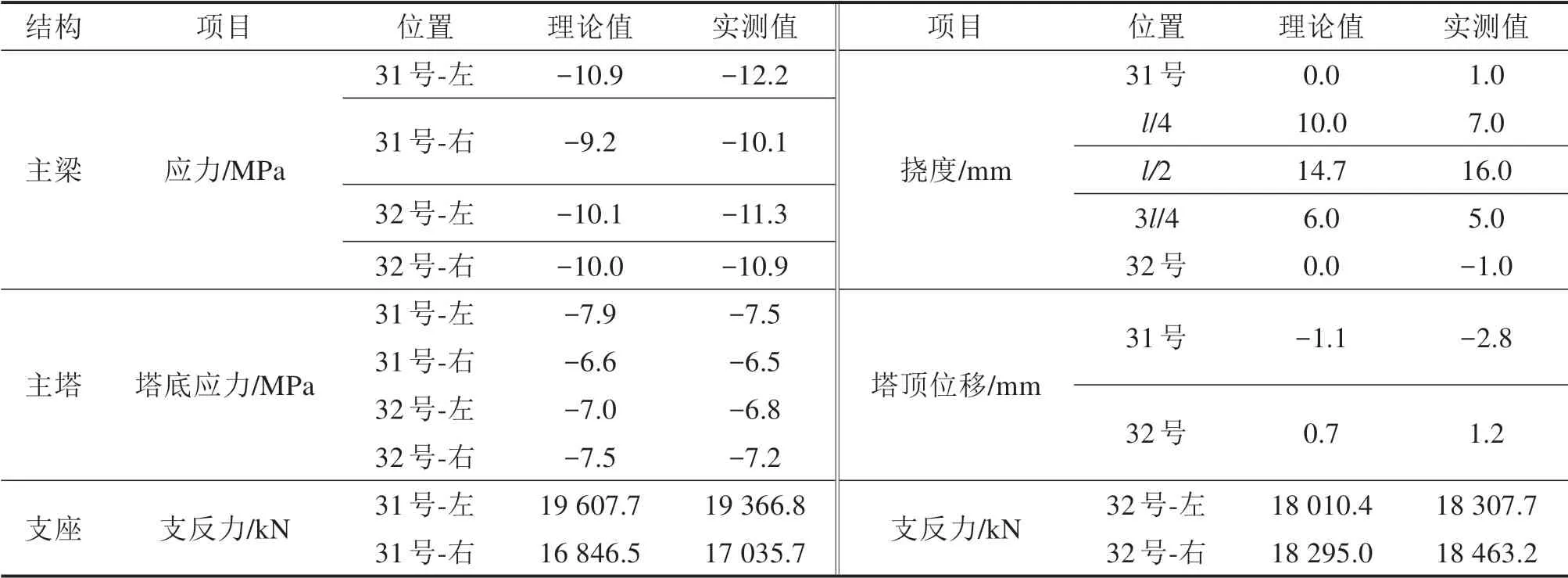
表7 数值分析与实测数据结果对比Table 7 Comparison table of numerical analysis results and measured data
5 结论
1)合龙顺序对结构线形影响较大,主要表现在主梁次边跨及中跨线形和合龙高差、次边塔顶位移。合龙顺序Z(先合龙中跨)的结构力学性能表现得更优。
2)支承体系受力均衡性受合龙方案的影响较大,主要表现在边墩和次边墩。优化合龙方案可改善支承体系受力均衡性,降低支座调控难度。合龙顺序Z和合龙工艺4(先张拉部分合龙钢束→体系转换→下一个合龙段施工→全桥合龙→张拉全桥剩余合龙钢束)支承体系受力均衡性最优。
3)合龙顺序Z和合龙工艺4为最优合龙方案,该方案实测数据与计算结果吻合较好,研究成果可为同类型桥梁提供参考。

