大型高铁车站最高聚集人数计算模型研究

米荣伟，帅斌，许旻昊，雷渝

(1.西南交通大学 交通运输与物流学院，四川 成都 611756；2.西南交通大学 综合交通运输智能化国家地方联合工程实验室，四川 成都 611756；3.西南交通大学 综合交通大数据应用技术国家工程实验室，四川 成都 611756）

中国国铁集团最新规划提出，截至2035年，我国高速铁路网将达到7万公里左右。在高速铁路建设过程中，高铁客运站最高聚集人数作为大型客运站规模设计的主要技术指标，对车站功能设置、客流组织、设施配置等起着至关重要的作用。针对现有最高聚集人数计算方法的不足，我国学者进行了深入研究。何宇强等[1-3]以旅客出行习惯和列车晚点为基础，引入了概率法、最坏情景法、模拟法，为最高聚集人数的计算提供了新的思路。刘启钢等[4-6]研究了列车发车时刻与最高聚集人数出现时刻的周期特性和作用规律。HOOGENDOORN等[7-8]基于NOMAD行人流量模型，从车站服务水平、旅客平均步行时间、车站拥挤程度等方面对车站设计进行了评估。赵文瑞等[9-11]分析了列车停站方案、列车运行里程、车站客流组织等因素对候车室候车能力的影响。BRUNETTA等[13-16]考虑了乘客性别、进站组织方式等因素，对旅客到站时间及候车时间进行了研究。根据上述研究成果可知，列车发车频率、旅客自身属性、车站公共交通配套设施等因素对旅客候车时间有着显著影响。虽然现有模型考虑了影响旅客候车时间的相关因素，但是不能准确模拟旅客聚集过程，且旅客最高聚集人数计算结果精度不高，主要存在以下不足：部分研究将列车简单划分为始发列车和途径列车，没有考虑到列车等级、列车发车时刻等因素对旅客候车时间的影响；同时部分研究忽略了车站所在城市常住人口、城镇人均可支配收入等因素对列车乘车人数的影响。本文参照《铁路旅客车站建筑设计(GB50226—2007)》规范，将最高聚集人数按照特定的“瞬时(8～10 min)”计算，以每5 min为一个“瞬时”单位记录车站旅客聚集人数。以广州局集团所有车站的38个典型时间段的数据为基础，分析高铁车站及列车属性对旅客聚集规律和列车乘车人数的影响，并用图解法的思想对现有计算模型进行优化，最后将成都东站作为案例进行分析，验证车站及列车属性的最高聚集人数计算模型的准确性。

1 现有最高聚集人数影响因素

现有文献指出影响旅客最高聚集人数的因素主要有列车开行方案、旅客聚集规律、列车乘车人数等[6]。由于列车开行方案主要由车站列车运行图决定，因此本文主要研究旅客聚集规律和列车乘车人数对最高聚集人数的影响。

1.1 旅客聚集规律

1.1.1 旅客候车时间规律

收集广州局集团1 500万余次旅客取票数据作为原始数据库。为了保证样本数据的有效性，按照下列原则对数据进行筛选：1)删除重复进站的旅客进站数据及空行；2)删除列车发车后进站旅客进站数据；3)删除列车发车时间前5 h之外的旅客进站数据。以广州局集团所有车站有效取票数据为基础，通过记录旅客进站时间及旅客乘坐列车车次，推算出候车旅客在站内停留时间及开车前每分钟到达人数占总乘车人数的比例，得到旅客在候车厅内的候车规律。采用对数正态分布、威布尔分布、复合负指数分布、有理函数分布对数据进行拟合，求得拟合函数参数并绘制出拟合函数曲线。

分析结果表明：所有乘客平均候车时间为44.42 min，约28.89%的旅客候车时间小于30 min，约51.33%的旅客候车时间为30～60 min之间，约19.78%的旅客候车时间大于60 min。广州南站旅客平均候车时间为58.15 min，在节假日期间旅客平均候车时间为59.17 min，非节假日期间旅客平均候车时间为56.65 min。

以G6301列车旅客候车规律为例，拟合函数及拟合结果如表1所示。结合图1拟合效果可知，对数正态分布拟合单峰的聚集趋势较好，威布尔分布和复合负指数分布适用于单峰聚集趋势，但是效果相比对数正态分布较差，有理函数可以较好拟合单峰及多峰趋势的旅客候车规律。因此本文选取对数正态分布和有理函数分布研究旅客候车规律与车站及列车属性的相关性。

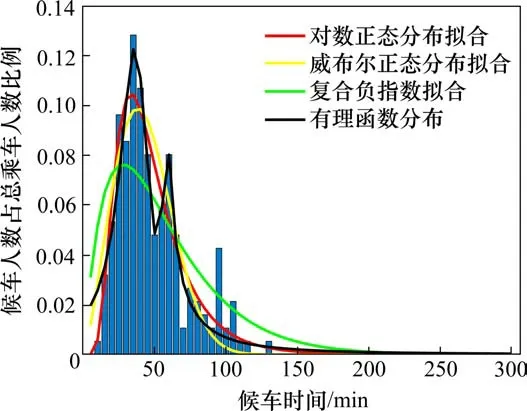
图1 广州南站G6301列车旅客候车规律Fig.1 Gathering rules of passengers on G6301 train at Guangzhou south railway station

表1 G6301列车旅客候车时间分布拟合Table 1 Distribution fitting of passenger waiting time for G6301 train

通过绘制各相关属性与对数正态分布、有理函数分布参数的箱型图(如图2)，分析发车时刻、车站属地类型、是否始发、列车类型、乘车人数、轨道交通衔接、常住人口、可支配收入与拟合函数参数之间的相关性，可以发现有理函数分布参数取值较为分散且与各属性间相关性较低，计算新建高速铁路车站旅客聚集过程时参数取值较难确定；对数正态分布参数与各属性间呈现较强相关性，且能较好拟合出旅客聚集趋势。因此本文通过分析车站及列车各属性与对数正态分布参数之间关系研究旅客候车规律。

图2 列车乘车人数对参数影响(部分)Fig.2 Influence of the number of passengers on the parameters(partial)

为了进一步研究车站及列车属性与旅客候车规律之间的相关性，运用Kruskal-Wallis检验算法对上述8类属性与对数正态分布参数进行相关性分析，其中μ的检验结果如表2所示。

表2 各属性与到达规律Kruskal-Wallis检验结果Table 2 Kruskal-Wallis test results of attributes and arrival rules

根据Kruskal-Wallis检验结果发现，列车乘车人数、列车类型、车站属地类型、列车发车时刻对旅客候车规律影响较大。由于基础数据量较大，为了确保数据处理的高效性、准确性，本文采用K-means聚类算法对旅客候车规律进行分析，其核心算法如式(1)所示。但是K-means需要设定k个初始聚类中心，为了判断数据聚类效果，引入Silhouette测度指标如公式(2)所示，分析聚类结果类内数据是否紧密，类间数据是否分离。

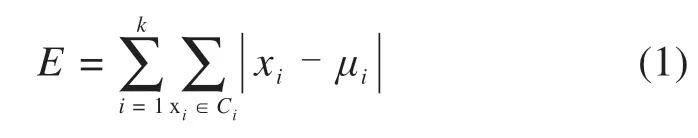
式中：E为数据集中所有对象误差的平方和；xi为第i类中的每个数据对象；μi为第i类的平均值；

式中：Sil为样本Aa的Silhouette测度值；ba为样本Aa到其他类内样本平均距离的最小值；aa为样本Aa到其所属类内其他样本的平均距离。

利用K-means算法计算各簇中乘车人数、列车类型、车站属地类型、列车发车时刻与对数正态分布参数取值，计算K值在1～300取值下Silhouette值如图3所示，根据曲线变化趋势可以发现，数据在50类内Sil指数呈现下降趋势；在50～150类内Sil指数波动性较大且呈递增趋势；在150类到300类内Sil指数呈现较慢的增长趋势，其中200类附近Sil指数取值较大且Sil值浮动范围较小。故以200类聚类分析结果为基础，得到上述4类属性值及对数正态分布参数取值。当K取200时，4类属性与对数正态分布参数之间聚类结果如图4所示。

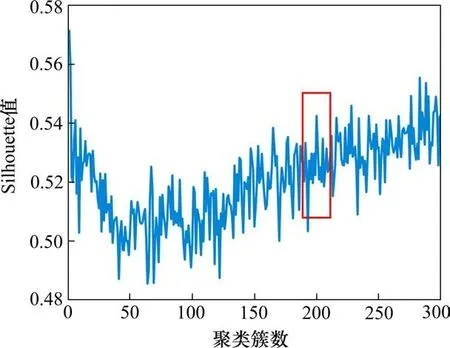
图3 各类silhouette的平均值Fig.3 Average of various silhouettes

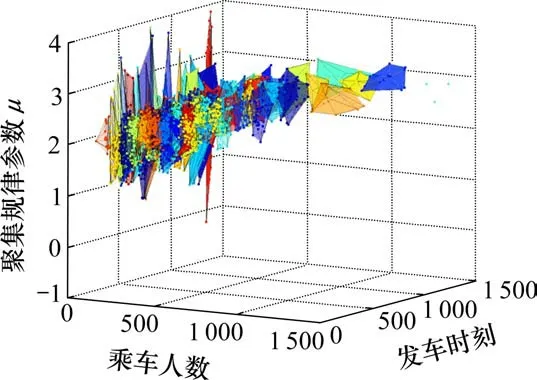
图4 200类属性聚类结果Fig.4 Clustering results of 200 categories of attributes

1.1.2 旅客检票规律

调查广州局集团部分车站候车室发现，旅客携带行李数量、检票熟悉程度及闸机的灵敏度会影响闸机检票速率；客运员对业务熟练程度也会对人工检票速率造成影响[8]。由于旅客的随机性较大，闸机检票速率在5～13人/min，人工检票速率在9～20人/min，故检票口检票速率在60～120人/min，平均检票速率为108人/min。在检票过程中，该车次候车旅客逐渐减少，检票速率逐渐降低，此时检票速率为该列车剩余候车人数：

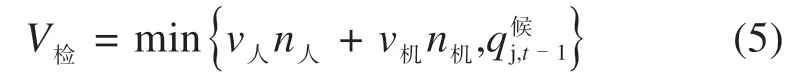
式中：v人为人工通道的检票速度；n人为人工通道的检票个数；v机为匝道机器检票速度；n机为检票匝机个数；为第t-1 min候车厅内乘坐编号为j的列车旅客人数。

1.2 列车乘车人数

将固定乘车人数作为该车站所有列车乘车人数计算最高聚集人数时[9]，与实际结果偏差较大。通过统计广州铁路集团7 426趟不重复列车乘车人数，计算乘车人数与发车时刻、车站属地类型、是否始发、列车类型等属性的Pearson值(如表3所示)，可以发现车站是否有轨道交通衔接、所在地级市的常住人口、发车时刻等属性与列车乘车人数之间具有较强的相关性。当车站具有轨道交通衔接，选择高速列车出行的旅客将会适当增加；车站服务城市常住人口不同，列车乘车人数也会有较大差异；受列车开行方案影响，早于8:00、晚于22:00时间段内乘车人数相对较少。

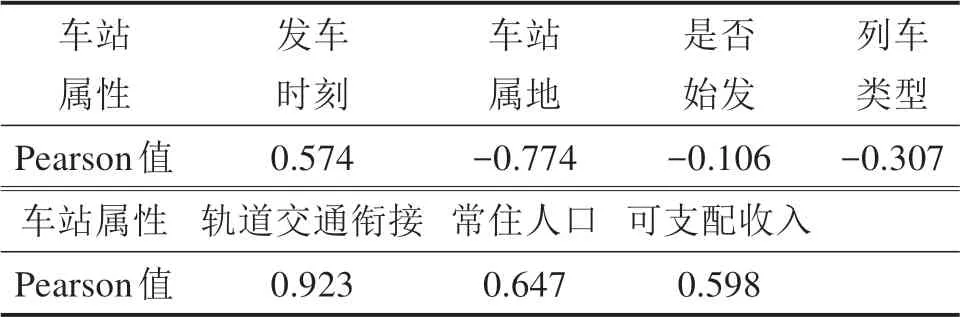
表3 相关属性与乘车人数Person检验值Table 3 Correlation attributes and Person test value of the number of passengers

本文在已有研究的基础上，考虑列车发车时间、车站所在城市常住人口、车站是否有轨道交通衔接等关键因素对列车乘车人数的影响，并用K-means聚类算法和Silhouette测度指标确定各类属性取值及列车乘车人数取值，有助于提高最高聚集人数模型的实用性和准确性。

2 建立旅客聚集仿真模型

通过文献的总结和现场调查可知，列车的乘车人数、车站列车运行图、列车发车时间、检票时间及旅客聚集规律均会影响车站最高聚集人数计算结果[10-15]。新建高速铁路车站列车运行图可以从相似车站得出，故本文以已知新建车站列车运行图为前提，计算该新建车站可能出现的最高聚集人数。由于车站候车室不仅用于旅客候车，部分区域还用于管理维护，最高聚集人数时刻无法准确确定，因此本文通过优化概率法，计算出固定时间间隔内的车站旅客人数，进而得出车站旅客最高聚集人数。

根据旅客聚集规律，在第t时刻乘坐第j列车到站旅客比例为：

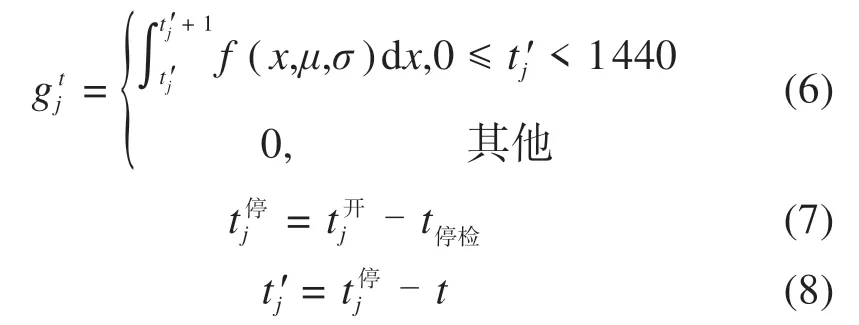
式中：t停检为停止检票时刻与列车发车时刻的时间间隔；t开j为第j列车发车时刻；t停j为第j列列车停止检票时刻；t为全天第t分钟；t′j为距离停止检票时刻的时间(t′j>0);f(x)为对数正态分布；μ，σ为对数正态分布参数，根据聚类结果和距离判别法确定，如式(9)所示；gt j为在t分钟内，第j列车乘客到达人数占该列车总乘车人数比例。

式中：xi为第i个待求参数的车站属性；为第j类中第i个车站属性值；D为聚类结果与待求参数属性的最小距离。

根据列车乘车人数和旅客聚集规律，在第t时刻乘坐第j列车乘客人数为：

式中：Kj为第j列车乘车人数，由聚类结果和距离判别法确定，如式(9)所示；为在t分钟第j列车进站人数；α校正系数为车站内存在站内换乘和铁路职工进站乘车，需对列车乘车人数进行校正，通常取1.01～1.03。

t分钟第j列车候车人数为第j列车上1 min的候车人数加上该列车进站旅客人数，如果该列车在t分钟内开始检票则需要减去t分钟内乘坐第j列车的检票旅客，即

对t时刻内在车站候车旅客进行累计求和，即可得到该时刻车站内的聚集人数为：

以5 min为间隔，对车站候车人数进行累加求得平均值，即可求得候车厅聚集人数：

则该车站最高聚集人数为：

对于新建高速铁路车站，可根据车站设计指标查找已运营的相似车站并近似确定列车运行图，根据车站属地类型、城镇常住人口、车站未来是否规划轨道交通等相关因素确定旅客聚集规律及每趟列车校正乘车人数，由式(6)～式(16)即可计算新建车站未来最高聚集人数，为车站规划提供指导性意见，有助于车站完善设施设备、制定管理对策、提高运营效率。

3 算例检验

根据成都铁路局提供2019年某日成都东站列车运行图，成都东站一天出发的列车数为210列，统计成都东站8:00～20:00共发送列车177列，占全天发送列车的84%，其中8:00～9:00共发送18列列车，为全天最高发送时间段。主要计算步骤如下：

1)收集成都常住人口、城市城镇人口可支配收入、成都东站是否有轨道交通衔接、列车发车时间、列车等级等关键属性，根据式(9)即可从聚类结果(如表4～5所示)中得到成都东站各列列车乘车人数及旅客聚集规律拟合函数参数取值；2)由式(6)即可求出该列车旅客各时刻到站比例；3)根据式(10)～(13)即可求出该列车各时刻站内旅客候车人数；4)根据式(14)～(16)即可计算出该天成都东站旅客最高聚集人数。本文运用Matlab编程得到成都东站旅客聚集人数趋势图(如图5所示)，曲线最高点即为成都东站当天旅客最高聚集人数。

表4 乘车人数与相关因素检索表(部分)Table 4 Number of passengers and related factors analysis table(partial)

由图5可知，实际旅客最高聚集人数出现在14:50，为9 384人；本文最高聚集人数计算模型预测出旅客最高聚集人数出现在10:00，为9 611人，与实际最高聚集人数误差为2.36%；采用固定拟合函数参数和列车乘车人数的最高聚集人数计算模型的峰值出现在12:15，为8 389人，与实际误差达到10.61%。虽然本文计算模型得到的旅客聚集人数峰值与实际存在一定偏差，但旅客聚集趋势与实际旅客聚集趋势相符，且计算结果误差低于现有计算模型，因此本文最高聚集人数计算模型可以更好地拟合车站旅客聚集趋势、更准确地计算车站最高聚集人数。

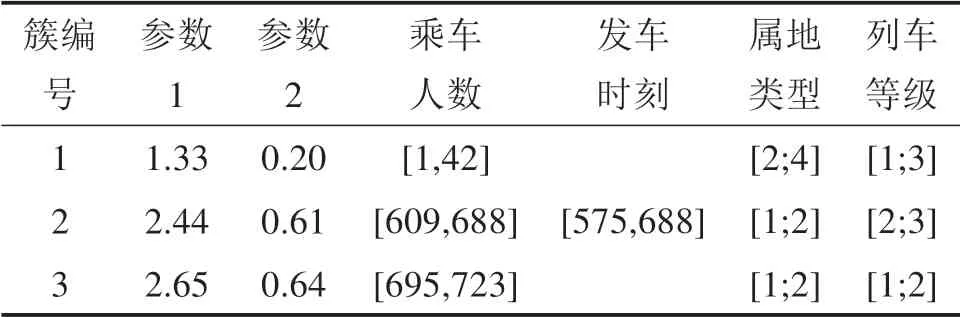
表5 旅客到达规律与影响因素检索表(部分)Table 5 Passenger arrival rules and influencing factors analysis table(partial)

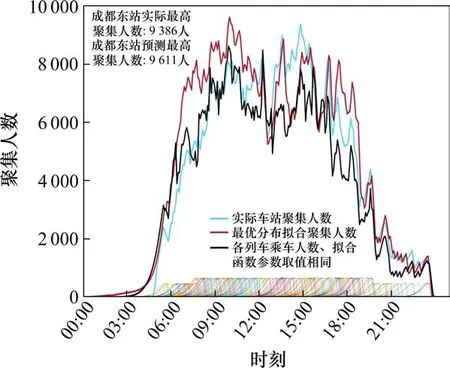
图5 成都东站实际聚集人数与计算聚集人数Fig.5 Actual and predicted number of people gathered at Chengdu east railway station

4 结论

1)以实际车站38 d典型时间段内旅客候车时间为基础数据，相比于文献[1-3]人工统计的数据，数据量更大、精度更高。用对数正态分布、威布尔分布、复合负指数分布、有理函数分布进行拟合，得出对数正态分布拟合效果较好，且对数正态分布参数与车站及列车的属性有较强相关性。

2)在文献[6]的基础上，考虑了发车时刻、车站属地类型、列车类型、城市常住人口、城镇人均可支配收入等属性对旅客聚集规律的影响。用Person检验和Kruskal-Wallis检验，筛选出与旅客聚集规律和列车乘车人数相关性较强的属性，并通过K-means算法得到列车乘车人数和拟合函数参数检索表。

3)以成都东站作为案例，根据成都东站及各列车属性，检索出各列车乘车人数与对数正态分布参数取值，通过计算得到成都东站最高聚集人数为9 611人，与实际最高聚集人数误差为2.36%，且模拟旅客聚集趋势与实际旅客聚集趋势相符，模型模拟效果较好且精度较高。