基于模糊多准则优选的高速兼顾普速线路超高设计

高天赐，李子涵，袁泉，曾文驱，李其龙，何庆

(1.西南交通大学 高速铁路线路工程教育部重点实验室，四川 成都 610031；2.西南交通大学 土木工程学院，四川 成都 610031；3.广州地铁设计研究院股份有限公司，广东 广州 510010；4.中铁第四勘察设计院集团有限公司，湖北 武汉 430063）

随着我国经济的快速发展，高速铁路网已逐步遍及全国大部分地区，为了进一步提升当前路网的运输效率，充分满足不同层次的客流需求，高速铁路开行普速列车已成为解决上述问题的重要方案。然而，由于高速列车和普速列车的通过速度以及动力学性能的不同，二者通过相同曲线半径时，其动力响应也会随之产生较大差异，同时超高的不合理设置也会严重影响二者的运行平稳性[1]，难以同时兼顾高速列车和普速列车对旅客舒适性的要求。因此，需要合理研究高速兼顾普速线路曲线超高的设计，为高速铁路兼顾普速客车上线提供技术参考。一般情况下，铁路新线曲线超高设计时，为了兼顾低速列车的通行，通常采用线路最高设计速度Vmax的0.8倍来计算外轨超高，其计算公式如下：

式中：R为列车通过的曲线半径。这种方法虽然简单，但极易造成线路通车以后各曲线出现欠超高和过超高的情况。

针对铁路曲线超高优化设计的问题，不少学者展开了相关研究[2-11]。其中，涂文靖[2]给出了曲线超高检算中实设过超高、欠超高、超高顺坡率等主要指标的优化设计方案，并通过实车检测验证了优化方法的合理性；胡江民[3]以郑焦铁路开行普速客车曲线超高设计为例，对不同速度组合下的曲线超高进行计算，分析了超高的设置原则，并检算了相应的舒适度；张齐坤等[4]通过回归分析方法，建立曲线超高与旅客舒适度之间的联系，探究了曲线超高对旅客乘坐舒适度的影响规律，并提出了超高参数的取值建议；楼少俊等[5]从轮轨接触关系的角度进行分析，提出设置曲线大欠超高和小过超高的观点，并将其进行量化，方便现场操作；POWELL[6]根据现场实验，分析了不同运营速度超高设置与轮轨力的关系，发现曲线超高对轮轨横向力以及轮轨磨耗存在较大影响；龙建兵等[7]根据城市轨道交通不同曲线工况，提出单一速度模式采用平均速度法，多种速度模型采用优化的接近高速法来选择超高的限值；孔凡兵[8]基于规范对地铁超高的规定，探讨了运行速度在120 km/h条件下，曲线最大超高值设定为150 mm的必要性；刘磊等[9—10]对350 km/h以及400 km/h高速铁路平面线形进行研究，并提出了合理的曲线半径和相应的曲线超高设计值；GAILIENĖ等[11]针对双轨式轨道的运行舒适性展开分析，提出了双轨式轨道曲线外轨超高设计的理论计算方法。综合上述文献调研不难发现，目前关于高速兼顾普速线路曲线超高值设计的研究相对较少，并且现有的研究方法大多以理论计算和实车检测为主，缺乏相应的动力学仿真计算和多目标优化理论的分析。鉴于此，本文基于多刚体动力学理论[12-15]，建立车辆—轨道耦合动力学计算模型，结合模糊多准则优选理论[16-18]，以高速及普速列车运行舒适性Sperling指标作为优化目标，以通过相应曲线半径的过超高和欠超高作为约束条件，构建基于模糊层次分析法的高速兼顾普速线路曲线超高的多准则优选模型，为高速铁路兼顾普速客车上线提供参考依据。

1 模型介绍

1.1 车辆-轨道耦合动力学模型

为了探究不同曲线超高对列车舒适性的影响，本文利用UM多体动力学软件建立关于高速列车和普速列车的车辆-轨道耦合动力学模型(图1)，车辆模型主要由车体、转向架、轮对以及轴箱等多个刚体组成，其中轮对与转向架通过一系悬挂相连接，转向架与车体通过二系悬挂相连接且二者之间设置了抗蛇形减振器与抗侧滚扭杆装置，进一步防止转向架出现蛇形失稳。此外，在轮轨耦合接触部分，采用Hertz非线性弹性接触理论计算轮轨法向力，进一步以Hertz接触理论为基础，采用Kalker简化理论及其数值算法FASTSIM计算轮轨的切向蠕滑力及蠕滑力矩。由于本文重点分析曲线超高对列车运行舒适性的影响，因此未考虑轨道结构以及下部基础的影响。

图1 车辆-轨道耦合动力学模型Fig.1 Vehicle-track coupling dynamic model

1.2 Sperling指标

列车通过曲线时欠超高和过超高主要由旅客的横向舒适度控制[2,4]，为了更加深入准确地对列车的运行舒适性进行评价，仅考虑车体振动加速度的大小是不够的，还要考虑列车振动的频率，而Sperling指标[19]就是根据列车车体的振动频率来对列车的舒适性进行评价，因此本文选择高速列车和普速列车的Sperling指标作为优化目标来设计曲线的超高值，同时将安全性指标(包络轮轨力、轮重减载、脱轨系数等)作为限制，防止在设计超高值影响列车行车安全。Sperling指标的计算公式[20]如下：

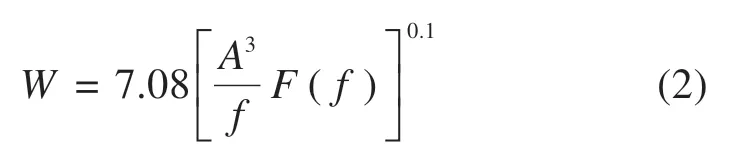
式中：A为车体振动加速度，g；f为振动频率，Hz；F(f)为频率修正系数。

由于列车的速度和频率都在随时间变化，因此，评定时要将加速度的波形按照频率进行分组，根据每组的频率和加速度来计算该组的平稳性指标Wi，总体的平稳性指标计算如下：

式中：N为加速度波形的分组总数。Sperling指标越大，表明列车运行的舒适性和平稳性越差。

1.3 模糊多准则优选理论

设有n个目标函数g1(x)，g2(x)，…，gn(x)在x∈S时存在最优解，S为可行域。在本研究中，目标函数有2个，分别为高速列车和普速列车通过曲线时的舒适性Sperling指标，即g1(x)=-Sperling 1，g2(x)=-Sperling 2，S在本研究中为超高的取值范围。根据极大极小的决策原则，多准则优选问题可按照如下表述：

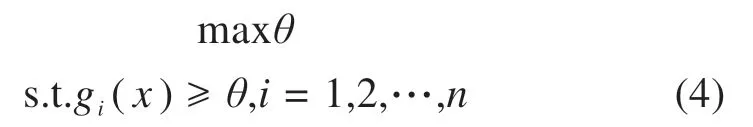
其中：θ为gi(x)在限制条件内的最小值(由于Sperling指标越小，列车舒适性越好，因此在本研究中，θ可表示为Sperling指标的倒数)。在进行模糊多准则优选时，通常将容许度和期望值构成的目标隶属度函数δi(x)作为模糊优化目标。δi(x)为决策的满意度，其值越大，表明所需优化的目标函数值越接近于最优解。因此，可将上述优化问题重新表述为：

设xi(1≤i≤n)使函数值gi(x)达到最优解，则各目标的期望值g*i为：

在计算某目标容许度时，将其余子目标理想最优解在该目标中对应函数值的最小值作为容许度极限值[21]：

在计算隶属度函数时，采用线性结构，则各目标的隶属度函数可表示为：

在模糊优化中，希望目标函数值大于或等于目标的期望值，且能容许在(gi,min,g*i)范围内小于g*i。

同时，本文引入模糊层次分析法，可通过两两对比来判断多子目标函数的关键程度。对比结果可被分为5个不同等级，并用三角模糊数来进行量化分析，按照重要程度设定约束条件。此外，考虑到超高优化过程中存在过超高h[g]以及欠超高h[q]的约束，则多准则优选模型可表达如下：

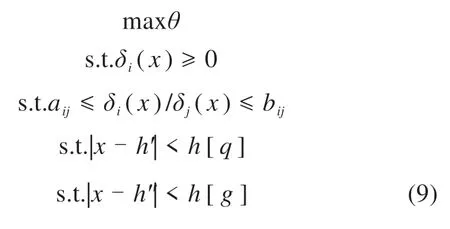
式中：h′和h″分别为高速列车以及普速列车通过曲线时的均衡超高。aij和bij分别表示第i个目标函数与第j个目标函数重要程度的对比结果，即普速列车和高速列车运行舒适性重要程度的对比，二者的取值原则如下：

1)第i个目标函数与第j个目标函数同等重要：aij=1,bij= 3；

2)第i个目标函数比第j个目标函数稍微重要：aij=1,bij= 5；

3)第i个目标函数比第j个目标函数明显重要：aij=3,bij= 7；

4)第i个目标函数比第j个目标函数强烈重要：aij=5,bij= 9；

5)第i个目标函数比第j个目标函数极端重要：aij=7,bij=9。

2 最优超高值的具体确定步骤

针对高速铁路兼顾普速客车上线的曲线超高设置，本文将模糊多准则优选理论与车辆—轨道耦合动力学理论相结合，其计算流程如图2所示。

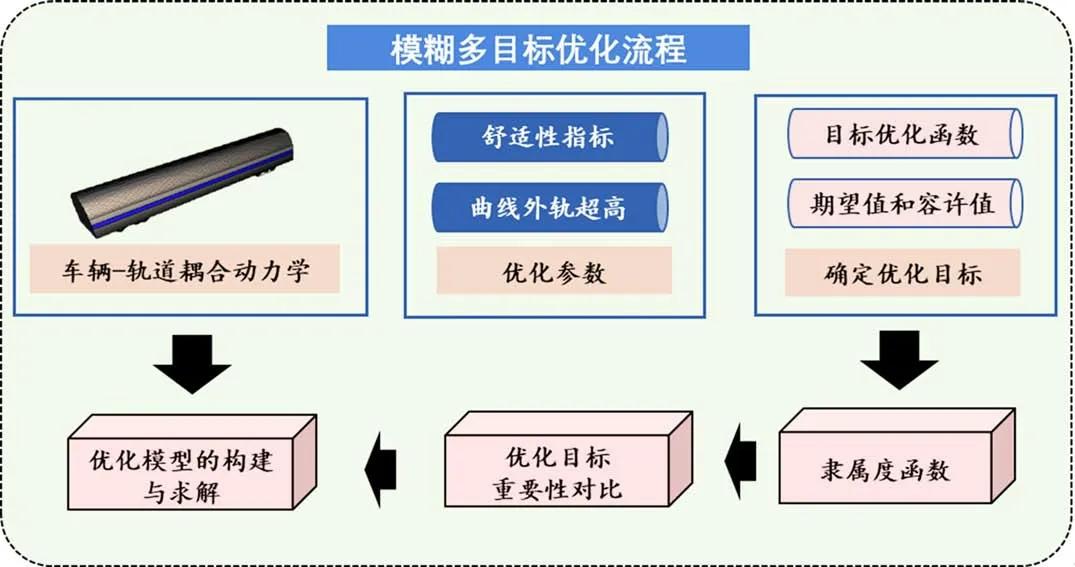
图2 多目标优化模型计算流程Fig.2 Calculation process of multi-objective optimization model

1)分别以高速列车和普速列车的Sperling指标最低作为优化目标，以高速列车的欠超高h[q]允许值和普速列车的过超高允许值h[g]为关键约束条件；

2)建立车辆—轨道耦合动力学模型，分别计算高速列车和普速列车通过不同曲线外轨超高(h,h为5 mm的整数倍)时的Sperling指标；

3)根据步骤2的计算结果，得到高速列车和普速列车各自对应的最优超高值(H*i,i=1,2)及其目标函数值(gi(H*i),i=1,2)，并根据式(6)～(7)确定高速列车和普速列车的期望理想解和容许度；

4)基于线性结构计算各目标的隶属度函数δi(h)；

5)对比各目标的重要程度，根据模糊层次分析法确定各目标的比例标度(aij,bij)；

6)根据式(9)及步骤1中引入的关于超高允许值的关键约束条件建立多准则优选模型；

7)遍历搜索所建立的模糊多准则优选模型的可行解，得到最优的超高设计值H*。

3 计算实例分析

以半径6 000 m的曲线作为计算实例，基于动力学仿真分析，将通过该曲线的高速列车(250 km/h)和普速列车(160 km/h)的横向舒适度Sperling指标作为优化目标，对曲线外轨超高进行设计。图2(a)～2(b)分别为高速列车和普速列车通过半径为6 000 m曲线时Sperling指标的仿真结果，由图可知，高速列车和普速列车分别在超高为125 mm和55 mm的情况下，横向Sperling指标得到最优解(最小值)，同时，二者的均衡超高分别为122.9 mm，50.34 mm，其动力学仿真结果与理论计算结果相近。此外，不难发现高速列车和普速列车所对应的最优超高值存在较大的差异，从直观上难以选择合适的超高值，使其能够同时满足2种类型列车对舒适度的需求。

图3 高速列车与普速列车Sperling指标计算结果Fig.3 Results of Sperling index for high speed train and ordinary speed train

因此，本文基于模糊多目标优化理论，以二者的舒适性Sperling指标的最小值作为优化目标，定义目标函数g1(h)=-Sperling 1,g2(h)=-Sperling 2，其中h为曲线外轨超高值，Sperling 1为高速列车的舒适性指标，Sperling 2为普速列车的舒适性指标。各目标函数的期望值与容许度极限值如表1所示。

表1 各目标最优解函数值Table 1 Optimal value of each objective function

由式(8)建立高速列车舒适性的目标隶属函数：

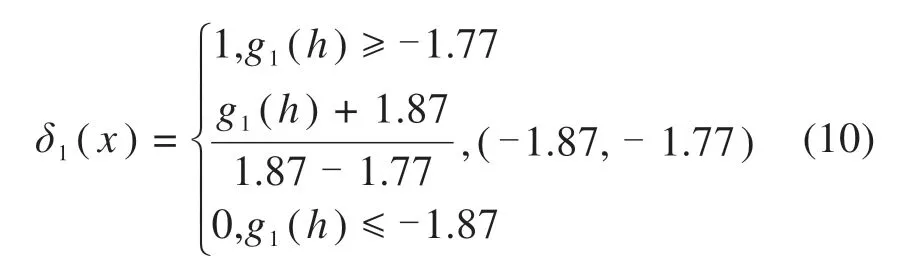
普速列车舒适性的目标隶属函数：

由于本文的研究对象为高速兼顾普速线路，因此高速列车的舒适性相比于普速列车稍微重要，并且最终得到的超高最优解必须满足规范中过超高和欠超高的允许限值[22-23]，则曲线外轨超高值的模糊多目标优化模型可表示为：

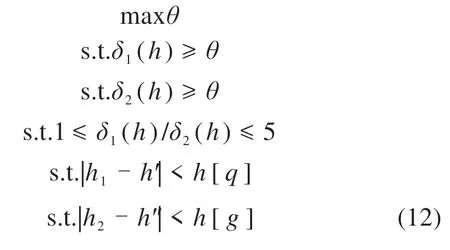
式中：h′和h″分别为高速列车以及普速列车通过曲线时的均衡超高，本案例中二者分别为122.9 mm和50.34 mm；h[q]为高速列车欠超高允许值，为40 mm；h[g]为普速列车过超高允许值，为70 mm。

最终，通过编程遍历搜索可行解可得到最优超高值：h=85 mm，此时，对应的高速列车和普速列车Sperling指标分别为1.78和1.23，θ为0.83，欠超高和过超高值分别为37.9 mm和34.7 mm，满足规范要求。同时，在最优超高值下的各项安全性指标均未超限，不会影响行车安全。此外，按照传统超高的设计方法(式(1))，得到的超高值为80 mm，其所对应的欠超高值和过超高值分别为42.9 mm和29.7 mm，可以发现此时的欠超高值已经出现超限的情况。因此，相比于传统的设计方法，本文的超高设计方法更加合理。

表2进一步地，计算了不同曲线半径下高速兼顾普速线路的曲线超高最优值，可以发现，当曲线半径为4 000 m时，高速列车的欠超高值和普速列车的过超高值均接近到限值。因此，当曲线半径小于4 000 m，无论曲线外轨超高如何设置，高速列车的欠超高值和普速列车的过超高值均无法满足规定的要求，进而可知高速(250 km/h)兼顾普速(160 km/h)铁路的最小半径应设置为4 000 m。

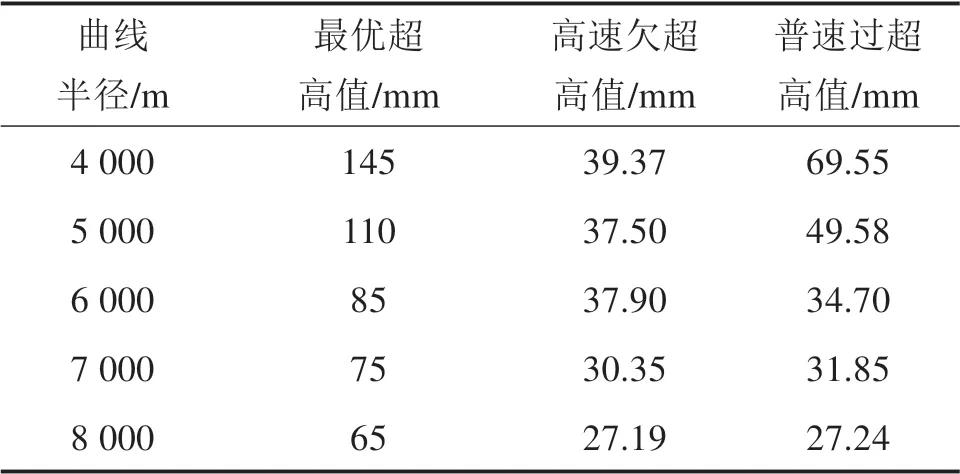
表2 不同曲线半径最优超高值计算结果Table 2 Results of optimal superelevation with different curve radius

4 结论

1)基于车辆—轨道耦合动力学理论计算高速及普速列车的动力响应，采用模糊多目标优化算法对高速列车和普速列车的运行舒适性Sperling指标进行优化，以通过相应曲线半径的过超高和欠超高作为约束条件，建立基于模糊层次分析法的高速兼顾普速线路曲线超高的多准则优选模型。

2)本文采用的方法能够同时兼顾高速列车和普速列车的舒适性，并满足规范中关于过超高和欠超高的允许限值，可为高速铁路兼顾普速客车上线提供技术参考。