多式联运网络关键节点识别及性能分析
——以珠江西江经济带多式联运网络为例
冯芬玲,许天鸿
(中南大学 交通运输工程学院,湖南 长沙 410075)
随着我国多式联运的快速发展,近年来多式联运作为交通运输业向物流现代化转型的主要方面,承担着降本增效的重要角色。对多式联运的网络构建和网络运行分析进行研究,结合多项指标,识别网络中的关键节点,并对网络节点失效后的性能变化趋势做出判别,有利于确定多式联运环节中的关键地区和路径,并对其安全运行和后续发展提供参考。许多学者对于复杂网络在交通网络中的应用展开了深入研究。对于轨道交通网络,张晋等[1]基于复杂网络理论,对北京地铁拓扑结构进行了研究,指出少数关键节点的失效即会对整个网络造成较大冲击,这一点在本文的研究中得到了进一步证实,对于多式联运网络而言,少数关键中转节点的失效就会造成整个网络效能的大幅下滑;YANG等[2]认为,节点的重要度取决于节点度和节点介数等主要指标;于宝等[3]在YANG等人的基础上,构建了节点重要度评价体系,并对我国高速铁路网络的运行效率和脆弱性进行了深入研究;对于交通网络的拓扑表述方法,一般使用L型空间[4-5]、P型空间等表述方法[6-7];对于货运网络拓扑结构特征或关键节点识别的研究中,ZENG等[8]对工程大件运输网络优化及抗毁性展开研究,并对该类型的货运网络的拓扑特征指标、体现网络性能和抗毁性的相关指标给出了定义,其对大件物流过程中运输网络的拓扑结构指标以及网络抗毁性进行了分析,指出网络节点重要度的研究需要全面考虑实际情况下的运输任务、地理特征等指标,为本文的重要度综合评价体系构建提供了参考。种鹏云等[9-11]对于货物运输网络的抗毁性测度分析进行了研究,提出通过给网络中边附加风险、流量等权值的方式,对节点失效后带来的运输能力损失和风险增加进行了仿真分析。本文结合前人研究内容基础上,展开对多式联运复杂网络的构建与拓扑结构特征研究,建立考虑多因素的节点重要度综合评价体系,模拟蓄意攻击与随机攻击,讨论节点失效后网络性能的变化趋势,从而弥补多式联运网络结构与性能分析研究中的空白,为多式联运拓扑结构的优化与网络的规划建设提供参考依据。
1 珠江-西江经济带多式联运网络构建及拓扑特征分析
在珠江西江经济带的多式联运网络中,共有11个地区,符合复杂网络中的P型空间,即换乘空间。对多式联运而言,其网络表述在节点定义、链路存在的条件等都较为符合,即站点、港口、枢纽等为网络节点,若2个节点间有直达交通线路,两者间就存在链路。基于此构建线路网络模型,由不同运输方式和路径构成的网络构成了复杂网络G,多式联运网络G示意图如图1所示。

图1 珠江西江经济带多式联运网络示意图Fig.1 Schematic diagram of multimodal transport network in the Pearl River Xijiang Economic Belt
由于每个地区在网络中可能承担公路、铁路、水运节点中的一个或多个,基于此,本文对11个地区进行了节点划分,使用“Guangzhou”,“Guangzhou 1”,“Guangzhou 2”3类节点,分别代表广州的公路、铁路、水运节点。不同地区的同类节点,经过相应运输方式的路径连接。除此之外,由于3个节点间的换装、转运过程产生了成本,所以每个地区3个节点两两连接形成的边为“虚边”,代表不同运输方式间中转换装的过程;每个节点按照相应的运输方式与其他地区的同一运输方式的节点连接形成的边为“实边”,代表相应运输方式的实际运输路径,节点设置如表1所示。

表1 珠江西江经济带多式联运网络节点设置Table 1 Node setup of multimodal transport network in the Pearl River Xijiang Economic Belt
对该复杂网络的各项静态指标进行计算和统计,所使用的计算公式如表2所示。其中,由于多式联运网络中完成运输任务需通过多个车站(节点)及多种运输方式的运输路径(边),因此所有介数中心度之和远小于1,因此本文使用文献[12]提出的标准化介数作为反映节点使用频繁度的指标。

表2 指标计算公式Fig.2 Index calculation formula
其中,aij为邻接矩阵变量;ki为节点度;Bi为标准化介数;dij为节点i到j的最短路径;Ci为聚类系数;Ei为节点i的相邻节点;γ为点连通度,eG为网络的边数;eGmax为网络G的最大边数;D为平均路径长度;E(G)为网络效率;q为自然连通度;qi为邻接矩阵特征根。
利用Python编程计算,对构建出的复杂网络G求解各项指标,可以得到该网络由29个节点,57条边组成,平均度为3.931 0,网络介数为0.063 4,网络效率为0.001 734;连通度为2.294 8。该网络平均最短路长应用了Dijkstra算法求出其加权平均最短路长,为379.45,权重设置为实边的地理距离。由于网络效率与平均最短路长的倒数呈正相关,因此网络效率值较低。
2 珠江-西江经济带多式联运网络关键节点识别
在多式联运的运输环节中,如果发生突发情况,会导致某些中转作业节点失效,或是某种运输方式无法完成运输任务,关键节点和关键边的稳定运行将最大程度保证多式联运网络的平稳运营,因此有必要对网络中的关键节点进行识别研究,进一步提高网络性能分析的精度。
2.1 节点重要度评价体系构建
在传统的节点识别研究中,研究人员通常使用节点介数、节点度、点连通度、补图效率(节点失效后形成的补图网络效率)作为拓扑结构或脆弱性指标进行重要度分析和排序。在本文研究的复杂网络G中,按节点分布的上述指标数据如图2所示。

图2 节点各项指标Fig.2 Distribution of node indicators
传统的节点重要度评价方法存在一定的不足,取节点失效后形成的补图效率与原网络效率变化率最大的前15个节点,如表3所示。例如节点1(广州—公路枢纽)和节点28(玉林-铁路枢纽)的节点度仅为3和1,且节点28的介数仅为0.049 050,但是这2个节点失效后,网络整体的效率下降程度达到了15.67%和12.06%,这意味着这2个节点也需要重点预防和维护。

表3 变化率最大的前15个节点(部分)Table 3 Top 15 nodes with the largest rate of change(partial)
在以往的节点重要度评价方法[13]中,由于出发点仅包括网络本身的性能指标,并不能全面地识别关键节点。为建立完备的节点重要度评价指标体系,选取的指标需要有一定的科学性、代表性和全面性,不仅要反映节点在网络中的拓扑结构重要性,还要联系网络所处经济带中多式联运网络这一实际线路网,从而体现出运输节点集散货物、连接其他运输方式进行中转换装作业的关键性。
因此本文选择相应的指标构建节点重要度综合评价体系,完成节点重要度的选取与排序。评价体系的参考指标为补图效率变化率y1;1级指标为w1拓扑结构,其中包括2级指标x1节点度和x2节点介数;w2脆弱性,包括x3连通度;w3货运能力,包括x4货运量;w4发展指数,包括x5基础设施能力指数和x6第三产业及工业产值。
其中,x1,x2与x3指标数据已计算完成;代表货运能力的x4货运量(t),由该节点相应运输方式的年货运量构成;x5基础设施能力指数由该节点的枢纽换装作业设施设备以及作业能力百分制打分构成;x6是该地区的GDP构成中第三产业及工业产值(万元)数据。指标数据汇总如表4所示。

表4 指标数据汇总(部分)Fig.4 Summary of indicator data(partial)
2.2 关键节点的识别与分析
为了避免单一模型评价时出现的指标权重误差,本文使用随机森林回归和灰色关联度2种分析方法,以补图效率变化率为参考指标,得到各项指标的权重值,最后求取2种方法的平均权重实现节点重要的综合评价。
2.2.1 随机森林
科学家Breiman在2001年提出的随机森林是一种新型机器学习算法,通过重采样技术从原始样本中有放回地抽取多个样本,形成新的样本集。对每个独立抽取的样本用加权均值训练一个决策树(弱预测器),生成n个决策树,形成森林(强预测器),根据所有决策树预测的平均值得到最终预测结果。其主要特点是对数据类型及分布没有要求,预测的结果精度较高,并且具有防止出现数据过拟合等优点[14]。
利用Python中sklearn库,编程实现节点重要度评价模型的构建,以补图效率变化率指标为因变量y1,指标数列x1到x6为自变量。当训练样本的比例为0.3,随机状态(random_state)固定为10时,训练效果较好。经过计算,指标排序与指标权重结果为:1)连通度,权重为0.219 263;2)节点介数,权重为0.195 867;3)节点度,权重为0.152 535;4)第三产业及工业产值,权重为0.152 327;5)基础设施能力指数,权重为0.148 147;6)货运量,权重为0.131 862。
2.2.2 灰色关联度
灰色关联法作为衡量因素之间发展趋势相似或相异程度的评价方法,可综合评价多指标问题。本文利用灰色关联法,将各项指标与参考指标的关系进行排序,并求出相应指标的权重[15]。
利用Python中pandas库,编程实现节点重要度评价模型的构建,以补图效率变化率指标为参考数列y1,指标数列x1到x6为比较数列。首先对指标数列进行初值化处理,计算灰色关联系数与关联度,最终将关联度转化为待分配的权重,得到指标排序与关联系数结果为:1)基础设施能力指数,权重为0.896 707;2)连通度,权重为0.862 5;3)节点度,权重为0.825 904;4)节点介数,权重为0.776 031;5)第三产业及工业产值,权重为0.741 638;6)货运量,权重为0.718 408。
将x1到x6的灰色关联系数归一化得到相应的指标权重数据依次为:1)基础设施能力指数,权重为0.185 993;2)连通度,权重为0.178 898;3)节点度,权重为0.171 307;4)节点介数,权重为0.160 963;5)第三产业及工业产值,权重为0.153 829;6)货运量,权重为0.149 011。
2.2.3 节点重要度计算与排序
对2种方法得到的结果求平均值,从而避免一种模型和一种评价结果单一性和局限性。得到最终的权重并对节点进行重要度排序,取前15位重要节点,得到排名如表5所示。

表5 重要度排序Table 5 Importance ranking
由综合评价结果可知,复杂网络G的拓扑结构特征指标与综合排序十分吻合,指标w1与w2排序靠前的节点需要加强维护和防范。但是节点13(南宁公路枢纽)、节点23(深圳铁路枢纽)与节点26(梧州水运枢纽)等节点在该网络中同样承担着重要的作用,有效完成了货物的集疏运与中转换装等任务,在多式联运运输过程中地位同样十分重要。
3 多式联运网络模拟攻击与性能分析
3.1 网络性能指标
网络性能指标反映了网络运行时的相关能力,这些指标会随着节点或边的失效整体呈现下降的趋势,体现在网络的鲁棒性、可靠性、抗毁性、脆弱性等性质上,这些指标相互独立,但是又互相补充,存在一定联系。因此研究这些关键指标的变化,对于衡量复杂网络的性能十分必要。
本文将对复杂网络G模拟蓄意攻击与随机攻击导致相应节点失效的方法来验证和研究网络性能指标的变化趋势,蓄意攻击通常指有目的的人为破坏关键节点;而随机攻击是指网络节点遭遇的不确定意外事故,如运载工具故障、恶劣天气环境、自然灾害等重大突发事故。蓄意攻击将按照表5中节点重要度综合评价排序的结果,按照次序使重要度为前15名的节点依次失效;随机攻击主要体现不确定性,本文将对29个节点编号生成随机序列依次攻击。在节点损坏后,与该节点相连的边同时将失效,即去除了该节点的邻接关系,形成孤立的点。
描述节点损坏后网络性能的指标通常包括网络效率、网络连通度、最大连通子图、自然连通度等,其中网络效率和连通度反映网络效用情况和连通情况,最大连通子图和自然连通度反映网络的抗毁性及网络整体工作性能。其中,网络连通度、网络效率、自然连通度的指标计算公式为式(4),式(6)与式(7),最大连通子图指标代表网络分解出的子图中,包含节点数最多的子图的节点数。
在模拟后的网络性能指标分析中,为了直观地反映在模拟中各指标的连续变化,将上述指标的变化率作为统一呈现方式,从而使多指标能够同时反映在一张趋势图中。
3.2 蓄意攻击下网络性能指标变化
结合前文所提及的复杂网络G关键节点识别方法,运用节点重要度综合评价与反映网络性能的相应指标,观察按排序进行攻击的节点依次失效后各指标的变化情况。具体步骤如下:1)选取重要度排序前15位的节点作为失效次序,如表9所示。2)按照该顺序依次攻击相应节点,即依次移除重要节点。3)依次计算节点失效后的各项指标数据。4)绘图分析网络性能的变化趋势,得到结论。
按照排序,对网络进行蓄意攻击,使重要节点依次失效,默认初始性能为100%。累计攻击15次的情况下,网络性能的指标随攻击次序的变化情况如图3所示。
由图3中可以看出,除自然连通度之外,另外3项指标的变化趋势并不随着攻击次数的增加而稳定下降。由于首先攻击了重要度较高的节点,因此图3中网络效率与网络连通度指标的下降速度较快,在节点1(广州公路枢纽)、节点3(广州水运枢纽)2个节点失效后迅速下降至初始性能的70%左右。
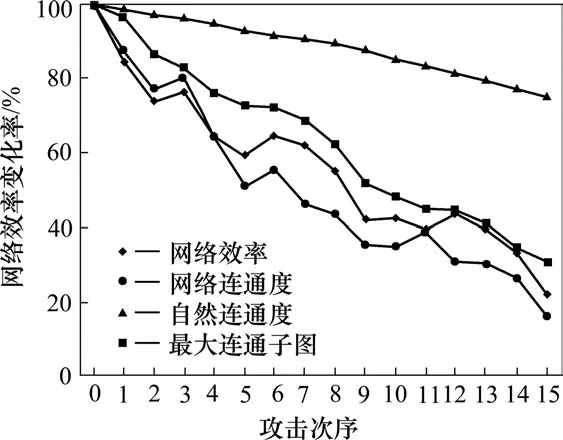
图3 蓄意攻击下网络性能变化Fig.3 Network performance changes under deliberate attacks
在节点22(深圳公路枢纽)、节点2(广州铁路枢纽)等共计5个节点失效后,网络效率和网络连通度即分别下降到了初始的60%和50%;而随着后续攻击中,节点重要度的下降,网络性能的下降速度也随之变慢,在11个节点失效后,网络效率、网络连通度、自然连通度均下降至初始的40%左右。而自然连通度的下降趋势较为平稳,随着攻击次数的增加而匀速下降。
3.3 随机攻击下网络性能指标变化
在随机攻击的环境下,网络性能的各项指标变化情况如图4所示。

图4 随机攻击下网络性能变化Fig.4 Network performance changes under random attacks
从图4中可以看出,随机攻击下的网络效率与网络连通度变化趋势呈现同样的随机性,但是在重要节点失效后,2项指标随之出现大幅度下滑的变化,这一点验证了网络性能的下降会随着重要节点的失效而加速。与蓄意攻击带来的网络性能变化相比,随机攻击下的网络性能衰减速度较慢,网络效率指标在随机攻击22次后下降至初始的40%,而蓄意攻击次序达到13次即网络效率即低于初始的40%。这同时意味着在重点防范和维护了关键节点后,网络中节点随机失效时整体性能下降趋势将减慢,具有一定抗毁性。
4 结论与展望
4.1 研究结论
1)通过构建多式联运网络G,得到珠江—西江经济带多式联运网络的相关指标,包括网络平均度(3.931 034)、网络介数(0.063 4)等拓扑结构特性指标以及网络效率(0.001 734)、网络连通度(2.294 887)、自然连通度(0.610 813)等性能指标。这些指标反映出多式联运网络中各节点的连通度、重要节点负载过大等问题,可为后续多式联运的建设发展与规划调整提供参考。
2)通过构建网络关键节点综合评价体系,对网络中关键节点进行综合评价和排序后,发现节点13(南宁公路枢纽)、节点23(深圳铁路枢纽)与节点26(梧州水运枢纽)等节点虽然在网络拓扑结构特征指标排序不够靠前,但是由于其货运能力强、发展机会好等因素,同样处在综合评价排序的前列,这些关键节点同样需要重点防护。
3)通过模拟蓄意攻击和随机攻击,使网络中节点失效,并分析网络性能指标变化趋势。发现网络效率和网络连通度会随着关键节点的失效出现大幅下降,在蓄意攻击和随机攻击2种情况下其变化趋势都验证了这一结论;最大连通子图的下降趋势较为稳定,但是也会随着失效节点的数量到达一定程度时,出现大幅下滑;而在蓄意攻击中,自然连通度的下降速度较为稳定,而随机攻击情况下,该指标的下降速度会随着失效节点数目的增多而加快,呈现凸函数的特征。
4.2 展望
本文实现了对多式联运网络拓扑特性以及关键节点识别的实证和理论建模研究,相关研究成果也从风险、安全性、可靠性等方面逐步深化了对多式联运等货运网络交通系统运行机理的认知,但要满足多式联运网络化运营、一体化衔接中转等,对网络中实际货流的分配、网络层间耦合度、网络可靠性优化等方面仍有大量的研究工作有待开展。

