利用MSPSO优化的Duffing-SR检测高铁轴承复合故障
刘小峰,曾伟业,柏林,孔德斌,王明迪
(1.重庆大学 机械与运载工程学院,重庆 400044;2.上海空间推进研究所,上海 201112;3.上海空间发动机工程技术研究中心,上海 201112)
作为高速列车走行部件的核心部件,轴箱轴承长期处在高速动载的服役环境中,容易产生裂纹、剥落、点蚀等各类故障,引起轴温报警,导致列车紧急停车,影响线路正常运行,诱发列车失稳问题[1]。列车轴承的故障诊断对保证列车行驶安全具有重要的研究意义。目前在列车轴承故障诊断方法的研究主要集中在2个方面:1)结合多维故障特征的提取与人工智能网络,通过样本学习方法进行故障的自动识别,例如循环相关熵-支持向量机[2]、变分模态分解-多尺度卷积神经网络[3]、稀疏分类融合法[4]等;2)采用信号处理方法对振动信号进行解调分析,对故障频率进行识别,如自适应噪声互补集成经验模态分解[5]、奇异值分解-共振稀疏解调[6]、形态滤波解调法[7]等。由于轴箱轴承故障试验难度与危险性,能够获得的故障数据不充分、不完整,且受到模型参数优化的制约使得基于故障样本的网络学习方法在工程实践中受到了很大的局限性。传统的基于共振频带解调及其相关优化算法虽然采用EMD消噪、奇异值分解、小波分解等方法在一定程度上削弱了激扰和随机噪声的影响,但轴箱部件间的相互耦合作用使得轴箱轴承的振动信号异常复杂,早期故障频率在解调谱中仍难以识别。杜芬随机共振(Duffing Stochastic Resonance,Duffing-SR)系统描述了当非线性系统的各项参数与输入信号和噪声强度之间存在某种匹配关系时,系统就能将噪声能量转换为信号能量,从而提高输出信噪比(Signal to noise ratio,SNR)的现象。Duffing-SR是一维DR向二维Duffing模型的拓展,其产生的输出信号信噪比高于传统的一维SR系统,由于强噪声背景下加入了阻尼比概念,增强了模型在各类噪声强度下的适应能力[8]。与传统SR一样,Duffing-SR系统的输出结果对参数比较敏感,不合理的参数设置往往会降低共振效果,造成虚假信息对微弱目标信息的遮蔽掩盖。如何实现系统参数的自适应调节是解决SR实际工程应用的关键。为了对SR系统的多个参数进行同步优化,许多研究者采用了萤火虫[9]、人工鱼群算法[10]、遗传算法[11]、差分头脑风暴优化算法[12]、粒子群算法[13]及灰狼优化算法[14]等群智能算法设计自适应随机共振系统,但这些优化算法存在参数搜索效率低,收敛速度慢的缺陷。粒子群优化算法(Particle Swarm Optimization,PSO)作为一种多变量全局优化方法,没有遗传算法的交叉、变异,因此效率高,速度快,具有很强的工程实用价值[15]。值得注意的是,采用粒子群优化的SR系统进行轴承故障检测时还面临着几个问题:1)传统的SR系统优化算法通常以信噪比为自适应函数,无法最大化地凸显轴承故障冲击特征,且尚未考虑强弱冲击间的遮蔽干扰效应;2)优化算法中的粒子搜索处于“半盲目”状态,易造成算法早熟收敛陷入局部最优,造成优化后的SR系统对故障频率的检测失效。针对以上问题,本文以凸显轴承故障冲击特征的加权峭度与目标检测频率处SNR相融合的综合指标作为SR系统的目标函数,采用多尺度简化粒子群优化(Multi-scale Simplified Particle Swarm Optimization,MSPSO)算法,自适应确定变尺度杜芬随机共振(Duffing Stochastic Resonance,DSR)系统的最优结构参数,并对高速列车轴箱轴承的复合故障进行诊断。
1 变尺度杜芬随机共振
为了使DSR系统能检测任意频率、任意幅值的信号,通过频率尺度R和幅值变换系数ε将高频大幅值信号变换为一个符合双稳共振的低频小幅值信号,然后对低频小幅值信号进行共振,识别其特征信号成分。假设输入信号由噪声n(t)=与微弱周期信号u(t)=Acos(2πf0t)组成,其中D是噪声强度,g(t)是均值为0方差为1的高斯白噪声。在该输入信号作用下的变尺度DSR方程为:
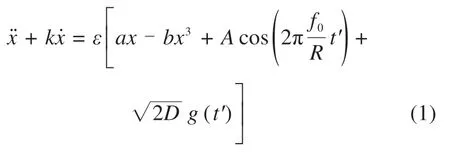
式中:k是阻尼比;x是系统输出;a和b是非线性系统结构参数;g(t′)为交换后的噪声,具有与g(t)相同的分布特性。系统势函数拐点和极点为同一点时,获得系统临界值为Ac=4a3/27b。当噪声的部分能量转移到微弱信号中,在噪声的协助下微弱周期信号的幅值大于Ac,势函数的双稳结构暂时破坏,势垒短暂消失,粒子越过势垒以微弱周期信号的频率在两势阱间实现大范围的跃迁时,系统达到阱间随机共振状态。当噪声能量不足以使周期信号幅值越过Ac且粒子以周期信号的频率在其中一个势阱里面做小范围振荡时,系统处于阱内随机共振状态。DSR系统的实现主要包括2个方法,一是对a,b,k同步寻优,二是确定用来评估系统参数产生效果的测试指标。
2 多尺度权重简化粒子群算法
2.1 简化粒子群
PSO优化问题的可行解可被抽象为D维搜索空间中的一个具有速度信息的粒子的位置。简化粒子群(Simplified Particle Swarm Optimization,SPSO)将粒子更新公式合二为一,对粒子的位置直接进行更新迭代,假设粒子群大小为N,第i个粒子的位置为Xi(k+1),i=1,2,…N,当前搜索得到的个体最优解为Pbi(k)以及整个种群迄今为止搜索到的全局最优解为Gb(k),则粒子位置的更新模型为:

其中:k为当前迭代次数;c1,c2为学习因子,通常取为 2;r1,r2为介于(0,1)之间服从均匀分布的随机数。ω为权重系数,起着平衡SPSO全局寻优和局部寻优能力的作用。
2.2 多尺度SPSO
目前,PSO算法改进策略大部分是从所有粒子趋近全局最优和局部最优的角度进行设计,处在同代的粒子往往采用同一惯性权重来进行位置更新,没有考虑同代粒子之间的差异性。但必须指出的是,在PSO迭代前期,数值偏大的同代权重可能会导致位置更优的粒子更新步长过大,进而降低粒子的局部寻优能力。在算法迭代中后期,数值偏小的同代权重可能会导致位置更劣的粒子更新步长过小,进而降低了粒子的全局寻优能力。另者,对于一些精度要求高的多峰值寻优问题,在算法迭代后期,粒子惯性权重减小过快将会严重影响PSO收敛精度。针对以上问题,本文提出一种多尺度简化粒子群优化算法(Multiscale Simplified Particle Swarm Optimization,MSPSO)。该算法根据每个粒子位置的优劣划分不同尺度的惯性权重,充分发挥粒子全局寻优和局部寻优能力。
当粒子适应度值fvi(k)较大,粒子越趋近于当代最优粒子时,则该粒子在下一次更新应采用小尺度的惯性权重以增强粒子的局部搜索能力。小尺度惯性权重为:
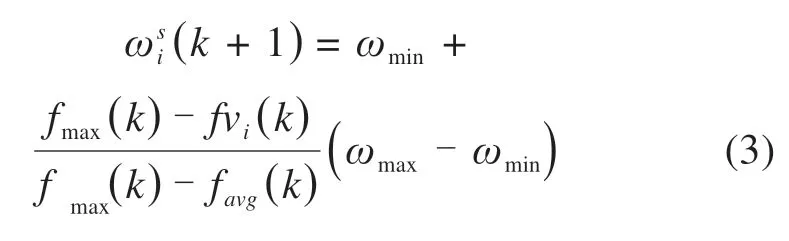
式中:ωsi(k+1)为第k+1代种群中第i个粒子的小尺度惯性权重;ωmax为最大惯性权重,通常取0. 9;ωmin为最小惯性权重,通常取0.4[16];fvi(k)为第k代种群中第i个粒子的适应度值;fmax(k)为第k代种群中最大的适应度值;favg(k)为第k代种群适应度值的平均值。
反之,当fvi(k)较小,粒子越趋近于当代最劣粒子时,则该粒子在下一次更新应采用大尺度的惯性权重,以增强粒子的全局搜索能力。大尺度惯性权重为:
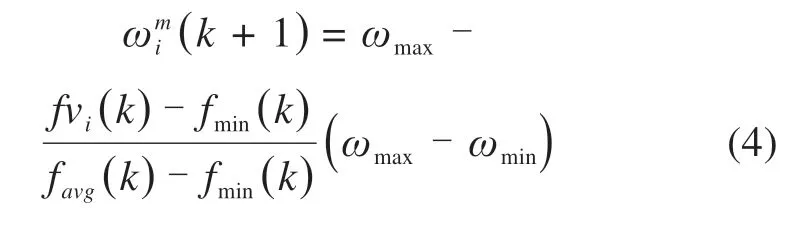
多尺度惯性权重设置为:

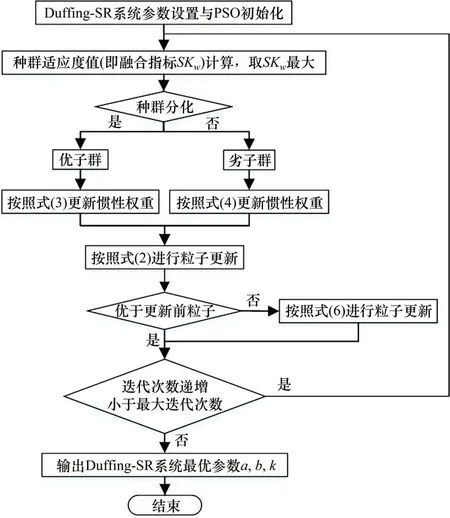
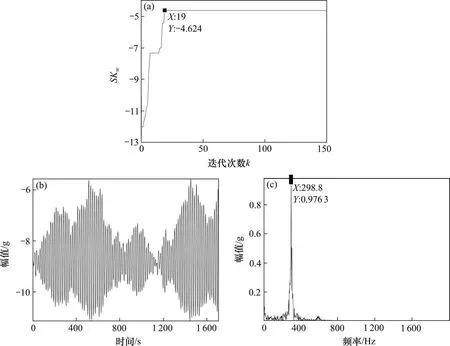
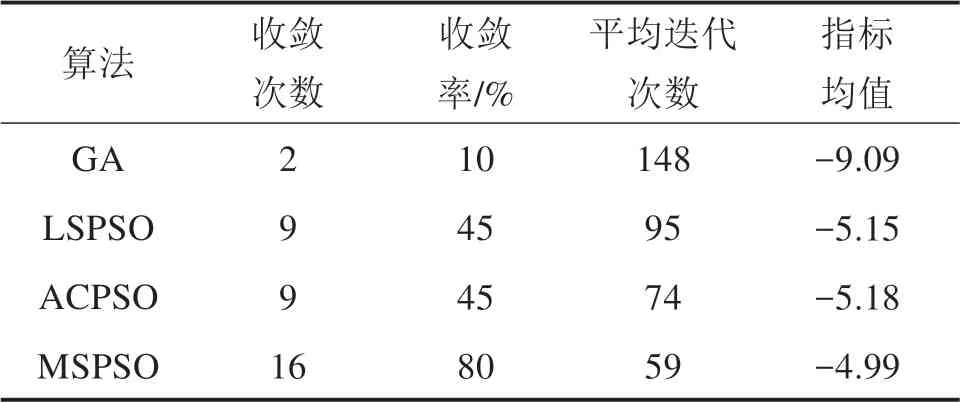
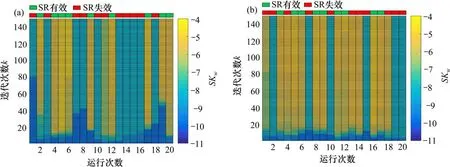
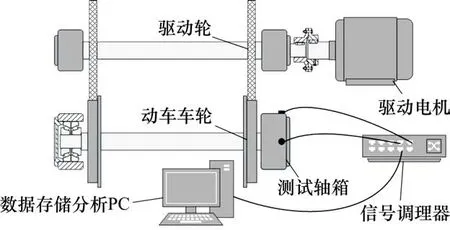
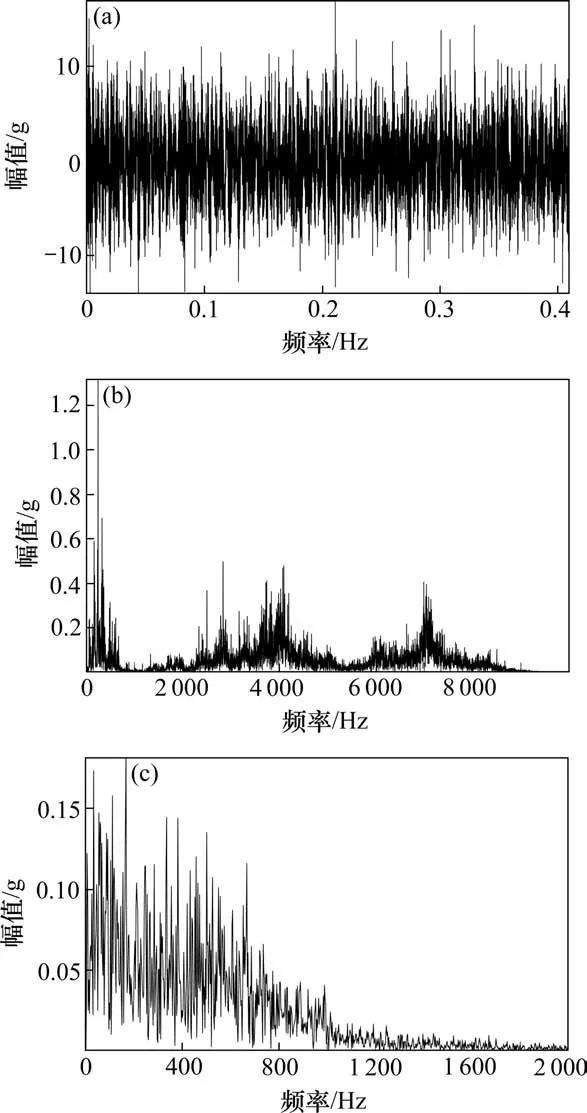
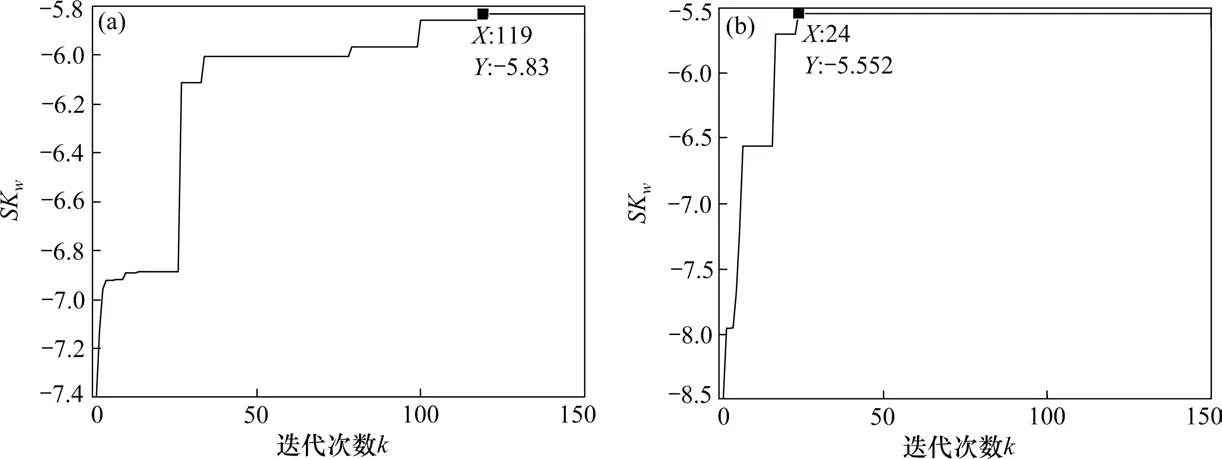
多尺度惯性权重的基本思想为:粒子在寻优过程中,自动以favg(k)为基准,将粒子种群分为优劣2个子群。对于优子群,即fvi(k)≥favg(k),fmax(k)-fvi(k)越小,代表该粒子越趋近于当代最优粒子,则该粒子在下一次更新应采用小尺度的惯性权重,这时该粒子的局部搜索能力增强,算法寻优精度高。对于劣子群,即fvi(k) 对于多维粒子的同步更新,很难保证每个维度的粒子元素都朝着目标函数的更优方向更新,有可能出现某维度粒子劣化的现象,因此有必要对每个维度的粒子搜索方向进行限制,使各维度粒子都朝着目标函数更优方向搜索。首先根据式(2)得到更新后的粒子Xi(k+1),同时比较更新前后粒子目标值的大小,若更新后目标值优于更新前目标值,则保留该维元素更新,反之,采用式(6)进行粒子第j维元素的更新。 式中:c0为学习因子,通常取为 2;r0为[-1,1]之间服从均匀分布的随机数;Xmaxj与Xminj分别表示每个粒子第j维元素的最大值与最小值;Tmax为最大迭代次数。 构造一个合理的、安全性高的适应度函数不仅可以作为衡量优化得到的DSR对弱故障信号的增强效果,同时是检测改进粒子群算法收敛速度及收敛精度方面是否有所提高的判断标准。在输入、输出信号的谱线十分明确时,SNR可作为SR的衡量指标,但SNR缺乏对非周期性的冲击信号的敏感性。因此,文献[17]提出了加权峭度Kw来作为SR衡量指标,即: 式中:C1为随机共振输入与输出信号的互相关系数,取值介于(0,1)之间;sgn()为符号函数,保证随机共振输入与输出信号的相位尽量一致;K为随机共振输出信号的峭度指标;r为小于1的正实数,这里取0.46。Kw既保留指标对脉冲成分的敏感性,使得输出中有更好的冲击出现,也保证了输出信号与输入信号间一定的相似性,避免冲击漏检现象发生。 要指出的是,尽管以Kw为优化目标的SR系统可以有效提取强噪声掩盖下的微弱冲击序列,但是在检测信号存在多种强弱不同的复合脉冲,强脉冲对K值的影响较大且远大于弱脉冲对K的影响时,造成SR优化目标中只呈现出对强脉冲的增强效果,从而遮蔽了弱冲击的共振效应,造成弱脉冲SR检测失效。为了规避这种强脉冲对弱脉冲的遮蔽现象,本文在Kw基础上融合了目标信号检测频率处的信噪比,通过对目标信号的检测的约束来增强SR对弱故障冲击的敏感性,同时也提高对其他干扰强脉冲的鲁棒性,提出了如式(8)的综合指标: 式中:|X(fd)|指随机共振系统输出的功率谱中故障特征频率所对应的幅值大小;|X(fj)|表示除了特征频率外的其他频率幅值。 以式(8)中的SKw最大化为随机共振输出的目标函数,基于MSPSO优化的DSR方法实施步骤如图1所示,主要步骤如下: 图1 提出方法流程图Fig.1 Flow chart of the proposed method 1)相关参数的设置。设置种群规模N,粒子维数D,最大迭代次数Tmax,各参数寻优范围、待检故障频率fd,变尺度系数R及线性幅值变换系数ε。 2)种群位置的初始化。在设定的寻优范围内随机初始化种群的初代位置。 3)适应度值评价。将粒子位置代入式(1)的Duffing-SR系统,采用四阶龙格库塔算法求解系统输出,并根据式(8)计算适应度函数值,根据SKw最大化原则更新个体历史最优解和群体历史最优解。 4)种群的分化及惯性权重的自适应调整。同代种群根据当代种群适应度值的平均值来实现优劣子群的分化,根据式(3)~(4)进行惯性权重的自适应调整。 5)种群位置的更新。根据式(2)与式(6)更新种群位置。 6)终止。重复步骤(3)~(5),当迭代次数超过设定值Tmax时,循环终止,此时系统SKw最大值所对应的系统参数a,b,k即为当前最优参数。 通过多对轴承滚动体故障仿真信号分析基于MSPSO的DSR方法有效性。滚动轴承元件发生单点局部损伤时传感器拾取到的振动信号的数学模型表达式为: 式中:A,B为大于0的常数;f1为调制频率;α为冲击信号衰减指数;T为故障特征周期,即1/T为故障特征频率;f2为轴承系统某阶固有频率;U(t)为单位阶跃函数;n(t)为噪声。取模型参数集[A,B,α,T,f1,f2]分别为[2,1.5,300,1/300,0,3000]与[2,0.4,300,1/120,20,3 000]时的仿真信号,模拟滚动轴承外圈故障与滚动体故障。将2个仿真信号叠加后,加入信噪比为-14 dB的高斯白噪声后,得到轴承复合故障仿真信号,如图2所示,采样频率为12 000 Hz,采样点数4 096。 图2 故障仿真信号Fig.2 Fault simulation signal 采用分层次检测方法,首先对外圈故障仿真频率300 Hz进行检测,令SKw中fd=300 Hz,设置DSR系统中R=5 000和ε=0.01可将原始信号变换成满足小参数条件限制的低频小幅值信号,设置MSPSO的种群大小为30,最大迭代次数为150,粒子维数为3,寻优范围均为[0.001,5],粒子的维数即对应DSR系统中需要优化的3个参数a,b,k,采用本文提出的MSPSO算法对DSR系统参数进行优化。图3(a)给出了MSPSO寻优收敛曲线,经过19次迭代后得到的DSR系统最优参数为a=7.82×10-2,b=1×10-3,k=1×10-3,对应的系统输出的结果如图3(b)~3(c)所示。通过参数优化后的DSR系统达到阱内随机共振状态,将噪声能量成功转移到外圈故障频率处,从而有效地检测出轴承外圈早期故障频率,故障频率处的幅值经过SR处理之后增大了约10倍。 图3 Duffing-SR系统对外圈仿真故障的检测结果Fig.3 Duffing-SR system’s detection result of outer ring simulation failure 针对滚动体故障,调整SKw中fd=120 Hz,其他系统参数不变,采用本文提出的MSPSO算法对DSR系统参数进行优化,得到如图4(a)的粒子寻优收敛曲线,经过49次迭代后参数寻优结果为a=1×10-3,b=1×10-3,k=1.13×10-3,对 应 的DSR系统输出结果如图4(b)~4(c)所示,DSR系统达到阱间随机共振状态,输出的滚动体故障频率处幅值增大了约139倍。 图4 Duffing-SR系统对滚动体仿真故障的检测结果Fig.4 Duffing-SR system’s detection results of rolling element simulation failure 为了进一步分析MSPSO优化后DSR系统的稳定性,图5(a)和(b)分别给出了进行120 Hz频率检测时MSPSO算法的寻优迭代带状图及色谱图。从图5(a)带状图可见,每次运行的SKw指标上升速度都较快,说明每次运行MSPSO都能较快收敛。从图5(b)色谱图中的灰色深度变化情况可知,除了第3,5,11和18次运行收敛后的SKw取值较小外,其他16次运行结果得到的评价指数都较高,且这16次均实现了DSR对120 Hz故障频率的准确检测,可见MSPSO算法具有较好的稳定性。图6(a)与6(b)提供了线性惯性权重SPSO(LSPSO)与自适应混沌惯性权重SPSO(ACPSO)[18]对DSR系统参数寻优的收敛色谱图。从图6(a)可见大面积的深色灰度区域,说明每次LSPSO寻优收敛后的评价指数都不理想,DSR失效次数多。这主要是因为,LSPSO采用线性递减权重,随着迭代次数的增加动态权重由最大线性递减至最小,不能很好地跟踪适应度值的变化。图6(b)ACPSO粒子优化的收敛次数比图6(a)明显增多,但是出现了多次粒子优化收敛但DSR失效的情况。这是因为,尽管ACPSO算法在粒子寻优初期使用较大的惯性权重,后期采用较小权重来兼顾粒子局部与全局的搜索能力,但并没有对粒子寻优过程中的实际位置的优劣性进行判别,不能达到寻优位置与方向的实时调节,易出现早熟收敛现象。表1给出了遗传算法和3个粒子群算法20次寻优结果的统计指标,其中遗传算法的染色体数量和进化次数与粒子群算法的种群大小和迭代次数保持一致,染色体编码长度、交叉概率、变异概率参照文献[11]设定,由表中数据可见粒子群算法的寻优效果明显优于遗传算法,且MSPSO算法的有效性、收敛速度、寻优精度都显著高于另外2种粒子群算法。本文提出的MSPSO能保证在同一代的不同粒子拥有不同的惯性权重,进而使种群拥有不同尺度的搜索能力,多尺度惯性权重随着种群进化拥有更强的跟踪能力,从而使得优化后的DSR系统能有效对微弱信号进行共振增强检测。 表1 4个算法的性能比较Table 1 Performance comparison of the four algorithms 图5 MSPSO算法20次寻优迭代Fig.5 20 optimization iterations of MSPSO algorithm 图6 LSPSO与ACPSO算法20次寻优迭代Fig.6 20 optimization iterations of LSPSO and ACPSO algorithms 以某型号动车组轴箱轴承为研究对象进行分析,试验过程在整车滚动综合性能试验台上完成,列车前后有用来固定整节车厢的反力装置,列车侧面的装置可提供横向作用力用来模拟列车运行过程中的侧向风力,图7为试验台结构示意图,试验轴箱轴承类型为双列圆锥滚子轴承CRI-2692,节圆直径为183.929 mm,滚动体直径为26 mm,滚动体个数为19个,接触角为10°。2个加速度传感器分别布置在轴箱竖直方向和水平方向的位置,使用NI InsightCM系统进行数据采集和文件管理,采样频率为20 000 Hz,试验中通过驱动轮驱动动车车轮转速至1 233 RPM,对应动车速度为200 km/h。当试验轴承存在外圈滚道锈蚀与滚动体压痕时,垂直方向传感器获得的0.4 s的试验信号如图8所示。轴的转频为20.55 Hz,通过相应计算可得外圈理论故障频率为168.04 Hz,滚动体理论故障频率为71.28 Hz。 图7 试验装置示意图Fig.7 Schematic diagram of test device 从图8(a)~8(b)可见,轴箱轴承复合故障的时域波形复杂,故障冲击成分完全被噪声淹没,而功率谱中频谱成分复杂,存在较多的边频信号干扰,难以进行故障辨识。在图8(c)的共振解调谱中,频率成分非常复杂,无法识别轴承故障频率。根据原始信号的理论故障频率和幅值大小可选取随机共振系统的变尺度系数为5 000,线性幅值变换系数为0.01,分层检测的故障fd依次设置为168.04 Hz与71.28 Hz。设置MSPSO算法的种群大小为30,最大迭代次数为150,粒子维数为3,a,b和k3个参数的寻优范围均为[0.001,5]。 图8 轴承故障信号Fig.8 Bearing fault signal 图9(a)~9(b)分别为对外圈故障频率和滚动体故障频率进行检测时DSR参数优化的粒子群收敛曲线图。从图9(a)可见,针对外圈故障检测的MSPSO经过119次迭代后收敛,输出的DSR最优参 数 为a=2.57×10-2,b=1×10-3,k=5.16×10-2。图9(b)中,针对滚动体故障检测的MSPSO经过24次迭代后收敛,输出的DSR最优参数为a=1.07×10-3,b=1×10-3,k=1×10-3。 图9 收敛曲线Fig.9 Convergence curve 采用优化后的DSR系统得到外圈故障与滚动体故障的检测结果分别如图10(a)~10(b)与图11(a)~11(b)所示。在图10(a)中的时域波形在负半轴分布,说明系统发生阱内共振。图10(b)中的频谱图显示,在外圈故障特征频率166 Hz处有明显的冲击,且周围十分光滑,没有较多的其他干扰成分,验证了测试轴承中外圈故障的存在。图10(c)~10(d)给出了采用LSPSO与ACPSO优化方法得到的DSR系统对外圈故障的检测输出,前者出现了虚假故障频率的共振输出,后者则未实现系统的有效共振,造成了故障检测的失败。同理,在图11中,采用本文提出的MSPSO优化的DSR,系统输出故障频率为70.8 Hz,与滚动体的理论故障频率仅相差0.48 Hz,而采用其他2种优化算法检测出的频率分别为75.68 Hz与90.33 Hz,都与滚动体理论故障频率相差甚远,属于虚假故障频率。图10与图11的分析结果,充分验证了本文提出的基于MSPSO的DSR系统对高铁轴箱轴承复合故障诊断的有效性与优越性。 图10 外圈故障的DSR检测输出Fig.10 DSR detection output of outer ring fault 图11 滚动体故障的DSR检测输出Fig.11 DSR detection output of rolling element failure 1)提出了一种多尺度简化粒子群优化算法,采用多尺度惯性权重对粒子位置进行更新迭代,考虑同代粒子之间的差异性,充分发挥了粒子局部寻优能力与全局寻优能力。该优化算法对每个维度的粒子搜索方向进行了限制,使各维度粒子都朝着目标函数更优方向搜索,从而提高了寻优速度与效果。 2)采用MSPSO对DSR系统进行了结构参数优化,并引入了信噪比融合加权峭度的评价指标为DSR的适应度函数。该融合指标充分考虑了随机共振信号对故障脉冲的敏感性,也规避了对弱冲击漏检测问题,通过目标信号检测频率处的信噪比约束,增强了DSR对信号奇异点的鲁棒性。 3)采用MSPSO优化后的DSR系统对仿真信号进行了分析,并应用在高铁轴箱轴承故障诊断中。试验结果表明,提出的方法能够有效地检测出轴箱轴承复合故障,对弱故障冲击有更好的增强效果,具有较好的工程应用前景。
3 优化随机共振系统
3.1 复合适应度函数构造
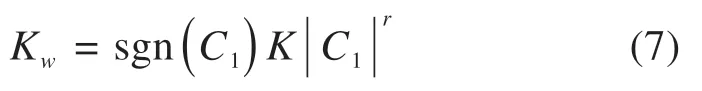
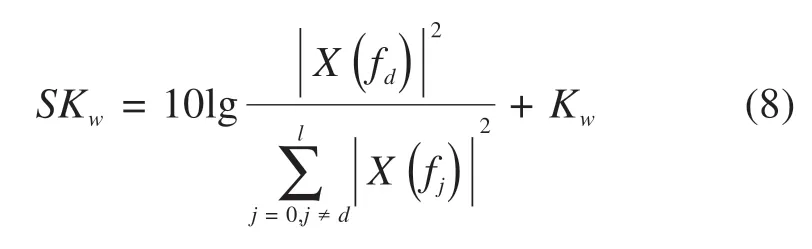
3.2 方法实施步骤
4 仿真分析
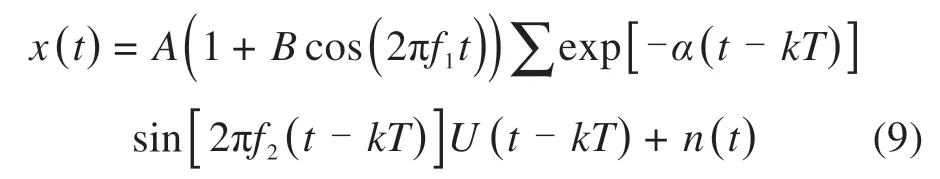



5 在高铁轴承故障诊断中的应用


6 结论

