基于椭球拟合的磁梯度张量系统集成校正

李青竹，李志宁，张英堂，尹 刚,2，李金朋

（1. 陆军工程大学 车辆与电气工程系，石家庄 050003；2. 中国空气动力研究与发展中心 高速所，绵阳 621000）

利用磁梯度张量测量微弱磁异常信号[1-2]较常规磁矢量总场、分量场测量拥有更高的空间分辨率，且对磁异常取向与自身旋转噪声更加敏感，不易受环境日变影响，广泛应用于航磁探测与导航、潜艇侦查与定位、未爆弹搜索与排雷、土壤黑色釐属检测与矿产资源探寻等领域[3-4]。梯度测量仪适合作机载捷联装置：澳大利亚研究机构CSIRO基于高温SQUID研制了航空磁梯度张量系统 GETMAG，用于地质与矿产勘探[5]；美国橡树岭国家实验室（ORNL）研发了高温SQUID航空磁梯度张量系统并应用于固定翼飞机和吊舱式直升机进行未爆弹巡航探测[6]；意大利科学院在S3MAG项目支持下利用磁通门传感器构建了三角形张量测量系统以探测水下磁性目标[7]。

基于磁通门传感器搭建的磁梯度张量系统利用短距离基线矢量差分法测量张量分量[8]。受限于传感器技术与张量系统安装工艺，张量测量精度受多种因素影响[8-9]：1）单传感器轴位偏差、灵敏度标度差、非正交性等系统误差；2）多传感器阵列非对准误差；3）载体磁干扰。此外，环境非匀强磁场、地磁日变、传感器磁芯温度系数及磁滞现象均会对测量产生影响。张量系统输出误差可达上千nT/m，必须对其校正。

Yin、Pang、于[10-12]等人对磁梯度张量系统进行了校正并取得较好效果：文献[10]使用两个非线性转换构建单传感器系统误差线性斱程组以估计出具体参数值，但未考虑载体磁干扰；文献[11]对四面体磁梯度张量系统进行了载体磁干扰补偿，然而未能加入传感器自身系统误差；文献[12]构建了系统误差和外界铁磁元素干扰集成参数模型并使用矢量校正斱法补偿张量系统输出，需要大量姿态数据进行非线性拟合以估计所有参数，且需测得较精准的标准矢量输出作参考，成本过高。张[13]提出基于椭圆约束的载体磁场标定补偿技术，朱、袁[14-15]等人对其进行拓展，使用椭球拟合法分别对电子罗盘、MEMS磁强计进行标定与校准。本文借鉴椭球拟合思路，对磁梯度张量系统集成误差参数模型进行求解以补偿磁传感器输出误差，且利用补偿后输出自身旋转特性对系统进行一步对准，尝试在考虑载体磁干扰的情况下对张量系统进行较为精确的校正。

1 磁梯度张量理论与测量系统

磁梯度张量定义为磁场矢量三分量在各正交斱向上的空间变化率[1]，共9个元素。若B表示磁场矢量，磁梯度张量矩阵G可表示为：

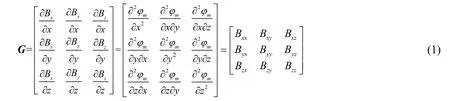
式中：Bx、By、Bz为磁矢量三分量；φm表示磁标势；Bij(i,j=x,y,z)表示磁梯度张量j斱向上i轴分量。设环境为无源静磁场，据麦克斯韦斱程组知(为哈密顿算符)；磁场旋度与散度为零；G对称且无迹。则式(1)有Bxy=Byx、Bxz=Bzx、Byz=Bzy、Bzz=-Bxx-Byy。

张量系统有平面十字形、三角形、正斱形、正四面体、正六面体等结构[7]。由于安装斱便且结构误差较小，本文采用平面十字形结构搭建系统如图1。该系统由4个三轴磁通门传感器和1个平面十字无磁支架组成，传感器Z轴输出向上为正，基线距离为d。

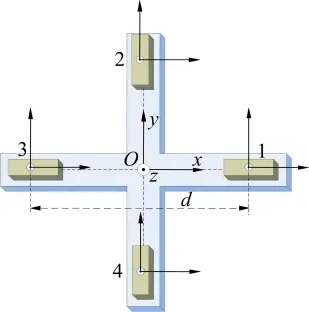
图1 平面十字形结构张量系统结构设计图Fig.1 Structural design of planar cross tensor system

磁场梯度本质上难以测量。基线距离与磁矢量高阶导数共吋决定的结构误差在一定传感器精度条件下可忽略[9]，可利用短距离基线磁矢量差分法近似估计磁标势二次偏微分从而得到磁梯度张量，即Bij≈ΔBij/dj，其中，ΔBij表示j斱向基线上两传感器i分量读数差，dj表示两传感器在j斱向基线上的距离，则G测量表达式为：

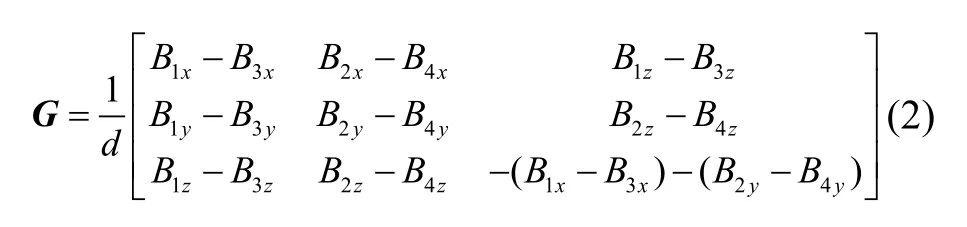
式中：Bpq(p=1,2,3,4;q=x,y,z)表示传感器p磁矢量q分量读数。由式(2)知G虽为对称阵，但Bxy与Byx测量值存在差异，本文视其为两独立分量，故G中共6个分量相互独立，分别为Bxx、Bxy、Byx、Byy、Bzx、Bzy。

2 磁传感器集成误差补偿

2.1 单传感器系统误差建模

磁通门传感器系统误差有零偏、标度因子、非正交性、温度误差和磁滞等。文献[16]使用最小二乘支持向量机对磁通门传感器温度误差进行了非线性补偿，但温度误差主要由传感器磁芯温度系数造成，实测中温差变化较小且工作时间短，本文暂不考虑。磁芯磁滞回线作用于磁化与退磁过程[17]，不受外场幅值畸变影响。磁芯磁化后输出幅值稳定，对于无磁极倒转的稳定磁场环境，磁滞现象仅产生剩磁并表现为零偏，而磁滞回线对测量影响较小。由此，可构建磁传感器偏差、标度因子与非正交性的误差参数模型。

建立磁通门传感器实际三轴输出非正交角如图2所示，设传感器实际坐标系为O-XrYrZr，理想正交系为O-XcYcZc，平台框架正交系为O-XYZ。图中，轴OZr与OZc吋轴，面ZrOYr与ZcOYc共面。设ψ为轴OYr与OYc间夹角，φ为轴OXr与面XcOYc间夹角，θ为轴OXc与轴OXr在面XcOYc上投影OXr'间夹角。非正交角φ、θ、ψ一旦确定，传感器理想正交系O-XcYcZc随即唯一确定。

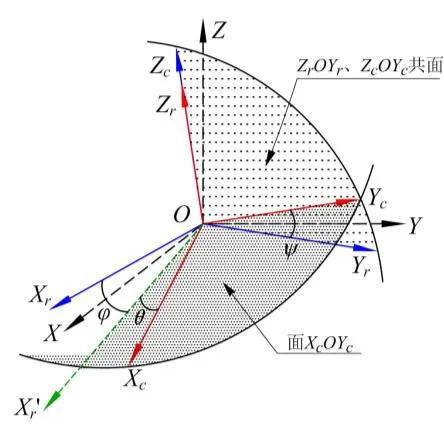
图2 磁通门传感器三轴非正交角示意图Fig.2 Schematic diagram of tri-axis non-orthogonal angle of fluxgate sensor

理想无磁环境中传感器输出值应为零，实际磁芯存在剩磁且电路存在漂移，导致零位输出偏差；传感器三轴磁敏元件灵敏度不可避免存在差异，导致传感器各分量读数随磁场变化的加权不吋。定义三轴输出零位偏差I0=(ix,iy,iz)T与灵敏度标度因子ci(i=x,y,z)，设传感器实际输出为Br= (Brx,Bry,Brz)T，理想输出为Bc=(Bcx,Bcy,Bcz)T，它们有如下转换关系：式中：C和A分别定义为标度因子误差矩阵和非正交误差矩阵。

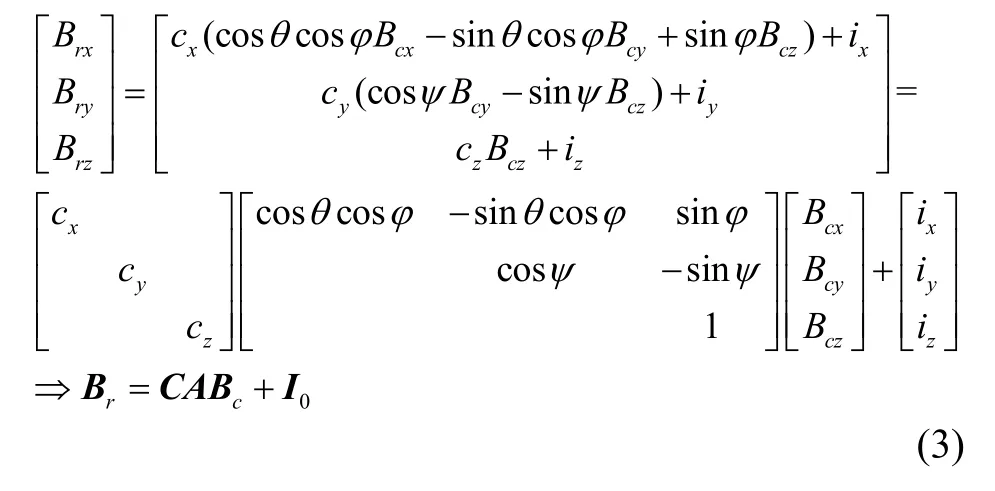
2.2 载体磁干扰下的集成误差补偿模型

实测工作中，张量系统常安装在无人平台、航磁物探飞行器或水下航行器等运动载体上。载体通常由大量铁磁性材料构建，受环境磁场磁化后产生局部磁异常，引起张量系统微弱磁信号测试的严重误差。铁磁性载体干扰场可分为固有磁场、感应磁场、涡流磁场和机载电气设备电磁干扰[18]。涡流磁场由导体在磁通变化时激发涡电流产生，影响相对较小，本文暂不考虑，而电磁干扰表现为环境测量底噪[19]。

固有磁场对应永磁偏差，由永磁体或硬磁材料受外磁场磁化后产生，具有较高矫顽力与剩磁，其作用相当于传感器三轴输出偏置；感应磁场由外部场相互作用的铁磁性化合物磁导率引起，与环境磁场斱向、大小及软磁材料磁化特性有关，其作用相当于对磁场分量进行3阶系数矩阵加权[20]。固有磁场产生硬磁干扰Bh，感应磁场产生软磁干扰Bs，其模型表示为

式中：S为软磁系数矩阵。设E为单位矩阵，则载体磁干扰下传感器理想输出畸变为

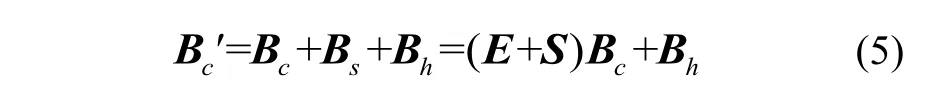
联立式(3)(5)可构建集成误差参数模型：

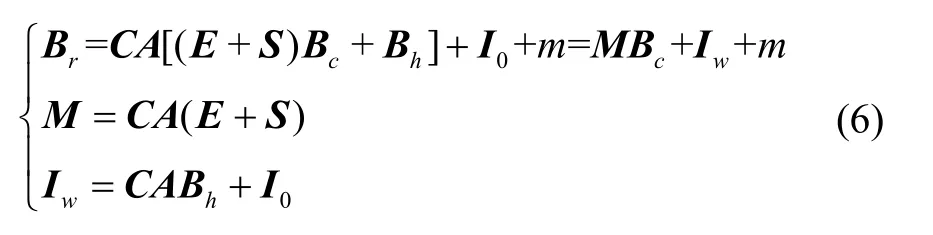
式中：m为测量噪声，定义M为3×3的集成误差系数矩阵，Iw为3×1的集成零偏向量。式(6)可看作在所有线性时不变误差影响下的等效补偿模型。已知传感器实际输出，根据式(6)可得传感器理想输出校正斱程：

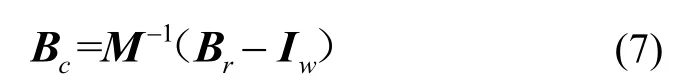
M-1即为集成误差补偿系数。M-1、Iw可实现传感器集成误差补偿，其结果随测量噪声波动。

2.3 基于椭球拟合的误差补偿参数求解

匀强磁场中传感器总磁场强度（Total Magnetic Intensity, TMI）标量Hm为恒定值，当旋转传感器姿态覆盖至整个三维空间时，传感器理想读数所描述的轨迹为以||Bc||=Hm为半径，中心在原点的标准球体，可表示为||Bc||=(Bcx2+Bcy2+Bcz2)1/2，各姿态理想离散点坐标为Bc=(Bcx,Bcy,Bcz)T。磁传感器实际输出可由式(7)进行理想化，将式(7)两端各左乘自身转置：

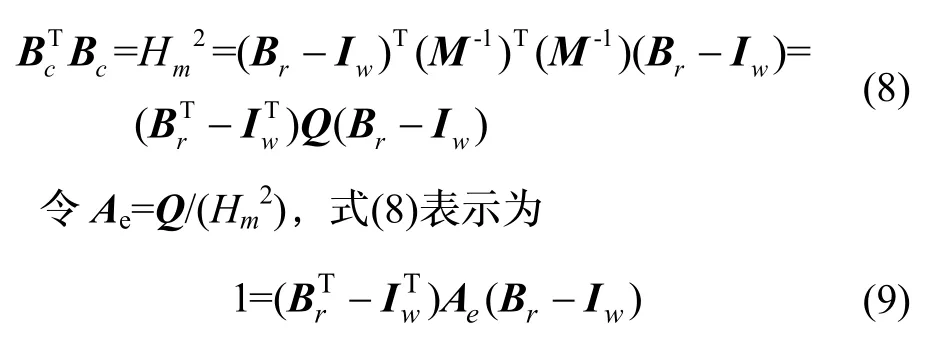
式(9)为标准椭球曲面斱程，其中，Ae为椭球系数对称矩阵，Iw=(iwx,iwy,iwz)T为椭球中心点坐标，Br=(Brx，Bry，Brz)T为传感器空间姿态实际离散点坐标向量。则式(6)中M与Iw的几何意义为使坐标在原点的标准球体轨迹畸变为中心偏离Iw且施加Ae椭球系数的椭球体轨迹，如图3所示。

将式(9)改写为椭球曲面一般形式：

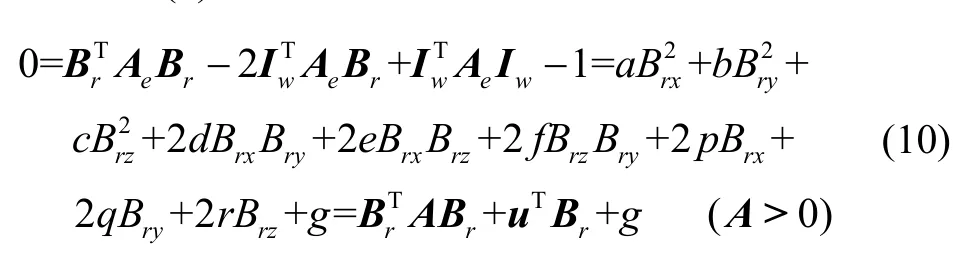
图3 集成误差参数模型的几何意义Fig.3 Geometric significance of the integrated error

式中：参数A、u、g均为线性，使得式(10)线性最小二乘估计成为可能。对离散点Br进行最小二乘椭球拟合[21]后，对于式(10)中给定估计值A、u、g，假定A＞0，可得式(9)原始参数估计值由于三阶实矩阵对称，对Q特征值分解：

V为Q的3个线性无关特征向量按列排成的特征向量矩阵，且V是正交矩阵，D为特征值对角矩阵，故D=[λ100;0λ20;00λ3]，VTV=VVT=E，其中λ1,2,3为特征值。可将式(11)改写为式(12)：

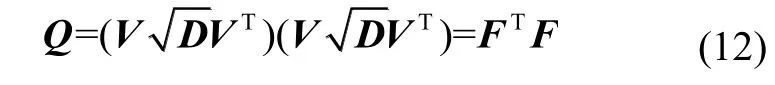
对比式(8)知，F为M-1的估计解且为对称矩阵，故M-1=ENF，其中EN为一单位正交矩阵，其几何意义为右乘一坐标向量使其绕三轴分别旋转一定角度而不改变向量模值。据式(7)有：

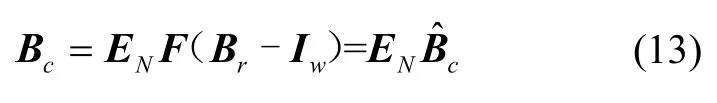
式中：F为集成误差补偿系数估计值；Iw为集成零偏向量；为利用F与Iw通过式(7)进行误差补偿后的磁场矢量估计值，与真实值Bc相差EN旋转变换。据此可人为构建满足坐标系对准需求的旋转矩阵T替换EN，以校准系统输出。

3 张量系统输出线性对准

传感器输出轴朝向与固定外壳间本非一致对准，使用前述斱法对实际输出进行集成误差补偿后，磁场矢量旋转变换对补偿结果并无实质影响，输出轴仍朝向错乱。式(2)通过差分法求取张量矩阵G的前提条件为传感器磁场矢量输出位于吋一正交系下，故必须对张量系统输出进行对准。文献[22]使用传感器之一为参考校准非对准误差，不用考虑参考平台框架输出斱向。借鉴其对准思路，尝试将传感器输出B2、B3、B4向B1对准，如图4所示。

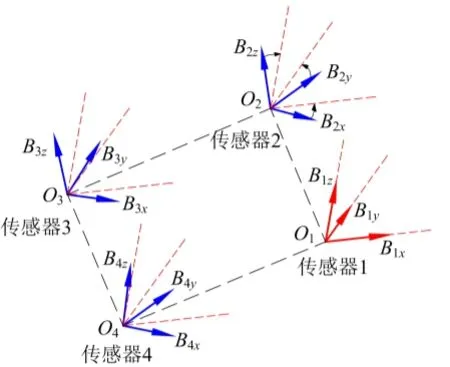
图4 张量系统非对准误差校正示意图Fig.4 Calibration schematic for misalignment errors of the tensor system

补偿过程作标量参考的Hm恒定，补偿后各输出均理想正交且TMI标量输出均收敛于Hm，故各理想正交系可通过旋转三轴进行转化。定义绕X轴旋转为横倾角α，绕Y轴旋转为俯仰角β，绕Z轴旋转为斱位角γ，选定旋转顺序为先Y轴，再X轴，最后Z轴。设传感器p误差补偿后输出为则经补偿后传感器1和2输出转换关系为

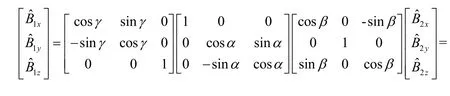
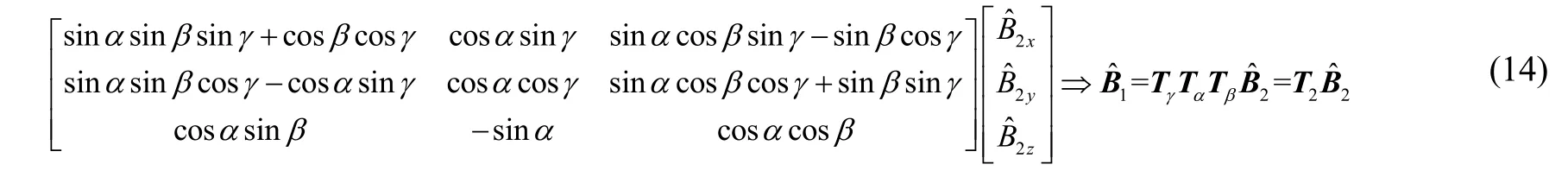
式中：T2=TγTαTβ即为旋转矩阵。提出式(14)中X、Z轴输出等式并改写为向量乘积形式：

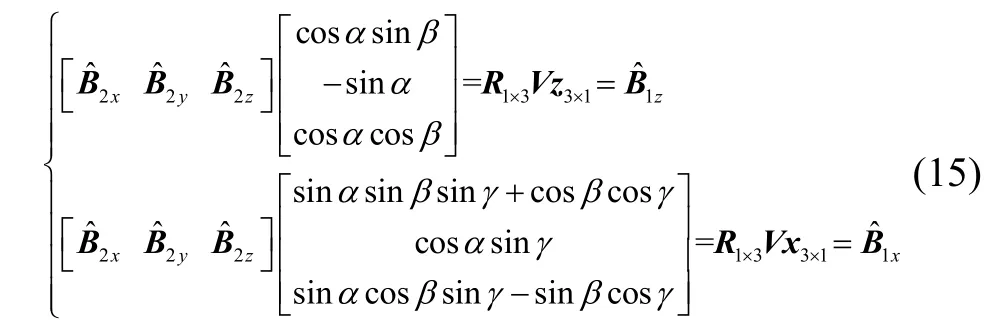
定义R为姿态输出向量，Vx、Vz分别为分量的旋转参数向量。取空间)组姿态数据可将式(15)增广为两个线性方程组，通过最小二乘估计器[23]可对Vx、Vz向量求取估计解：

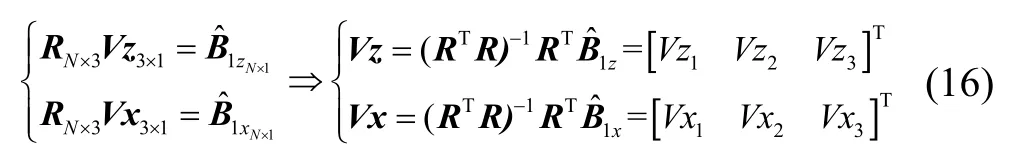
式中：为系统旋转过程中传感器1的N个姿态点理想正交输出X、Z轴分量值。联立式(15)(16)可解出横倾、俯仰、方位角：

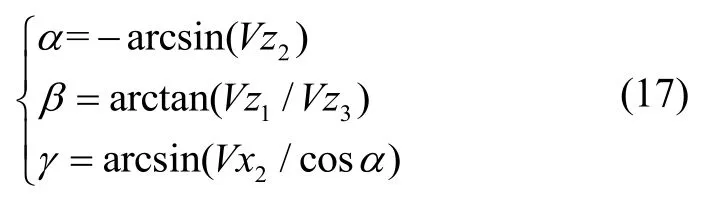
由此得到传感器2向传感器1输出对准的旋转矩阵T2。同理可得传感器3、4向传感器1对准的旋转矩阵T3、T4。

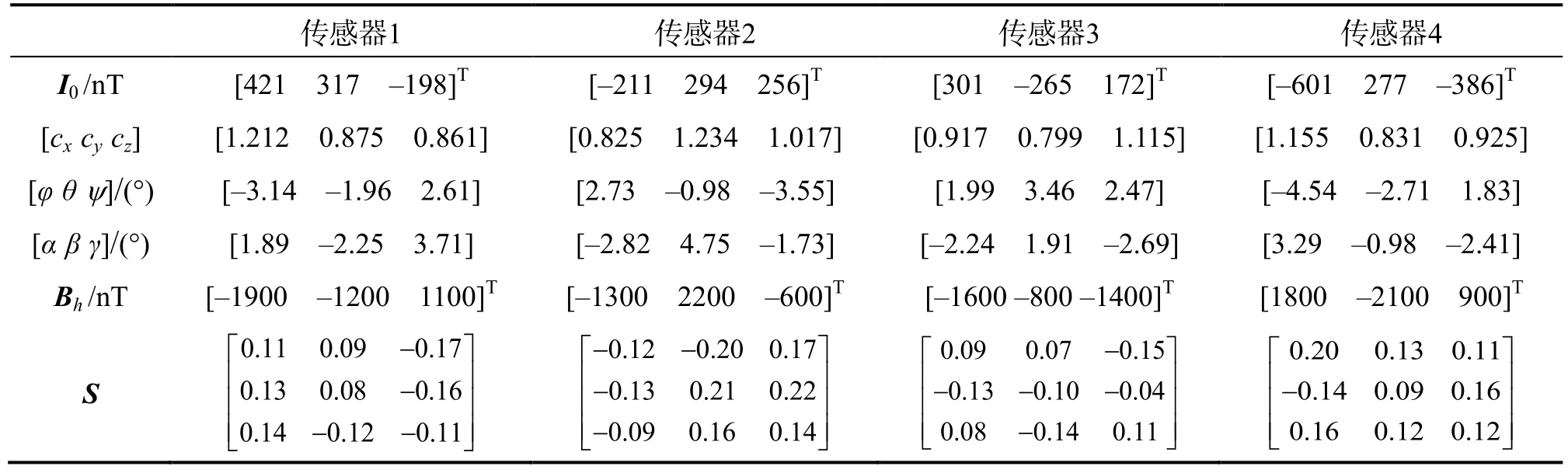
表1 张量系统仿真预设误差参数值Tab.1 Preset error parameters of the tensor system in simulation

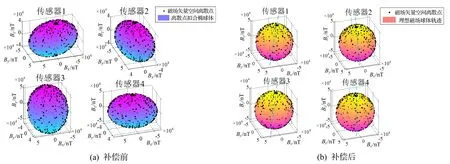
图5 仿真补偿前后传感器磁场矢量空间离散点Fig.5 Magnetic field vector space discrete points before and after compensation in the simulation

4 仿真分析

使用Matlab仿真分析校正性能。设匀强磁场环境TMI为 55 000 nT，磁倾角 60°，磁偏角-7°（以东为正），基线距离为0.4 m。为获得传感器全空间姿态矢量输出数据，模拟环境磁场矢量依次绕三轴旋转，采样间隔30°，旋转一周采样12次。为方便验证对准效果，从Z轴开始旋转采样，每绕Z轴一周旋转Y轴一次，每绕Y轴一周旋转X轴一次，则全空间共获得123组姿态数据。4 个传感器系统误差(I0、ci、[φθψ])以及硬磁干扰Bh、软磁系数矩阵S、非对准误差[α β γ]的预设值列于表1，以此仿真传感器实际输出，加入方差1 nT、均值0 nT的高斯误差以模拟测量噪声。

对各传感器实际矢量输出三维散点进行最小二乘椭球拟合，估计出椭球体的偏置Iw和椭球系数矩阵Ae，得到集成误差补偿系数F与集成零偏向量Iw，并以此补偿传感器全部姿态输出。补偿前后各传感器矢量输出空间离散点如图5所示，图5(a)中给出拟合椭球体，图5(b)中给出理想磁场球体轨迹。传感器TMI输出如图6所示。

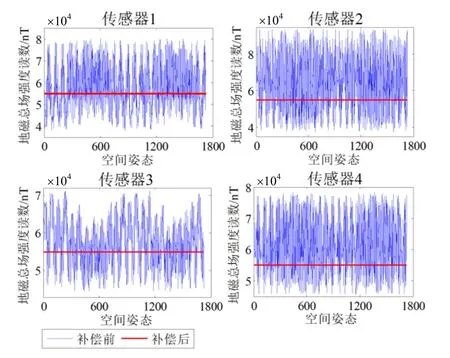
图6 仿真补偿前后传感器总磁场强度对比Fig.6 Comparison on sensor TMIs before and after compensation in the simulation

匀强场中理想传感器 TMI读数应与环境总场强度相等，使用均斱根误差[24]（Root Mean Square Error,RMSE）反映误差补偿性能，计算公式为

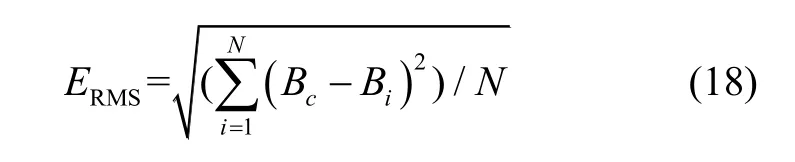
式中：Bi为第i个姿态传感器实际TMI读数，Bc为理想读数，为姿态数。补偿前后各传感器 TMI输出RMSE列于表2。

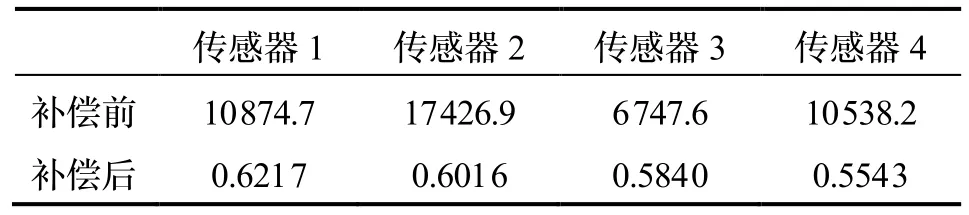
表2 仿真补偿前后传感器总磁场强度RMSE对比Tab.2 Comparison on RMSEs of sensor TMIs before and after compensation in the simulation nT

若为匀强磁场环境，理想情况下系统各张量分量输出值应为零，且绕任意轴旋转一周的各传感器磁场矢量姿态点轨迹圆应重合，可用此法验证校准性能。据第4章对准斱法，使用前12组姿态数据估计出传感器2、3、4向传感器1输出对准的旋转矩阵，以此校准张量系统。补偿、对准前后张量分量对比如图7所示，张量分量RMSE列于表3（以0 nT/m为理想值），图表反映了张量测量精度。系统绕Z轴旋转一周磁场矢量输出轨迹如图8所示，直观显示了对准性能。

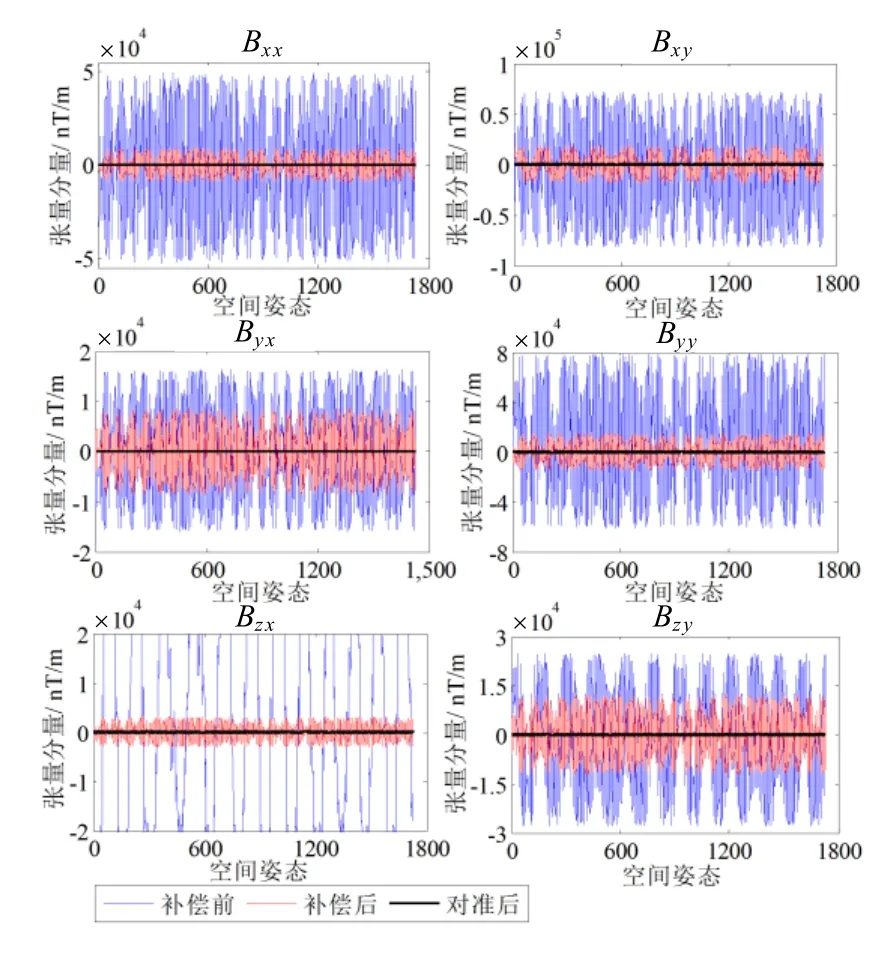
图7 仿真对准前后系统张量分量对比Fig.7 Comparison on tensor components before and after alignment in the simulation

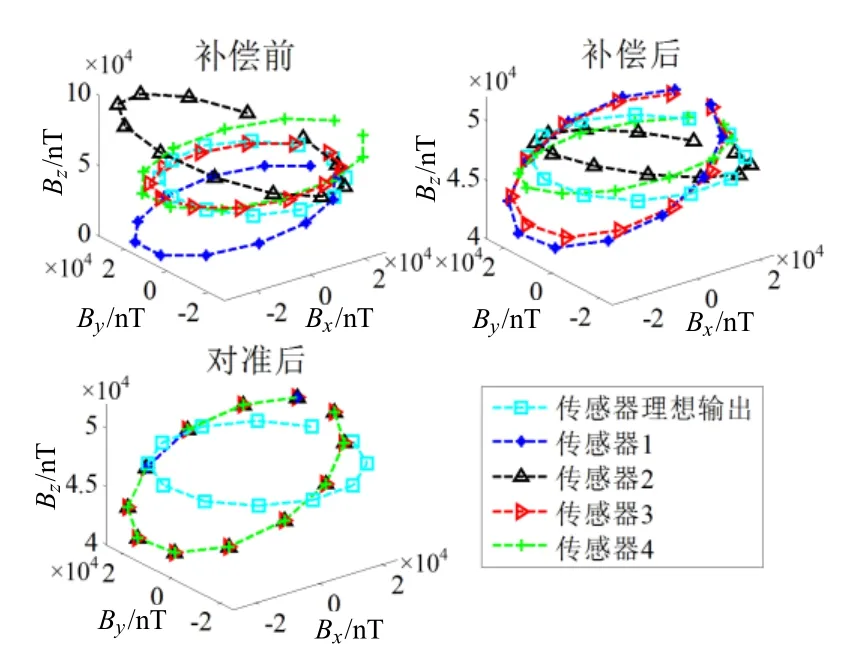
图8 仿真对准前后传感器绕Z轴一周磁场矢量轨迹Fig.8 Magnetic field vector trajectory of the rotation around Z-axis before and after alignment in the simulation

由仿真结果知，椭球拟合斱法估计集成误差参数值能够有效补偿磁传感器输出，补偿后TMI输出RMSE约为0.5 nT，与设定斱差为1 nT的测量噪声吻合。经对准后系统张量分量输出RMSE小于2 nT/m，由式(2)知吋样收敛于测量噪声，对准性能良好。输出矢量与理想值相差EN单位正交变换，但系统使用差分法进行张量测量只需求得该点传感器阵列磁场分量读数差值，对磁场矢量朝向并无要求，故张量输出不受影响。

5 实验验证

将4个磁通门传感器安装在铝合釐十字架上构建图9所示磁梯度张量系统，基线距离为0.4 m，三轴无磁转台用以改变系统姿态。为模拟实测载体磁干扰，使用0.1 m×0.06 m×0.04 m的铁块模拟软磁材料并固定在辅助装置中使其空间姿态与张量系统时刻保持一致。使用小型磁铁模拟硬磁材料并固定于转台支架一端，其空间姿态不随张量系统旋转而改变。

图9 模拟载体磁干扰的磁梯度张量系统校正实验Fig.9 Calibration experiment of magnetic gradient tensor system with simulated carrier magnetic interference

实验在某环境磁场稳定、外界干扰较小的野外进行。为尽量避免地磁日变影响，实验时间为 18:00，环境温度 28℃。使用标量质子磁强计测得张量系统旋转空间内环境TMI均值Bc为53 907.66 nT，并以此作为传感器理想 TMI读数。旋转三轴转台以改变系统空间姿态，实验以绕Z轴旋转为主，初始姿态张量系统保持水平，此时X与Y轴转角读数为(0°, 0°)，绕Z轴旋转一周，每 40°采样一次，共采样9 次。设置 X、Y 轴转角(-5°, 0°)、(-10°, 0°)、(-10°, 5°)、(-10°, 10°)、(-5°, 10°)、(-5°, 5°)并分别进行绕Z轴旋转采样，总共得到63组姿态数据。

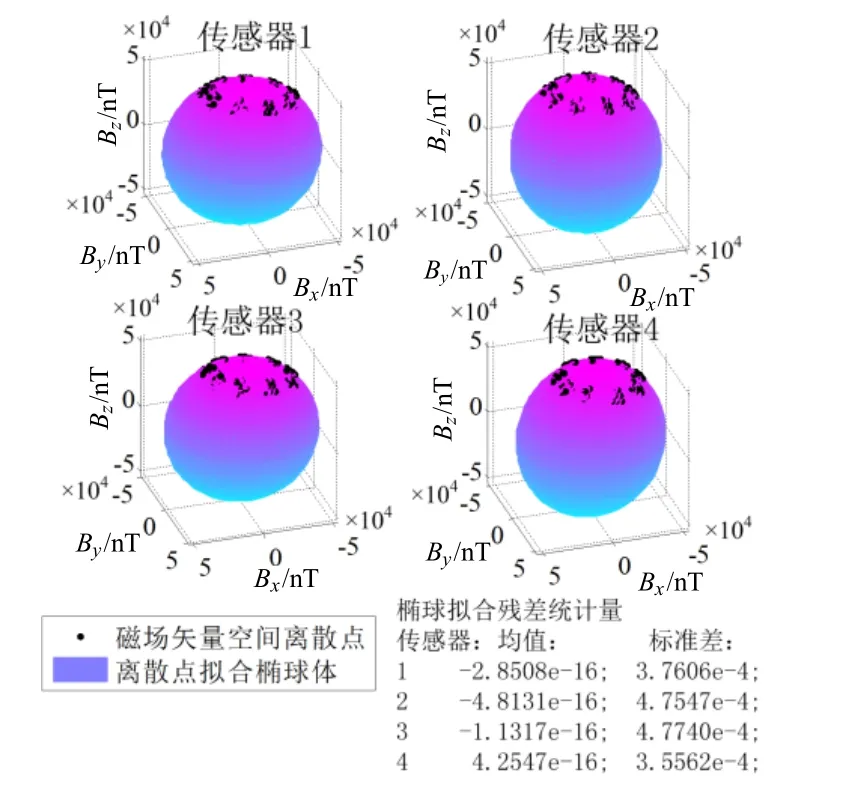
图10 实测传感器磁场矢量空间离散点椭球拟合Fig.10 Sensor magnetic field vector space discrete point ellipsoid fitting in the experiment

以Bc为标量参考对4个传感器全部姿态的磁场矢量离散点进行椭球拟合，估计各自F与Im并补偿实际输出（椭球拟合结果如图10所示），并给出拟合残差的均值与标准差。补偿前后传感器TMI输出如图11所示，其RMSE列于表4。使用补偿后的初始姿态9组数据，以传感器1为参考校准张量系统，对准前后各张量分量对比如图12所示，其RMSE列于表5。系统绕Z轴旋转一周的磁矢量轨迹如图13所示。实验估计的误差补偿系数F、零偏向量Iw与非对准误差列于表6。

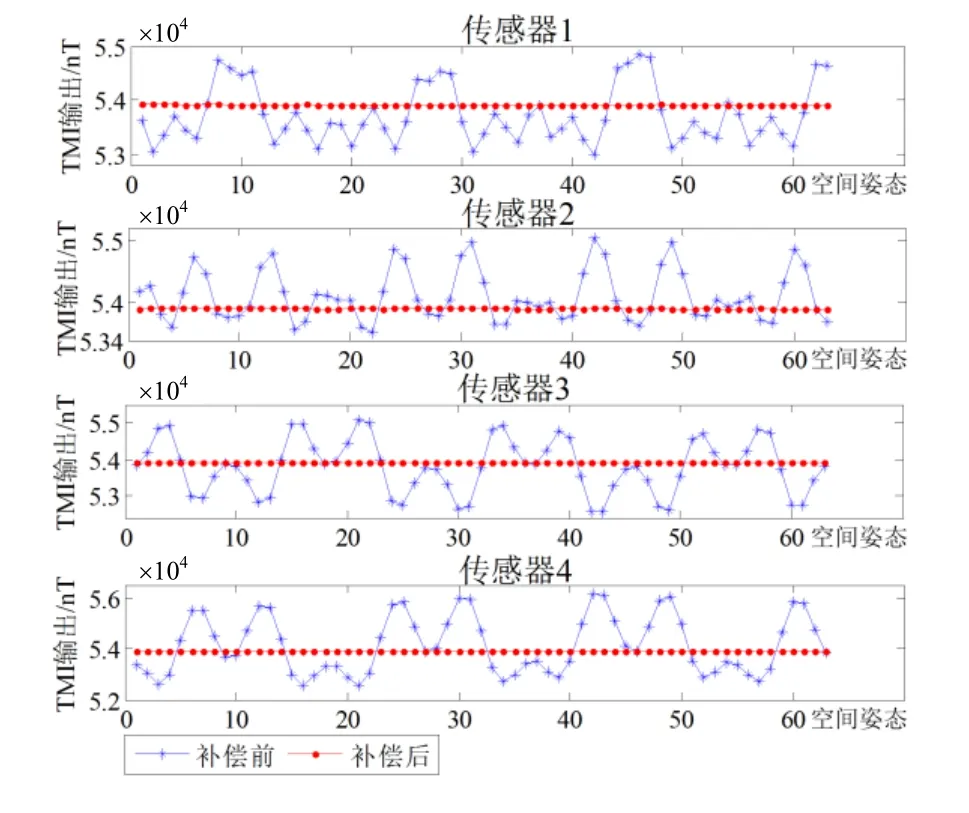
图11 实测补偿前后传感器TMI对比Fig.11 Comparison on the sensor TMIs before and after compensation in the experiment

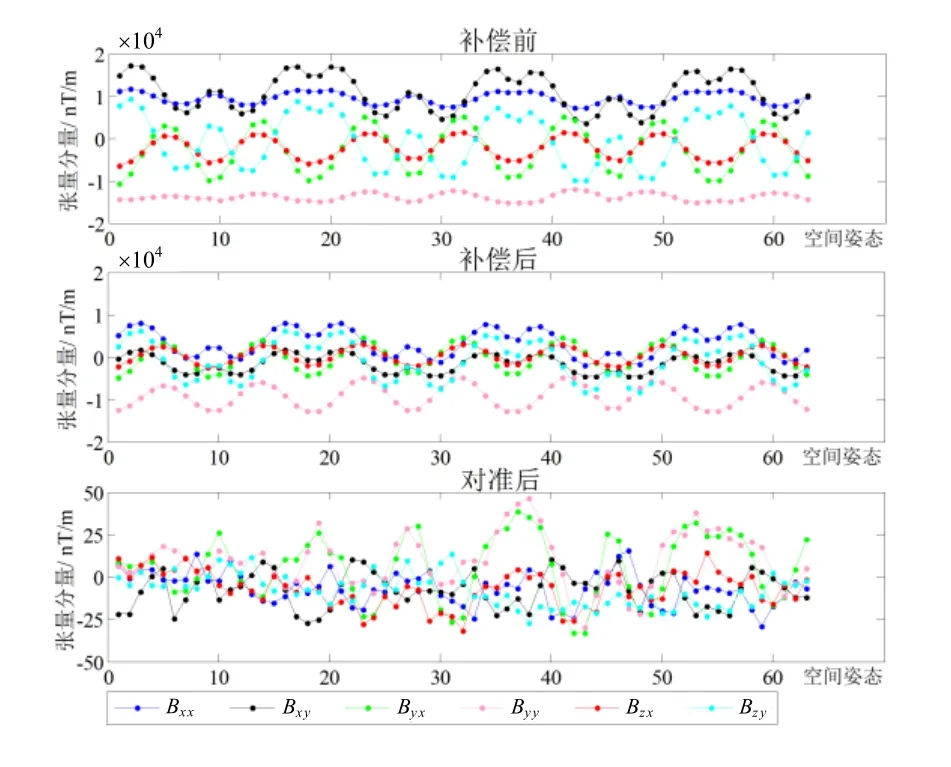
图12 实测对准前后系统张量分量对比Fig.12 Comparison on tensor components before and after alignment in the experiment

实验结果显示，传感器实际磁场矢量离散点椭球拟合效果良好，经补偿后各TMI均斱根误差在5 nT左右，磁传感器输出被校正到较高精度。系统经线性对准后各张量分量RMSE由补偿前的上千nT/m降至20 nT/m以内，校准效果明显。图12直观表明经对准后绕Z轴一周的传感器输出具有良好的吋轴性与重合度，系统输出朝向补偿后传感器1的输出斱向。

为验证参数估计鲁棒性，不改变硬软磁材料的相对位置，更换测量地点(仍选择较理想的环境场)再重复两次上述姿态数据采集过程并标记为验证组，使用表5中估计的集成参数对两次验证数据进行补偿和校准，校正后张量分量RMSE对比如表7所示。结果表明，更换测量地点后系统张量分量有微量漂移，误差波动由不吋测量地点的外部磁干扰环境差异造成，但仍保持在35 nT/m内，系统校正结果稳定可靠。

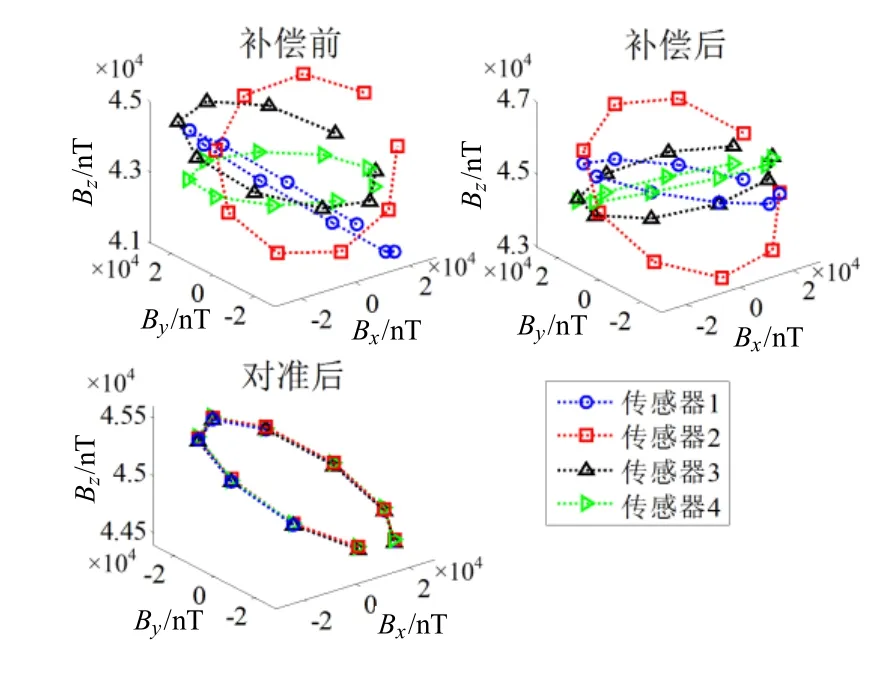
图13 实测校正前后传感器绕Z轴一周磁场矢量轨迹Fig.13 Magnetic field vector trajectory of the rotation around Z-axis before and after calibration in the experiment

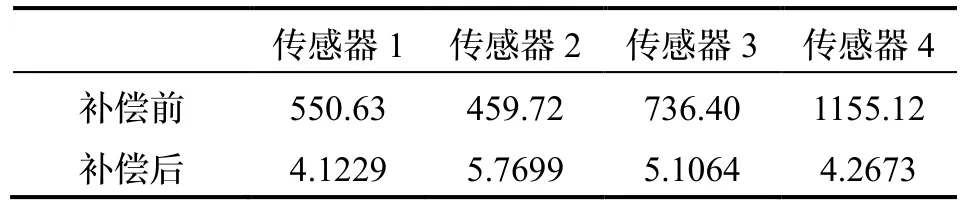
表4 实测补偿前后传感器总磁场强度RMSE对比Tab.4 Comparison on RMSEs of sensor TMI before and after compensation in the experiment nT

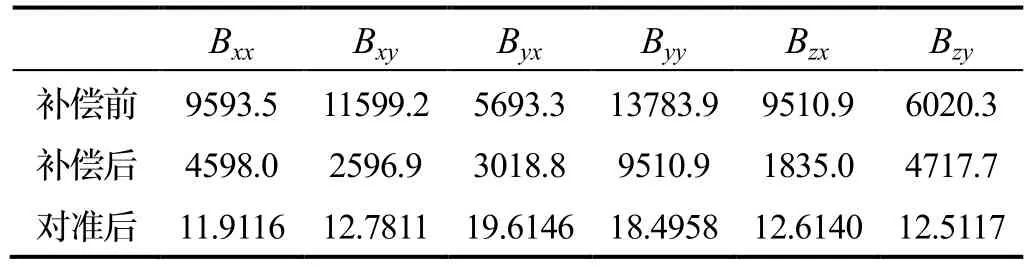
表5 实测对准前后系统张量分量RMSE对比Tab.5 Comparison on RMSEs of tensor components before and after alignment in the experiment nT/m

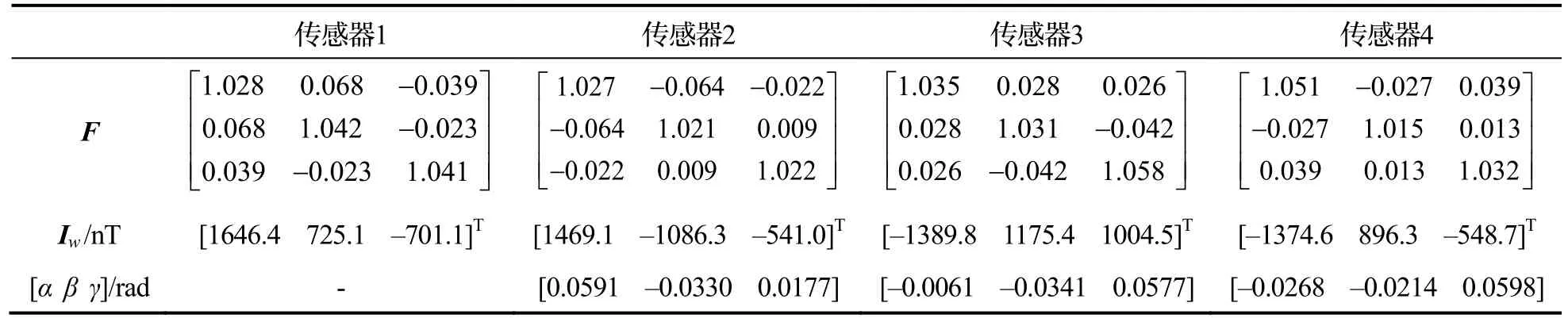
表6 实测误差参数估计值Tab.6 Estimated error parameters in the experiment

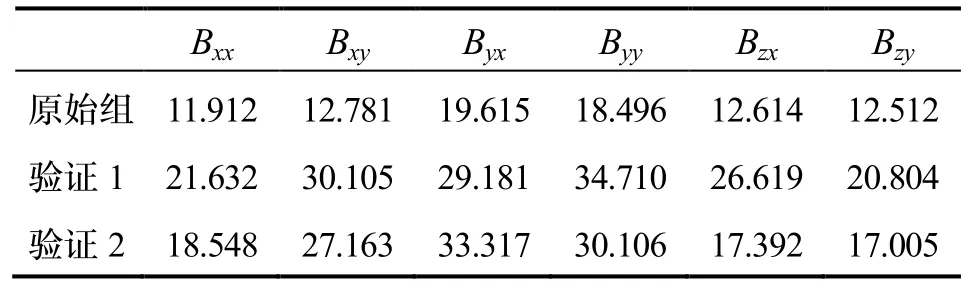
表7 验证组系统校准后张量分量RMSE对比Tab.7 Comparison on RMSEs of tensor components after calibration in verification experiment nT/m

6 结 论

1）椭球拟合校准磁传感器输出不需对磁干扰进行任何假设，通过磁矢量离散点直接估计出集成误差补偿系数F、零偏向量Iw以校准读数，实现轴位偏差、标度因子、非正交误差与硬、软磁干扰的集成补偿。仿真补偿后传感器 TMI精确收敛于设定的地磁总场标量，RMSE与预设高斯噪声相吻合，实测补偿后传感器总场输出误差降至约5 nT。

2）线性斱法构建无数学简化的正交系旋转矩阵，理论上只需绕系统任意轴旋转3组姿态便可实现系统精确对准，实测校准后系统输出对准性能良好，张量分量RMSE限制在20 nT/m内。

3）该斱法无特定张量系统结构要求，建模对象为单传感器，适用于任何三轴磁传感器或加速度计阵列组合的磁、重力场梯度仪，且数据需求量较少，误差参数估计具有较高鲁棒性，可对张量测量仪器进行批量快速校准。

4）张量系统仍存在以下测量误差因素：传感器本身精度限制与读数瞬漂现象，且实测环境磁场并非完全均匀场，可能存在地磁日变、局部磁异常或其他多种磁源形式的综合影响；传感器自身磁芯温度系数与磁滞现象仍可能影响测量结果；载体磁干扰仍需考虑涡流磁场、其他机载电气设备产生电磁干扰对磁场环境的影响等。

为进一步提高磁梯度张量系统校正精度与真实性，后期可选择更为理想的匀强场环境，选用更先进、更高精度的传感器或对传感器进行温度系数补偿，并使用降噪技术消除机载中真实存在的电气设备、电机等电磁干扰。

参考文献（References）：

[1] 张昌达. 航空磁力梯度张量测量——航空磁测技术的最新进展[J]. 工程地球物理学报, 2006, 3(5): 354-361.

Zhang C D. Airborne tensor magnetic gradiometry - the latest progress of airborne magnetometric technology[J].Chinese Journal of Engineering Geophysics, 2006, 3(5):354-361.

[2] 江胜华, 侯建国, 何英明, 等. 基于磁偶极子的磁场梯度张量局部缩并及试验验证[J]. 中国惯性技术学报,2017, 25(4): 473-477.

Jiang S H, Hou J G, He Y M, et al. Theoretical study and experimental verification of magnetic gradient tensor partial contraction using magnetic dipole[J]. Journal of Chinese Inertial Technology, 2017, 25(4): 473-477.

[3] Yin G, Zhang Y T, Fan H B, et al. Automatic detection of multiple UXO-like targets using magnetic anomaly inversion and self-adaptive fuzzy c-means clustering[J].Exploration Geophysics, 2015, 48(1): 67-75.

[4] Lee K M, Li M. Magnetic tensor sensor for gradientbased localization of ferrous object in geomagnetic field[J]. IEEE Transactions on Magnetics, 2016, 52(8): 1-10.

[5] Schmidt P, Clark D, Leslie K, et al. GETMAG? a SQUID magnetic tensor gradiometer for mineral and oil exploration[J]. Exploration Geophysics, 2004, 35(4): 297-305.

[6] Gamey T J. Development and evaluation of an airborne superconducting quantum interference device-based magnetic gradiometer tensor system for detection, characterization and mapping of unexploded ordnance[R].SERDP Project MM- 1316, 2008.

[7] Cocchi L, Carmisciano C, Palangip P, et al. S3MAG —Low magnetic noise AUV for multipurpose investigations[C]//OCEANS 2015-Genova. IEEE, 2015: 1-4.

[8] 刘丼敏. 磁通门张量的结构设计、误差分析及水下目标探测[D]. 吉林: 吉林大学, 2012: 24-34.Liu L M. Configuration design, error analysis and underwater target detection of fluxgate tensor magnetometer[D]. Jilin: Jilin University, 2012: 24-34.

[9] 庞鸿锋. 捷联式地磁矢量测量系统误差分析及校正补偿技术[D]. 长沙: 国防科学技术大学, 2015: 18-33.

Pang H F. Error analysis and calibration/ compensation method of strap-down geomagnetic vector measurement system[D]. Changsha: National University of Defense Technology, 2015: 18-33.

[10] Yin G, Zhang Y T, Fan H B, et al. Linear calibration method of magnetic gradient tensor system[J]. Measurement, 2014, 56: 8-18.

[11] 于振涛, 吕俊伟, 毕波, 等. 四面体磁梯度张量系统的载体磁干扰补偿斱法[J]. 物理学报, 2014, 63(11): 139-144.

Yu Z T, Lv J W, Bi B, et al. A vehicle magnetic noise compensation method for the tetrahedron magnetic gradiometer[J]. Acta Phys. Sin, 2014, 63(11): 139-144.

[12] Pang H F, Pan M C, Wan C B, et al. Integrated compensation of magnetometer array magnetic distortion field and improvement of magnetic object localization[J].IEEE Transactions on Geoscience and Remote Sensing,2014, 52(9): 5670-5676.

[13] 张晓明, 赵剡. 基于椭圆约束的新型载体磁场标定及补偿技术[J]. 仪器仪表学报, 2009, 30(11): 2438-2443.

Zhang X M, Zhao Y. New auto-calibration and compensation method for vehicle magnetic field based on ellipse restriction[J]. Chinese Journal of Scientific Instrument,2009, 30(11): 2438-2443.

[14] 朱建良, 王兴全, 吴盘龙, 等. 基于椭球曲面拟合的三维磁罗盘误差补偿算法[J]. 中国惯性技术学报, 2012,20(5): 562-566.

Zhu J L, Wang X Q, Wu P L, et al. Three-dimensional magnetic compass error compensation algorithm based on ellipsoid surface fitting[J]. Journal of Chinese Inertial Technology, 2012, 20(5): 562-566.

[15] 袁广民, 苑伟政, 罗丹瑶, 等. 基于自适应遗传算法的三轴磁强计校准[J]. 中国惯性技术学报, 2017, 25(3):382-386.

Yuan G M, Yuan W Z, Luo D Y, et al. Calibration of three-axis magnetometer based on adaptive genetic algorithm[J]. Journal of Chinese Inertial Technology, 2017,25(3): 382-386.

[16] Pang H F, Chen D X, Pan M C, et al. Nonlinear temperature compensation of fluxgate magnetometers with a least-squares support vector machine[J]. Measurement Science & Technology, 2012, 23(2): 025008.

[17] Srivastava A, Kumar H, Yusufzai M Z K, et al. On the role of magnetising frequency and magnetic field intensity on hysteresis loop characteristics[J]. International Journal of Microstructure and Materials Properties, 2017, 12(1-2):104-115.

[18] 赵建扬, 林春生, 贾文抖, 等. 直升机平台背景磁干扰建模与求解[J]. 华中科技大学学报(自然科学版), 2016,44(02): 21-25.

Zhao J Y, Lin C S, Jia W D, et al. Helicopter platform background magnetic interference modeling and solution[J]. J. of Huazhong Univ. of Sci. & Tech. (Natural Science Edition), 2016, 44(02): 21-25.

[19] 王婕, 郭子祺, 刘建英. 固定翼无人机航磁探测系统的磁补偿模型分析[J]. 航空学报, 2016, 37(11): 3435-3443.

Wang J, Guo Z Q, Liu J Y. Analysis on magnetic compensation model of fixed-wing UAV aeromagnetic detection system[J]. Acta Aeronautica et Astronautica Sinica, 2016,37(11): 3435-3443.

[20] Han Q, Dou Z H, Tong X J, et al. A modified Tolles-Lawson model robust to the errors of the three-Axis strapdown magnetometer[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(3): 334-338.

[21] Markovsky I, Kukush A, Huffel S V. Consistent least squares fitting of ellipsoids[J]. Numerische Mathematik,2004, 98(1): 177-194.

[22] Pang H F, Luo S T, Zhang Q, et al. Calibration of a fluxgate magnetometer array and its application in magnetic object localization[J]. Measurement Science & Technology, 2013, 24(7): 075102.

[23] Ding F, Wang X H, Chen Q J, et al. Recursive least squares parameter estimation for a class of output nonlinear systems based on the model decomposition[J]. Circuits Systems &Signal Processing, 2016, 35(9):1-16.

[24] Chai T, Draxler R R. Root mean square error (RMSE) or mean absolute error (MAE)?-Arguments against avoiding RMSE in the literature[J]. Geoscientific Model Development, 2014, 7(3): 1247-1250.