基于自适应强跟踪滤波的捷联惯导/里程计组合导航方法

李士心，黄凤荣，邱时前，范超男

（1. 天津职业技术师范大学 电子工程学院，天津 300222；2. 河北工业大学 机械工程学院，天津 300401；3. 北京镭航世纪科技有限公司，北京 100081）

车载定位定向系统是为陆基武器平台提供阵地坐标和方位指向的基准设备，一般采用捷联惯性导航系统（SINS）与里程计（OD）组合模式进行不依赖外界信息的自主导航，以避免战时受外界干扰。对于大型轮式车而言，由于轮胎与地面接触面积大，会导致里程计标度由于轮胎胎压变化、路况变化等原因发生较大变化，无法满足车载定位定向系统给里程计分配的误差要求，从而直接影响系统定位精度。

非线性系统状态估计在组合导航、初始对准等领域具有广泛的应用[1-5]，发展了扩展卡尔曼滤波（EKF）、无迹卡尔曼滤波（Unsented Kalman Filter, UKF）、中心差分卡尔曼滤波（Central Difference Kalman Filter），带渐消因子的强跟踪滤波（STF）、粒子滤波（Particle Filter, PF）、容积卡尔曼滤波（CKF）等多种非线性滤波方法[6-8]。其中，STF提出渐消因子的概念，有效解决了 EKF在模型不确定时的滤波问题；CKF采用球面径向容积准则进行相应的数值积分运算[9]，不仅克服了EKF和UKF在强非线性系统中的应用局限性，而且滤波精度高于CDKF和PF。

为解决里程计标度误差在大型轮式车行驶过程会发生变化导致定位精度变差的问题，本文以 CKF为算法框架，引入STF渐消因子的基本理论，提出了SINS/OD组合导航的自适应ST-CKF算法，并通过仿真分析和跑车试验验证方法的正确性。

1 强跟踪滤波器

假设有如下形式的非线性离散系统：

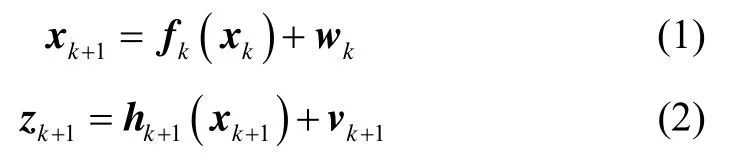
其中：fk和hk+1分别为状态函数和量测函数；与分别为系统状态向量和观测向量；系统过程噪声wk和量测噪声vk互不相关且

STF在EKF的基础上引入渐消因子，实时调整预测误差协方差阵，使滤波残差序列保持相互正交，从而保持对系统状态的跟踪。STF的递推公式为：

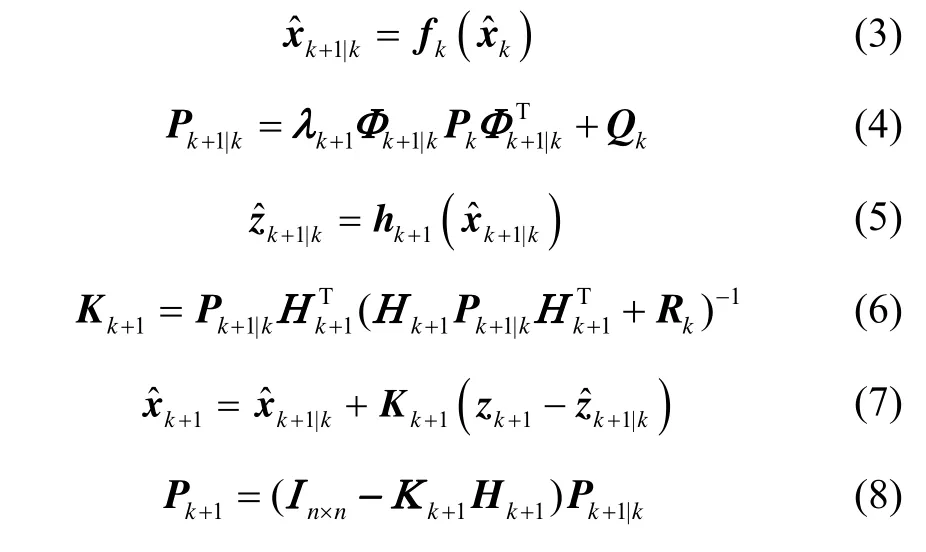
其中，λk+1为渐消因子，In×n为n阶单位阵，

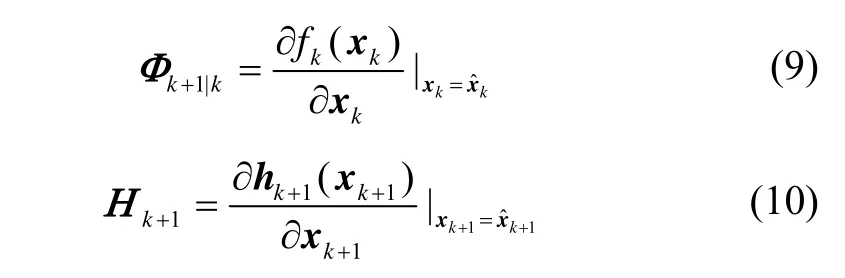
采用次优算法计算渐消因子：

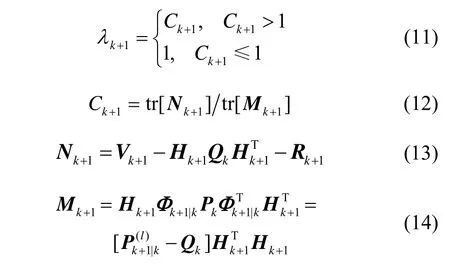
其中，tr[·]为矩阵求迹的算子，为未引入渐消因子的状态预测协方差阵。

为实际输出残差序列的协方差阵，通常是未知的，由下式进行估算：

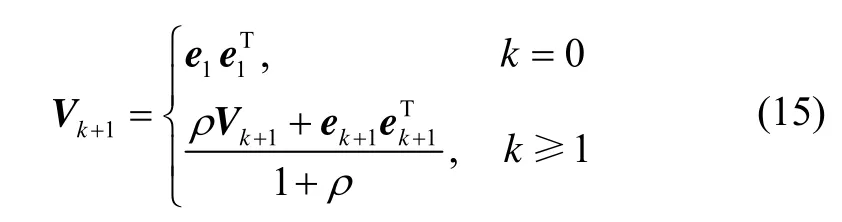
其中，为遗忘因子。

式(13)和式(14)利用了测量函数的泰勒级数展开式计算渐消因子，存在求解雅克比矩阵的问题。根据文献[4]，为避免测量函数的雅克比矩阵数值计算，假设引入渐消因子之前的状态预测误差协方差阵为新息协方差阵为互协方差阵为则式(13)(14)分别有如下的等价表达式：

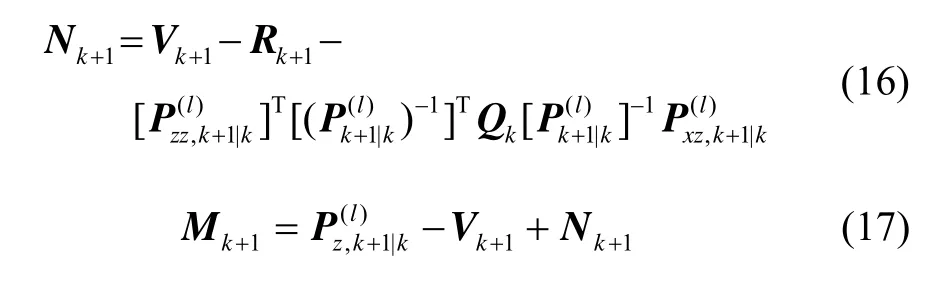
2 容积卡尔曼滤波器

根据文献[6]，CKF算法步骤如下：

1）时间更新

假设k时刻的状态xk的状态误差协方差为Pk，对做Cholesky分解，有：

选择容积点为：

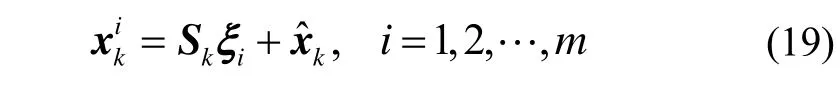
系统状态方程传播后容积点为：

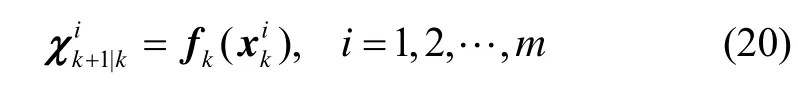
其中，m=2n，且有是点集[1]的第i列。

计算状态预测值：

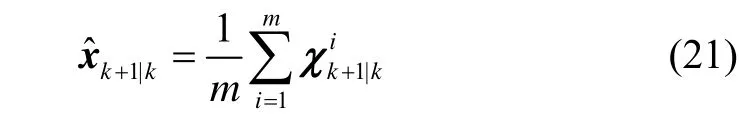
计算误差协方差阵：

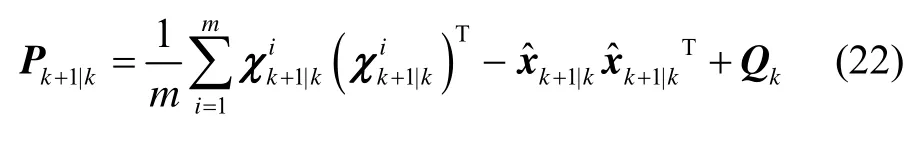
2）量测更新

对Pk+1|k做Cholesky分解：

计算容积点：

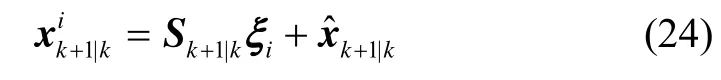
经量测方程传播后的容积点为：

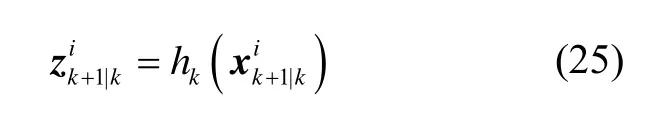
计算观测预测值：

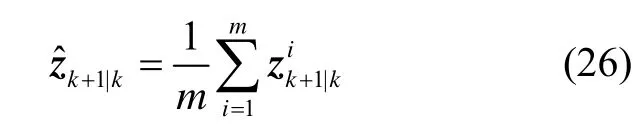
计算量测误差协方差阵：

计算一步预测互相关协方差阵：

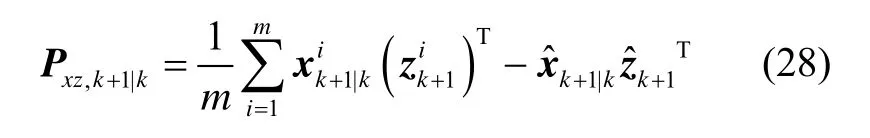
计算滤波增益：

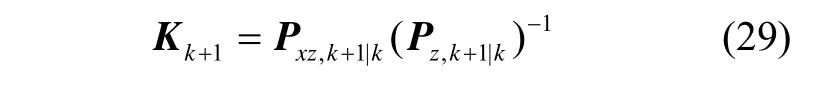
状态估计值：

求取状态误差协方差估计值：

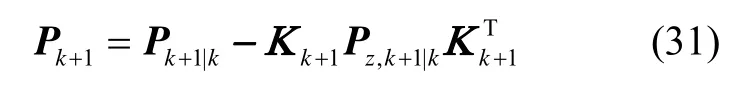
3 自适应强跟踪容积卡尔曼滤波器

STF算法在工程上有以下三点缺陷：1）STF算法基于EKF算法框架，将非线性函数截断近似线性化，对于强非线性系统，计算间隔要设的非常小以减小截断误差；2）需要用数值计算方法计算非线性函数的雅可比矩阵，运算量比较大；3）对于某些不可微非线性函数或时刻点，无法计算雅可比矩阵。

因此，STF数值计算稳定性不佳，甚至对于强非线性系统，容易滤波发散。STF的缺陷都是基于EKF算法框架下的，寻求一种可以代替EKF的算法框架，既能保持STF渐消因子强迫正交的理论优势，又能避免计算雅可比矩阵的繁琐，还能进一步提高非线性函数线性化的计算精度，具有比较强的现实意义。CKF算法过程中不需要计算导数，且具有泰勒展开的三阶精度，故基于CKF算法框架设计强跟踪CKF （ST-CKF）算法，能避免STF的工程应用缺陷，融合STF鲁棒性强和CKF计算精度高的优点，实现工程应用的目的。

ST-CKF的算法步骤如下：

1）时间更新

由式(18)～(22)计算没有引入渐消因子的状态预测协方差阵进行Cholesky分解：

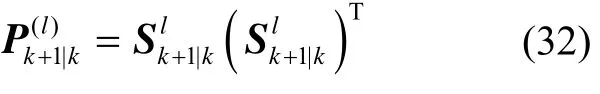
2）计算渐消因子

由式(23)～(28)计算没有引入渐消因子的量测

误差协方差阵和一步预测互相关协方差阵

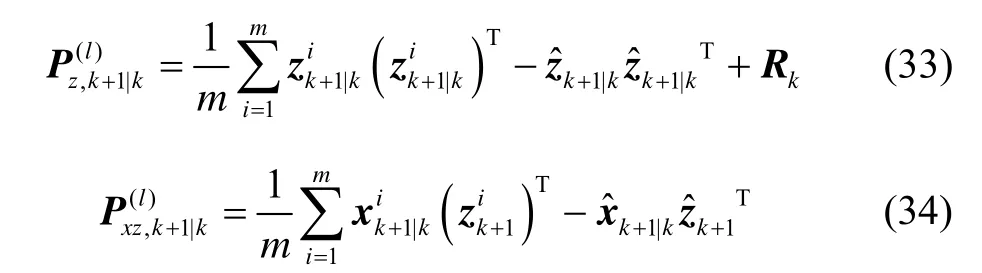
然后由式(32)～(34)、式(11)～(17)计算渐消因子λk+1。

3）量测更新

根据加入渐消因子λk+1的状态xk+1的统计特性由式(24)求取相应加入渐消因子的容积点以此重复式(25)～(31)的流程求得状态估计和Pk+1。

4 SINS/OD组合导航卡尔曼滤波模型

本文选取SINS的姿态角误差φE、φN、φU，水平速度误差δvE、δvN，经纬度误差δλS、δLS，陀螺常值漂移εx、εy、εz，加速度计零偏∇x、∇y、∇z，里程计推算经纬度误差δλD、δLD，里程计标度因数误差δKD，里程计方位安装偏角φα作为状态变量，建立17维的SINS/OD组合导航状态方程；选取 SINS解算经纬度与里程计推算经纬度之差作为量测构建量测方程。误差模型的建立与推导过程参看文献[10]。

SINS/OD组合导航的状态向量为：

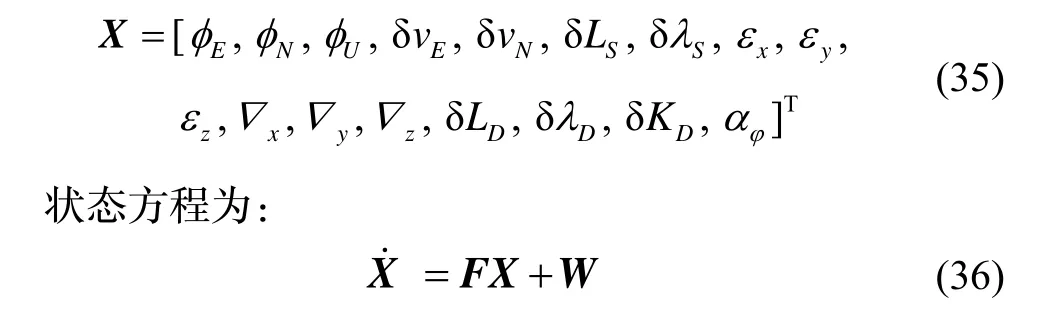
式中：W为3只陀螺漂移和3只加速度计零偏测量噪声，F为系统状态矩阵，见式(37)。的第i行第j列元素，vD为里程计输出速度。

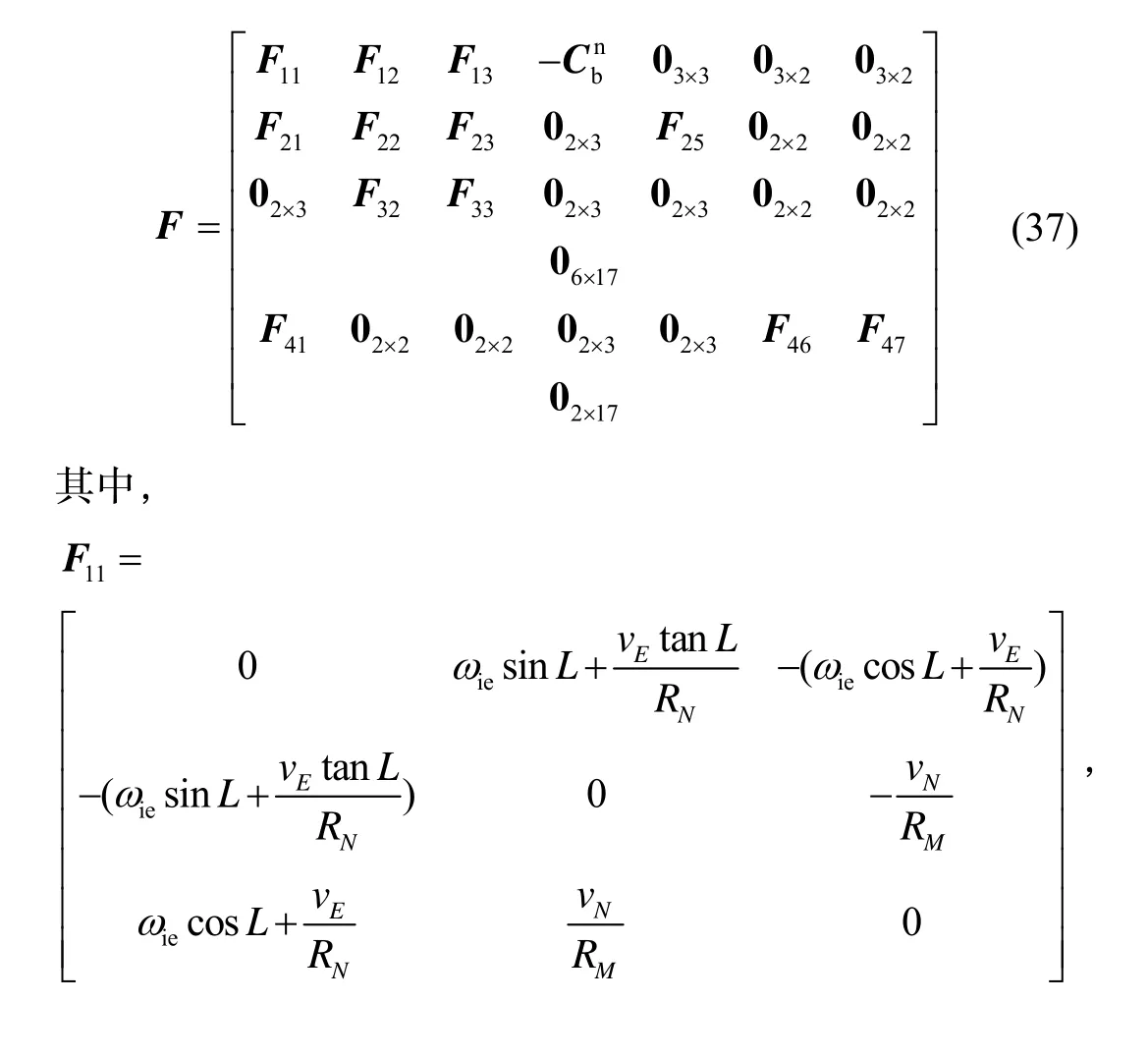
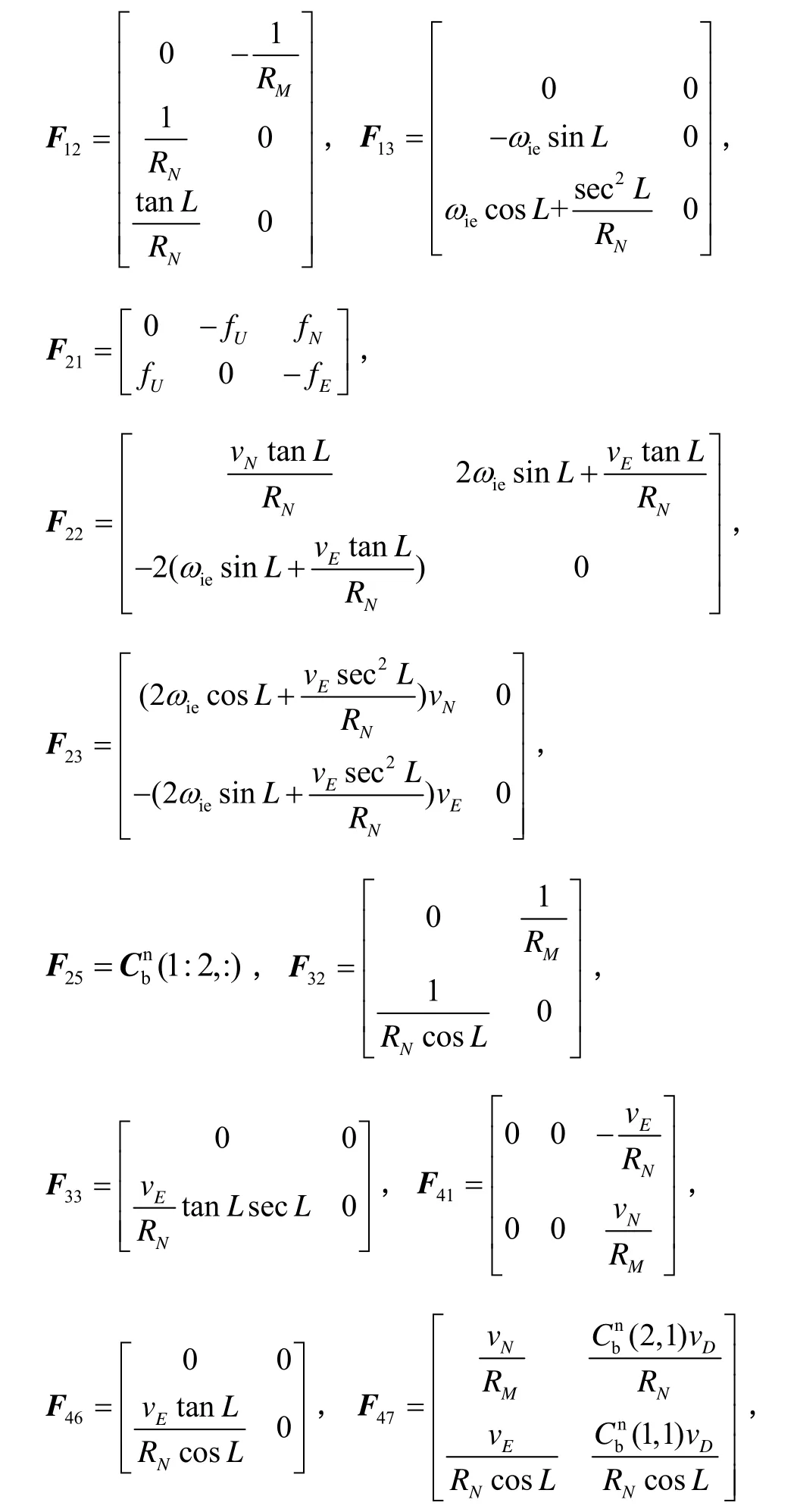
量测方程为：

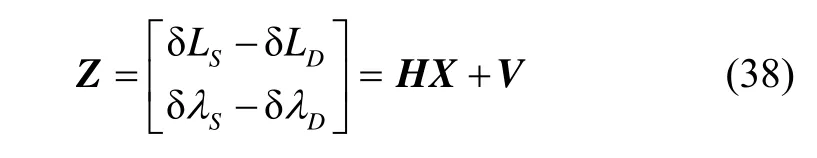
其中，V为里程计推算纬度和经度的量测噪声，

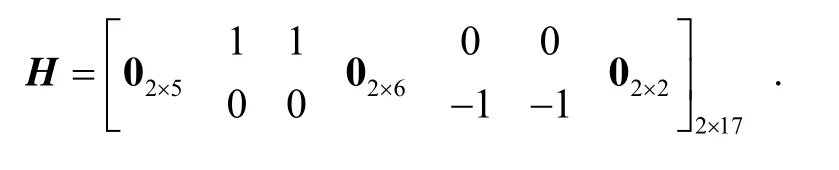
5 仿真分析和试验验证

分别采用EKF、STF、ST-CKF进行SINS/OD组合导航的仿真分析，滤波性能的好坏可以通过 SINS/OD组合导航的定位精度、里程计安装偏角和标度误差的跟踪性能来衡量。

假设：3个陀螺的常值漂移均为0.01 (°)/h，随机白噪声标准差为0.01 (°)/h；3个加速度计的零偏均为0.05 mg，随机白噪声标准差为0.05 mg；初始水平姿态角误差 0.01°，初始航向误差 0.1°，初始水平速度误差和初始经纬度误差均为0；载车初始位置为北纬40°，东经 118°，初始时刻方位角为 45°，俯仰角为 0°，横滚角为0°，以20 m/s的速度匀速行驶，行驶时间为 900 s；里程计标度误差设为0.01，方位安装偏角设为 0.05°。考虑大型轮式车的实际应用背景进行以下两种情况仿真分析：

1）假设里程计标度误差δKD受路况变化影响发生了突变，在300s时由0.01阶跃到0.02；

2）假设里程计标度误差δKD受胎压变化影响发生了渐变，在300s时开始到600s结束，由0.01斜坡变化到0.02。

以上两种情况分别采用EKF、STF、ST-CKF对δKD进行估计，里程计标度误差阶跃变化和斜坡变化的跟踪曲线如图1和图2所示。

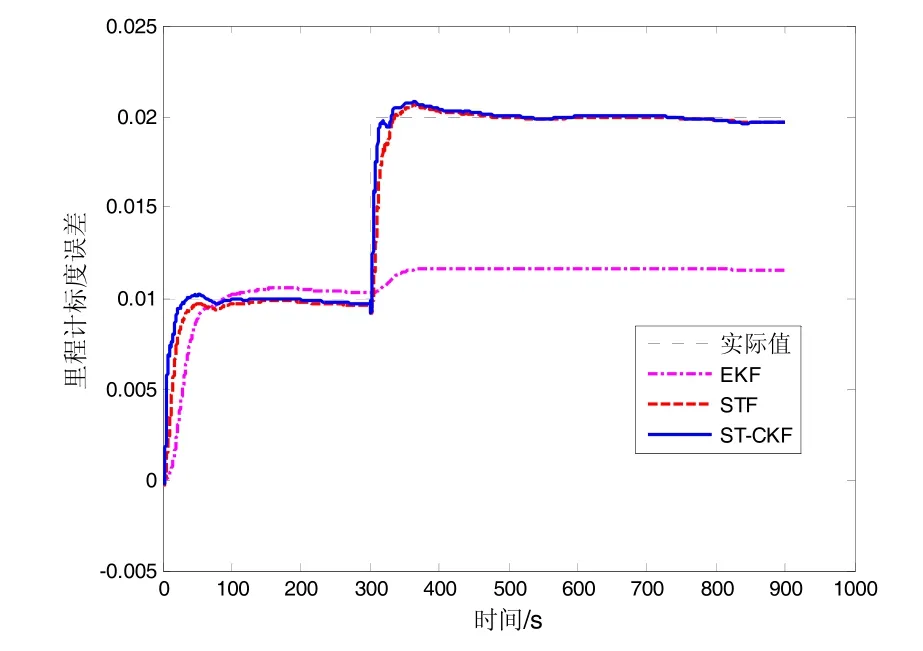
图1 EKF、STF和ST-CKF算法对δDK 阶跃变化的跟踪曲线Fig.1 Step change tracking curve ofδDK using EKF, STF and ST-CKF algorithms

图2 EKF、STF和ST-CKF算法对 δKD线斜坡变化的跟踪曲Fig.2 Ramp change tracking curve ofδDK using EKF, STF and ST-CKF algorithms

由图1～2中曲线不难看出，EKF在运行一段时间后可以有效地估计出δKD的常值量，然而在随后误差发生幅度较大的突变或渐变时，EKF失去了跟踪能力。因此对于 SINS/OD组合导航系统而言，EKF可以在δKD为常值或变化不大的情况下使用，作为一种在线自主标定方法是有效的，而STF和ST-CKF无论对误差的突变还是渐变都具有很强的跟踪能力。

为验证ST-CKF的工程实用性，进行了大型轮式车的跑车试验。试验采用的激光陀螺定位定向系统惯性元件精度为：陀螺零偏稳定性＜0.015 (°)/h，陀螺零偏重复性＜0.005 (°)/h，加速度计零偏稳定性和重复性＜0.05 mg。试验设计的行车路线如图3所示（仅示意变化量），行车里程220 km，包括去程和回程共2个航程。试验前静止对准3 min，试验过程中以GPS位置信息作为参考基准，GPS定位精度＜2 m。分别采用EKF、STF和ST-CKF对跑车过程中录取的激光陀螺定位定向系统和里程计原始数据进行离线仿真。

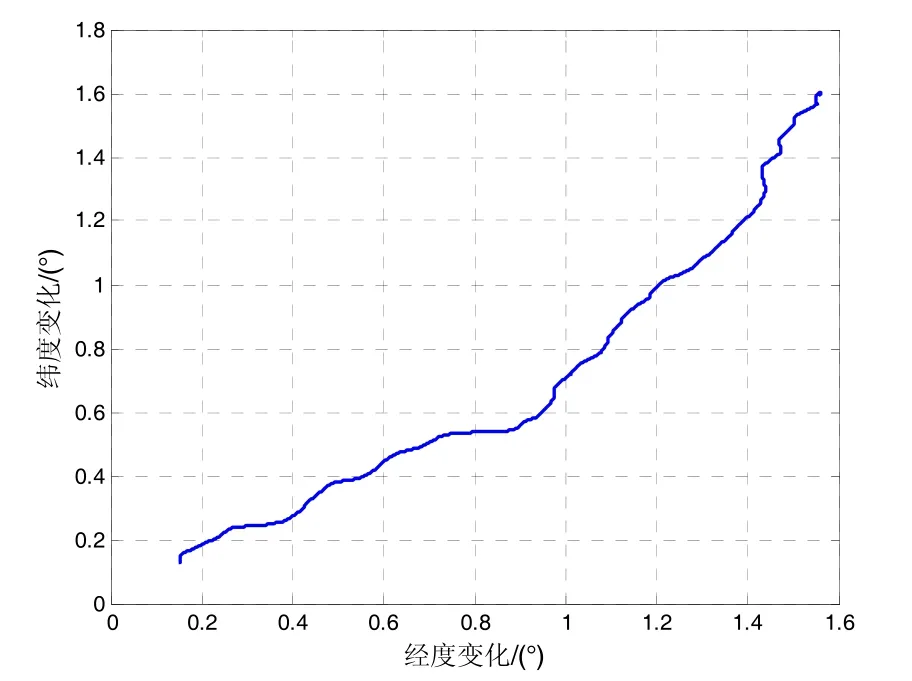
图3 行车轨迹Fig.3 Trajectory of vehicle

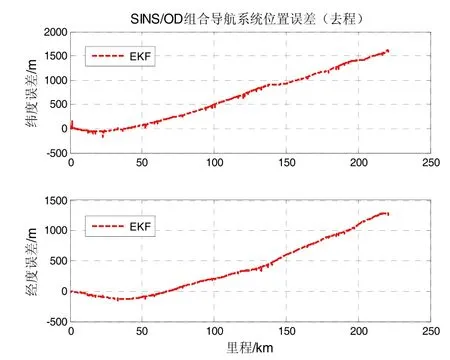
图4 第1航程EKF算法的位置误差曲线Fig.4 Position error curve of test-1 using EKF algorithm

图5 第2航程EKF算法的位置误差曲线Fig.5 Position error curve of test-2 using EKF algorithm

两个航程的EKF位置误差试验结果如图4和图5所示，STF和ST-CKF位置误差试验结果如图6和图7所示，图中毛刺为GPS跳数所致。由图4和图5可以看出，由于EKF无法实时跟踪里程计标度的变化，去程定位误差最大达到了 1617 m，回程最大误差为619 m，定位误差＞7‰D（其中，D为里程），根本没有发挥出惯性元件的使用精度。由图6和图7可以看出，STF和ST-CKF均达到了＜1.5‰D的定位精度，对比可以看出ST-CKF对STF的改进，去程定位误差最大由282 m提升到128 m，回程定位误差最大由180 m提升到111 m，使得SINS/OD组合导航系统的定位精度由1.3‰D提高到0.6‰D，ST-CKF比STF更进一步消除了里程计误差的影响，达到了惯性元件的理论精度。

图6 第1航程STF和ST-CKF算法的位置误差曲线Fig.6 Position error curve of test-1 using STF and ST-CKF algorithms

图7 第2航程STF和ST-CKF算法的位置误差曲线Fig.7 Position error curve of test-2 using STF and ST-CKF algorithms

去程和回程的里程计标度误差和方位安装偏角ST-CKF估计曲线如图8和图9所示。由图8可以看出，里程计标度误差在试验过程中近似斜坡缓慢变化了大约 0.015；由图9可以看出，里程计标度误差在190 km处由于路况（高速转入市内公路）改变而发生了明显突变。里程计标度的实际变化包括了仿真分析的两种情况，说明了仿真分析的合理性。由图8分析，如果不能对里程计误差进行实时估计补偿的话，会造成约220 000×0.015÷2=1650 m的位置误差，与EKF去程定位误差最大1617 m相符，这也反映了里程计标度误差自适应补偿的必要性。

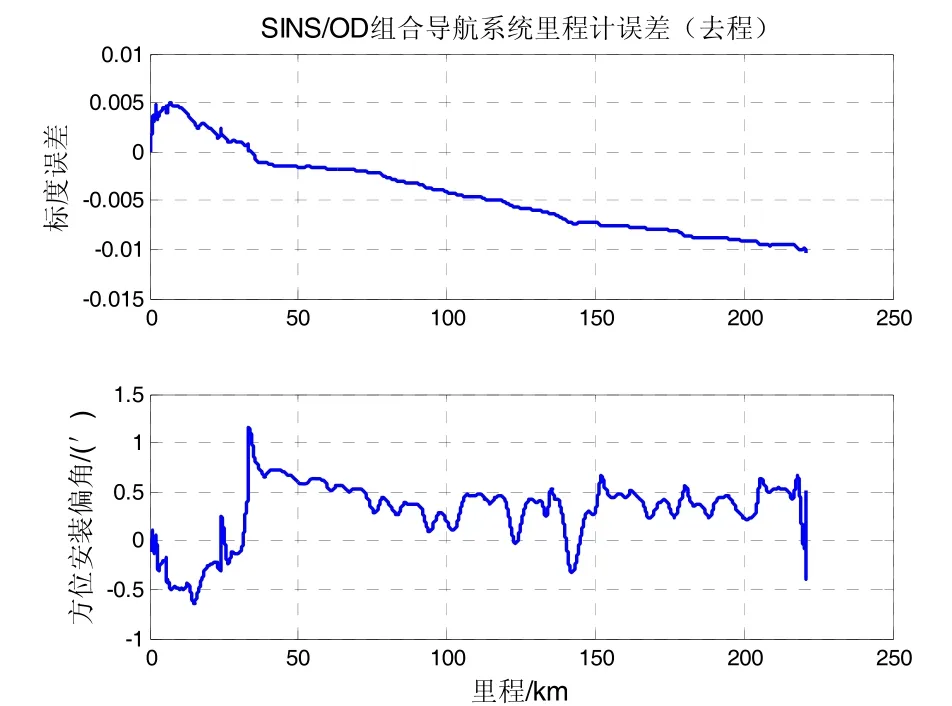
图8 第1航程ST-CKF算法里程计误差估计曲线Fig.8 OD’s error estimated curve of test-1 using ST-CKF algorithm

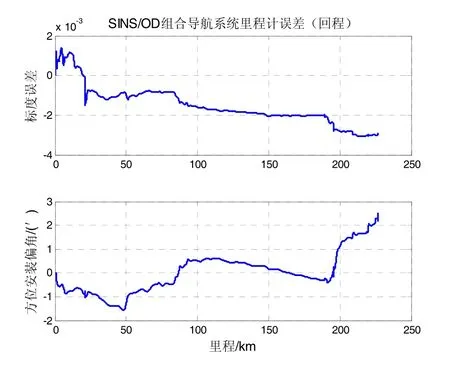
图9 第2航程ST-CKF算法里程计误差估计曲线Fig.9 OD’s error estimated curve of test-2 using ST-CKF algorithm

6 结 论

本文针对EKF在SINS/OD组合导航误差模型中对里程计误差模型描述不准确时难以实时跟踪误差变化以及STF在工程应用上的局限性，用CKF替代EKF的算法框架，引入STF渐消因子的基本理论，提出了SINS/OD组合导航的自适应ST-CKF算法，并进行了仿真分析和跑车试验。仿真证明STF和ST-CKF具有实时跟踪里程计误差变化的能力，验证了算法有效性。跑车试验结果表明，基于自适应STF的组合导航方法能有效估计速度辅助传感器的时变误差，所提出的ST-CKF算法进一步提高了误差估计精度，有效解决了里程计标度误差在大型轮式车行驶过程发生变化导致定位精度变差的问题。另外，本文方法不仅适用于陆用定位定向导航，还可以推广到SINS/DVL组合的航海导航领域[11-12]，具有良好的应用前景。

参考文献（References）：

[1] Zhang L, Yang C, Chen Q W, et al. Robust H-infinity CKF/KF hybrid filtering method for SINS alignment[J].IET Science, Measurement & Technology, 2016, 10(8):916-925

[2] Cui B B, Chen X Y, Xu Y, et al. Performance analysis of improved iterated cubature Kalman filter and its application to GNSS/INS[J]. ISA Transactions, 2017, 66: 460-468.

[3] Zhou W D, Hou J X, Liu L, et al. Design and simulation of the integrated navigation system based on extended Kalman filter[J]. Open Physics, 2017, 15(1): 182-187.

[4] 王小旭, 赵琳, 薛红香. 强跟踪CDKF及其在组合导航中的应用[J]. 控制与决策, 2010, 25(12): 1837-1842.

Wang X X, Zhao L, Xue H X. Strong tracking CDKF and application for integrated navigation[J]. Control and Decision, 2010, 25(12): 1837-1842.

[5] 赵小明, 赵帅, 郭永刚, 等. 基于强跟踪滤波的车载行进间对准[J]. 中国惯性技术学报, 2015, 23(2): 141-144.Zhao X M, Zhao S, Guo Y G, et al. In-motion alignment based on strong tracking filter[J]. Journal of Chinese Inertial Technology, 2015, 23(2): 141-144.

[6] Arasaratnam I, Haykin S. Cubature Kalman filters[J].IEEE Transactions on Automatic Control, 2009, 54(6):1254-2169.

[7] Pasha S A, Hoang D T, Vo B N. Nonlinear baysian filtering using the unscented linear fractional transformation model[J]. IEEE Transactions on Signal Processing,2013, 58(2): 477-489.

[8] Gustafsson F. Particle filter theory and practice with positioning applications[J]. IEEE Aerospace and Electronic Systems Magazine, 2015, 25(7): 53-82.

[9] 刘万利, 张秋昭. 基于 Cubature卡尔曼滤波的强跟踪滤波算法[J]. 系统仿真学报, 2014, 26(5): 1102-1107

Liu W L, Zhang Q Z. New strong tracking filter based on cubature Kalman filter[J]. Journal of System Simulation,2014, 26(5): 1102-1107

[10] 赵洪松, 缪玲娟, 沈军. 捷联惯导/里程计高精度组合导航算法[J]. 兵工学报, 2014, 35(4): 433-440.

Zhao H S, Miao L J, Shen J. High accuracy algorithm for SINS/Odometer integrated navigation system[J]. Acta Armamentarii, 2014, 35(4): 433-440.

[11] Gao W, Li J C. Adaptive Kalman filtering for the integrated SINS/DVL system[J]. Journal of Computational Information Systems. 2013, 16(9): 6443-6450.

[12] Wang L, Cheng X H, Li S X, et al. Adaptive interacting multiple model filter for AUV integrated navigation[J]. Journal of Chinese Inertial Technology, 2016, 24(4): 511-515.