面向多飞行器的一致性协同估计方法
杨 明,赵恩娇,晁 涛,王松艳
(哈尔滨工业大学 控制与仿真中心,哈尔滨 150080)
随着空战环境日益复杂,作战武器性能日益提高,多飞行器协同作战已成为当今复杂空战中主要的作战方式[1]。为了进一步扩大防御面积,提高防御能力,很多国家将多飞行器协同拦截作为一种新式的防御战术[2],其中,协同拦截机动目标技术是现代飞行器防御系统研究的热点,更是未来防御技术发展必须解决的关键技术之一。信息交换与共享是多飞行器协同作战策略能否有效实施的关键,也是协同控制技术面临的难题之一。在信息共享的基础上,飞行器以保证整体任务性能为前提,调整个体行为实现协同。协同拦截的关键技术是通过某种协调机制实现飞行器间的高度配合,精确拦截高价值的机动目标。
要实现多飞行器对机动目标的协同拦截,首先要利用飞行器各自对目标的估计信息,并通过机间数据链网络完成对目标的协同估计,以满足协同拦截的要求。在这一过程中,目标状态估计算法是核心和关键。在复杂的战场环境中,网络通信条件易受到电磁干扰,网络拓扑结构会不断发生变化,传统的集中式融合估计方法已不再适用于这种情况。由于多智能体一致性理论在信息交换、分布式协调等方面表现出色,近年来在分布式状态估计方法中得到广泛的应用[3-5]。分布式估计算法能够综合利用多个传感器的观测信息,提高传感器网络参数估计的精确度和系统的鲁棒性,并且这种算法仅使用局部信息,不需融合中心,最终所有传感器的估计值趋于一致,因此成为传感器网络应用中所广泛采用的信息处理技术之一[6]。
随着一致性估计算法的广泛应用,发展具有分布式结构的协同估计算法在多飞行器协同制导和控制中都具有重要的意义。
在飞行器的末制导过程中,尤其是在制导的末段,目标的逃逸机动是影响制导精度的主要因素。针对机动目标的跟踪,卡尔曼滤波技术是一种常用的方法,但其需要精确知道系统模型和特性,不利于在飞行器攻防对抗过程中使用,需要探索不依赖于目标机动模型的目标信息估计新方法。扩张状态观测器(Extended state observer, ESO)可对系统中的不可测状态以及未知扰动进行观测,是自抗扰控制等非线性控制技术的重要组成部分,在干扰估计[7]、故障诊断中发挥着重要作用,在很多工程领域得到应用[8-10]。由于扩张状态观测器理论日趋成熟以及其表现出的种种优势,进一步探索扩张状态观测器在多飞行器协同估计中的应用具有重要的工程意义。
针对上述讨论中存在的问题,本文提出了一种适用于多飞行器拦截机动目标的一致性协同估计方法。基于扩张状态观测器的工作原理,将目标的状态视作扰动,并扩张成为新的一阶状态,再利用特定的非光滑非线性误差反馈,选择适当的观测器参数,得到系统所有状态的观测值。在此基础上利用一致性理论为各飞行器设计一致性估计协调控制量,通过局部信息交换使得各飞行器得到一致的估计量,将得到的机动目标的一致性估计值在制导律中进行相应的补偿,从而保证各飞行器能够同时拦截机动目标。最后验证了本文方法的有效性。
1 预备知识及问题描述
1.1 图 论
多个飞行器的间通信关系可以用图来描述,非空节点的集合为其节点数目称为阶,边的集合为加权邻接矩阵其中aij表示以i为起点,j为终点的边的权值。根据边有无方向,图分为有向图和无向图。无向图的邻接矩阵是对称的,从节点i到节点j之间有一条边,也就是说有向图的邻接矩阵一般是不对称的,且节点之间的边是有方向的。节点j称作节点i的邻居,而节点i的所有邻居用集合可以表示为
1.2 一致性理论
本文利用多智能体一致性理论解决多飞行器的协同估计问题,这里先给出一致性理论的相关概念。
考虑由n个多智能体组成的一组多智能体系统。智能体的动力学模型为:
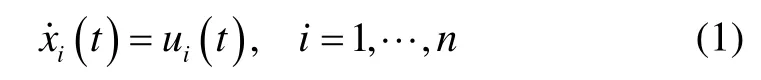
式中,为状态,为控制输入。
定义1 如果对于任意初值,智能体的状态都满足:则称多智能体系统(1)实现渐近一致。
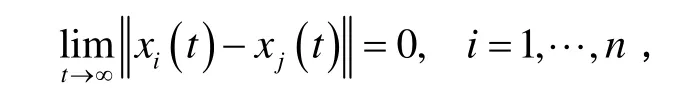
定义2如果对于任意初值,任意智能体的状态都能收敛到所有初始动态的平均值,即:
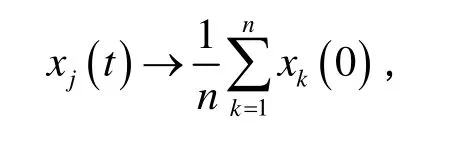
则称多智能体系统实现平均一致性。
1.3 问题描述
本文的研究目的是为多飞行器网络中的各个飞行器设计一个分布式协同估计策略。假设通信网络由n个飞行器组成,并将飞行器序号顺序标记为从1到n,各个飞行器配备主动雷达导引头。
考虑平面内多个飞行器协同拦截单个高价值机动目标的情况,平面几何关系如图1所示。XOY为惯性参考坐标系;M代表飞行器,下角标为飞行器的编号,即Mi代表第i个飞行器;T为目标;带有下脚标i和t的变量分别表示第i个飞行器和目标的状态量;V、a、分别代表飞行器的速度、法向加速度、弹道倾角、视线高低角、弹目相对距离。
由图1中的飞行器和目标间的相对运动关系,以第i个飞行器为例,可以得到如下第i个飞行器与目标的相对运动关系:
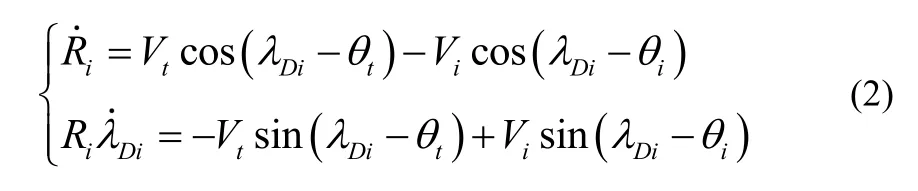
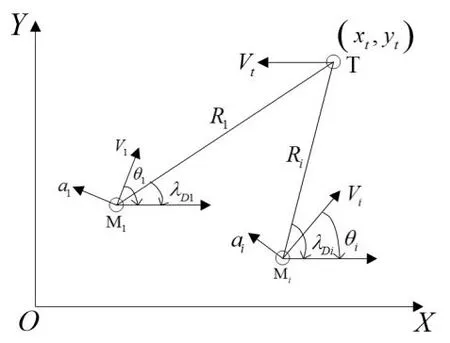
图1 多飞行器与目标的相对运动关系Fig.1 Relative motion between multi-aircraft and target
为便于推导,令个飞行器与目标的相对运动方程求导可以得到飞行器与目标的相对运动模型:
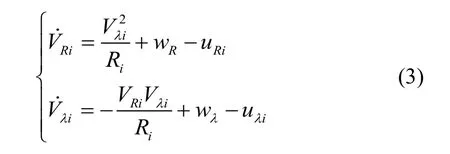
式中:分别是目标加速度和第i个飞行器加速度在视线方向上的分量;分别是目标加速度和第i个飞行器加速度在视线法向上的分量。
在多飞行器协同作战过程中,当多个飞行器协同拦截空中来袭机动目标时,需要对目标状态进行分布式估计和跟踪。构建多飞行器分布式协同估计系统原理框图,如图2所示。首先,各飞行器利用导引头采集观测目标的数据信息;然后,根据导引头信息,采用扩张状态观测器实现局部的目标状态估计,并通过飞行器网络间估计信息的交互协调实现目标的联合估计,而不是将这些数据信息传送到融合中心。相对于传统集中式目标状态估计,分布式估计方法不会过分依赖系统特定的融合控制中心。通信网络中各飞行器的分布式计算能够加快数据的处理速度,因此目标状态跟踪的实时性会得到很大的提高,并且系统的可靠性也会有所增强。此外,在目标状态的估计中,分布式方法可以很好地适应网络中的很多干扰,如丢包、时延等。
在分布式一致性估计器中,每个飞行器各自对目标状态进行估计,并只与其邻居飞行器进行通信。因为各飞行器估算得到的状态值是各自视线坐标系下的目标状态,所以需要经过坐标转换而转换到统一坐标系下进行一致性估计。
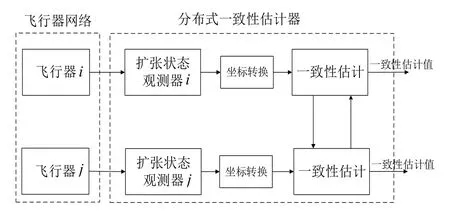
图2 多飞行器协同估计原理Fig.2 Cooperative estimation principle
2 基于ESO的分布式一致性估计器设计
由图2的多飞行器协同估计原理框图可知,基于一致性的协同估计器设计包括以下两方面内容:单个飞行器对目标机动加速度的估计;与邻居飞行器进行信息交互,使各飞行器的估计值趋于一致。假设飞行器携带主动雷达导引头并具有通信能力,可实时与邻接的飞行器进行信息交换。
2.1 基于ESO的目标加速度估计
在采用协同制导律的前提下,为每枚飞行器设计ESO估计机动目标加速度,实现对机动目标的跟踪。
本节根据前文建立的非线性弹目相对运动学方程,将系统中的机动目标加速度当作不确定性并扩张成新的一阶状态,然后设计二阶扩张状态观测器来观测系统状态,从而得到机动目标加速度的估计值,为后续协同估计算法的设计提供必要条件。
根据式(2)所描述的弹目相对运动关系,依然以第i个飞行器为例,对式(2)求导可得:
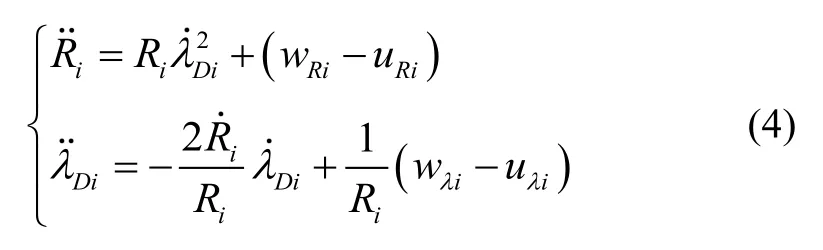
式(4)即为含有飞行器和目标机动信息的弹目相对运动模型。在协同拦截问题的研究中,假设目标只在视线法向进行机动。各飞行器提高制导精度的关键在于通过控制视线角速率令其趋近于零,从而实现协同拦截,这里需要估计的是的值。
取状态变量则上述弹目相对运动方程可化为一个一阶线性时变微分方程:
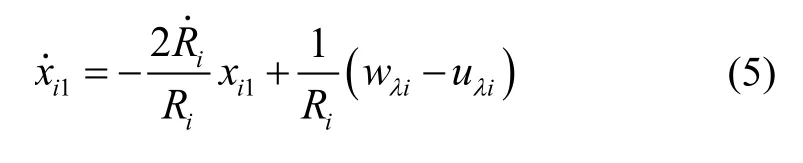
令为模型中的已知分量,为模型中的未知分量,并设则式(5)可以写为:
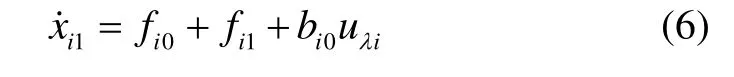
将模型中的未知分量fi1扩张为一阶状态,即并设这里的ψi也是未知量,那么式(6)可写为
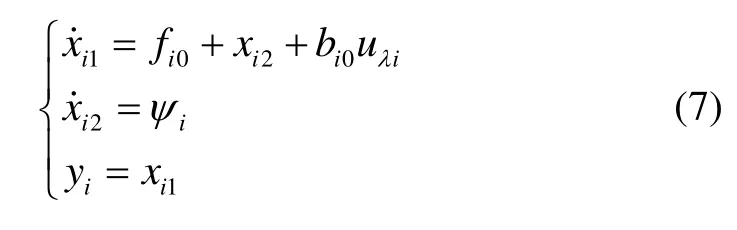
根据ESO理论,对式(7)设计如下的ESO:
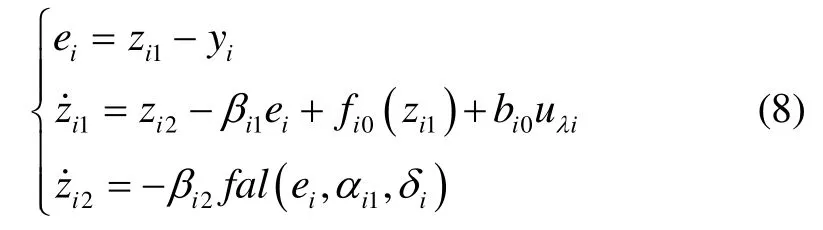
式中:为ESO参数;z1i是x1i的观测值,z2i是x2i的观测值,这样就可得到模型中未知分量的估计值进而得到机动目标加速度的估计值
2.2 多飞行器协同一致性估计器
在2.1节设计的通过ESO来实时估计目标加速度的方法基础上,本节给出分布式一致性估计器的设计方法,实现多枚飞行器对来袭机动目标加速度的协同估计。
利用扩张状态观测器估计得到的是视线坐标系下的目标加速度。在设计一致性估计算法时,需要将各飞行器估算的到的结果统一转换到目标运动的弹道坐标系下。下面给出弹道系下飞行器一致性估计分量:
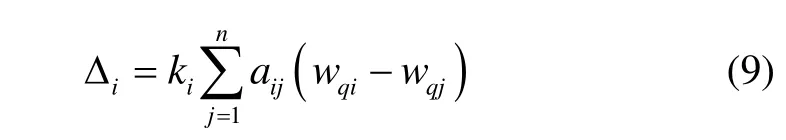
式中:wqi和wqj分别为在目标弹道系下第i枚飞行器和第j枚飞行器转换得到的的估计值;为一致性控制增益;aij为通信网络内任意两飞行器之间的权值。根据视线系和弹道系坐标转换关系,得到视线系飞行器一致性估计分量:
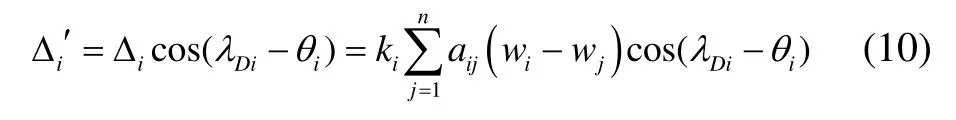
一致性估计分量表达式与一致性控制协议类似,为了达到多个飞行器的估计状态一致,控制增益可以选取为任意的正数。本文的关键就是设计合理的一致性估计器,保证各飞行器给出一致性估计值,并且估计值趋近于真实值。下面给出主要定理。
定理 1 如果飞行器网络拓扑结构是连通的,那么采用如下一致性估计器:
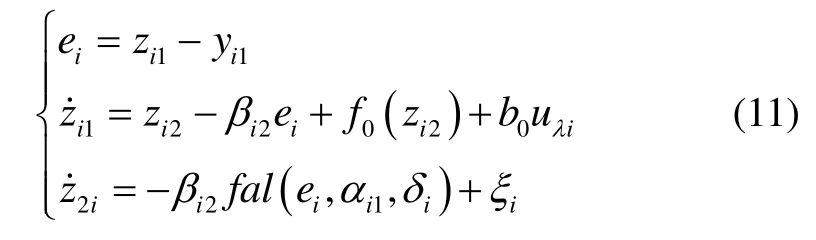
式中:一致性估计器可使得各飞行器给出一致的估计值,并且趋近于真实值。
下面对本文所设计的一致性估计器进行误差分析和估计,并利用Lyapunov函数方法证明系统的稳定性,给出观测器参数的选取原则。
证明 记由式(7)(11)可得:
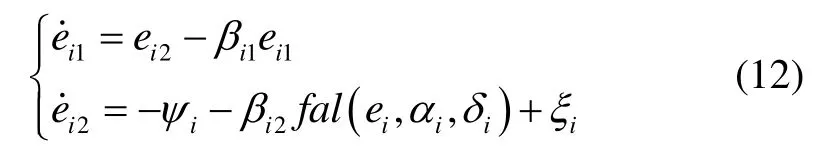
其中,iψ有界,即
以第i枚飞行器的一致性估计器为例,利用将坐标平面分为5个区域[11],如图3所示。
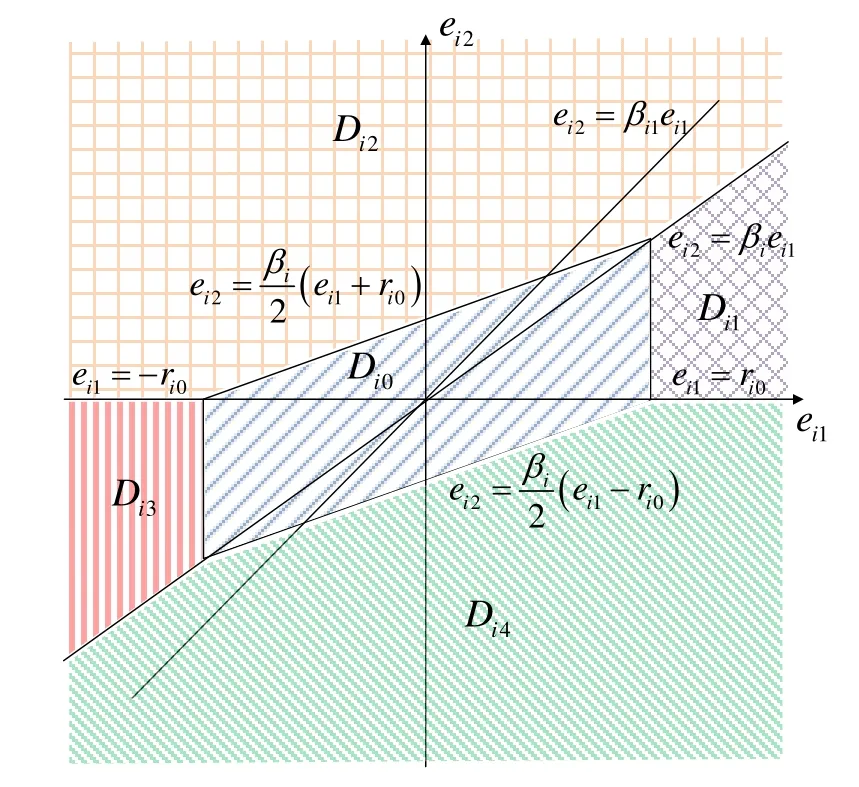
图3 误差平面分区图Fig.3 Division graph of error plane
各区域可具体表示如下:
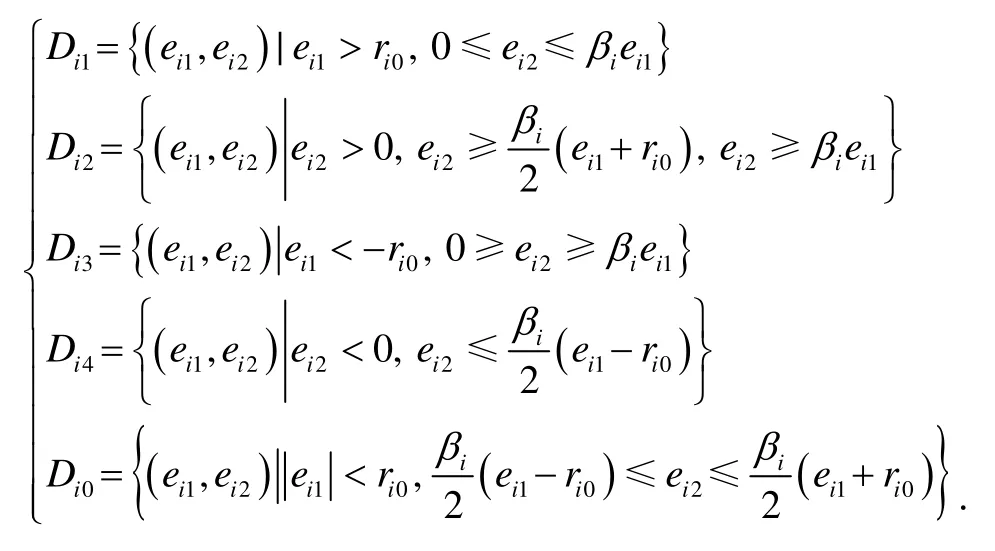
根据以上5个分区,分别构造以下分段光滑的正定Lyapunov函数:
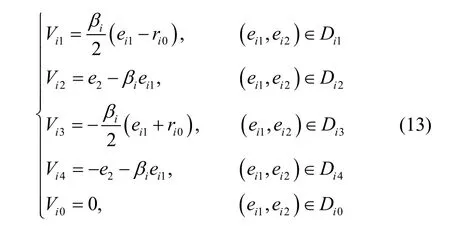
由式(13)可知,函数在除以外的全平面内正定且连续。在固定的情况下,选择合适的参数值使得除函数沿着系统(12)的轨线的导数有即:
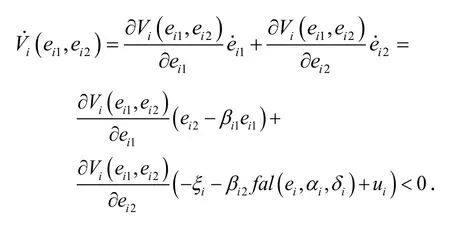
因此系统(12)是稳定的,并且估计误差系统(12)的轨线均被平面区域Di0所吸引,使得估计误差最终收敛于区域Di0。由误差平面分区图3可知,误差区域的大小由ri0和βi决定,可以看出,ri0越小,误差区域Di0的面积就越小。
以为例,给出满足约束条件的求解过程。在区域Di1内,由于则:
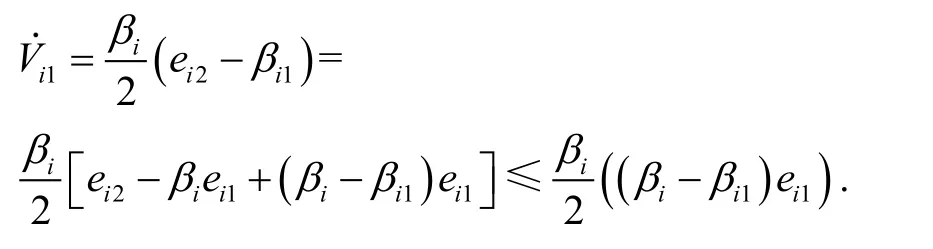
由于存在足够小的正数可以得到:
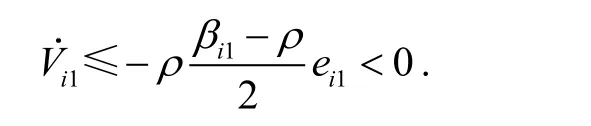
类似地,可以得到区域内对应的Lyapunov函数的导数分别小于0,即:
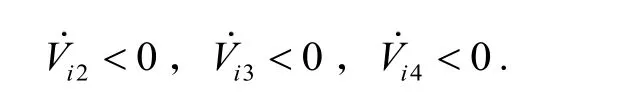
对于系统构造的分段光滑的正定 Lyapunov函数式(13),由于除Di0外的每个Lyapunov函数的导数分别小于零,因此本文设计的一致性估计器是稳定的,并且收敛到区域Di0。证毕。
本文研究的分布式目标状态估计系统具有固定的拓扑结构,并且网络拓扑图是连通的,相邻飞行器之间都会进行数据信息的交换。通过一致性协调控制相互传递和转化各自的估计信息,最终所有飞行器的估计值逐渐趋于相同,即系统达到了一致,并趋近于真实值。
注1由于扩张状态观测器的非线性函数采用了完整的分段形式,在区域的推导过程中,需要对两种情况分段进行讨论,方法类似,这里不再赘述。
3 仿真校验
为了验证本文设计的一致性估计方法的有效性,选取了三种不同的目标机动形式,分别对本文设计的一致性协同估计方法进行仿真分析。采用文献[12]设计的协同制导律,将一致性估计值补偿到制导律中,得到第个飞行器的法向加速度指令:
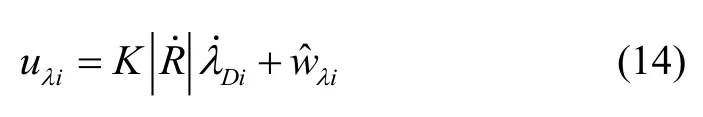
式中:为应用本文设计的一致性估计器估计得到的一致性目标加速度值。
目标的三种机动形式如表1所示,假设目标只在法向机动,切向不机动,即只改变速度方向不改变速度大小。
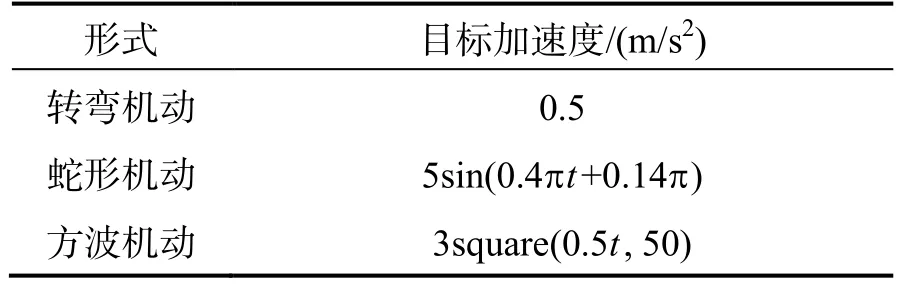
表1 目标的机动形式Tab.1 Maneuver forms of the target
仿真中采用三枚飞行器对一枚机动目标进行协同拦截。飞行器和机动目标的初始状态如表2所示。
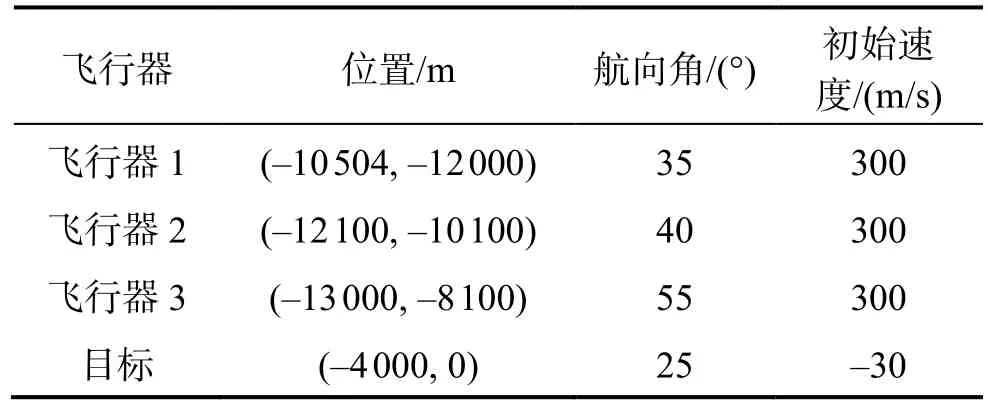
表2 飞行器和目标的初始状态参数Tab.2 Initial state parameters of flight vehicles and target
假设三个飞行器间的可以两两进行相互通信,在飞行过程中能够交换彼此的估计信息,从而进行一致性状态估计。
一致性估计器中参数的选取直接影响了对目标状态的估计精度,β i1和βi2作为估计器增益影响单个飞行器对目标状态的观测精度,增加β i1和βi2能够提高估计精度和速度,但是容易造成振荡。δi的选取决定了式(11)中分段函数线性区大小,适当减小δi的取值,减少线性区的大小,可以提高估计精度,但容易造成振荡。ki为一致性估计器的协调增益,增加ki,可以提高各个飞行器估计值的一致性收敛速度,但过大的容易造成估计值产生较大振荡从而使估计器失效。因此应综合考虑系统的估计精度、动态响应速度等因素。以第1枚飞行器为例,参数取值分别为β11=40,其他飞行器的参数取值原则类似。
采用上述初始条件进行三组仿真,得到的仿真结果如图4~11所示。图4、图7、图10为三种仿真实例得到的飞行器一致性估计器对各自视线角转率估计值与真实值曲线,由图可知各飞行器估计值与真实值曲线几乎完全重合,从局部放大图可以看出,视线角转率的估计误差低于估计精度较高。图5、图8、图10为三种仿真条件下得到的目标加速度估计值与真实值曲线,实线为真实值,各飞行器的估计值能够达到一致并且趋于真实值,在目标加速度不断变化的情况下,各飞行器经过短暂的调整依然能够精确地跟踪真实值曲线,表明本文所设计的一致性估计方法具有较强的鲁棒性。同时观察图3、图9、图12法向加速度指令可知,通过对目标状态的补偿,飞行器状态趋于稳定,表明本文给出的一致性协同估计方法是有效的。
对比三组仿真结果可知:在目标机动能力较小时(仿真实例1),本文设计的一致性估计器估计精度相对较高,加速度估计误差小于0.1 m/s2,收敛速度更快,大约15 s左右收敛。随着目标机动能力的增强(仿真实例2和3),估计器需要调节的时间相应延长,大约20 s左右收敛,加速度计估计误差小于0.5 m/s2仍然能够满足估计精度的要求。
仿真实例1:目标以固定速率做转弯机动
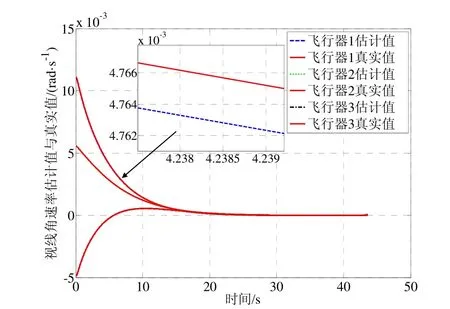
图4 转弯机动时的视线角速率估计值与真实值Fig.4 Estimated and true angular rates of line-of-sight during turn maneuver
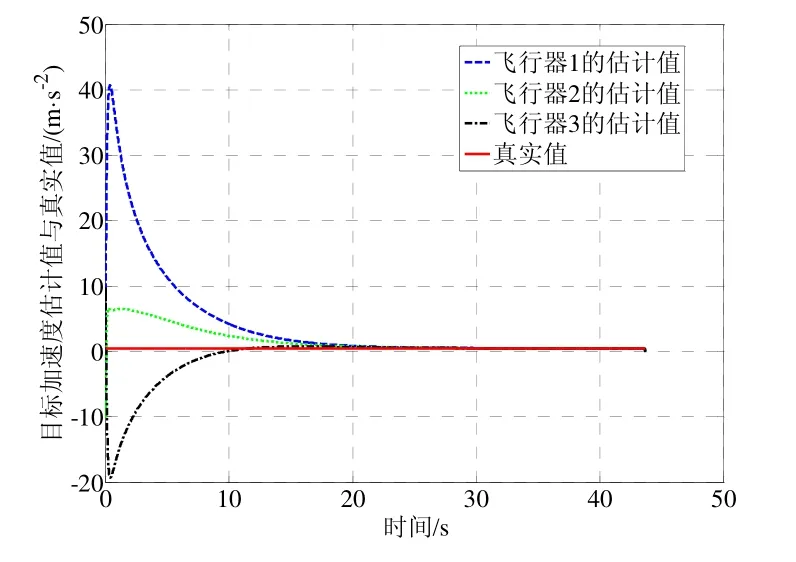
图5 转弯机动时的目标加速度估计值与真实值Fig.5 Estimated and true values of target acceleration during turn maneuver
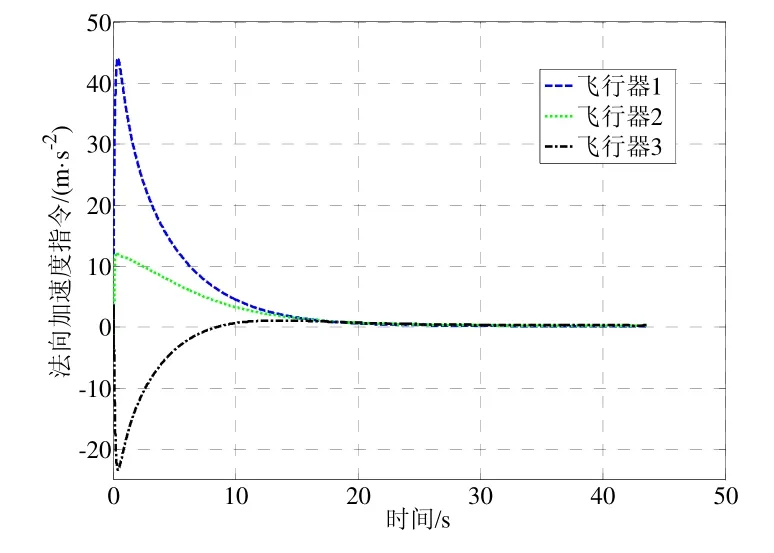
图6 转弯机动时的法向加速度指令Fig.6 Control command perpendicular to line-of-sight during turn maneuver
仿真实例2:目标做蛇形机动
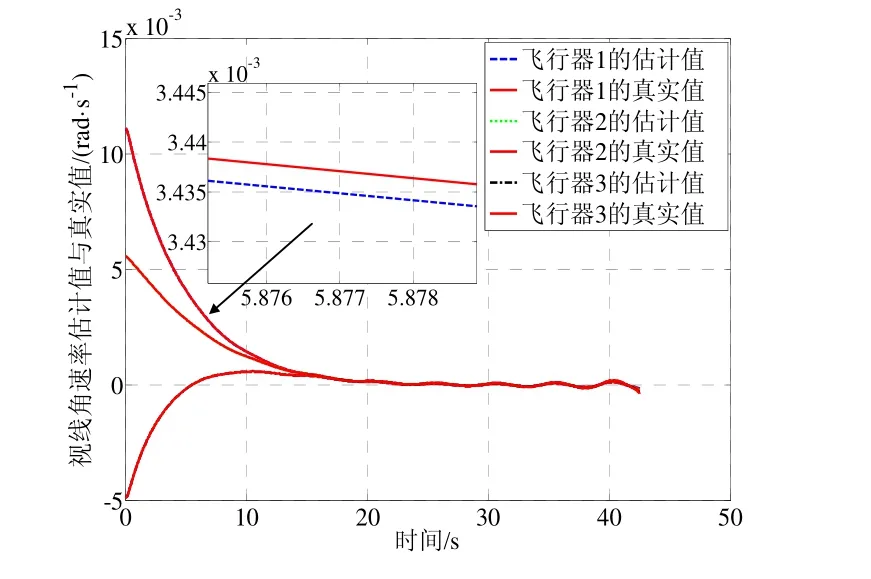
图7 蛇形机动时的视线角速率估计值与真实值Fig.7 Estimated and true angular rates of line-of-sight during snake maneuver
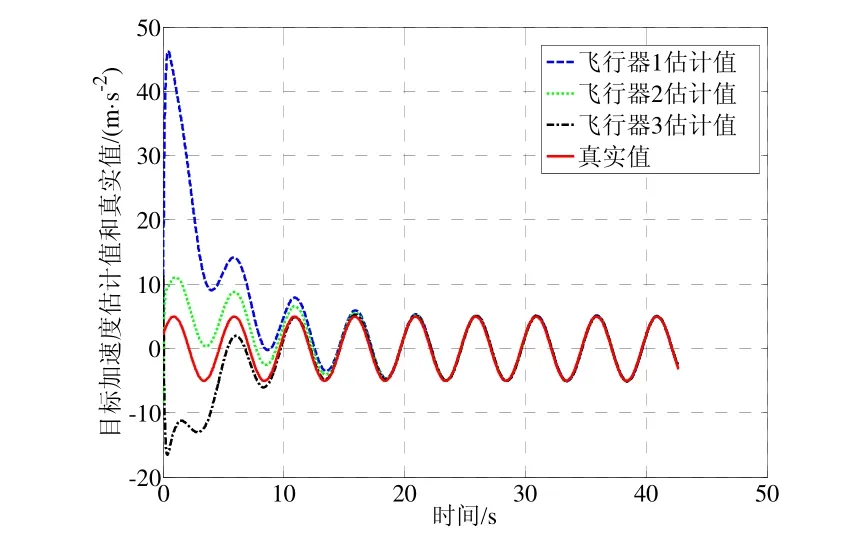
图8 蛇形机动时的目标加速度估计值与真实值Fig.8 Estimated and true values of target acceleration during snake maneuver
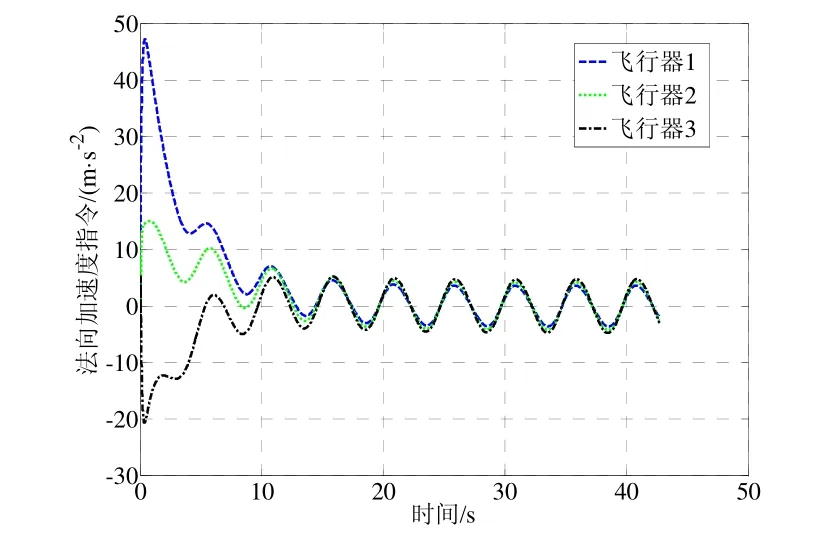
图9 蛇形机动时的法向加速度指令Fig.9 Control command perpendicular to line-of-sight during snake maneuver
仿真实例3:目标进行方波机动
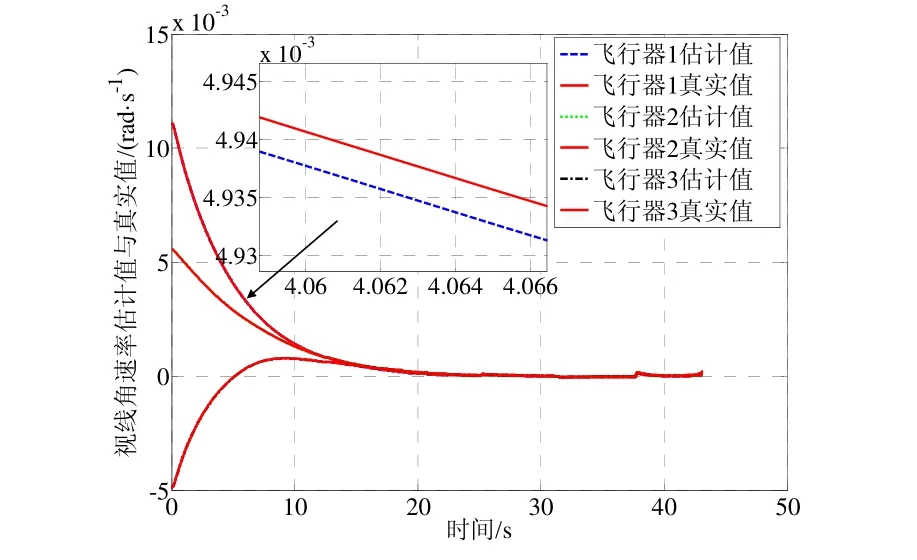
图10 方波机动时的视线角速率估计值与真实值Fig.10 Estimated and true angular rates of line-of-sight during snake maneuver
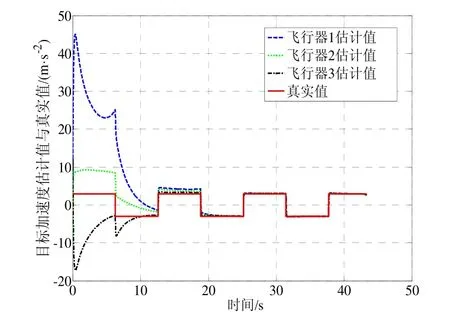
图11 方波机动时的目标加速度估计值与真实值Fig.11 Estimated and true values of target acceleration during square-wave maneuver
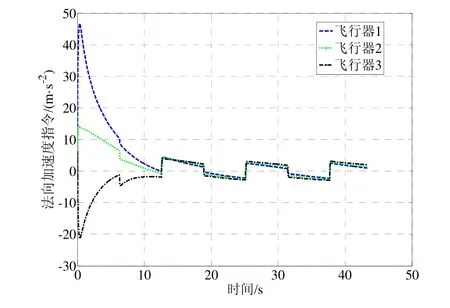
图12 方波机动时的法向加速度指令Fig.12 Control command perpendicular to the line-of-sight during square-wave maneuver
4 结 论
本文提出了一种基于一致性理论的多飞行器协同估计算法。该算法以扩张状态观测器为基础,设计对机动目标的估计方法,通过飞行器间的通信网络交换彼此的估计信息,将一致性协调量引入到各飞行器的状态估计协议中,使通信网络内的飞行器能够给出一致的目标状态估计值,以实现对机动目标状态快速、精确的估计。仿真结果表明,本文设计的一致性协同估计算法精度高,收敛速度快,且在目标进行大机动时仍具有较强的鲁棒性。
参考文献(References):
[1] Jeon I, Lee J. Homing guidance law for cooperative attack of multiple missiles[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(1): 275-280.
[2] Zhou J L, Yang J Y. Distributed guidance law design for cooperative simultaneous attacks with multiple missiles[J].Journal of Guidance, Control, and Dynamics, 2016, 39(10):2436-2444.
[3] Battistelli G, Chisci L. Stability of consensus extended Kalman filter for distributed state estimation[J]. Automatica,2016, 68: 169-178.
[4] Ji H H, Lewis F, Hou Z S, et al. Distributed informationweighted Kalman consensus filter for sensor networks[J].Automatica, 2017, 77: 18-30.
[5] Chai G F, Lin C, Lin Z Y, et al. Single landmark based collaborative multi-agent localization with time-varying range measurements and information sharing[J]. Systems & Control Letters, 2017, 77: 18-30.
[6] Su H S, Chen X, Chen M Z Q, et al. Distributed estimation and control for mobile sensor networks with coupling delays[J]. ISA Transactions, 2016, 64: 141-150.
[7] Guo B Z, Zhao Z L. On the convergence of an extended state observer for nonlinear systems with uncertainty[J].Systems & Control Letters, 2011, 60: 420-430.
[8] Zhu Z, Xu D, Liu J M, et al. Missile guidance law based on extended state observer[J]. IEEE Transaction on Industrial and Electronic, 2013, 60(12): 5882-5891.
[9] Xia Y Q, Pu F, Li S F, et al. Lateral path tracking control of autonomous land vehicle based on ADRC and differrential flatness[J]. IEEE Transaction on Industrial and Electronic, 2016, 63(5): 3091-3099.
[10] Li B, Hu Q L, Ma G F. Extended state observer based robust attitude control of spacecraft with input saturation[J]. Aerospace Science and Technology, 2016, 50: 173-182.
[11] Han J. Active disturbance rejection control technique - the technique for estimating and compensating the uncertainties[M]. Beijing: National Defense Industry Press, 2008.
[12] Zhao E J, Chao T, Wang S Y, et al. Multiple flight vehicles cooperative guidance law based on extended state observer and finite time consensus theory[J]. Proceedings of the Institution of Mechanical Engineers Part G: Journal of Aerospace Engineering, 2018, 232(2): 270-279.

