关注基本图形,玩转45°特殊角

浙江省杭州外国语学校(310023) 袁劲松

1试题呈现

(2017年丽水卷第16题)如图1,在平面直角坐标系xOy中,直线y=−x+m分别交x轴,y轴于A、B两点,已知点C(2,0).

(1)略;(2)设P为线段OB的中点,连结PA,PC,若∠CPA=45°,则m的值是___.

(2017年金华卷第15题)如图2,已知点A(2,3)和点B(0,2),点A在反比例函数的图象上.作射线AB,再将射线AB绕点A按照逆时针方向旋转45°,交反比例函数的图象于点C,则点C的坐标是____.

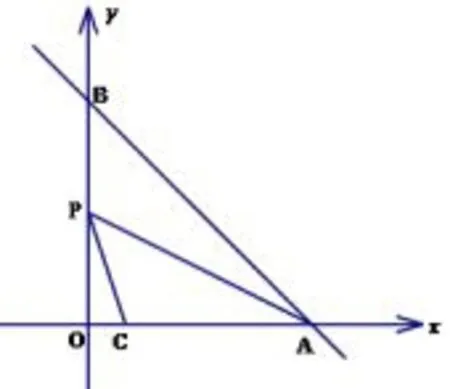
图1

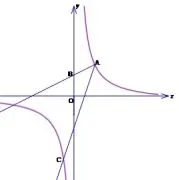
图2

上面的两道中考填空题,虽然形式上不太一样,但是有着一个共同的特点,都存在一个45°的特殊角.因此,如何利用45°的角成为了本题的突破口,45°的角的两边与轴的交点形成了一个类似的三角形,因此这两道题有着如下的共同解法.

2 共同解法展示

2.1 构造“一线三等角”,利用相似三角形

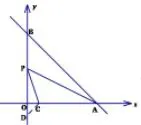
图3

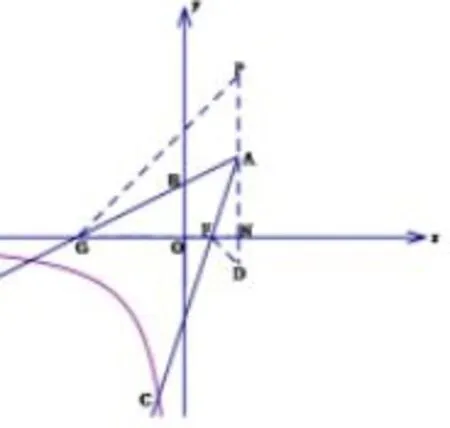
图4

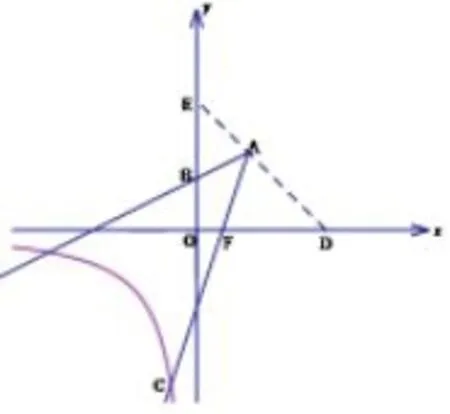
图5

丽水卷解法1如图3,在y轴截取OD=OC,此时∠PDC=45°,可以证得 △ABP∽ △PDC,所以进而得到方程解得m=12.

金华卷解法1如图4,过点A作等腰直角△PNG,作ND=NF,连结DF,易得NP=NG=6,设FN=DN=a,可以证得△APG∽ △FDA,得到得到方程解得a=1,所以F(1,0),求出AF的解析式为y=3x−3,再和联列方程得到C点坐标为(−1,−6).

金华卷解法还可以构造如图5的“一线三等角”模型,构造过点A的等腰直角△ODE,易得DE的解析式为y= −x+5,可得E(0,5)和D(5,0),可以证得△AEB∽ △FDA,所以进而得到方程解得DF=4,得到F(1,0),求出AF的解析式为y=3x−3,再和联列方程得到C点坐标为(−1,−6).

分析“一线三等角”是一种常见的建立三角形相似的方法,该模型在这两小题的应用中看上去有些“异常”,一个只有两等角,另一个根本不存在等角,所以我们利用45°的角去构造等腰直角三角形,形成“一线三等角”的基本模型,再利用相似三角形的基本性质列出方程.

2.2 构造“三垂型”模型,利用全等三角形

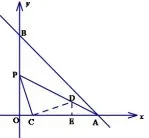
图6

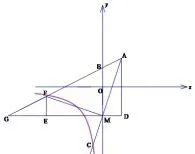
图7

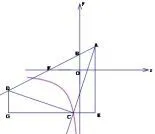
图8

丽水卷解法2如图6,过点C作CD⊥CP交AP于点D,再作DE⊥x轴,易得 △OPC△ECD,所以DE=OC=2,AE=OA−OC−CE=因为DE//OP,所以得到列出方程解得m=12.

金华卷解法2如图7,过点MF⊥AM,构造如图所示的辅助线,易得△EFM=△DMA,设M的坐标为(0,m),可以求出MD=EF=2,AD=EM=3−m,因为点G在直线上,可以求得点G的坐标为(2m−4,m),进而求得GE=1−m,GD=6−2m,因为EF//AD,所以列出方程2:(3−m)=(1−m):(6−2m),解得m=±3(m=3舍去).所以点M的坐标为(0,−3).

金华卷解法如图8,也可以过点C构造如图所示的“三垂型”全等,设点C的坐标为所以CE=DG=2−a,可以求得点D的坐标为又因为点D在直线上,化简得a2−a−2=0,解得a1=−1,a2=2(舍去),所以点C的坐标为(−1,−6).

分析“三垂型”模型是一个基本图形.该模型不仅可以找到全等的三角形,也可以用来证明勾股定理.看到45°角可以构造等腰直角三角形,进而形成“三垂型”模型.

2.3 构造“角平分线”,运用内角平分线的性质

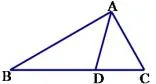
图9

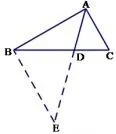
图10

预备知识如图9,AD是△ABC的角平分线,则有

证明如图10,过点B作BE//AC交AC的延长线于点E,可以得到又因为∠E=∠CAD,∠CAD=∠BAD,所以∠E=∠BAD,所以BE=AB,代入上面比例式就可以得到结论.

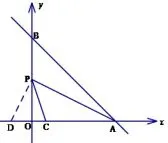
图11

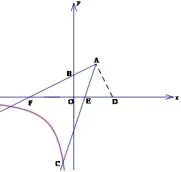
图12

丽水卷解法 3如图11,过点P作PD⊥PA,因为∠APC=45°,所以CP为 △APD的角平分线,因此并且求出D的坐标可以列出方程解得m=12.

金华卷解法3如图12,方法完全同上.

分析由于45°是90°的一半,构造了角平分线,恰好可以利用三角形内角平分线的基本性质.45°这一条件,让人产生了很多遐想,补全直角也是一种常见的手段.

2.4 构造“正方形”,借用正方形旋转

预备知识如图,正方形ABCD,点E,F分别在BC和CD上,且∠EAF=45°,求证:BE+DF=EF.

证明△将ADF绕着点A顺时针旋转90°得到△ABG,可以证得△AEG△AEF,所以EF=EG=BE+BG=BE+DF.

图13

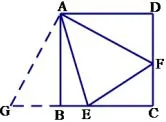
图14

丽水卷解法4如图15,过点P构造正方形OPDE,因为利用预备知识可以得到又因为在△CEN中利用勾股定理得到解得m=12.

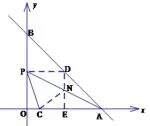
图15

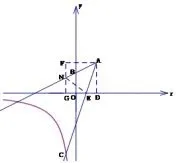
图16

金华卷解法4如图16,因为所以设点E为(m,0),则DE=2−m,GE=1+m.利用预备知识可以得到在直角△HGE中利用勾股定理列出方程解得m=1,得到E(1,0).

分析“半角模型”也是一种常见的基本图形,这类问题一般利用旋转完成,可以得到全等三角形,进而得到线段之间的关系.

2.5 构造“三角形的高”,回到勾股定理

丽水卷解法 5如图17,作CD⊥AP,可知 △PCD为等腰直角三角形.因为PO:AO=CD:AD=1:2,AC=m−2,易得在Rt△POC中,利用勾股定理得解得m=12.

金华卷解法5如图18,作ED⊥AF,(后面计算可得B和D重合),设AD=ED=a,则DE=2a,AF=3a,又因为得到所以所以E(1,0).

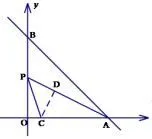
图17

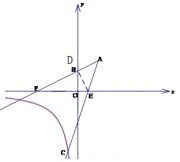
图18

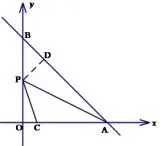
图19

丽水卷解法如图19,我们也可以过点P作PD⊥AB,可得易证△POC∽△ADP,所以得到方程解得m=12.

分析遇到直角问题,有时要回归到勾股定理,利用勾股定理能够列出方程.尤其在折叠问题中,我们经常会利用勾股定理构造方程.本题中依靠∠CPA=45°构造等腰直角三角形,同时得到△POA∽△CDA,一箭双雕.

2.6 构造“四点共圆”,运用两点间的距离公式

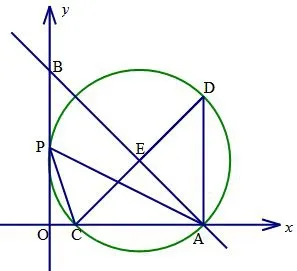
图20

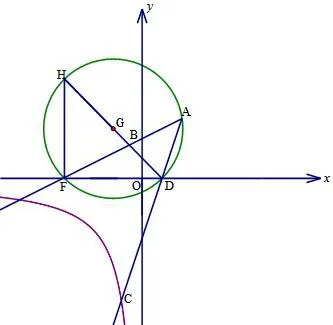
图21

丽水卷解法6如图20,以AC为直角边构造等腰直角 △ADC,因为∠D=∠APC=45°,所以A、C、P、D四点共圆,且以CD为直径,E为圆心.因为D(m,m−2),根据EP=EC,可以列出方程解得m=12.

金华卷解法6如图21,方法同上.

分析“四点共圆”是一种常见的基本图形,它可以运用同弧所对的圆周角相等,半径相等直径所对的圆周角是直角等一系列知识点,灵活多变.

3 解题后的反思

3.1 明确解题方向,确定解题途径

这两道中考题都是以函数为载体的几何问题,以上的解法都充分利用了数形结合,把题中的“形”转化为运算,达到“化形为数”的目的,这是解决问题的关键所在,也是基本思路,有了这些基本思路就有了解决问题的方向.在解决函数中的几何问题时,一定要充分利用几何的基本性质,抓住问题表象中的隐含条件.利用几何性质的同时结合平面直角坐标系的有关计算,达到几何与代数的完美结合.上述解法中的勾股定理和三角形的相似与全等,等腰直角三角形的性质的运用即在意料之外又在情理之中,顺其自然,水到渠成.

3.2 抓住问题本质,学会异中求同

上面的两道中考题看似不同,却有着共同的本质,可以称得上是多题一解.数学问题千变万化,仅仅依靠题海战术是很难抓住数学的本质,盲目地做题还不如静下心来去思考.我们应该由表及里,发现题与题之间的内在联系,抓住问题的本质达到有效的解题.笔者在本文中既有一题多解又有多题一解.一题多解注重学生思维能力的广度,多题一解更善于挖掘学生思维能力的深度,两者并不矛盾并相互依托.因此,在数学解题的教学中,不能只顾其一,要两者兼顾,使得学生的思维即可发散又可回归,做到收放自如.

3.3 活用解题模型,呈现多样解法

基本图形是解决综合性几何问题的一个很好的突破口,从复杂的图形中抽出简单的图形,利用基本图形的性质可以化难为易,让你在解题时由山重水复疑无路突然柳暗花明又一村.数学是思维的科学,因此教师的任务就是要通过教解题,让学生在解题学习中达到“学会思考”这一核心的数学育人功能,教学生解题,应注重在解题的方法,核心概念和基本模型,培养学生加强知识之间的迁移能力.既要注重一题多解,也要关注多题一模型.如何帮助学生识别典型的基本图形结构,怎么进行策略选择,如何完成基本技能的叠加……如果我们能够帮助学生搭建解题的台阶,他们或许在一道题中走得更远,看得更透,离我们期望的能力和素养更近一点.