提取图形几何特征 培养直观想象能力—以求常见多面体外接球球心为例

广东省中山市桂山中学(528463) 邱志权

直观想象是数学核心素养的六大内容之一,它以抽象图形为研究对象,利用几何直观和空间想象来认知和体味事物的形状与性质,借助图形来分析和解决数学问题.主要内涵包括建立形与数的关系、利用几何图形描述问题、借助几何直观理解问题及发挥空间想象能力认识事物.在高中数学教学中,多面体的外接球问题是考察空间直观想象能力的高频考点,因为球与多面体的外接是空间中一种非常特殊的位置关系,而且因为较难画出直观图形而使得问题变得抽象难懂,所以它是一块试金石,全方位、多角度、深层次地考察学生几何直观想象能力.下文从课堂教学出发,立足基础知识和基本技能,以求几类常见多面体外接球的球心方法为例,谈谈数学直观想象能力的培养.

一、以轴定心

球是空间中最具对称性的几何体,当多面体为长方体、正方体、正棱锥、正棱柱、圆锥等具有较明显几何对称特征时,根据直观想象,容易判定外接球的球心一定在多面的“对称轴”上,甚至球心与多面体的“中心”是合一的.

例1 正六棱锥底面边长为侧棱是底面边长的2倍,则它的外接球表面积为___.

解析由定义可知,正六棱锥底面为正六边形,所有侧棱相等,顶点在底面的射影为底面中心.顶点与底面中心的这条连线,它上面的任一点到底面的每一个顶点距离都相等,类比线段的中垂线,我们可以定义它为这个面的“中垂线”;同时这条连线上任一点都可以在侧面上找两个点以它为中心对称,所以我们也可以定义它为该几何体的“中轴线”.它虽然并不是严格意义上的对称轴,但在两个维度方向上与球都具有对称性,所以根据几何直观,球心一定在这条“中轴线”上,最终球心的定位只须满足它到正六棱锥的顶点的距离等于到它底面任某一个顶点即可.

解答如图1,作正六棱锥P−ABCDEF,PO⊥平面ABCDEF,在PO上取点G,当PG=GB时,点G为外接球的球心.3.设PG=BG=R,则在Rt△GBO中:R2=(3−R)2+3,解得:R=2,从而外接球表面积为16π.

图1

由上例可推而广之,所有正棱锥的外接球球心都在它的“中轴线”上,并满足一般性结论:若正棱锥的高为h,底面中心到顶点距为d,则外接球的半径R满足:

拓展若是圆锥的外接球半径,只需将d置换为圆锥底面半径r即可.

二、以形补形

我们知道,正方体、长方体外接球心与长方体、正方体的几何中心是重合的,即外接球的球心为长方体对角线的中点,所以外接球直径等于长方体对角线长.当长方体三边长分别为a,b,c时,则半径(特别的:正方体外接球半径为

例2 三棱锥P−ABC三侧棱两两垂直,PA=5,PB=4,PC=3,求它外接球表面积.

解析三棱锥三侧棱两两垂直,根据几何直观,它具有长方体一个“角”的几何特征.所谓“窥一斑而知全豹”,我们可运用空间想象能力,将这个几何体拓展成一个长方体,也就是说,根据它的几何特征,将它“补形“为一个长方体,问题就化归为长方体外接球的问题,则迎刃而解了.

解答作长方体PAMB−CNRQ,如图2,若PA=5,PB=4,PC=3,则三棱锥P−ABC为题目所给三棱锥,它的外接球直径为长方体对角线长,所以半径外接球表面积:

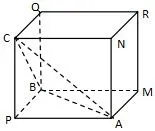
图2

由此可见,同一点出发的三条棱两两垂直,具有长方体局部的几何特征,一般情况下,都可以“以形补形”,将其补成长方体.除此之外,一条侧棱垂直于矩形底面的四棱锥、一条侧棱垂直于直角三角形底面的三棱锥和底面是直角三角形的直三棱柱都可以补形为相应长方体.若推广到更一般的结论:有一条侧棱垂直于底面的棱锥,若存在外接球,则以该棱锥底面为下底面,将它补形为一个直棱柱,直棱柱上下底面的外心(外接圆圆心)连线的中点就是该棱锥的外接球球心.

例3 已知三棱锥则求三棱锥A−BCD外接球的表面积.

解析该三棱锥最明显的几何特征是对棱异面且两两相等,而长方体每个面内的一条对角线在相对面内存在一条对角线与它异面且相等,由几何直觉可知,该三棱锥包含于一个长方体内,反之由该三棱锥可补形为一个长方体.

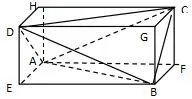
图3

解答作长方体EBFA−DGCH,如图3,设AE=x,AF=y,AH=z,连接AB,BC,CD,DA,DB,AC,则三棱锥A−BCD满足AB=CD,BC=AD,AC=BD,当时则,三式平方相加可求出x2+y2+z2=77,即长方体对角线为因为三棱锥与长方体的外接球为同一球面,所以外接球半径从而外接球的表面积为S=4πR2=77π.

由两道例题可知,当一个几何体的几何特性符合另外一个几何体的局部特征,则可以“以形补形”,将问题化归为另一个更规则的几何体问题,化繁为易.

三、以心追心

所有几何体外接球问题,其核心就是球心的定位,就是要在空间中找到一点,使它到多面体的每一个顶点的距离都相等.一般情况下是不可能“一箭中的”,需要我们先“定圆心”再“定球心”.

例4 在四面体S−ABC中,SA⊥平面ABC,∠BAC=120°,SA=AC=2,AB=1,则求四面体外接球表面积.

解析本题三棱锥底面为非等腰的钝角三角形,无法通过“补形”的办法化归到长方体,只好通过先找底面的外接圆,因为这个外接圆为外接球的一个截面圆,根据球的几何性质,球心一定在过截面圆圆心且垂直于截面的直线上,这样我们就找到第一类问题中所定义的底面ABC的“中垂线”,(其实两者是一致的,都是过底面外心且垂直于底面的直线,当底面为正多边形时,外心就是它的“中心”).

图4

解答如图4,在△ABC中,BC2=AC2+AB2−2AC×则 △ABC外接圆直径设外接圆圆心为O,则作OG⊥平面ABC,当GA=GS时,点G为外接球球心,则所以外接球表面积为

如果类比多边形的外接圆性质:多边形外心为各边中垂线的共同交点,则多面体的外接球的球心为各面的“中垂线”的共同交点.但在空间中找两条直线的交点,一般情况下则不容易解决,除非在特殊的情况下,所以一般都是先到找一个面的截面圆的圆心,也就是先“定圆心”,然后再在过这个圆心的垂线上找一点,使它与底面某顶点和其它顶点的距离相等,就是第二步的“定球心”.

例5 《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马;将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥P−ABC为鳖臑,PA⊥平面ABC,PA=AB=2,AC=4,三棱锥P−ABC的四个顶点都在球O的球面上,则球O的表面积为()

A.8πB.12πC.20πD.24π

解析本题三棱锥每一个面都是直角三角形,斜边中点为其外心,所以找任何一个面的“中垂线”都较简单,甚至两个面的“中垂线”的交点也不难确定.

解答因为PA⊥平面ABC,所以△PAB和△PAC已是为Rt△ ,要△ABC和△PBC也为Rt△ 必须有BC⊥AB且BC⊥PB.

(方法一)如图5:可知底面Rt△ABC的外心为AC中点E,过点E作平面ABC垂线交PC于点O,则点O为PC中点.在Rt△PAC中,因为斜边PC中点O满足OA=OP,所以OP=OA=OB=OC,从而点O为外接球球心.

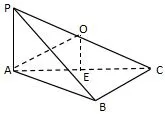
图5

(方法二)如图6:Rt△PBC的外心为PC中点O,Rt△PAC的外心也为PC中点O,这两个三角形的“中垂线”都经过点O,从而点O为两个面的“中垂线”的交点,所以点O为外接球的球心.

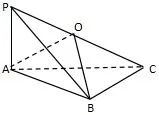
图6

所以外接球半径表面积S=20π,正确选项为C.

四、以数解形

数与形是数学中的两个最古老,也是最基本的研究对象,我们可以利数的严谨性来定义或描述形的几何属性,反之亦可用几何直观来阐释数的关系.球作为三维空间里最基本的几何图形,它的最重要的几何特征是球面上任一点到球心的距离都为定值,若将多面体与其外接球安置于空间直角坐标系下,则空间每一点与空间坐标对应起来,球的几何属性通过数的“表达”,则非常通透明了.

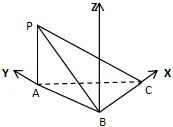
图7

以前面例5为例,以点B为坐标原点,BC、BA所在直线为X、Y轴,以过点B且平行于PA的直线为Z轴,建立如图的空间直角坐标系.则图中各点坐标为:设外接球的方程为:(x−a)2+(y−b)2+(z−c)2=r2,依次代入四点坐标得:,可解出:即外接球球心位置为半径为所求面积S=20π.

培养学生直观想象能力是数学教学的重要目标之一,它可通俗地可表达为要让学生“会想到,能解决”.所以我们在平常教学中,必须立足基础知识、基本技能,注重提取空间几何体的基本属性和几何特性,抓住几何关系的本质和规律,培养学生直观想象能力.