浅谈教学中如何帮助学生构建良好的数学认知结构
广东省广州市绿翠现代实验学校(510300) 唐秋萍
数学教学的本质是:学生在教师的引导下能动地建构数学认知结构,并使自己得到全面发展的过程.数学教学的根本任务就是要造就学生良好的数学认知结构,以满足后继的学习需要,最终提高学生的问题解决能力.在数学教学中如何帮助学生建构良好的数学认知结构,是推进实施有效教学策略所面临的一项重要课题.本文将从以下几个方面来阐述如何帮助学生构建良好的数学认知结构.
一、数学认知结构概念的界定
(一)数学认知结构的含义
数学认知结构就是学生头脑里获得的数学知识结构,只不过是一种经过学生主观改造后的数学知识结构,它是数学知识结构与学生心理结构相互作用的产物,其内容包括数学知识和这些数学知识在头脑里的组织方式与特征.学生的数学认知结构是在后天的学习活动中逐步形成和发展起来的,由于不同主体对知识内容的理解和组织方式不同,所以数学认知结构是有个体差异的.
(二)数学认知结构与数学知识结构的联系与区别
数学认知结构和数学知识结构是两个不同的概念,它们之间既有密切的内在联系,又在严格的区别.两者的联系主要反映为学生的数学认知结构是由教材中的数学知识结构转化而来的,数学知识结构是数学认知结构赖以形成的物质基础和客观依据、两者的区别主要表现在以下几个方面:(1)概念的内涵不同;(2)信息的表达方式不同;(3)结构的构造方式不同;(4)结构的完备性不同;(5)内容的科学性不同.
在强调知识结构与认知结构的区别的同时,并不否认二者之间的密切联系,数学知识结构通过内化在学习者头脑中,形成观念的内容和组织,就构成数学认知结构.所谓内化就是数学知识通过感觉、知觉、记忆、思维、联想等认知活动转化为学生头脑中的数学认知结构的过程.
二、良好的数学认知结构的特征
数学教学的根本任务就是造就学生良好的数学认知结构,以满足后继学习的需要,最终促进学生的全面发展.那么,具备什么特征的数学认知结构才是良好的呢?前人从不同的角度进行了探讨,简述如下:
(一)根据美国教育心理学家奥苏贝尔的观点可知,良好的数学认知结构有以下三个特征:
(1)可利用性,即在学习者原有的数学认知结构中有适当的起同化作用的观念可以利用;
(2)可辨别性,即新知识与学习者原有的数学认知结构中的相关观念是可辨别的;
(3)稳定性,即同化新知识的原有的观念是清晰和稳定的.
(二)华南师大何小亚先生从问题解决出发,认为良好的数学认知结构的特征包括以下四个:
(1)足够多的观念;(2)具备稳定而又灵活的产生式;(3)层次分明的观念网络结构;(4)一定的问题解决策略的观念.
(三)严正香和黄德成老师从实际教学出发,认为学生良好的数学认知结构具有以下特征:
(1)有序性;(2)广阔性;(3)构建性;(4)策略性.
总之,良好的数学认知结构的特征是有利于产生层次更高的数学认知结构.
三、教学中构建良好的认知结构策略
(一)帮助学生构建合理的知识结构,完善学生的认知结构
根据学习的认知理论,数学学习过程是一个数学认知过程,即新的数学学习内容和学生原有的数学认知结构相互作用形成新的数学认知结构的过程.数学学习过程包括三个阶段:新知识输入阶段,新旧知识相互作用阶段和新知识进行操作阶段.奥苏贝尔强调,学生原有的知识结构是决定新的学习的最重要的因素.他指出,“如果我不得不把全部心理学还原为一条原理的话,那么我会说,影响学习的最重要因素是学生已经知道了什么,根据学生原有的知识状况进行教学.”由此可见,教师在向学生输入新的知识时,必须注意学生原有的知识水平和认知水平,换句话说,学生的认知结构中必须具有适当的知识,即合理的知识结构.因此,教师在数学课堂教学中就要帮助学生构建合理的数学知识结构,完善学生的数学认知结构.
(二)帮助学生优化定理教学,构建学生良好的认知结构
数学定理的学习主要是让学生掌握数学概念之间的本质联系,使学生原有数学认知结构中的两个或者多个固定点联系起来,在数学认知结构中形成一个新的固定点,有效的教学方法能使学生在头脑中建立起数学观念之间稳定的联系,从而使学生在头脑中形成关于所学定理的稳定的认知结构,从而完善学生的数学认知结构.
数学定理内化后是数学认知结构的重要组成部分,随着数学学习过程的不断发生,数学认知结构的内部观念在不断地分化和抽象,形成了许多大大小小的“金字塔”结构,这些小“金字塔”结构又互相联系成了一种立体网状结构.每个定理的形成都包含如下两个过程:一是相关的数学观念的形成过程;二是定理观念的形成.
为构建良好的数学认知结构,笔者在数学定理教学中采取如下措施:
(1)形成稳定清晰可辩别的相关数学概念;
(2)引导学生在问题情景中发现数学定理;
(3)让学生掌握最基本的逻辑知识、逻辑规律和逻辑方法;
(4)帮助学生认识理解和掌握定理之间的关系.
(三)重视数学思想方法的渗透,形成良好的认知结构
数学知识结构通过内化形成数学认知结构,而数学思想是数学知识结构的精髓,是数学知识的内核,正是由于数学思想方法的存在,才使得数学知识不再是孤立的单点或离散的片段,使得解决问题的方法不再是刻板的套路和个别的一招一式,因此数学思想方法在数学认知结构中起着固定的作用.聂春霞老师在其《数学认知结构的层次及转化》一文中认为,含有数学思想方法的数学认知结构可称之为高层次的数学认知结构,反之便是低层次的.因此,要想实现数学认知结构由低到高的转化,必须重视数学思想方法的教学.笔者认为至少要从两方面入手:(1)注重数学思想方法的课堂渗透;由于数学思想方法具有隐蔽性强,抽象度高等特征,学生自己概括和总结不易得到,所有教师必须在课堂上有意识的渗透其载体及数学认知结构中已有的思想方法建立联系.课堂中渗透数学思想方法有下面措施:是在知识的发生过程中渗透数学思想和数学方法;是在在解决数学问题中渗透数学思想方法;是化隐为显,揭示数学思想方法.(2)注重数学思想方法的及时加强;数学思想方法是高度抽象化的,仅凭学生在课堂上的学习和理解是不够的.隐私做相应的练习必不可少.由于数学思想方法蕴含在多个分支中,所以综合性问题与实际问题的解决对巩固数学思想方法会更加有效.
总之,想让学生将数学思想方法应用自如,需学生在解题实践中反复练习和运用,使数学思想方法转化为自己的“经验”和“习惯”,这样才能让学生形成对数学思想方法有良好认知结构.
(四)充分暴露数学思维过程,调动学生思维的积极性
数学教学活动中存在着三种思维活动,即数学家的思维活动,数学教师的思维活动和学生的思维活动.在数学教学中,暴露数学思维过程,就是重视数学知识产生的思维过程.教师既要暴露数学家的思维活动,又要暴露教师的思维活动,还要让学生暴露他们自己的思维过程.这样才能使知识的逻辑展开与学生的认知规律相结合,让学生参与知识的形成过程,弄清知识的来龙去脉,在“揭露”的过程中优化学生的数学认知结构,调动学生思维的积极性.那么在教学过程中应该如何暴露学生的思维过程呢?笔者认为需要做到以下两点:一是教师必须让学生正真参与到知识的探索中去,不能以教师的教去代替学生的学;二是教师必须尊重学生的思维选择,尽量沿着学生的思维轨道,对思维展开调控.
(五)帮助学生构建数学知识网络,培养学生系统的思维导图
知识网络构建是指学生把所学知识与多方面的相关知识进行串联,建构起新知识与各方面因素间的网络构架.但同时教师对其要有透彻的认识,才能帮助学生不仅在形式上建立如概念图的知识网络结构,而且使其结构中的信息流通畅顺,即结构中各知识点之间有着其数学本质意义的联系.
例如:学完“数列”一章概念即可帮助学生构建如下知识网络图:
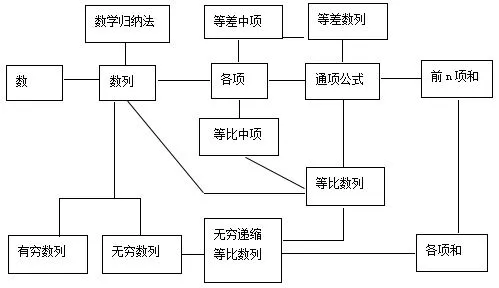
通过这个知识网络,对数列这章的所有定理和公式都能清楚的梳理,也能从系统的看数列知识的考点和联系.所以教师应该帮助学生主动地对所学的知识进行分类和归纳、整理和提炼,构建出适合自己的知识网络,以便在解决数学问题时更快地提取有关知识点,达到提高问题解决的能力.
(六)培养学生良好的反思习惯,巩固学生的认知结构
在数学学习过程中,良好的反思习惯有助于学生构建数学认知结构.所谓反思,就是学习者对自身数学学习活动的过程,以及活动过程中涉及的有关事物的学习特征的反向思考.笔者认为学生对知识的反思分为两种:一是总结性反思,即考虑解题的关键步骤用到了哪些定理、法则、体现了什么思想方法.对解题中出现的挫折要找出原因,弄清哪部分知识不熟悉造成,这样从正反两个方面强化了所学知识,提高了数学思维能力;二是提高性反思,即对所解的数学问题进行发散性扩展或是收效性概括.发散性扩展,指通过改变习题条件,扩大外延的一题多变的思考,培养发散性思维;收敛性概括,是对所解的题目从结构上和思路上进行抽象、概括和归纳,以便形成高层次的题型模式和数学思维模式.
总之,反思学习是智能发展的高层次表现,是建构学说在教学实践中的主要体现.唯有反思,才能控制思维操作,才能促进理解,提高学生的认知结构水平,从而促进教学观点的形成和发展,不断完善学生的认知结构,实现良好的循环.
[1]何小亚.建立良好的数学认知结构的教学策略[J].数学教育学报,2002,11(1):24-27.
[2]严正香、黄德成.如何建构学生良好的数学认知结构[J].沈阳农业大学学报(社会科学版),2005,7(2):190-191.
[3]涂荣豹.试论反思性数学学习[M].数学教育学报,2000,(4).
[4]管鹏.形成良好数学认知结构的认知心理学原则[J].教育理论与实践,1998,18(2):40-45.

