提升数学问题解决能力,重视基本方法教学
龙岩初级中学(364000) 王斌
提高学生数学解题的能力是数学老师重要的教学工作,在教学中如何提高学生解题能力上,很多老师想到的是,培养学生的整体思想、模型思想、化归思想、分类思想等数学思想.往往忘记(或者没有想到),了解掌握一般数学问题解决的基本方法是学生提高解题能力的重要抓手,是学生灵活地、综合地运用数学思想进行解题的根本,更是让我们的解题教学成有源之水.如何让学生掌握一般数学问题解决的基本方法的方法呢?笔者认为教师可以做好以下几个方面.
一、明确基本方法,让学生了解一般数学问题解决的基本方法.
解决数学问题是数学老师的基本能力和基本功,但我们发现有的数学老师自己很会做题,但讲解时,学生还是很难听懂或者听完后往往一知半解,观其教学,平时讲题往往是这样的:已知“什么”,可以得到什么,进而得到什么;或者是:要得到这个结论,那么需要什么条件;要不就两者简单地结合.对于一般数学问题解决过程的基本方法渗透做得很少,甚至没有.进一步了解,许多数学老师对一般数学问题解决过程的基本方法都不清楚,讲题仅仅凭经验.所以笔者认为,作为一名数学老师掌握好一般数学问题解决过程的基本方法是一个基本要求.对于一般数学问题解决过程许多数学家都有阐述过,虽然各种阐述有所区别,但是大体是相似的.接下来我们看看美国数学教育家A·沙思菲尔德(A·Schoenfeld)对一般数学问题解决过程的阐述:(1)了解问题,(2)尝试理解整个问题,(3)试探一些思路,(4)寻找新信息和局部评价;(5)实施计划;(6)证实;(7)以上各个阶段之间的联络和转变.对于初中学生来说也许并不能对这样的阐述有很好的理解,但老师可以在这样阐述的基础上,用学生可以理解的语言来表述.如:(1)我们要解决的是什么问题(问题中有什么已知条件和未知条件),(2)解决问题有什么思路或都有什么经验可用,(3)由条件可得出哪些结论,(4)这些结论哪些对问题解决可能有用,(5)用已知的条件和得到的结论组合尝试进一步解决问题(推理),(6)写出解题(或证明)过程.
二、暴露思维过程,让学生体验一般数学问题解决的方法.
同样的题目,同样的解题过程,不同老师的讲解,对学生获得的知识,思维的启发,解题能力的提高就有很大的差距,这就与老师在讲题的时候是否善于暴露问题解决的思维过程,是否在这一过程中渗透解题的一般方法,是否促进了学生会思考,能探索,是否让学生在这一过程中体验到数学解题的逻辑性、严密性、发展性、巧妙性等进而激发解题的参与性和积极性有很大的关系.下面以一道简单的几何证明题为例,通过暴露思维过程的方法,让学生体验一般数学问题解决的方法.
例如图1,F,G是OA上的两点,M,N是OB上的两点,且FG=MN,△PFG的面积和△PMN的面积相等,求证:OP平分∠AOB.
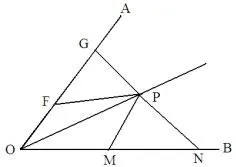
图1
提问(1)我们从哪里开始?从题目的叙述开始,我们要解决的是什么问题,有那些条件,那些结论;条件:FG=MN、△PFG的面积和△PMN的面积相等,结论:OP平分∠AOB
(2)我能做什么?说到两个三角形面积相等,我们可以想到小学学过的三角形的面积公式:底乘以高除以二,FG、MN分别是△PFG、△PMN的边,再由FG=MN我们可以想到FG边上的高和MN边上的高相等,如图2,分别画出两条高PE、PH,则有PE=PH.

图2
(3)要解决的问题:证明OP平分∠AOB,证明射线为一个角的平分线,我们学习了什么方法(思路与经验):证射线分成的两个角相等(如图,证∠AOP=∠BOP)证射线上的点到角两边的距离相等(角平分线的判定);
(4)前面得到的结论对问题解决可能有用吗?我们前面得到的结论是两条高相等即PE⊥OB,PH⊥OA且PE=PH.
(5)用已知的条件:△PFG的面积和△PMN的面积相等,得到结论:点P到角的两边距离相等,满足角平分线判定的条件这样问题就可以解决了.
(6)从已知出发,让我们尝试写出证明过程.
数学老师在解题教学中,要经常有意识地用一般数学问题解决的方法暴露解题的思维过程,让学生在学习用基本方法解决数学问题中感受到水到渠成的体验,学生就会逐步地运用并掌握一般数学问题解决的方法.
三、通过变式拓展,让学生熟练运用一般数学问题解决的方法
人们对事物的认知都有个循序渐进的过程,对数学问题解决方法的理解与能力的提高也是一个从感知、了解、理解、掌握与运用的过程.学生对一般数学问题解决的有了一定的了解后,为了促进学生进一步理解与掌握一般数学问题解决的方法,我们可以在恰当的时机,(学生学习了两个或两以上相类似的题型后或者在期中、期末、中考复习),以试题为源头,以模型为基础,通过变式来巩固,通过拓展来提升的方式,让学生获取解题通法,掌握解题技巧,从而熟练运用一般数学问题解决的方法
试题十边形有几条对角线?
分析什么是多边形的对角线(连接多边形不相邻的两个顶点的线段),能画出十边形全部的对角线吗?(很难).
模型我们有画过五边形的对角线吗?(有过),怎样画比较不会遗漏呢?(从第一个点出发,画出所有对角线;再从第二个点出发,画出所有对角线,依次类推从第三个点、第四个点、第五个点出发画出所有对角线),从第一个点出发可以画对角线可以画多少条?(5−3=2),每个顶点都可以画2条,但这样每一条对线都会重复画一次,所以,共有对角线(5−3)×5÷2=5条.
解决问题 画十边形的对角线与画五边形的对角线相类似,每个点出发除了自己本身和两个相邻的两个顶点与(10−3)个点可以连成对角线,共有对角线(10−3)×10÷2=35条.
变式n边形有几条对角线?(每个点出发可以画(n−3)条对角线,有n个点且每条对角线都会重复算一次,所以共有条对角线.)
拓展
1、直线上有n个点,以这些点为端点的线段有几条?
2、锐角内部有n条以锐角的顶点为端点的射线,则图形中共有几个角?
3、n条直线两两相交,最多有几个交点?
4、班上有n个同学,每个同学都要和其他同学握手一次,全班共握手几次?
归纳提升以上的问题都是一组对象中有n个元素,每个元素与其他元素联系得到结果,且每个元素与其它的元素的联系得到结果的个数(m)是一样的.那么总的结果数是
通过恰当的变式、拓展训练能提高学生发现数学问题本质(问题中有什么,要做什么)与解决问题(经验与知识迁移、探究与推理)的能力.
数学问题的解决是数学活动的根本与目的,它需要数学知识积累,更需要掌握一般数学问题解决的基本方法,让学生在数学问题的解决过程中,养成观察、猜想、归纳的数学习惯,使学生在“数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析”的数学核心素养中有较大提高.
[1]G·波利亚,怎样解题――数学思维的新方法[M],上海:上海世纪出版股份有限公司出版发行.
[2]王斌,在数学试题探究中提炼模型获取通法[J],福建基础教育研究:初中版2016(5).

