van’t Hoff方程及相关问题的讨论

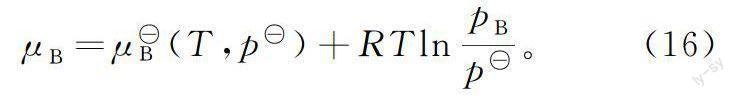
摘要：vant Hoff 方程是描述化学平衡常数与温度之间关系的方程，且有“化学反应等压方程”和“化学反应等容方程”之说。目前教材对于这些方程的推导不严格，甚至不正确，对于“等压”和“等容”的含义也没有解释，造成了该方程使用上存在困难，出现许多错误的结论，使得在推导活化能与反应热关系时出现混乱。针对此问题，从化学势是状态函数入手，证明了摩尔反应吉布斯函数也是状态函数，并以此为基础，利用严谨的数学和热力学概念，推出了vant Hoff 方程。结果表明，vant Hoff 方程的2种形式，即所谓的“化学反应等压方程”和“化学反应等容方程”，其使用条件与等压和等容无关，只是一种习惯叫法而已。在此基础上，严格导出了理想气体化学反应的Arrhenius活化能和恒压反应热及恒容反应热之间的关系。研究明确了任意反应和理想气体反应van Hoff方程的形式和使用条件，对人们正确认识和利用热力学领域理想气体反应活化能和反应热的关系打下了基础。

关键词：化学热力学；vant Hoff 方程；恒压反应；恒容反应；理想气体；活化能

中图分类号：O642文献标志码：Adoi： 10.7535/hbgykj.2018yx01004

Discussion on vant Hoff equation and related problems

REN Jujie

（School of Science， Hebei University of Science and Technology， Shijiazhuang， Hebei 050018， China）

Abstract：vant Hoff equation is the equation describing the relationship between chemical equilibrium constant and temperature， and there is the equation socalled "chemical reaction isobaric equation" and "chemical reaction isochoric equation". In the current textbooks， the derivation of these equations is not strict， even incorrect， and there is no explanation for the meaning of "equal pressure" and "equal capacity". This makes difficulties in the use of the equation， resulting in many wrong conclusions， and leads to confusion in the derivation of the relationship between activation energy and reaction heat. Starting from the state function of the chemical potential， it is proved that the molar reaction Gibbs function is also a state function. Based on this， the vant Hoff equation is introduced using rigorous mathematical and thermodynamic concept. It is also proved that the two forms of the vant Hoff equation， the socalled "chemical reaction isobaric equations" and "chemical isometric equations"， are not related to isobaric and isometric. It's just a habit name. On this basis， the relationship between Arrhenius activation energy and constant pressure reaction heat and constant volume reaction heat of the ideal gas chemical reaction is strictly derived. This study clarifies the vant Hoff equation and the use conditions of the equation of arbitrary and perfect gas reactions， and lays the foundation for the correct realization and application of the relationship between perfect gas reaction activation energy and the reaction heat in the thermodynamics field.

Keywords：chemical thermodynamics； vant Hoff equation； isobaric reaction； isochoric reaction； perfect gas； activation energy

在大多數物理化学教材中，当讲到温度对于化学平衡常数的影响时一般都会介绍vant Hoff 方程[19]，其中有的教材还提到了vant Hoff等压方程和vant Hoff等容方程等说法，但对于这些方程的使用条件以及等压和等容的含义大部分教材中并没有最基本的说明，有的教材虽然有所说明但也没有说清楚[23]，造成理解和使用上的混乱，给后续该方程的应用带来困难。

例如，文献＼[1＼]是在讨论理想气体反应时引入如下的vant Hoff 方程的：

并且把方程（1）称为vant Hoff 等压方程，把方程（2）称为vant Hoff等容方程，但并没有说明等压和等容的含义。文献＼[2＼]—文献＼[7＼]没有把vant Hoff 方程只限于理想气体反应，而是作为一般论指出，对于任何化学反应，其标准平衡常数和温度间都有如下形式的vant Hoff 方程，

其中，文献＼[2—3＼]还将上式左边仍然写成偏微分的形式

强调左边求偏导的条件是恒压条件，然而这个压力没有写成标准压力。从该文后面的讨论可知，这个压力应该是标准压力。因为上式是由

推导而来，而式（5）的热力学函数是标准态下的热力学函数，标准态的压力就是标准压力，因此式（5）可以去掉外界而成为

将ΔrGm=-RTln K代入式（6）可以推得式（4），因此式（4）的外界是没有必要的。而不是像文献＼[2＼]中说的那样，应用到理想气体才可以去掉下标。文献＼[2＼]之所以这么认为，也是由于其对于vant Hoff 方程的推导过程不清楚造成的。

文献＼[4＼]更是对这个压力外界不知所从，先是得到了式（3）那样的式子，可是在推导气相反应的关系式时又加上了压力下标，后来又不加解释地去掉了。

文献＼[5＼]在讨论活化能与反应热的关系时，对于任意反应，引入如下形式的vant Hoff 方程：

并由此得到了活化能与反应热的关系为

但其没有对方程（7）进行推导，也没有对其使用条件进行说明，且方程的左边和右边都没有标准态的标志，这一切都让人觉得摸不着头脑。而更多的教材中，认为活化能与反应热的关系为Ea，+1-Ea，-1=ΔHm[1011]。

文献＼[6＼]在其下册关于过渡态理论的讨论中指出，“根据平衡常数与温度的关系式：

这样的表达意味着将过程特别限制为恒容过程。文献＼[8＼]更是直截了当地指出所谓的化学反应等容方程d ln Kc/dT=ΔrUm/RT2就只适用于等容化学反应。然而，通过笔者接下来的讨论可知，这种认识是错误的。

由此可见，关于vant Hoff 方程的形式和使用条件非常混乱，并由此导致了活化能和反应热关系的混乱。下面将通过具体推导，弄清任意反应和理想气体反应vant Hoff 方程的形式和使用条件，对某些错误进行说明，对理想气体反应活化能和反应热的关系进行讨论。

1恒压和恒容反应的方向和平衡判据

对于任意化学反应0=∑BνBB系统，在恒温恒压不做非体积功的条件下，从某种状态（T，p，ξ ）再向前进行dξ时，由多组分系统的热力学基本关系式可知，系统吉布斯函数的变化为dG=∑BνBμBdξ，所以，

应当注意的是，不管是在（T，p，ξ ）这种状态还是（T， p， ξ+dξ）这种状态，系统（如反应釜）中反应物和产物都是共同存在的，由于化学势是状态函数，而∑BνBμB是反应系统处于（T， p， ξ ）这个状态时系统中各物质的化学势（亦即偏摩尔吉布斯函数）乘以其计量系数的代数和，因此∑BνBμB也是状态函数，这就像系统的状态函数U加上系统的状态函数pV仍然还是一个状态函数一样。传统上将∑BνBμB记为ΔrGm，它也等于系统状态不变时，比如无限大的系统中，发生1 mol反应时，系统状态函

由以上推导过程可知，认为任意化学反应在恒容条下存在如下关系式：d ln Kc（T，p）/dT=ΔrUm（T，p）/RT2的观点是错误的。无论恒容还是恒压，式（14）都成立。只不过对于溶液反应，ΔrHm（T，p）与ΔrUm（T，p）通常相差不大，而组分的标准态选（T，p，c）时，近似有

3理想气体的2种标准态

对于某状态的理想气体B，不管其处于何种过程，总有

严格地，μB（T，p）是温度为T、压力为p的理想气体B的化学势。对应的状态即“温度为T、压力为p的纯B”是气体B常用的标准态的定义。将

显然，μB（T，c）是温度为T、浓度c=1 mol/dm3、压力pB=cRT的理想气体B的化学势。对应的状态即“温度为T、浓度为c=1 mol/dm3的理想气体B”有时也看作是理想气体B的另一种标准态[6]，注意这种标准态的压力不是p，且是可变的。虽然这个标准态的压力没有规定，但因为规定了浓度，使得温度一定时，压力也一定。由式（18）可以看出，温度一定时，这个状态的化学势μB（T，c）有定值。

有作者认为这个标准态是“温度为T、浓度为c=1 mol/dm3、压力为p的理想气体B”[14]，但由以上讨论可知，这种认识显然是不正确的；并且，如果真是这样，这个标准态的温度就是不可变的了。

尽管理想气体的化学势既可以用式（16）表示，也可以用式（17）表示，但对于某状态的理想气体，不管其处于何种过程，也不管用哪种标准态，其化学势是一定的。

4理想气体反应的平衡常数

在本文的第1部分已经述及，不管是恒压还是恒容条件下的化学反应，其方向和平衡判据都是∑BνBμB=ΔrGm≤0，这一点对于理想气体反应当然也适用。

对于理想气体化学反应，当化学势用式（16）表示时，有

特别值得注意的是ΔrGm（T，p）的物理意义正如它的定义式所表达的那样，是各物質都处在标准态时的化学势与其反应计量系数乘积的代数和，不具有“整个反应系统处在标准压力下”这样的意义。因为如果参与反应的物质（反应物和产物）有不止一种气态物质时，整个反应系统的总压为标准压力时并不能保证每一个参与反应的物质“反应物或生成物”都处在标准状态下，即使是无限大的系统也不行。当然可以创造条件使得各物质都处于标准状态下来进行反应，例如将反应安排成电池反应，但即使这样，也不能使整个反应系统（总压）处于标准压力下，而是使各个物质处在标准压力下。当反应达到平衡时ΔrGm=0，

此式也是理想气体反应以浓度表示的标准平衡常数Kc的定义式。

也就是说，对于一定温度下理想气体间的反应，不管是恒压过程还是恒容过程，其平衡常数既可以用压力表示也可以用浓度表示，并且，用压力表示的平衡常数都相同，即都为式（21），用浓度表示的平衡常数也相同，即都为式（24）。

5理想气体反应的vant Hoff 方程

对于理想气体间的反应，当各组分选用（T，p）的理想气体作为标准态时式（14）适用。但是，对于理想气体间的反应（也只有理想气体间的反应），各组分还可以选用（T，c）的理想气体作为标准态，这时，

形式的Gibbs Helmholtz方程就不能用于此标准态下的物质。因为这样的标准态的压力随着温度的变化而变化，因此式（14）不能适用。这时平衡常数和化学反应热力学函数间的关系可用如下方法获得。

对于以（T，c）为标准态的理想气体B，如果维持标准态，当温度发生变化时，为了维持其浓度为c，体积应不变，压力要发生变化，则有

由推导过程可知，该式也和反应过程无关，即不管是恒容理想气体反应还是恒压理想气体反应，只要各物质都选用（T，c）标准态，则式（30）都成立。

对于理想气体间的化学反应0=∑BνBB，因为kp=（p）-∑νBKp，Kc=（c）-∑νBKc，而（p）-∑νB和（c）-∑νB是与温度无关的常数，所以式（15）和式（30）可写为

由上述推导过程可知，式（31）和式（32）既适用于恒压也适用于恒容下的理想气体反应，这就是严格意义的理想气体化学反应的vant Hoff 方程。一些教課书将式（31）和式（32）分别称为化学反应等压方程和等容方程，显然是不合适的。因为式（31）和式（32）只和选用的标准态有关，和过程无关。

长期以来，教科书和研究者都没有像本文那样对任意反应和理想气体反应的vant Hoff 方程从最基本的概念出发进行详细严格正确的推导，大多数物理化学教科书中，只是对其泛泛介绍，并且多不严格。在这些不严格概念的影响下，对于理想气体反应，某些文献甚至得出了用状态函数法很容易证明是错误的如下结果[1213]：

6理想气体反应Arrhenius活化能与反应热的关系

在传统的物理化学教科书中，在化学动力学一章，为了便于表示反应速率，一般强调过程是恒容过程，而反应物的浓度则多以物质的量浓度表示。

设有如下理想气体化学反应，

正逆反应为基元反应，其中kc，+1和kc，-1是正反应和逆反应速率常数，即v+=kc，+1cEcF，v-=kc，-1cH。反应达平衡时v+=v-，即kc，+1ceqEceqF=kc，-1ceqH，则

由Arrhenius方程（也是活化能的定义式）可得：

d ln kc，+1dT=Ea，+1RT2，d ln kc，-1dT=Ea，-1RT2。

结合推导出的式（32）可知，

参考文献/References：

[1]朱志昂， 阮文娟. 近代物理化学[M].4版.北京： 科学出版社， 2008： 29.

[2]孙世刚， 陈良坦， 李海燕，等. 物理化学[M]. 厦门： 厦门大学出版社， 2008： 389392.

[3]杨永华， 杨桦， 吴凤清，等. 物理化学[M]. 北京： 高等教育出版社， 2012： 337.

[4]陈六平， 童叶翔. 物理化学[M]. 北京： 科学出版社， 2011： 154155.

[5]天津大学物理化学教研室.物理化学[M].5版.北京： 高等教育出版社，2009： 207208.

[6]傅献彩， 沈文霞， 姚天扬，等. 物理化学（下册）[M].5版.北京： 高等教育出版社， 2006.

[7]ATKINS P， de PAULA J. Physical Chemistry[M]. 9th ed. New York： W. H. Freeman and Company， 2010： 223.

[8]周鲁. 物理化学教程[M]. 北京： 科学出版社， 2002： 104105.

[9]郭子成，罗青枝，任聚杰. 物理化学（上册）[M]. 北京：化学工业出版社，2013.

[10]刘幸平. 物理化学[M]. 北京： 中国中医药出版社， 2012： 173174.

[11]郭汉杰. 冶金物理化学教程[M]. 北京： 冶金工业出版社， 2006： 217218.

[12]郭子成， 任杰. 关于-RT ln Kc=ΔrGm（c）的讨论[J].化学通报， 2010， 73（1）：9396.

GUO Zicheng， REN Jie. A discussion on -RT ln Kc=ΔrGm（c）[J]. Chemistry，2010， 73（1）： 9396.

[13]郭子成，任杰，任聚杰.理想气体反应不同标准态时热力学函数间关系式的补充[J].河北工业科技，2011，28（6）：347350.

GUO Zicheng，REN Jie，REN Jujie. Relationships of thermodynamic fuctions of chemical reactions in perfect gases at different standard states：A complementary discussion[J].Hebei Journal of Industrial Science and Technology， 2011，28（6）：347350.

[14]张志红， 赵秀峰. 等压和等容条件下的化学平衡原理[J].昌吉学院学报， 2012 （4）： 8185.

ZHANG Zhihong， ZHAO Xiufeng. The principle of chemical equilibrium under isobaric and constant volume conditions[J]. Journal of Changji University， 2012（4）： 8185.