等面积异形柱与矩形柱多层框架的结构性能对比分析

吴珠峰 曹平周 刘成 伍凯

摘要：为研究当框架柱截面面积相等时，采用异形柱和矩形柱对结构性能的影响，结合某6层框架住宅建筑，在保证同一位置处的异形柱与矩形柱截面面积相等的条件下，运用结构设计软件SATWE分别进行矩形柱框架和异形柱框架的结构设计，对这2种结构进行了地震作用下的层间位移角、楼层最大位移、楼层剪力、剪重比以及结构自振周期、振型等抗震性能的对比分析；根据规范选取了3条地震波，分别运用SATWE和EPDA软件对这2种结构进行弹性和弹塑性时程分析；从钢筋用量的角度进行了经济性的对比分析。结果表明，当框架柱截面面积相等时，和矩形柱框架相比，异形柱框架的抗震性能较好，但经济性稍差一些。研究结果为不同条件下异形柱与矩形柱的选用提供了理论参考。

关键词：混凝土与钢筋混凝土结构；多层框架；异形柱；矩形柱；抗震性能；时程分析；经济性

中图分类号：TU375文献标志码：Adoi： 10.7535/hbgykj.2018yx01005

Contrast analysis on structure performance of multistory frames with equalarea special shaped columns or rectangular columns

WU Zhufeng1， CAO Pingzhou1， LIU Cheng2， WU Kai1

（1. College of Civil and Transportation Engineering， Hohai University， Nanjing， Jiangsu 210098， China； 2. Architectural Design and Research Institute of Tongji University， Shanghai 200092， China）

Abstract： In order to study the effect of using specialshaped column and rectangular column on the structure performance under the condition of equal cross section area of columns， combined with a six layer frame residential buildings， the structure design software SATWE is used for the structure design of specialshaped column frame structure and rectangular columns frame structure. In the two kinds of structure， section area of both specialshaped column and rectangular column in the same location is equal. The seismic performances of the two kinds of structures under seismic load are analyzed， such as interlayer displacement angle， floor maximum displacement， floor shear， shearweight ratio， natural vibration period， vibration mode， etc. According to the specification， three seismic waves are chosen for elastic and elasticplastic time history analysis of the two kinds of structure respectively using software SATWE and EPDA. The economy is also analyzed from the perspective of the amount of reinforcement steel bar. Analysis results show that when section area of frame column is equal， specialshaped column frame structure has better seismic performance than rectangular columns frame structure， but the economy is a bit poor. The study results provide theoretical reference for the specialshaped column and rectangular column selection under different conditions.

Keywords：concrete and reinforced concrete structure； multistory frame； specialshaped column； rectangular column； seismic performance； timehistory analysis； economy

混凝土柱一般設计为矩形截面，当把传统框架中的角柱、边柱、中柱分别替换为“L”字形、“T”字形、“十”字形等异形截面的混凝土柱时，就构成了一个异形柱框架[1]。与传统框架相比，采用异形柱框架时房间四周墙面上没有突出的柱子，这不但增加了室内使用面积，而且也使得室内空间更加规整平滑。一般来说，异形柱各肢最小截面宽度小于300 mm，各肢的肢高与肢厚之比不应大于4[2]，而且肢厚不应小于200 mm，肢高不应小于500 mm。

1工程概况

当地震设防烈度为7度且设计基本加速度为01g时，异形柱框架结构的房屋最大高度不能超过21 m。本文基于江苏南京某6层住宅建筑（层高为3 m），分别进行异形柱框架和矩形柱框架的结构设计。两种结构方案之间除了柱子不一样，其他方面的结构布置都相同。在保证同一位置处的异形柱与矩形柱截面面积相等的条件下，多次运用结构设计软件SATWE进行试算。在确保位移比、层间位移角、周期比、层间刚度比、层间受剪承载力比、剪重比、刚重比、轴压比、构件是否超筋等各个方面都满足现行规范要求的情况下，通过不断地调整、优化并最终确定出相应的结构布置方案[38]。最后设计出的矩形柱框架和异形柱框架的结构布置方案分别如图1和图2所示。

2结构抗震性能对比

2.1层间位移角

层间位移角是楼层层间最大水平位移与层高的比值，是检验建筑结构抗震性能的主要指标之一[910]。对层间位移角进行控制的主要目的是为了使建筑结构具备足够的侧向刚度，对结构构件的刚度大小、截面尺寸大小起到一定的控制作用，避免建筑结构在水平荷载作用下产生过大的水平位移，以满足结构对承载能力、稳定性等承载能力极限状态和舒适性、裂缝宽度等正常使用极限状态下的要求。

图3给出了两种结构在X，Y向（X向为纵向，Y向为横向，下同）地震作用下的层间位移角曲线。由图3可知，在地震作用下，异形柱框架的层间位移角都比矩形柱框架小，平均可以减小17.6%。这说明当框架柱的截面面积相同时，采用异形柱框架的抗侧刚度相对矩形柱框架大，当遭受到同等强度的地震作用时，由于层间位移角相对较小，门窗和填充墙这些非结构构件遭受破坏的程度会小很多，更能满足对抗震性能的要求。

2.2楼层最大位移

某一楼层的层间位移角与层高相乘则得到该楼层的层间位移。当把首层到某一楼层之间的层间位移叠加起来就得到该楼层的楼层最大位移。框架结构楼层位移计算是框架结构计算的重要内容之一。在实际进行结构计算时，一般并不直接对楼层最大位移这一指标进行限制，而是通过限制层间位移角这一指标来实现。

图4给出了异形柱框架和矩形柱框架在X，Y向地震作用下的楼层最大位移曲线。由图4可知，在地震作用下，两种结构随着层数的增加，楼层最大位移增速都趋于变缓，也即层间位移自底层往上都逐渐递减，属于框架结构典型的剪切型位移曲线。通过计算可知，异形柱框架的楼层最大位移平均可以减小18.1%，说明当框架柱的截面面积相同时，异形柱框架的抗侧刚度相对矩形柱框架大。

2.3楼层剪力

图5给出了两种结构在X，Y向地震作用下的楼层剪力曲线。由图5可知，在地震作用下，异形柱框架的楼层剪力都比矩形柱框架大。本工程的房屋高度为18 m，房屋高宽比值为2.1，而且整个结构的竖向布置均匀，没有收进，质量和刚度沿楼层的分布没有突变。由底部剪力法可知，由于异形柱框架的整体刚度比较大、周期相对较小，根据结构基本周期算出的水平地震影响系数较大。由底部剪力法的计算公式可知，其他参数都一样，则水平地震影响系数大的楼层剪力就大[11]。通过计算可知，异形柱框架的楼层剪力大约增加4.9%。

2.4剪重比

剪重比，也称剪力系数，为某一楼层对应于水平地震作用标准值的楼层剪力与该楼层重力荷载代表值的比值。剪重比是结构抗震性能的主要控制指标之一，主要目的是限制各楼层的最小水平地震剪力，确保周期较长的结构的安全[12]。表1给出了这两种结构布置方案的剪重比。

如果剪重比偏小且和规范规定的限值相差较大，则说明结构的刚度相对于水平地震剪力过小，这时宜适当加大柱、墙等竖向构件的截面尺寸，增加竖向构件的刚度[13]。根据规范，本结构的楼层最小剪重比为1.60%。由表1可知，这两种结构的每一楼层的剪重比都大于1.60%，都满足规范对楼层最小剪重比的要求。但如果剪重比過大，则说明结构的经济性较差，这时宜适当减少柱、墙等竖向构件的截面面积。由表1可知，在地震作用下，异形柱框架的剪重比略大，经济性稍差。

2.5结构自振特性

结构的自振特性是影响结构地震响应的重要因素。结构在水平地震作用下的变形、内力等都与结构的自振特性紧密相关[14]。因此为了更好地对结构的地震响应进行研究，需要准确得到与结构自振周期和振型有关的信息。表2给出了这两种结构在地震作用下的前3阶自振周期与振型。

由表2可知，异形柱框架的自振周期都比矩形柱框架小一些。由结构动力学可知，当质量不变时，结构的自振周期与刚度系数的1/2次方成反比。因为异形柱框架的抗侧刚度较大，所以自振周期相对较小。

结构的振型分为平动和扭转两种。当结构处于平动时，柱、墙等竖向构件的位移是一样的，所受的力也大致相等。当处于扭转时，结构周边构件的位移会比内部构件大，所受的力也大，造成周边构件在内部构件还没来得及充分发挥作用就先遭受破坏。一般来说平动要比扭转好[1518]。为了控制结构的扭转效应，减小扭转对结构产生的不利影响，一般来说，对于结构扭转为主的第1周期与平动为主的第1周期之比（也叫周期比），A级高度高层建筑不应大于0.9。周期比是控制结构扭转效应的有效指标之一，是对结构的扭转刚度与抗侧刚度之间的相对关系进行控制，目的是为了保证结构平面布置的规则性和合理性，以避免结构出现过大的扭转效应。由表2可知，这两种结构的前3阶振型都一样，周期比分别为0.851与0.837，都满足规范的要求，这说明上述两种结构平面布置方案都比较合理。由于异形柱框架的周期比相对较小，在控制结构的扭转效应方面更为有利。

3时程分析

3.1多遇地震下的弹性动力时程分析

3.1.1地震波的选取

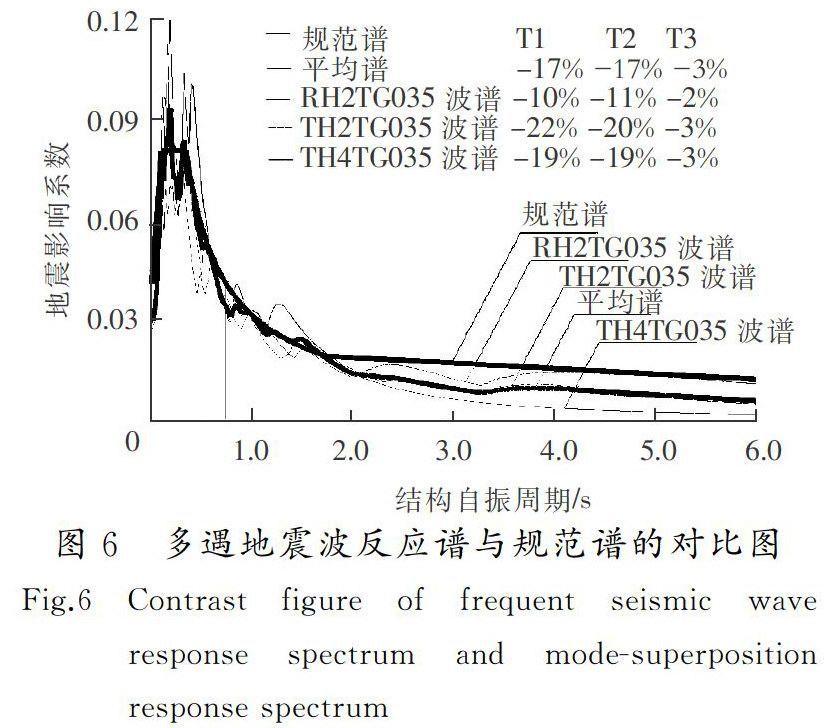
运用结构分析软件SATWE分别对矩形柱框架和异形柱框架进行多遇地震下的弹性动力时程分析。根据《建筑抗震设计规范》（GB 50011—2010）第5.1.2条对地震波的选取要求，经过多次试算[19]，最后选取了RH2TG035（人工波）、TH2TG035（天然波）以及TH4TG035（天然波）等3条地震波。图6为输入到矩形柱框架结构中的3条地震波反应谱与振型分解反应谱（规范谱）的对比图。

由图6可知，3条地震波的平均地震影响系数曲线（平均谱）与振型分解反应谱法所采用的地震影响系数曲线在统计意义上相符（结构主要振型的周期点上相差不超过20%），满足规范的要求。经检验，这3条地震波在输入到异形柱框架结构中时也同样满足规范的要求。

3.1.2多遇地震下的弹性时程分析

表3给出了两种结构的楼层最大位移和最大层间位移角的分析结果。由表3可知，在多遇地震下，和矩形柱框架相比，异形柱框架的楼层最大位移和层间位移角相对较小，抗震性能较为优越。

3.2罕遇地震下的弹塑性动力时程分析

3.2.1地震波的选取

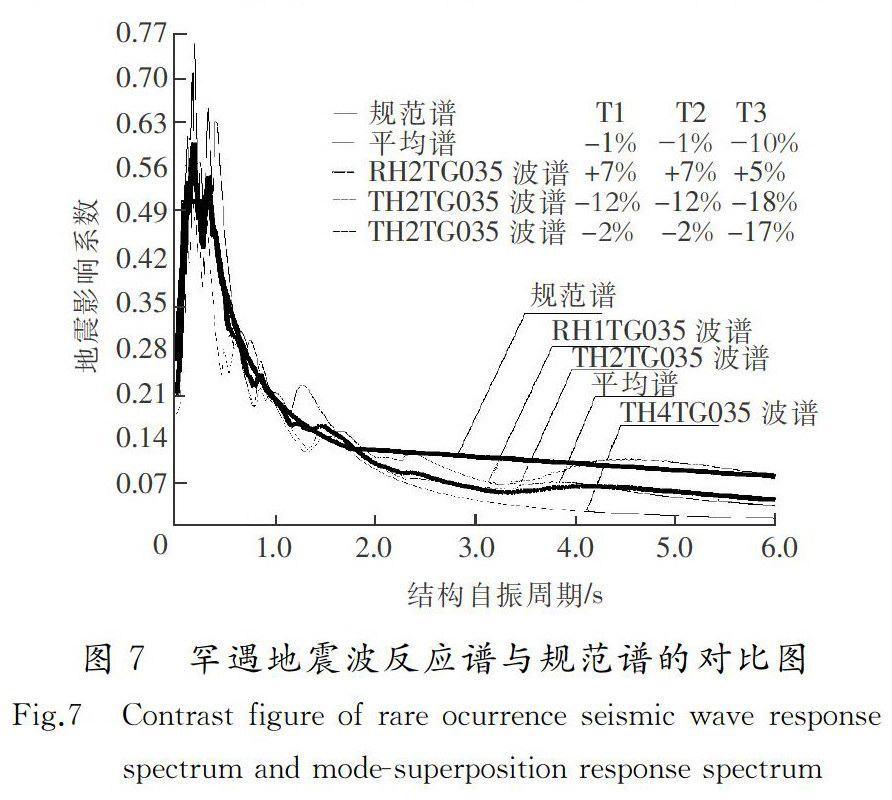
运用结构弹塑性动力时程分析软件EPDA读入SATWE模型，分别对矩形柱框架和异形柱框架进行罕遇地震下的弹塑性动力时程分析。根据规范对地震波的选取要求，经过多次试算，最后选取了RH1TG035（人工波）、TH2TG035（天然波）以及TH4TG035（天然波）等3条地震波。图7为输入到矩形柱框架结构中的3条地震波反应谱与振型分解反应谱（规范谱）的对比图。经检验，这3条地震波在输入到异形柱框架结构中时也同样满足规范要求。

3.2.2罕遇地震下的弹塑性时程分析

表4给出了两种结构的楼层最大位移和最大层间位移角的分析结果。由表4可知，在罕遇地震下，和矩形柱框架相比，异形柱框架的楼层最大位移和层间位移角相对来得小，抗震性能较为优越。

3.2.3塑性损伤情况分析

两种结构的塑性损伤发展情况如下（以RH1TG035波谱为例，记录时长为20 s，记录步长为0.02 s，地震波计算步数为1 000步）。

1）矩形柱框架第114步，底层梁首先开始出现塑性铰。第136步，底层梁塑性铰增多；2～4层也开始出现塑性铰，并逐渐增多。第179步，底层柱底端开始出现塑性铰，并逐渐增多；5层也开始出现少数几个梁塑性铰。第225步，除了边柱，其他底层柱都出现塑性铰；2～4层也有少数几个柱子出现塑性铰；2～4层的梁塑性铰继续增多。第342步，整个框架绝大部分的梁、柱塑性铰都出现完毕；从第342步到第1 000步就只有少数几个塑性铰出现。

2）异形柱框架第67步，底层梁出现第1个塑性铰。第87步，3～5层开始出现部分梁塑性铰。第107步，底层柱底端开始出现塑性铰；1～2层开始出现梁塑性铰，并逐渐增多。第119步，底层柱底端塑性铰逐渐增多；2～5层的梁塑性铰逐渐增多。第176步，大部分底层柱都出现塑性铰，2～4层的柱子也有若干根出现塑性铰；梁塑性铰也大部分出现。第210步，所有底层柱都出现塑性铰；绝大部分的梁、柱塑性铰都出现完毕。从第210步到第1 000步就只有少数几个塑性铰出现。

图8和图9分别给出了矩形柱框架和异形柱框架在弹塑性动力时程分析过程中所有曾经出现梁、柱塑性铰的位置分布图（以RH1TG035波谱为例）。

通过对比这两种结构的塑性损伤发展情况以及塑性铰分布图可知：1）从塑性铰的出现顺序上看，这两种结构都首先在梁中出现塑性铰，可以避免结构由于首先在柱中出现塑性铰而形成几何可变体系，满足规范对“强柱弱梁”的设计要求；2）从塑性铰的出现数量上看，和矩形柱框架相比，异形柱框架的梁塑性铰数量相对较多，当地震来临时，能更多地吸收地震能量；3）从塑性铰的出现时间上看，和矩形柱框架相比，异形柱框架的梁、柱塑性铰都出现得比较早，这主要是因为异形柱的延性比矩形柱差，当受到一定的水平荷载时，异形柱的柱肢会更早出现裂缝，进而导致异形柱框架的梁、柱塑性铰出现得比较早。

4经济性对比

在本工程的两种结构布置方案中，除了同一位置处的柱子分别采用矩形柱和异形柱外，其他构件都完全一样。在混凝土用量方面，由于柱子的截面面积相同，所以两种结构方案的混凝土用量一樣。在钢筋用量方面，运用PKPM相关模块软件进行配筋并统计工程量。

表5给出了两种结构方案的钢筋用量统计数据。图10给出了异形柱框架钢筋用量相对于矩形柱框架的百分比。由表5和图10可知，两种结构的板钢筋用量是一样的，这主要是因为板的布置以及所受的荷载都一样。异形柱框架的梁钢筋用量比矩形柱框架略微小一些，这主要是因为异形柱的柱肢比矩形柱的对应边长更长，导致异形柱框架的梁的计算长度略微减少，进而引起钢筋用量的减少。在柱钢筋用量方面，异形柱框架则大幅增加，相对矩形柱框架多使用了37.3%的钢筋，这主要是由异形柱的截面形状导致的。相比矩形柱，异形柱有两个柱肢，同一截面处箍筋的总长度更大，而且异形柱的截面角点数量也比矩形柱多，导致受力钢筋的用量也更大。从总的钢筋用量来说，异形柱框架大约比矩形柱框架多7.1%。

5结语

结合某6层框架住宅建筑，在保证同一位置处的框架柱截面面积相等的条件下，设计了异形柱框架和矩形柱框架两种结构方案，并进行了抗震性能和经济性的对比分析，得出了以下结论。

1）当框架柱截面面积相等时，异形柱框架的抗震性能总体上相对较好，具体表现为较大的抗侧刚度、较小的层间位移角、较小的楼层最大位移等。当遭受同等强度的地震作用时，异形柱框架的结构构件与非结构构件的变形相对较小，更容易达到抗震设计的“三水准”抗震设防目标中的“小震不坏，中震可修”的目标。

2）异形柱框架的周期比较小，更容易满足规范对周期比的要求，更有利于控制结构的扭转效应。当由于建筑功能上的需要，结构的平面布置不是十分规则合理，扭转效应比较明显时，如果建筑高度没有超过规范的要求，则可以考虑设计成异形柱框架。

3）在多遇地震和罕遇地震下，和矩形柱框架相比，异形柱框架的楼层最大位移和层间位移角都比较小，显示出更好的抗震性能。

4）在罕遇地震下，两种结构都能满足规范对“强柱弱梁”的设计要求，但异形柱框架的梁塑性铰出现数量更多，更有利于消耗地震能量。

5）和矩形柱框架相比，异形柱框架的柱钢筋用量大幅增加，经济性稍差一些。而且由于异形柱的截面形状的特点，钢筋的绑扎以及模板的搭设也相对费时费工。所以，在实际工程中，如果不是为了追求一个更加规整平滑美观的室内空间的话，矩形柱框架是一个更为经济的结构形式。具有较强的可应用性。

参考文献/References：

[1]刘红星.异形柱框架结构与普通框架结构抗震性能对比分析[D].重庆：重庆大学，2008.

LIU Hongxing， A Comparison of Seismic Behavior between Specially Shaped and Rectangular Column Frame Structures[D].Chongqing： Chongqing University， 2008.

[2]JGJ 149—2006，混凝土异形柱结构技术规程[S].

[3]胡杰云，裴丽敏，杨予.多层异形柱住宅结构优化设计与实例分析[J].山西建筑，2012，38（26）：4850.

HU Jieyun， PEI Limin， YANG Yu. Optimal design and case analysis of residential structure with specialshaped column[J].Shanxi Architecture，2012，38（26）：4850.

[4]WANG Mingdong， NI Zhengyin. optimization and suggestions of design for RC frames with specialshaped columns based on Chinese specification[C]//Proceedings of 3rd International Conference on Civil Engineering， Architecture and Building Materials （CEABM 2013）. [S.l.]：[s.n.]， 2013：36.

[5]王依群，曹茹.使用PKPM软件计算异形柱结构的注意事项[J].结构工程师，2010，26（4）：714.

WANG Yiqun， CAO Ru. Key issues in design of structures with specially shaped columns by using PKPM software[J].Structural Engineers，2010，26（4）：714.

[6]张冀男.住宅设计的几点思考[J].河北工业科技，2011，28（4）：283284.

ZHANG Jinan. Some viewpoints about house design[J].Hebei Journal of Industrial Science and Technology，2011，28（4）：283284.

[7]李清.结构分析软件SATWE结构设计时要注意的问题[J].四川建筑科学研究，2009，35（2）：5456.

LI Qing. Some problems need to be noticed in the structure design with the analytical software SATWE of structure[J].Sichuan Building Science，2009，35（2）：5456.

[8]SHI Yanghang， ZHANG Dayong， WANG Danfang. Study on seismic performance and conceptual design of 3dframes with specialshaped columns[C]//Proceedings of International Conference on Earthquake Engineering1st Anniversary of Wenchuan Earthquake. [S.l.]：[s.n.]，2009：389394.

[9]蔣欢军，吕西林.钢筋混凝土框架结构层间位移角与构件变形关系研究[J].地震工程与工程振动，2009，29（2）：6672.

JIANG Huanjun， LYU Xilin. Study on the relationship between story drift and element deformation for reinforced concrete frames[J].Earthquake Engineering and Engineering Vibration， 2009， 29（2）： 6672.

[10]林盼盼.某异形柱框架结构抗震性能分析[J].世界地震工程， 2014， 30（4）： 229233.

LIN Panpan. Seismic performance analysis of RC frame structure with specialshaped columns[J].World Earthquake Engineering， 2014， 30（4）： 229233.

[11]JI Dongyu. Force calculation for specialshaped column frame structure of under earthquake action [C]//Proceedings of International Conference on Advanced Engineering Materials and Architecture Science （ICAEMAS 2014）. [S.l.]：[s.n.]，2014：561564.

[12]李当生.谈剪重比的概念和合理控制[J].工程建設与设计， 2009， 57（9）： 2527.

LI Dangsheng. The concept and reasonable control of shearweight ratio[J].Construction & Design for Project，2009，57（9）：2527.

[13]杨星. PKPM结构软件从入门到精通[M].北京：中国建筑工业出版社，2008.

[14]柯江，高兑现.异形柱框架结构与矩形柱框架结构受力特性比较[J].建筑结构，2006，36（2）：4446.

KE Jiang， GAO Duixian. Contrastive analysis of mechanics characteristic between specialshaped and rectangular column frame structures[J]. Building Structures，2006，36（2）：4446.

[15]XU Dongqiang， HE Meimei. Seismic performance analysis of the specialshaped frame column structure on multidimensional seismic [C]//Proceedings of International Conference on Civil Engineering and Transportation （ICCET 2011）.[S.l.]：[s.n.]，2011：16441648.

[16]李英民，韩军，刘建伟.建筑结构抗震设计扭转周期比控制指标研究[J].建筑结构学报，2009，30（6）：7785.

LI Yingmin， HAN Jun， LIU Jianwei. Study on torsional period ratio control index for seismic design of building structures[J].Journal of Building Structures，2009，30（6）：7785.

[17]张学辉，董洁.八度区不等层高异形柱框架抗震性能研究[J].河北工业科技，2012，29（1）：3539.

ZHANG Xuehui， DONG Jie. Seismic behavior of unequal height storey frame with specially shaped columns in eight intensity zone[J].Hebei Journal of Industrial Science and Technology， 2012， 29（1）： 3539.

[18]张俊文.结构整体计算控制指标的应用[J].山西建筑， 2014， 40（34）： 4647.

ZHANG Junwen. On application of controlled indexes of structural overall calculation[J].Shanxi Architecture，2014，40（34）：4647.

[19]陈康华，郭远翔.弹性动力时程分析中地震波的选取方法研究[J].河北工业科技，2012，29（1）：4043.

CHEN Kanghua， GUO Yuanxiang. Selection of earthquake waves in elastic timehistory dynamic analysis[J].Hebei Journal of Industrial Science and Technology， 2012，29（1）：4043.