基于改进谱聚类算法在图像分割中的应用

王贝贝 杨明 燕慧超

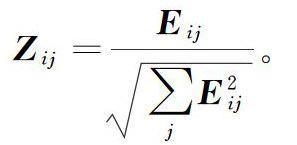
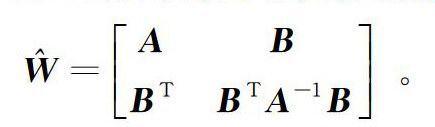
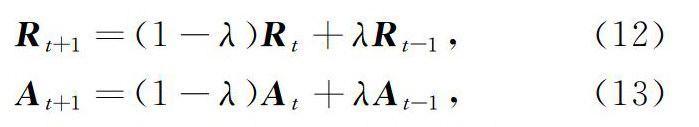
摘要：为解决谱聚类算法应用于图像分割时，相似矩阵内存占用较大甚至满溢以及后续计算量大的问题，利用Nystrom方法随机获取一部分样本点，根据样本点和样本点、样本点和非样本点2种相似关系近似表征所有像素点的相似性，得到原图像的近似相似矩阵。在构建上述所需2种相似关系的相似矩阵时，距离度量采用余弦函数。结果表明，采用近邻传播聚类算法代替kmeans算法對得到的低维向量子空间聚类，克服了聚类过程对初始值的敏感性，得到的分割结果较稳定，4幅真实图片也验证了研究算法的优越性。改进的谱聚类算法为图像分割的稳定性研究提供了依据。

关键词：图像处理；图像分割；谱聚类；Nystrom方法；余弦距离；AP算法

中图分类号：TP391文献标志码：Adoi： 10.7535/hbgykj.2018yx01010

Application of improved spectral clustering algorithm in image segmentation

WANG Beibei， YANG Ming， YAN Huichao

（School of Science， North University of China， Taiyuan， Shanxi 030051， China）

Abstract：To solve the problem of large usage of the similar matrix memory， even overflowing，and the large amount of calculation when spectral clustering algorithm is applied in image segmentation， a part of sample points are obtained by using the Nystrom method， according to the two similarity relations between sample points and sample points， sample points and nonsample points to get the similarity relation of all pixel points， then the approximate similarity matrix of the original image is got. In building the two block similar matrixs required in Nystrom， cosine function is used to overcome the absoluteness of Euclidean distance in the distance measurement . In this paper， the nearest neighbor propagation clustering algorithm is used to replace the kmeans algorithm to overcome the sensitivity to the initial value in the clustering process， thus obtaining a more stable effect. The experimental results of the 4 real images show that the method is far superior， and the improved spectral clustering algorithm provides reference for the stable study of image segmentation.

Keywords：image processing； image segmentation； spectral clustering； Nystrom method； cosine distance； AP algorithm

图像分割是模式识别中的一个重要研究领域，它的目标是根据对图像的像素属性（如灰度、颜色和纹理等）进行划分从而实现对图像的分割。在实际应用中，对同一幅图像，不同的研究人员可能需要提取不同的信息，人们需要也即感兴趣的区域称为前景，其余区域称为背景。图像分割就是把图像分成各具特性的区域并提取出感兴趣目标的技术和过程[12]。

聚类算法在图像分割中应用得较为广泛，其中谱聚类算法是依托谱图划分理论演化而来的，优于kmeans算法[3]、FCM算法[4]等传统算法，这是因为其不受样本空间形状的限制，能收敛于全局最优解的特性。在进行图像分割时[5]，谱聚类算法将图像的每个像素点视为对应无向图的一个节点，用像素矩阵来表达图像，这样就把图像的分割问题转换为对数据的聚类问题，此时，再根据某种距离准则构造新数据集的相似矩阵，新矩阵中的元素表示任意两像素点间的相似度，若需要分割的图像像素点个数为m×n，则它对应的相似矩阵的维数为（m×n） ×（m×n），计算量大，占用内存也较大。为解决该问题，文献＼[6＼]基于Nystrom方法提出了一种近似方法估计相似矩阵，首先解决一个小的随机像素子集的分组问题，然后将该解外推到图像或图像序列中的全部像素组中，这样能简单、高效地估计出相似矩阵的主特征向量，分割的结果也较稳定。JIAO等[7]将谱聚类算法与网格结合，通过将原始网格模型嵌入到光谱空间中，来解决分割问题。首先根据最小规则确定网格凹区，然后通过考虑网格显著性和曲率信息定义拉普拉斯矩阵，最后用特征分解法计算拉普拉斯矩阵的前k个特征向量，将原始网格嵌入到一个k维的光谱空间中，利用混合高斯方法实现最终的分割。李杨等[8]研究了在不同的颜色空间中，不同的距离测度构造的相似矩阵对分割结果的影响，通过分析比较6种不同相似度构造方法的分割效果，得出无论在RGB还是HSV颜色空间下，采用余弦距离公式得到的分割效果都是最优的。李小斌等[9]设计了一个递归的多尺度分层分割算法，解决了谱聚类应用于图像分割时权值矩阵的特征值和特征向量难以计算的问题，首先定义像素点与类之间的距离，在研究对图像的像素进行抽样的基础上得到一个抽样数定理，对少量的采样点采用SCAWM聚类，然后再按距离最近原则对大量的非采样点聚类，引入尺度因子使图像从“粗”到“细”完成分割。

1经典谱聚类算法研究

在数据聚类和图像分割中，结合谱图理论的谱聚类算法一直表现很好，并已成功用于解决数据聚类和图像分割问题，而对图像的分割实质也是对数据的聚类，因为对图像的分割是对代表图像信息的像素点集X=（x1，x2，…，xn）的聚类。谱聚类算法在数据聚类中的高性能和较易实现，近年来吸引了越来越多人的关注。其本质是将聚类问题转化為图的最优划分问题，将图像映射为带权无向图，图的每个节点对应一个像素，每对像素之间的相似性作为无向图的边，通过边上的权值构造相似性矩阵。大致过程可归纳为3步。

1）根据某种相似性度量构建待聚类数据集的相似矩阵W=[wij]；

2）计算规范化拉普拉斯矩阵L=D-12WD-12的前k个特征值及其对应的特征向量，其中D=diag（d1，d2，…，di，…，dn），di=∑nj=1wij，构建特征空间的向量矩阵V=[v1，v2，…，vk]∈Rn×k；

3）对上述得到的向量矩阵用经典聚类算法进行聚类。

然而，在传统的谱聚类算法中依然存在如下问题：

1）常用的基于相似性度量的高斯核函数：

W（xi，xj）=exp（-‖xi-xj‖2/2σ2）（1）

不能充分反映数据集的复杂空间分布，当集群是复杂的流形结构时不适用[10]；

2）当数据集的规模N比较大时，总的时间复杂度和空间复杂度分别达到了O（N3）和O（N2），储存和分解一个大的相似矩阵就比较困难，尤其是对一个图像。

2改进谱聚类算法

2.1基于Nystrom方法的谱聚类

谱聚类算法的瓶颈之一是相似矩阵的构建及其计算，首先解决计算量大的问题。

因为相似矩阵中元素的个数是样本数的平方，例如：一幅由512×512个像素组成的图像，需要计算262 144×262 144维的相似矩阵，计算量较大，计算时间长，很可能会引起内存满溢的情况。有研究表明，基于Nystrom方法的谱聚类能在很大程度上提升谱聚类算法的性能。

Nystrom方法是一种基于积分方程，计算矩阵特征值和特征向量的近似方法，适用于对称正定矩阵。其基本思想是采用随机采样的方式获得一定的样本点，用样本点与非样本点之间的相似性来近似估计非样本点之间的相似性[11]。若原图像的像素总数为N，从中随机采集m个样本像素点（mN），则非样本点的个数为n=N-m，相似性矩阵W可以表示为

式（2）中A∈Rm×m，B∈Rn×m，C∈Rn×n。矩阵A表示随机采集的m个样本像素点之间的相似矩阵，矩阵B表示随机采集的m个样本像素点与n个非样本像素点之间的相似矩阵，矩阵C表示n个非样本像素点之间的相似矩阵。因为mN，所以矩阵C计算量如同未采样前的矩阵的计算量一样巨大，故通过Nystrom采样方法用A和B估计C[12]。

先将矩阵A对角化为A=UΛUT，其中Λ是一个对角矩阵，非零元素对应矩阵A的特征值，再将特征向量U扩展为相似矩阵W的近似特征向量：

由式（3）可知Nystrom采样方法是用BTA-1B估计C，即C=BTA-1B。由此，便可以用较少的样本像素点逼近全部点的相似矩阵W。

笔者得到了相似矩阵和其主特征向量的近似估计和。但是应用到谱聚类中，需要的是特征系统D-1/2WD-1/2的主特征向量。所以接下来，计算的行和，将其对应为对角矩阵D中对角线上的元素，估计矩阵的行和为

若矩阵A正定，接下来便解决估计特征向量的正交化问题。令A1/2表示A的对称正定平方根，并定义Q=A+A-1/2BBTA-1/2，将Q对角化为Q=UQΛQUTQ，则W可正交化为=VΛVT，其中：

经过上述变换，则可取矩阵V的前k个向量构成矩阵E，再对矩阵E的行向量聚类，由此便可减少在谱聚类算法中的计算量。

2.2基于余弦函数的相似矩阵

在上述过程中，笔者已经用Nystrom方法解决了相似矩阵计算量大的问题，该节解决的则是相似矩阵的构建问题，也即采取合适的高斯度量来表示相似矩阵。图像的相似度矩阵由该图像中各像素之间的相似度构成，而高斯核函数中的欧氏距离度量只考虑绝对距离，在考虑相对距离时，余弦距离比其他距离表现出更好的实际意义。

假设待分割的图像包含N个像素点，每个像素有p个特征数，则该图像可表示为A∈RN×p，这里A=[a1，a2，…，aN]T，其中ai∈Rp，1≤i≤N，用余弦函数得到的图的相似度矩阵可表示为W=[wij]N×N，其中：

如果对数据集A进行归一化，即有‖ai‖=‖aj‖=1，则像素点xi到像素点xj的余弦相似度可简化为wij=aiaj，相应地相似矩阵W简化为W=[wij]N×N=AAT。由此，图像的相似度矩阵可由图像矩阵A和其转置相乘得到。

2.3近邻传播聚类算法

在2.1节最后所得的矩阵E的每一行都对应一个像素点，这节需要做的则是将新得到的矩阵相应的数据点进行聚类处理，传统谱聚类算法的最后一步在采用kmeans聚类算法时，对初始值较敏感，需要人为初始化类的个数，分割结果不稳定，即取不同的初始值得到的分割效果也不同。为解决该问题，本研究引入近邻传播算法（AP算法）[13]，该算法是2007年刊登在《科学》期刊上的的一篇文章提出的一种新型的聚类算法，事先不需要知道类的数目，通过对矩阵进行迭代收敛，最终更新到稳定的类中心，然后计算每一个数据点与所有类中心的相似度的大小，将其划分到相似度最大的类中心，每个类中心及其划分到该类中心的其他数据点即组成一个类别。

近邻传播算法需要首先构建新的数据集中点与点之间的相似度矩阵，相似度用欧氏距离度量即可。Sij=-‖yi-yj‖2，i≠j，然后把相似度矩阵S（i，j）=-‖yi-yj‖作为输入，交换数据点间的信息，交换方式主要依靠2种度量：吸引度和归属度。吸引度r（i，k）是数据点yi发送到候选类中心yk的信息，表示点yi对候选类中心点yk的支持程度，该值越大，则表明点yk作为点yi的类中心的可能性越大；归属度a（i，k）是候选类中心yk发送给数据点yi的信息，表示候选类中心yk作为点yi的类中心的合适程度，该值越大，则表明点yi选择点yk作为其类中心的可能性越大。在算法迭代过程中，每个数据点都会进行2种信息的交替更新，更新公式为

当每个数据点都进行了上述2次的信息更新后，算法也迭代了1次。在运算过程中，引入阻尼系数λ∈[0，1），来避免AP算法的大幅度震荡，迭代次数和每次迭代的结果都会随着阻尼系数的改变而改变：λ取值较小时，迭代的次数会较少，但是运算过程中的数值波动性却较大，此时得到的较大图像的收敛结果不理想；λ取值较大时，迭代的次数虽会较多，但图像的收敛效果较理想。本文取λ=0.9，对应的吸引度矩阵和归属度矩阵更新公式如下：

其中t表示迭代次数。数据点yi的聚类中心即是令r（i，k）+a（i，k）取最大值的点yk。

2.4改进谱聚类算法

谱聚类算法在进行图像分割，初始化相似矩阵时会出现内存满溢的情况，无法进行后续工作。为了解决该问题，本研究提出一种改进的谱聚类算法——INJW算法，对预处理的图像，研究利用Nystrom方法随机获取一定的样本点。先构建样本点与样本点间的相似矩阵、样本点与非样本点间的相似矩阵，再根据式（4），用这2个分块矩阵来近似表征所有像素点间的相似矩阵。在构造上述所需的分块矩阵时，距离度量采用余弦函数，克服欧氏距离的绝对性，由此便完整的得到了谱聚类算法第1步所需的相似矩阵；第2步所需规范化拉普拉斯矩阵的主特征向量为式（8）的前k个向量；最后对这个低维向量子空间聚类时采用近邻传播聚类算法代替kmeans算法，克服了聚类过程对初始值的敏感性。

1）预处理输入图像G，随机抽取1%的样本像素点，根据式（9）的余弦函数构造像素点的分块相似性矩阵A和B，得到待处理图像的相似矩阵为

2）计算拉普拉斯矩阵L=D-1/2D-1/2的前k个特征向量，即根据式（8）计算出矩阵V，并取V的前k个最大特征值对应的特征向量，得到新的特征矩阵为E。

3）将矩阵E的行向量规范化为单位矩阵Zij，

4）矩阵Zij的每一行对应原图像的一个像素点，用AP算法对其进行聚类。

5）根据步骤4）得到的聚类结果确定所有像素点的类别：当矩阵Zij的第i行对应第j类时，像素点Ei对应第j类。

3结果与分析

为了验证本研究算法的性能，在操作平台为64位Windows 7系统、CPU为Intel（R） Core（TM）i52450M（2.50 GHz）、4 GB内存的计算机和Matlab R2014a中进行实验。实验图片来自美国南加州大学的USISIPI图像数据库和美国加州大学伯克利分校的BSDB標准测试图像数据库中的4幅图像，对比算法为k均值聚类算法（kmeans）、基于规范化拉普拉斯矩阵的谱聚类算法（NJW），实验对比图见图1—图4。

图1是数据库中4幅图的原始图像：图1 a）和图1 b）分别是人物图lena和cameraman，图1 c）是动物图ducks，图1 d）是实物图airplane。图2是kmeans算法的分割结果，由于该算法对初始值较敏感，且取不同的分割数时结果也不相同，故在编程时设置k分别取2，3，4，5，6，且在程序运行20次后选择最优直观分割图，其中lena图的最优分割为k=3，cameraman图的最优分割为k=4，ducks图的最优分割为k=6，airplane图的最优分割为k=4。 图3是基于规范化拉普拉斯矩阵的谱聚类算法（NJW）的分割结果图。图4是本文算法INJW——改进的谱聚类算法的分割结果图。

从总体上来看，kmeans算法分割出来的图较模糊，前景和背景区域都含有很多噪声点，NJW算法的分割结果图较纯净，本文算法的分割效果图最清晰，不管是人物还是动物，前景和背景区分都较明显，区域对比度、区域内部均匀性都较前2种算法明显提高。

1）人物lena图kmeans算法的分割图中人物的帽子、头发和五官都已模糊化，且前景、背景混为一体；NJW算法的分割图虽然前背景明显，但人物的五官不是很清楚，鼻梁和脸颊并没有分割开；本研究算法运行出来的分割图中帽子和头发都更加细腻，五官清晰。

2）人物cameraman图kmeans算法的分割图中右侧有少量噪声点，前景人物和背景海水混为一体；NJW算法的分割图则把前景人物分割出来，但是人脸五官不明显，背景的轮廓没有分割出来；本研究算法较好地分割开前景和背景，海上的建筑物高楼虽然并没有完全分割出来，但总体上还是达到较理想的效果。

3）动物ducks图3种算法都分割出前背景，树干上的涂白剂都和未喷涂部分分割开来，鸭子和海水也分割开。但是很明显，kmeans算法分割出来的鸭子轮廓不明显，且远处的3只已经模糊化；NJW算法则把靠岸的3只鸭子和岸边混为一体；本研究算法细节分割的更加明显，鸭子的嘴巴也能显露出来。

4）实物airplane图该幅图不仅要把前景的飞机和背景的天空、雪山分割开，还要准确地分割出飞机上的图案和字母。kmeans和NJW算法都没能达到理想的效果，本研究算法能分割出机尾的字母和数字F16，以及飞机上的五角星标志。

4结论

每一幅图像都能用对应的像素矩阵表示，所以对图像的分割本质上是对代表其像素点的数据的分割。谱聚类算法用于分割图像时，最大的困难是相似矩阵的构造，经常会出现内存不足甚至满溢的情况，即使能计算出，时间成本也较高。本研究结合Nystrom采样方法，很大程度上减少了计算的复杂度，且对相似矩阵中距离度量做了改进，用余弦距离代替传统欧氏距离。最后阶段，以近邻传播算法取代kmeans算法对k个特征主向量进行聚类。实验结果验证了本文算法的稳定性和有效性，分割出来的图像质量有了很大提升，接下来的工作重点将放在对前背景较复杂图像的分割。

参考文献/References：

[1]周莉莉， 姜枫. 图像分割方法综述研究[J]. 计算机应用研究， 2017， 34（7）：19211928.

ZHOU Lili， JIANG Feng. Survey on image segmentation methods [J]. Application Research of Computers， 2017， 34（7）：19211928.

[2]章国红，辛斌杰.图像处理技术在纱线毛羽检测方面的应用[J].河北科技大学学报，2016，37（1）：7682.

ZHANG Guohong， XIN Binjie. Application of image processing technology in yarn hairiness detection[J]. Journal of Hebei University of Science and Technology， 2016，37（1）：7682.

[3]SHI B， PANG Z F， XU J. Image segmentation based on the hybrid total variation model and the kmeans clustering strategy[J]. Inverse Problems & Imaging， 2016， 10（3）：807828.

[4]DUBEY Y K， MUSHRIF M M. FCM clustering algorithms for segmentation of brain MR images[J]. Advances in Fuzzy Systems， 2016（3）：114.

[5]BAILLARD C， HELLIER P， BARILLOT C. Segmentation of brain 3D MR images using level sets and dense registration[J]. Medical Image Analysis， 2001， 5（3）：185194.

[6]FOWLKES C， BELONGIE S， CHUNG F， et al. Spectral grouping using the Nystrm method [J]. Pattern Analysis and Machine Intelligence IEEE Transactions， 2004， 26（2）：214225.

[7]JIAO X， WU T， QIN X. Mesh segmentation by combining mesh saliency with spectral clustering[J]. Journal of Computational & Applied Mathematics， 2018，329：134146.

[8]李揚， 陆璐， 崔红霞. 谱聚类图像分割中相似度矩阵构造研究[J]. 计算机技术与发展， 2016， 26（7）：5558.

LI Yang， LU Lu， CUI Hongxia. Research on similarity matrix structure in spectral clustering image segmentation [J]. Computer Technology and Development， 2016， 26（7）：5558.

[9]李小斌， 田铮. 基于谱聚类的图像多尺度随机树分割[J]. 中国科学， 2007， 37（8）：10731085.

[10]YANG Y， WANG Y， XUE X. A novel spectral clustering method with superpixels for image segmentation[J]. Optik International Journal for Light and Electron Optics， 2016， 127（1）：161167.

[11]管涛， 李玉玲. 大规模矩阵降维的随机逼近方法[J]. 数学的实践与认识， 2016，46（24）：184193.

GUAN Tao， LI Yuling. Stochastic approximation method for largescale matrix reduction[J]. Mathematics in Practice and Theory， 2016，46（24）：184193.

[12]BERGH F V D， ENGELBRECHT A P. Training product unit networks using cooperative particle swarm optimisers[J]. International Joint Conference on Neural Networks， 2001，1：126131.

[13]FREY B J， DUECK D. Clustering by passing messages between data points[J]. Science， 2007，315（5814）：972976.