缝洞型碳酸盐岩油藏试井分析模型研究

邢翠巧 尹洪军 李兴科 赵梓瑜 付京

摘要：针对缝洞型碳酸盐岩油藏经过构造及岩溶作用之后大尺度溶洞、裂缝发育比较成熟、尺度差别不大的情况，建立了溶洞及裂缝发育的双孔模型。利用裂缝及溶洞中流体的流动方程，建立了考虑井筒储集系数及表皮系数影响的封闭边界油藏双孔单渗试井分析模型；利用Laplace变换法和Stehfest数值反演法算法对数学模型进行求解，得到实空间下无因次井底压力的解析解；绘制并分析了试井典型曲线，并对试井典型曲线特征及不同参数对试井压力响应曲线的敏感性进行了分析。结果显示，所建立的试井分析模型能够反映缝洞型碳酸盐岩油藏实际储层特征和流体的流动机理。研究结果为进一步完善和发展缝洞型碳酸盐岩油藏试井模型、丰富试井解释方法提供了理论参考。

关键词：渗流力学；缝洞；碳酸盐岩；试井分析；双孔单渗

中图分类号：TE344文献标志码：Adoi： 10.7535/hbgykj.2018yx01006

Research of the fractured vuggy type carbonate reservoirs well test analysis model

XING Cuiqiao1， YIN Hongjun1， LI Xingke1，2， ZHAO Ziyu1， FU Jing3

（1. College of Petroleum Engineering， Northeast Petroleum University， Daqing， Heilongjiang 163318， China；2. Oil and Gas Engineering Institute of the Jilin Oilfield， Songyuan， Jilin 138000， China；3. Mewbourne School of Petroleum & Geological Engineering， The University of Oklahoma， Norman OK， Oklahoma 73019， USA）

Abstract：The fractured vuggy type carbonate reservoirs follow the structure and karst function processes， large scale caves and fractures are mature， and there's little difference in scale. Therefore， the formation of caves and fractures can be regarded as a double porosity model. Considering the flow of fluid in fracture and cave， a double porosity of single permeability well test model with sealed boundary reservoir is established considering the influence of wellbore storage and skin factor. The mathematical model is solved by Laplace transform and Stehfest numerical inversion algorithm， and the solution of dimensionless well bottom pressure in real space is obtained. The typical curves of well test are plotted and analyzed. The characteristics of well test typical curves and the influence of sensitivity with different formation parameters to well test pressure response curves are analyzed. The results of well test analysis model established in this paper can reflect the characteristics of reservoir and flow mechanism of fluid in fractured vuggy carbonate reservoir. It lays a theoretical foundation for further improving and developing well test model of fractured vuggy carbonate reservoir and enriching well test interpretation method.

Keywords：mechanics of flow through porous media； fractured vuggy； carbonate reservoir； well test analysis； double porosity and single permeability

縫洞型碳酸盐岩油藏在经过不同时期的构造作用和不断的岩溶作用之后，储层中空间形态多样，储层类型复杂[15]。缝洞型碳酸盐岩油藏中流体的有效储存介质为大尺度溶洞及裂缝，其中裂缝是主要的流动通洞，其中的大尺度溶洞、裂缝及溶蚀孔洞高度分散，这就导致其中流体流动的多样性。缝洞型碳酸盐岩油藏复杂的储层特征和流动机理决定了其试井模型与常规的砂岩油藏、裂缝型碳酸盐岩油藏有着本质的区别[613]。

目前的缝洞型碳酸盐岩油藏的试井分析理论还不成熟，而且多存在着试井解释结果与实际储层特征不符的问题。随着缝洞型碳酸盐岩油藏储层的开发，研究含有大尺度溶洞、裂缝的试井分析模型对于这类油藏的试井解释和油田开发动态预测具有重要意义。1985年，NELSON[14]利用测井资料对裂缝进行了定性分析，并分析了自然电位、自然伽马、井径、双侧向电阻率、声波、密度和中子等参数对裂缝的响应特征，发现碳酸盐岩的测井响应具有“一小、二高、三低”的特点。2008年，陈俊昌等[15]对塔中地区油藏储层特征进行了分析，采用统计方法，对多口井的实际试井曲线进行分类，通过这种方法，对几种缝洞型储层的试井曲线典型特征有了进一步的认识。2001年，谭承军等[16]对塔河油田不同储层类型油井产能进行了统计，给出了洞穴型、孔洞型和裂缝型3种储层类型的产能特征以及稳产能力，为定性认识和研究缝洞型碳酸盐岩油藏的产能提供了实际的参考价值，具有重要的实用意义。2005年，康志江等[17]分析了塔河缝洞型油藏储层及生产动态特征和流体的流动机理，对塔河缝洞型油藏进行分类研究，主要是对其含水率变化进行了分析。2007年，马立平等[18]从油藏物质平衡基本原理出发，建立了缝洞型油藏物质平衡方程。2008年，彭小龙等[19]将缝洞体看作零维模型，建立了一個缝洞体和2个缝洞体的试井模型，其中在裂缝与洞之间会发生拟稳态窜流，绘制了压力响应曲线。2012年，刘洪等[20]将溶洞视为等势体，利用溶洞质量守恒原理建立了井钻遇大尺度溶洞的缝洞型碳酸盐岩油藏渗流数学模型，利用边界元方法得到了压力响应曲线。

以往对于缝洞型碳酸盐岩油藏试井模型的建立大多是基于等效连续介质理论，认为裂缝、溶洞及溶蚀孔洞均匀地分布在整个研究区域，所有介质中流体的流动都是符合达西渗流规律。但是这些方法只是适用于表征单元体存在且尺度较小的时候，对于存在大尺度溶洞及裂缝的缝洞型碳酸盐岩油藏来说，等效连续介质理论是不适用的，以往所建立的等效连续介质模型是不能应用到缝洞型油藏的试井解释中的[2122]。随着对缝洞型碳酸盐岩油藏不断认识和深入研究，考虑到缝洞型碳酸盐岩油藏中基质不具有渗流能力，因此，本文建立了能更好描述缝洞型油藏储层特征和流体流动机理的双孔单渗模型，将缝洞型碳酸盐岩油藏看成是2个系统，分别是溶洞系统和裂缝系统，这样就充分考虑了缝洞型油藏的地质情况，考虑了介质的非连续性与多尺度性。在流体渗流的过程中，认为溶洞中流体向裂缝系统中的窜流，流体通过井底周围的大尺度裂缝流到井筒采出。因此，建立了考虑井筒储集系数和表皮系数的圆形封闭油藏双孔单渗试井分析模型，并通过Laplace变换法和Stehfest数值反演法算法对数学模型进行了求解，绘制并分析了试井典型曲线特征，对不同参数对试井典型曲线的影响（敏感性分析）进行了分析。

1物理模型

对于缝洞型碳酸盐岩油藏，建立的双孔单渗试井物理模型如图1所示。

双孔单渗试井物理模型的基本假设条件：

1）地层流体单相且微可压缩；地层岩石微可压缩，且压缩系数为常数。

2）在油藏未被开采之前，储层中任一位置处的压力为原始地层压力pi。

3）地层为圆形，各向同性，水平等厚，地层中溶洞及裂缝高度发育。

4）忽略重力和毛管力的影响，考虑表皮效应和井筒储集系数的影响。

5）油井以定产量q生产。

6）溶洞及裂缝中流体的渗流为达西渗流，渗流过程中为等温，无任何特殊的物理和化学现象发生；溶洞中的流体通过窜流流到裂缝，裂缝为流体流动的主要通道，流体通过裂缝（主要的渗流通道）流到井底，然后再通过油井将流体采出。

2数学模型

2.1模型的建立

将运动方程、岩石及流体的状态方程代入到连续性方程中，得到流体流动的偏微分方程。

裂缝的基本微分方程：

式中：pi为原始地层压力，MPa；pj为地层压力，MPa；pw为井底压力，MPa；K为渗透率，μm2；为孔隙度，无量纲小数；rw为油井半径，m；B为体积系数；h为油层厚度，m；re为油藏半径，m；q为油井产量，m3/d；μ为流体黏度，mPa·s；S为表皮系数；下标f和v分别为裂缝、溶洞；α为形状因子。

2.2模型的解

定义无因次量：

式中：pjD为无因次地层压力；reD为无因次油藏半径；tD为无因次时间；ω为裂缝储容比；λ为窜流系数；rD为无因次半径；CD为无因次井筒储集系数。

利用定义的无因次量，对式（1）—式（6）进行无因次化，得到：

利用Stehfest数值反演法算法将Laplace空间下的解转换为实空间的解，最终得到实空间下井底压力的解pwD。

3试井曲线分析

3.1试井典型曲线特征分析

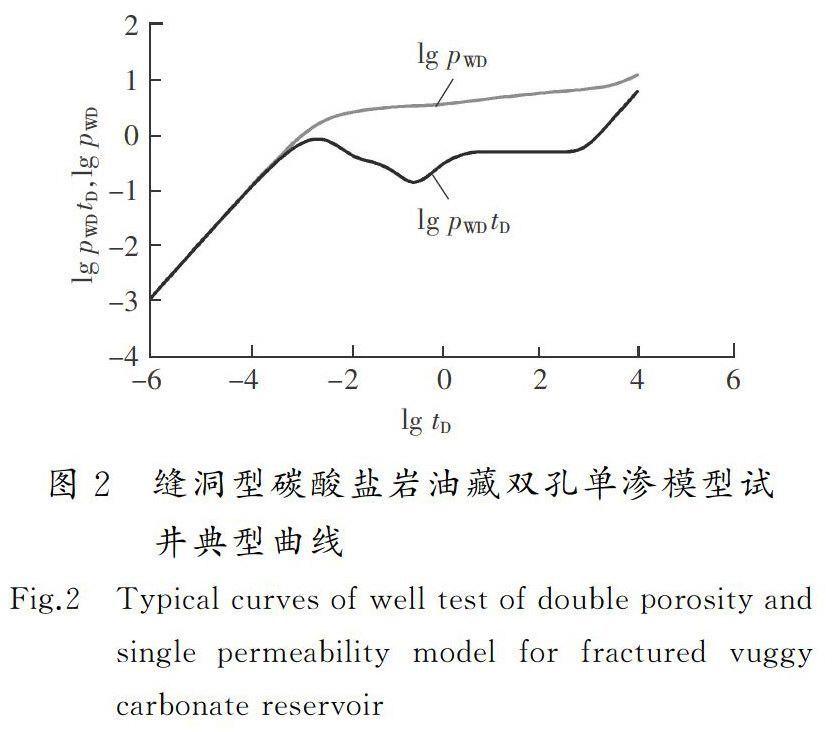
通过编程计算，对模型进行求解，并利用计算得到的实空间下不同时间对应的井底压力及压力导数数据绘制试井双对数曲线，并对考虑井筒储集和表皮系数的缝洞型碳酸盐岩油藏试井典型曲线特征进行分析，同时进行参数的敏感性分析。考虑井筒储集和表皮系数的缝洞型碳酸盐岩油藏双孔单渗模型试井典型曲线如图2所示。

通过分析图2的试井典型曲线可知，第1阶段为早期井筒储集阶段：这段中的压力及压力导数曲线在早期会重合，主要受井筒储集系数和表皮系数的影响，当井筒储集越大时，压力及压力导数曲线早期阶段就会越长，表明井筒储集效应越严重，同时也会造成井储时间越长。表皮系数越大，即井底周围的污染越严重，流体从油层流动到井底所消耗的压力越大，所以压力曲线的位置越高；且随着表皮系数的增大，压力导数曲线峰值也越高，驼峰就会越陡峭，下倾越陡，同时峰值出现的时间也会越迟。第2阶段为窜流阶段：表明的是溶洞系统向裂缝系统的窜流阶段，主要受到储容比及窜流系数的影响，储容比决定凹子的深浅及宽度，窜流系数决定凹子在压力导数曲线上的位置，同时也说明了流体在地层中窜流的能力大小。第3阶段为水平段：表明裂缝系统中流体产生径向流的时期，与裂缝的长度、宽度等参数有关。第4阶段为边界反映阶段：本文中所建立的模型的外边界条件为封闭边界，因此在压力及压力导数曲线的后期会出现上翘的现象，表明地层中整个系统都出现了径向流。

如图2所示的缝洞型碳酸盐岩油藏双孔单渗典型曲线，其各个流动阶段充分说明了缝洞型油藏中流体的渗流规律：井筒储集阶段，裂缝中流体向井底的窜流阶段，裂缝中流体的线性流阶段，溶洞中流体向裂缝的窜流阶段，以及整个地层的径向流阶段。根据缝洞型油藏的实际地质特征，充分说明了该模型对于研究缝洞型碳酸盐岩油藏中流体渗流特征及渗流机理的适用性。

3.2试井典型曲线敏感性分析

通过改变双孔单渗模型的参数值，可以计算出不同参数对应的定产生产井底压力数据，绘制无因次压力及压力导数的试井双对数曲线图，对试井典型曲线的敏感性进行进一步分析。

1）储容比对试井典型曲线的影响

在其他参数不变的情况下，通过改变储容比的值，计算不同值对应的井底压力，绘制试井双对数曲线，储容比对试井典型曲线的影响如图3所示。

从图3可以看出，储容比对压力及压力导数复合曲线的影响主要是中间部分的凹子，这也证明了以上分析的正确性：储容比决定了压力导数曲线中过渡段下凹的深度和宽度，随着储容比的减小，过渡段对应的凹子就会越宽且越深，说明过渡段时间越长，储容比越大，储容能力就越大。

2）窜流系数对试井典型曲線的影响

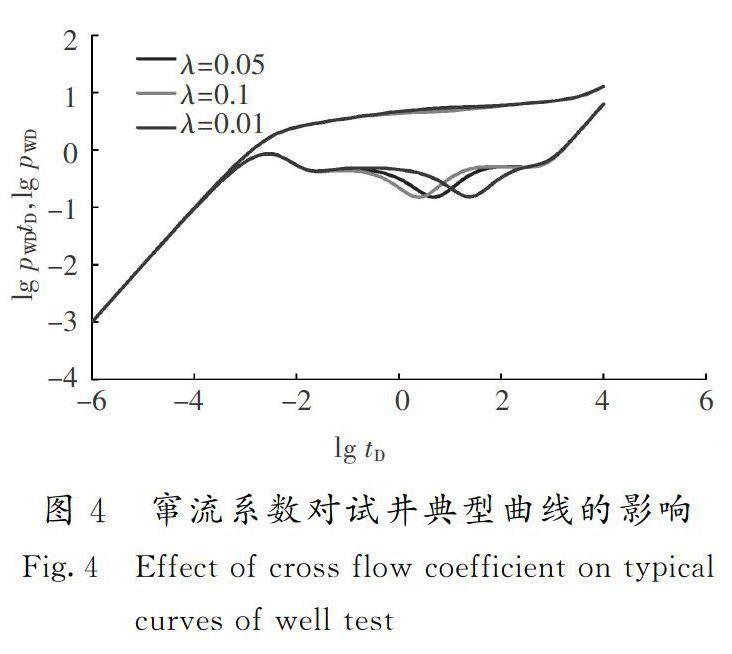
在其他参数不变的情况下，通过改变窜流系数的值，计算不同窜流系数的井底压力数据，利用不用时间下的井底压力及压力导数数据绘制试井双对数曲线。窜流系数对试井典型曲线的影响如图4所示。

分析图4可知，窜流系数对压力及压力导数曲线的影响如上述分析的一样，影响的是凹子的位置：随着窜流系数的减小，凹子就会越靠近右方，因为窜流系数反映的就是两种不同介质不同渗透率的比值以及岩石的几何结构，同时也反映了流体流动的性质。窜流系数越小，表明流体的窜流能力越小，流体的流动就会更加的困难，这就直接导致了整个地层系统进入径向流的时间推迟。

4结论

建立了考虑井筒储集和表皮系数的缝洞型碳酸盐岩油藏双孔单渗的试井物理模型及对应的数学模型，利用Laplace变换和Stehfest数值反演法算法对所建立的数学模型进行了求解，得到了不同时间的井底压力解。

1）利用模型的井底压力解绘制了试井典型曲线，并对试井典型曲线的特征及曲线的敏感性进行了分析。

2）表皮系数说明了流体流动阻力的大小，表皮系数越大，驼峰越陡峭，说明流体的流动阻力越大，地层周围的污染程度就越高。

3）储容比影响压力导数曲线中凹子的深度和宽度，储容比越小，凹子就越宽且越深，储容能力就越小。

4）窜流系数则决定了压力导数曲线中凹子的位置，窜流系数越小，说明流体的窜流能力越小，凹子也就越靠右方。

5）缝洞型油藏试井模型的建立要充分考虑到介质的非连续性，对于存在大尺度裂缝和溶洞的油藏，要考虑介质之间及介质与地层之间的窜流及压力的传递过程，对应到试井典型曲线上就是会出现明显的凹子，凹子的形状深浅主要是受到储容比和窜流系数的影响，因此缝洞型碳酸盐岩油藏试井时对于储容比和窜流系数的求解是非常重要的。

参考文献/References：

[1]POPOV P， QIN G， BI L， et al. Multi scale methods for modeling fluid flow through naturally fractured carbonate karsts reservoirs [C]//Spe Technical Conference and Exhibition.[S.l.]：[s.n.]，2009：218231.

[2]尹洪军， 张荣磊， 付春权， 等. 低渗透均质油藏不稳定渗流压力计算[J]. 特种油气藏， 2008， 15（5）： 5052.

YIN Hongjun， ZHANG Ronglei， FU Chunquan， et al. Transient pressure calculation for permeability homogeneous reservoirs [J]. Special Oil and Gas Reservoir， 2008， 15（5）： 5052.

[3]李红凯， 康志江. 碳酸盐岩缝洞型油藏溶蚀孔洞分类建模[J]. 特种油气藏， 2015， 22（5）： 5054.

LI Hongkai， KANG Zhijiang. Differential modeling of dissolved vugs in carbonate fracture and vug reservoirs [J]. Special Oil and Gas Reservoirs， 2015， 22（5）： 5054.

[4]熊伟， 常宝华， 潘懋， 等. 单井缝洞系统注水对含水率的影响分析[J]. 断块油气田， 2011， 8（4）： 479481.

XIONG Wei， CHANG Baohua， PAN Mao， et al. Impact of water injection on water content in single well fracturedvuggy system [J]. Fault Block Oil and Gas Filed， 2011， 8（4）： 479481.

[5]李阳. 塔河油田碳酸盐岩缝洞型油藏开发理论及方法[J]. 石油学报，2013， 22（1）： 115121.

LI Yang. The theory and method for development of carbonate fractured cavity reservoirs in Tahe oil field [J]. Acta Ptrolei Sinica， 2013， 22（1）： 115121.

[6]赵艳艳， 康志江， 张宏方. 单缝单洞缝洞型碳酸盐岩底水油藏弹性开采机理研究[J]. 西安石油大学学报（自然科学版）， 2013， 28（4）： 5154.

ZHAO Yanyan， KANG Zhijiang， ZHANG Hongfang. Study on the elastic production mechanism in fracturedvuggy carbonate reservoir of single fracture and single cave with bottom water [J]. Journal of Xian Shiyou University（Natural Science Edition）， 2013， 28（4）： 5154.

[7]雷刚， 张东晓， 杨伟， 等. 缝洞型油藏井钻遇大尺度部分充填溶洞数学模型[J]. 地球科学， 2017， 42（8）： 14131420.

LEI Gang， ZHANG Dongxiao， YANG Wei， et al. Mathematical model for wells drilled in largescale partially filled cavity in fracturedcavity reservoirs [J]. Earth Science， 2017， 42（8）： 14131420.

[8]薛承瑾， 戴卫华， 张皎生. 裂缝与井筒连通的三重介质油藏试井解释方法[J]. 油气地质与采收率， 2003， 10（3）： 3941.

XUE Chengjin， DAI Weihua， ZHANG Jiaosheng. Well test interpretation method for triple media oil reservoir in which fracture communicated with wellbore [J]. Petroleum Geology and Recovery Efficiency， 2003， 10（3）： 3941.

[9]常学军， 姚军， 戴卫华， 等. 裂缝和洞与井筒连通的三重介质油藏试井解释方法研究[J]. 水动力学研究与进展， 2004， 19（3）： 339346.

CHANG Xuejun， YAO Jun， DAI Weihua， et al. The study of well test interpretation method for a triple medium reservoir [J]. Journal of Hydrodynamics， 2004， 19（3）： 339346.

[10]王子胜， 姚军. 缝洞向井筒供液时三重压敏介质油藏压力响应特征研究[J]. 水动力学研究与进展， 2006， 21（1）：8489.

WANG Zisheng， YAO Jun. Study of pressure transient characteristic for stress sensitive triple medium reservoirs with fractures and vugs conveying fluids to wellbore [J]. Journal of Hydrodynamics， 2006， 21（1）： 8489.

[11]彭小龍， 杜志敏， 刘学利， 等. 大尺度溶洞裂缝型油藏试井新模型[J]. 西南石油大学学报（自然科学版）， 2008， 19（2）： 7477.

PENG Xiaolong， DU Zhimin， LIU Xueli， et al. A new well test model for the big size cavity fracture reservoirs [J]. Journal of Southwest Petroleum University， 2008， 19（2）： 7477.

[12]李江龙， 张冬丽， 吴玉树. 缝洞型油藏三重介质数值试井解释方法研究[J]. 水动力学研究与进展， 2012， 27（6）： 640648.

LI Jianglong， ZHANG Dongli， WU Yushu. Triplecontinuum numerical well test interpretation method for a naturally fractured vuggy reservoir [J]. Journal of Hydrodynamics， 2012， 27（6）： 640648.

[13]CAMACHO V R， VASQUEZ C M A， CASTREJONAIVAR R， et al. Pressure transient and decline curve behaviors in naturally fractured vuggy carbonate reservoirs [J]. SPE Reservoir Evaluation and Engineering， 2002， 8（2）： 95112.

[14]NELSON R A. Geologic Analysis of Naturally Fractured Reservoirs [M]. Houston： Goulf Publishing Company， 1985： 1822.

[15]陈俊昌， 朱宝峰， 鹿贞昆， 等. 塔中地区碳酸盐岩储层试井曲线类型研究[J]. 油气井测试， 2008， 17（2）： 2124.

CHEN Junchang， ZHU Baofeng， LU Zhenkun， et al. Study and application about type of testing curve for carbonate rock reservoir in middle tarim region [J]. Well Testing， 2008， 17（2）： 2124.

[16]譚承军， 吕景英， 李国蓉， 等. 塔河油田碳酸盐岩油藏产能特征与储集层类型的相关性[J]. 油气地质与采收率， 2001， 8（3）： 4345.

TAN Chengjun， LYU Jingying， LI Guorong， et al. Correlativity between productivity features and reservoir type in carbonate oil reservoirs of Tahe oilfield [J]. PGRE， 2001， 8（3）： 4345.

[17]康志江， 李江龙， 张冬丽， 等. 塔河缝洞型碳酸盐岩渗流特征[J]. 石油与天然气地质， 2005， 26（5）： 634640.

KANG Zhijiang， LI Jianglong， ZHANG Dongli， et al. Percolation characteristics of fractured vuggy carbonate reservoir in Tahe oilfield [J]. Oil and Gas Geology， 2005， 26（5）： 634640.

[18]马立平， 李允. 缝洞型油藏物质平衡方程计算方法研究[J]. 西南石油大学学报， 2007， 29（5）： 6668.

MA Liping， LI Yun. Calculation method of material equilibrium equation for fracture cave type reservoirs [J]. Journal of Southwest Petroleum University， 2007， 29（5）： 6668.

[19]彭小龙， 杜志敏， 刘学利， 等. 大尺度溶洞裂缝型油藏试井新模型[J]. 西南石油大学学报， 2008， 30（2）： 7477.

PENG Xiaolong， DU Zhimin， LIU Xueli， et al. A new well test model for the big size cavityfracture reservoirs[J].Journal of Southwest Petroleum University（Science and Technology Edition），2008，30（2）：7477.

[20]刘洪， 王新海， 任璐， 等. 含大尺度溶洞缝洞型油藏试井图版[J]. 特种油气藏， 2012， 19（2）： 7981.

LIU Hong， WANG Xinhai， REN Lu， et al. Pseudo threshold pressure gradient to flow for low permeability reservoirs [J]. Petroleum Exploration and Development， 2012， 19（2）： 7981.

[21]赵梓瑜， 尹洪军， 王磊. 垂直裂缝井椭圆流模型在F油田的应用[J]. 河北工业科技， 2017， 34（4）： 256269.

ZHAO Ziyu， YIN Hongjun， WANG Lei. Application of vertical fractured wells elliptical flow model in F oilfield[J]. Hebei Journal of Industrial Science and Technology， 2017， 34（4）： 256269.

[22]赵欢， 尹洪军， 李国庆， 等. “二三结合”开发模式渗流特征研究[J]. 河北科技大学学报， 2015， 36（4）： 437444.

ZHAO Huan， YIN Hongjun， LI Guoqing， et al. Seepage characteristics of the second tertiary combined model [J]. Journal of Hebei University of Science and Technology， 2015， 36（4）： 437444.