化学势在热力学与统计物理学中的作用

周小东,张云丽,孙现科

化学势最初是由吉布斯和路易斯引入的[1],在热力学与统计物理学中化学势是一个重要的物理量,且在热力学部分和统计物理学部分化学势的符号都用μ表示,但是在热力学和统计物理两个部分中化学势却有着不同的物理含义,这就造成对化学势物理含义的理解存在一定的困难.此外,符号μ还表示别的很多物理量,这更增加了学生学习的难度.因此为了使学生对化学势的物理含义更容易理解,就必要对化学势在热力学与统计物理中的物理概念、宏观和微观含义以及化学势的应用进行一个深入、系统地探讨.本文通过宏观和微观两种不同角度阐述化学势的物理含义,系统介绍了化学势在热力学与统计物理学中的具体应用,对化学势的物理含义有深入理解,从而突出化学势在热力学与统计物理学中的重要性.

1 化学势概念的引入

热力学系统准静态过程中,外界对系统所做的元功可以表示为:是外参量(广延量),Yi是与yi相应的广义力(强度量),W则为广义功.当多个外参量发生d yi变化时,外界对系统所做的功就等于各个外参量变化与相应广义力的乘积之和.

对于热力学气体系统,若只有气体体积发生改变,广义功表示为d W=-P d V(体积V为外参量,压强P为广义力),当外界对系统做正功时,系统外参量体积减小(-d V),此时广义功的物理含义表示为外界克服了系统内力做了功,则广义力压强(P)就表现为系统反抗气体体积减小的阻力.

对于一个静电场系统(带电量为q、电势为Φ),如果要向系统中增加电荷d q,需要克服电场力做功d W=Φd q(电量q为外参量,电势Φ为广义力),此时广义力电势Φ就反映出系统反抗电荷增加的阻力.

由上述两种广义力知,压缩体积需要克服压强做功,增加电荷需要克服电势做功,于是对于一个开放的热力学系统,增加粒子同样需要克服其他粒子反抗其增加的阻力.当外界使开放热力学系统粒子数增加d n时,外界对系统所做功可表示为d W=μd n,这里μ被定义为化学势,是一个强度量,此时广义力μ就反映系统反抗粒子数增加的能力.化学势μ的大小就反映了系统反抗粒子数增加的阻力的大小.此外,每种“势”都支配着与自己相关的能量和物质的迁移,如同电荷的迁移方向是由电势决定的,水的流动方向由重力势决定.对于热力学系统而言,当两相平衡未满足时,物质间的迁移方向就取决于其化学势的大小[2].

2 热力学中化学势的宏观含义

2.1 单元系中的化学势

对于单元系,系统的吉布斯函数表示为G T,P,n( )=nGmT,P( )是一个广延量,其中GmT,P( )为摩尔吉布斯函数.在这里引入化学势的概念就表示在温度(T)和压强(P)保持不变的情况下,每增加1 mol物质时所引起系统吉布斯函数的变化[3].即化学势可以表示为

通常在没有作特别说明时,化学势就是指偏摩尔吉布斯函数.吉布斯函数正是衡量对于等温等压的热力学系统体系变化的方向和平衡条件的一个标尺.

2.2 多元系中的化学势

多元系中,用ni来表示第i个组元的物质的量,则第i组元的化学势μi表示为在压强P、温度T和其他组元的物质的量nj不变的基础上,每增加1 mol的i组元物质,系统吉布斯函数的变化量[4].即:

对吉布斯函数G=G( T,P,n1,…,ni,…)求全微分可以得到:

由此式可知,吉布斯函数是以T,P,n1,…,ni,…为变量的特性函数.

又知U=G+TS-PV,对其求全微分并将上面(3)式代入,可得:

(4)式即是多元系的热力学基本方程.通过以上步骤,类似地可以求出自由能F和焓H的全微分表达式:

由(4)式以及F和H的全微分表达式可以知道,化学势μ也可以表为:

对于一个多组元的无限大系统中,在其他组元和外部情况不变的情况下,在一个特定环境中,每增加1mol物质,将引起系统性质的改变,如对于吉布斯函数G,它所表示的是在温度T、压强P和其他组元不变的情况下,每增加1 mol的i组元物质,此时化学势μ反映的是系统吉布斯函数G的变化情况;而对于系统的焓H,在熵S、压强P和其他组元不变的情况下,每增加1 mol的i组元物质时,这时化学势μ反映的是系统焓H的变化.因此,在不同的情况下,系统的化学势具有不同的物理含义.

3 化学势在热力学中的应用

3.1 理想气体中的化学势

在热力学中理想气体的物态方程为:

则1 mol理想气体的物态方程中n=1,则可知:pv=RT,μ=h-Ts(μ为摩尔吉布斯函数、h是摩尔焓,s是摩尔熵,v为摩尔体积).

以T、P为变量时,熵的全微分为

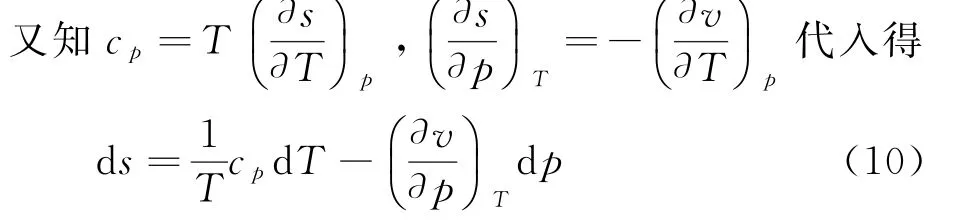
式中s1为积分常数.把(9)代入焓微分方程d h=T d s+v d p中得

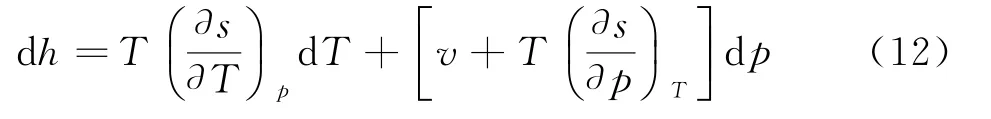
把cp和麦克斯韦关系式代入上式得

其中h1为积分常数.把(11)、(14)代入μ=h-Ts得

由上式知化学势是温度T和压强P的函数.方程中

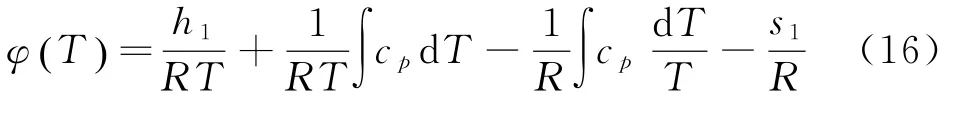
3.2 化学势在平衡相变中的应用

在单元复相系和多元复相系中,根据熵增加原理可以判断系统变化过程进行的方向,如等容等温下系统变化的方向是朝着吉布斯自由能减小的方向进行(ΔF≤0),而等温等压下系统是朝着吉布斯函数减小的方向进行(ΔG≤0).据此可推导出系统达到平衡时的判据条件是某元素在每一相中的化学势相等,即μαi=μβi,此为相变平衡条件.如果相变平衡未能满足,即μαi＞μβi变化将朝着δnα＜0的方向进行,也就是说,物质会从化学势高的相移动到化学势低的相去,这也就是μ被称为化学势的原因,其中:i表示系统中的某种元素,α、β表示系统中物质的相,n表示不同相的物质的量.

3.3 Clapeyron Equation的导出,源于化学势及其变化

根据相变平衡条件:

和相变平衡曲线(图1),分析气、液两相之间的关系,在图中所示,温度变化d T,并且使压强变化相应的d p,两相的化学势依旧是相等:

此时,两相中化学势增加量相等:

对化学势μ求其全微分:

即可推出Clapeyron Equation:

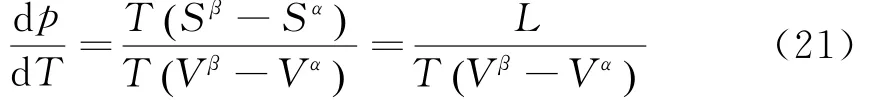
其中L=T( Sβ-Sα)表征1 mol物质由α相转变到β相时所吸收的相变潜热,因为相变时物质的温度不变.

图1 相变平衡曲线图

4 化学势在统计物理中的微观含义

4.1 统计物理中理想气体化学势的求解

理想气体的分布遵从玻耳兹曼统计[5],则单原子理想气体的配分函数为:

再由热力学量的统计表达式,就可以求出基本的热力学函数.吉布斯自由能F=U-TS是以T、V为变量的特性函数,其统计表达式为:

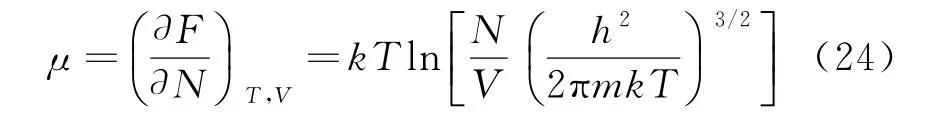
4.2 化学势在玻色—爱因斯坦凝聚现象中的应用

首先考虑一个由N个全同、近独立的波色子所组成的系统,温度为T、体积为V.由玻色分布可知,处于任意能级εl的粒子总数必大于零,即:(假设电子自旋为零).以ε0表示为粒子所能处的最低能级,则ε0＞μ,假设取最低能级是能级为零的点,即ε0=0,则此时化学势μ＜0,且化学势μ是由下式初始条件确定:

化学势μ是粒子数密度n和温度T的函数.εl,ωl和温度无关,在粒子密度n一定的情况下,化学势μ的升高会伴随着温度的降低,当温度下降到临界温度Tc时,μ将趋于0-,此时e-kTμc 趋于1.

临界温度Tc由下面方程确定:

T＞Tc时,μ为有限的负值,处在能级ε=0的粒子数很少,与系统中总的粒子数相比可忽略不计;T＜Tc时,μ趋于0-处在能级ε=0的粒子数却是不容忽略的数,因此T＜Tc时有:

第一项n0T()是T时刻位于能级ε=0的粒子数密度,第二项是位于能级ε＞0的粒子数密度nε＞0,积分得:

把(29)代入(28)得:

可见T＜Tc时,有可与n相近的粒子数在ε=0能级凝聚,称为玻色—爱因斯坦凝聚.由以上可见,需先有化学势μ判定出凝聚临界温度Tc后,才能进行后续物理量的计算,可知化学势在玻色—爱因斯坦凝聚中的重要作用[7].

4.3 费米电子气体中化学势的应用及物理含义

金属中的自由电子形成强简并的费米气体,由费米分布可知,温度为T时处在能级为ε上的一个量子态上的平均电子分布为[8]:

因为电子的自旋在它的动量上的投影在横轴与纵轴处有两个可能值,在气体体积V内,在范围内电子总量子态数是:

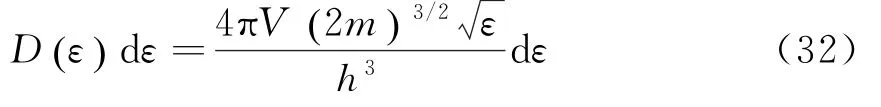
对于给定的电子数N、温度T和体积V,化学势可以通过下式确定:

由上面结果可知,μ是温度T与电子密度N/V的函数.

当T=0 K时,以μ0()表示电子气体在0 K时的化学势,由式(31)可知,0 K时费米气体的分布为[8]:

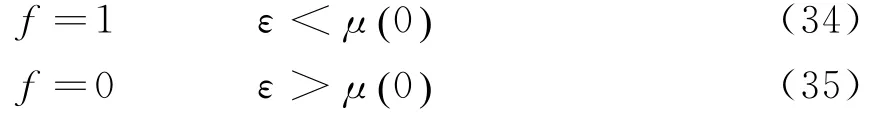
图2 T=0 K时电子气体分布函数图

如图2所示,(34)、(35)两式的意义在于,在T=0 K时,在ε＜μ0()的每一个量子态上的平均电子数为1,在ε＞μ0()的每一个量子态上的平均电子数为0.此分布可以理解为:在0 K时电子将尽可能的处于能量最低的状态,但泡利不相容原理则限制每一个量子态上最多只可以容纳一个电子,因此电子将从ε=0的状态逐渐填充至μ0()为止.

由分布可知,μ0()是0 K时电子的最大能量,可由下面步骤确定:

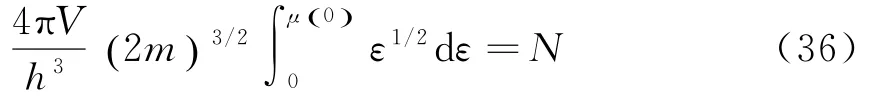
将上式积分,可得μ0()为:

pF是0 K时电子的最大动量,被称为费米动量.与它相应的速率v=被称为费米速率.在T=0 K时,电子气体的内能为:

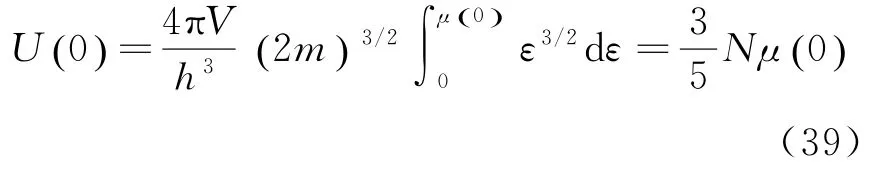
由以上式子可了解到,费米气体与理想玻色气体在T=0 K时粒子全部处于能量、动量、压强为0的状态完全不同,费米气体在T=0 K时依然具有很高的平均能量、动量,并产生很大的压强[8].

5 结论

在热力学与统计物理学中,化学势是非常重要的物理量之一,在热力学部分和统计物理部分化学势都起着非常重要的作用.本文由化学势概念的引入谈起,通过宏观和微观两种不同角度阐述化学势的物理含义,系统介绍了化学势在热力学和统计物理学中的具体应用,使我们对化学势的物理含义有更深入的理解,从而对热力学与统计物理学的学习和研究提供帮助.

参考文献:

[1]郭畅,张德生.关于化学势的讨论[J].安庆师范学院学报:自然科学版,2001,7(4):73-76.

[2]李良超,汤晓燕,王毅.热力学统计物理中化学势概念解析[J].西安邮电学院学报,2011,16(S2):127-128.

[3]王慧娟,韩光泽.化学势的普遍化表达式及其应用[J].华北电力大学学报,2012,39(1):109-112.

[4]廖碧涛,刘刚.热力学·统计物理中的化学势[J].绵阳师范学院学报,2008,27(2):132-133.

[5]尤良芳,董忠.热力学统计物理教材中几个问题的讨论[J].河西学院学报,2011,27(2):119.

[6]张宝金,张宁玉.热力学统计物理中的化学势[J].山东建筑工程学院学报,2005,20(4):91-92.

[7]马晴.热力学统计物理中化学势的计算[J].咸阳师范学院学报,2009,24(2):30-31.

[8]汪志诚.热力学·统计物理[M].4版.北京:高等教育出版社,2010:240-241.