试探方程法与Ostrovsky方程的精确解
郭汉东,张煜晨
在许多科学领域中,很多的问题最终可用非线性发展方程来描述,因此,寻求非线性发展方程的精确解成为了非线性领域中的热门课题之一.可由于非线性方程的复杂性,对于非线性方程还没有通用的解法.现在发展的新方法有齐次平衡法[1]、Jacobi椭圆函数法[2]、双曲正切函数展开法[3]等,它们各具特色.最近,刘成仕教授提出了新的求非线性发展方程精确行波解的方法,即试探方程法[4].其基本思想是把非线性发展方程约化为初等积分形式来求解.对于Ostrovsky方程[5],利用其他方法已求出了其许多精确解,本文则利用试探方程法给出Ostrovsky方程的新的精确行波解,丰富了其解的系统.
1 试探方程法
对于非线性偏微分方程

作行波变换

将式(2)代入式(1)整理可得非线性常微分方程


及u‴等其他导数项.将其代入式(3)中,得到u的多项式G(u),根据平衡原理确定m的值.令G(u)的系数都为零,得到一个非线性代数方程组,解方程组确定出a0,a1,…,am和d的值.
2 求1+1维Ostrovsky方程的精确解
这里求方程

的行波解,做行波变换

将式(6)代入式(5)中,化简整理可得

由试探方程步骤可知,假设u满足

将方程(8)两边同乘以u'积分一次并取积分常数为0,得
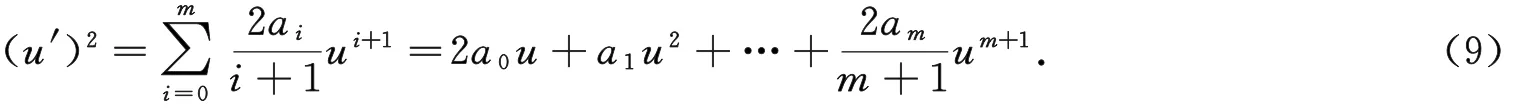
将方程(8)直接求导得

将式(8)(10)代入方程(7)得到

通过对上式整理,得

根据齐次平衡原则[6],得到m=2,那么,所取的试探方程为

这时,方程(11)就化简为

令u的各次项系数为0,得

由方程组(13),显然

其中A为任意常数.那么,方程(9)就化简为


当A≠0时,由式(16)可得[7]
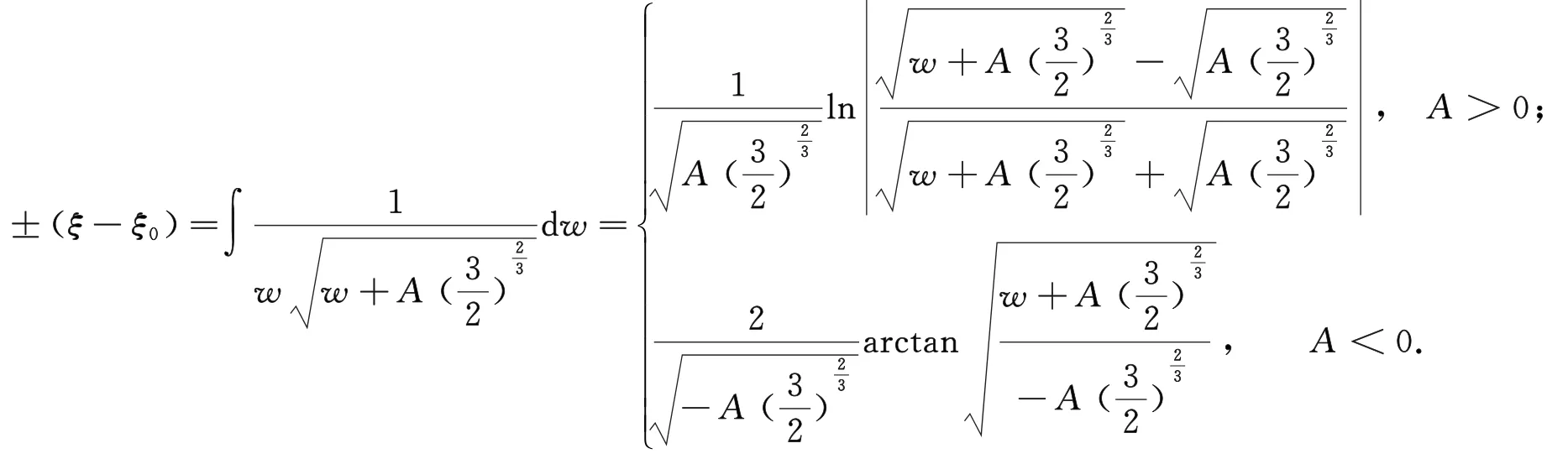
那么相应方程的解为

当A=0时,相应的方程的解为

3 结束语
利用试探方程法求解非线性偏微分方程的精确行波解,虽然得到的解不够全面,但是求解过程比较快捷、有效.随着对试探方程法的进一步研究,相信此方法的应用前景会更加广阔,并能有助于发现更多复杂的精确解.由于求解非线性偏微分方程精确行波解的方法各具特色,这种方法求出的精确行波解也是用其他方法而得不到的新解.
参考文献:
[1]范恩贵,张鸿庆.非线性孤子方程的齐次平衡法[J].物理学报,1998,47(3):353-362.
[2]刘式适.Jacobi椭圆函数展开法及其在求解非线性波动方程中的应用[J].物理学报,2001,50(11):2068-2073.
[3]Parkes E J,Duffy B R.Travelling solitary wave solutions to a compound Kd V-Burgers equation[J].Physics Letters A,1997,229:217-220.
[4]刘成仕.试探方程法及其在非线性发展方程中的应用[J].物理学报,2005,54(6):2505-2509.
[5]赵展辉,韩松,何晓莹.应用 (G'/G)-展开法求Ostrovsky方程的精确解[J].广西工学院学报,2012,23(1):74-81.
[6]王明亮,李志斌,周宇斌.齐次平衡原则及其应用[J].兰州大学学报:自然科学版,1999,35(3):8-15.
[7]杜兴华.非线性数学物理方程的精确解[M].哈尔滨:哈尔滨工程大学出版社,2010:11-12.

